旅行商问题的混沌混合离散蝙蝠算法
戚远航,蔡延光,蔡 颢,汤雅连,吕文祥
(1.广东工业大学自动化学院,广东广州510006;2.奥尔堡大学健康科学与技术系,丹麦奥尔堡9220)
旅行商问题的混沌混合离散蝙蝠算法
戚远航1,蔡延光1,蔡 颢2,汤雅连1,吕文祥1
(1.广东工业大学自动化学院,广东广州510006;2.奥尔堡大学健康科学与技术系,丹麦奥尔堡9220)
针对现有离散蝙蝠算法在求解旅行商问题时存在的收敛速度较慢、收敛率不高等问题,提出了混沌混合离散蝙蝠算法.该算法采用混沌初始化策略提高算法的寻优能力,引入2-Opt技术增强算法的局部搜索能力、加快算法的收敛速度.大量的仿真实验表明:所提出的算法在求解小规模TSP时能快速收敛到已知最优解;在求解大规模TSP时能在较短的时间内收敛到偏差0.4%以内的最优解.
旅行商问题;混沌初始化;蝙蝠算法;2-Opt
1 引言
旅行商问题(Traveling Salesman Problem,TSP)是组合优化中的一个著名难题.其求解算法很多,如遗传算法、蚁群算法、粒子群算法[1].
蝙蝠算法(Bat Algorithm,BA)是Xin-She YANG在2010年提出的一种元启发式算法[2].李枝勇等[3]提出了离散型蝙蝠算法求解最小比率旅行商问题,A Rezaee Jordehi[4]提出了混沌蝙蝠群算法.但是,现有离散蝙蝠算法在求解TSP时存在着收敛速度较慢、收敛率不高等问题.
本文提出了混沌混合离散蝙蝠算法(Chaotic Hybrid Discrete Bat Algorithm,CHDBA).CHDBA采用混沌初始化策略提高算法的寻优能力,引入2-Opt技术增强算法的局部搜索能力、加快算法的收敛速度.在大量的仿真实验中:与离散型蝙蝠算法[3](Discrete Bat Algorithm,DBA)、混合粒子群算法[5](Hybrid Particle Swarm Optimization,HPSO)相比,CHDBA在求解小规模TSP时能快速收敛到已知最优解;与混合遗传算法[6](Hybrid Genetic Algorithm,HGA)、离散型萤火虫群优化算法[7](Discrete Glowworm Swarm Optimization,DGSO)相比,CHDBA在求解大规模TSP时能在较短的时间内收敛到偏差0.4%以内的最优解.
2 TSP的定义及其数学模型
给定n个城市以及各城市之间的距离,要求找到一条遍历所有城市且每个城市只能被访问一次的路径,并使得总路径长度最短.数学模型[8]:对于n个城市,遍历所有城市且只能被访问一次的路径为C=(c1,c2,…,cn),使
(1)
其中,d(ci,ci+1)为城市ci、ci+1之间的距离,i=1,2,…,n-1,d(cn,c1)为cn、c1之间的距离.
3 混沌混合离散蝙蝠算法
3.1 参数定义与算子设计
①蝙蝠位置:第i个蝙蝠的位置定义为xi=(xi1,xi2,…,xin),其中n为城市的个数,i=1,2,…,Q(Q∈N+为种群规模),(xi1,xi2,…,xin)是(1,2,…,n)的一个置换.xi表示第i个蝙蝠的城市遍历路径为xi1→xi2→…→xin→xi1.
②蝙蝠速度:第i个蝙蝠的速度定义为vi={(si1,ti1),(si2,ti2),…,(sin,tin)},其中sim,tim∈{1,2,…,n},m=1,2,…,n.
③蝙蝠频率:第i个蝙蝠的频率定义为fi∈[0,1].
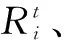
(2)
(3)
其中:α、γ均为常数,0<α<1、γ>0;t=1,2,….
⑤置换操作:设第i个蝙蝠的位置为xi=(xi1,xi2,…,xin),wi=(k1,k2)为置换序列,其中k1,k2=1,2,…,n.xi的基于wi的置换操作是指xi中第k1分量和第k2分量互换位置.
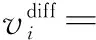
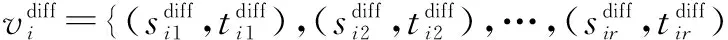

3.2 混沌初始化
3.2.1 Logistic映射
选用Logistic映射来产生混沌序列:
zi+1=μzi(1-zi)
(4)
其中0≤zi≤1且zi≠0.25,0.5,0.75,i=0,1,2,…,μ=4.
3.2.2 混沌量与路径的对应关系
应用全排列构造理论[9]建立序号D(D∈{1,…,n!})与路径(即1,2,…,n的全排列)的对应关系.
以(1,2,3)的全排列为例,序号D、向量V和构造C(即路径)组成了DVC表,如表1所示.

表1 (1,2,3)全排列的DVC表
①D/V转换公式:
(5)
其中i=1,2,…,n-1.
以(1,2,3)的全排列为例,n=3;取序号D=3,根据式(5)可得V=(v1,v2)=(2,2).
②V/C转换
通过向量V的指针功能来确定构造C.
以V=(2,2)为例,转换步骤如表2所示.

表1 V/C转换步骤
从表2可看出,C=(c1,c2,c3)=(2,3,1).
③混沌量可以与向量V的转换公式
由式(4)产生混沌量zi,则D0=n!zi,代入式(5),令d1=nzi,得
(6)
其中i=2,3,…,n-1.
混沌量zi与向量V对应,再通过V/C转换,混沌量zi便可与构造C(即路径)对应.
3.2.3 混沌初始化策略
当蝙蝠种群初始化时,通过式(4)和式(6)生成一定数量的可选择的蝙蝠位置,择优初始化蝙蝠种群,以此加快算法的收敛速度.
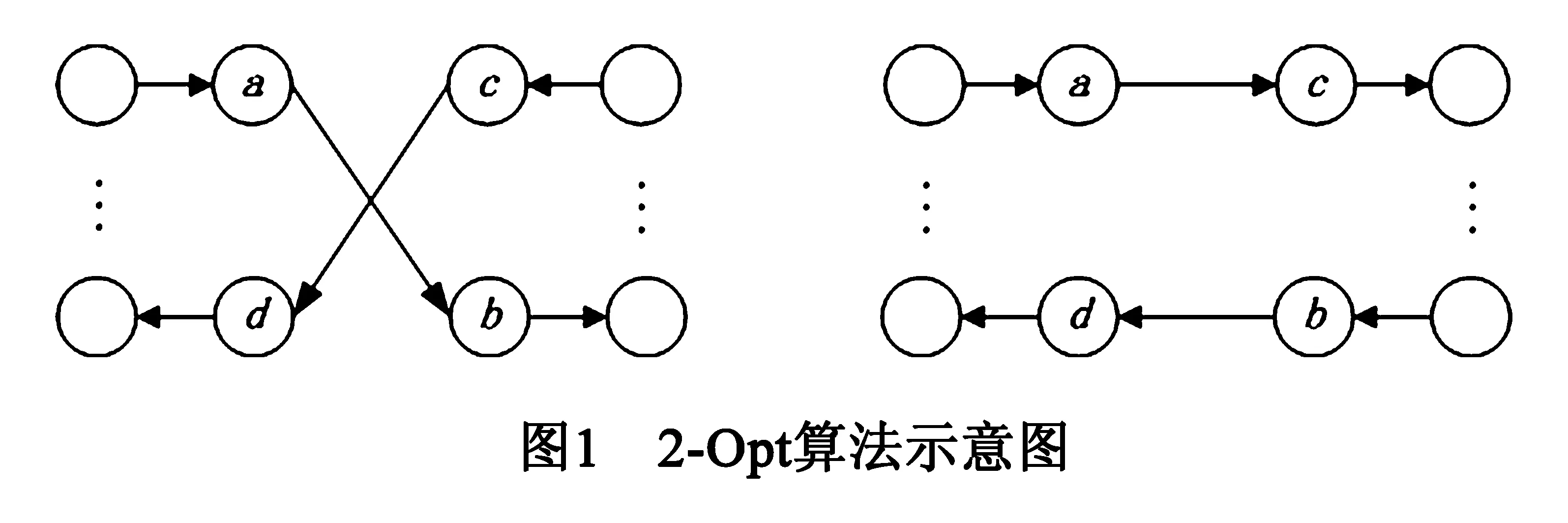
3.3 2-Opt算法
2-Opt算法示意图如图1所示,其中没有标号的顶点代表两个或者两个以上顶点间一系列的边.如果ab+cd>ac+bd成立,则删除边ab和cd,同时增加边ac和bd,并把顶点b、c之间的边反向[10].
3.4 算法步骤

第2步:根据初始蝙蝠种群中每个蝙蝠的xi计算函数适应值fitnessi,初始化全局最优解x*和fitness*.
第8步:如果Nnow 第9步:输出全局最优解x*. 4.1 实验环境与算法参数设置 实验软件为VS2008,CPU为Intel Core i7 2.30GHz,内存为4GB,Window 7操作系统. 在仿真实验的分析中,收敛率、偏差分别由式(7)、(8)定义,“已知最优解”是指TSPLIB标准库提供的最优解,“——”是指所参考的文献并未提供该相关数据. 收敛率 (7) 偏差 (8) 表3 CHDBA在不同TSP算例中种群规模和最大迭代次数的取值 4.2 小规模TSP实验与分析 小规模TSP实验中,将CHDBA和DBA、HPSO进行比较,实验结果如表4所示. 从表4可以看出,针对小规模TSP,CHDBA具有较好的寻优能力(所有算例均收敛到已知最优解),偏差为0,收敛率为100%,较少的时间耗费.图2(a)为CHDBA优化Eil51的最优解. 表4 小规模TSP实验结果 4.3 大规模TSP实验与分析 大规模TSP实验中,将CHDBA和HGA、DGSO进行比较,实验结果如表5所示. 从表5可以看出,针对大规模TSP,CHDBA能收敛到偏差0.4%以内的最优解,寻优能力比DGSO、HGA更强,而相对于HGA,CHDBA耗费的时间更少.尤其在Krob200中,CHDBA虽然也没有收敛到已知最优解,但是收敛结果为29554.13,偏差仅为0.39%,比DGSO降低了0.18%,比HGA降低了0.02%,耗费的时间却仅为HGA的1/4.图2(b)、2(c)、2(d)分别为CHDBA优化Ch130、Krob150和Krob200的最优解. 表5 大规模TSP实验结果 本文提出的CHDBA采用混沌初始化策略提高算法的寻优能力,引入2-Opt技术增强算法的局部搜索能力、加快算法的收敛速度.大量的仿真实验表明:CHDBA在求解小规模TSP时能快速收敛到已知最优解,在求解大规模TSP时能在较短的时间内收敛到偏差0.4%以内的最优解.今后工作仍需进行更多的数值实验和对算法的参数取值做进一步的研究. [1]高海昌,冯博琴,朱利.智能优化算法求解TSP问题[J].控制与决策,2006,21(3):241-247. GAO Hai-chang,FENG Bo-qin,ZHU Li.Reviews of the meta-heuristic algorithms for TSP [J].Control and Decision,2006,21(3):241-247.(in Chinese) [2]Xin-She YANG.A new metaheuristic bat-inspired algorithm [J].Nature Inspired Cooperative Strategies for Optimization,2010,284:65-74. [3]李枝勇,马良,张慧珍.求解最小比率旅行商问题的离散蝙蝠算法[J].计算机应用研究,2015,32(2):356-359. LI Zhi-yong,MA Liang,ZHANG Hui-zhen.Discretebat algorithm for solving minimum ratio traveling salesman problem [J].Application Research of Computers,2015,32(2):356-359.(in Chinese) [4]A Rezaee Jordehi.Chaotic bat swarm optimization (CBSO) [J].Applied Soft Computing,2015,26:523-530. [5]俞靓亮,王万良,介婧.基于混合粒子群优化算法的旅行商问题求解[J].计算机工程,2010,36(11):183-184. YU Liang-liang,WANG Wan-liang,JIE Jing.Solution of travel salesman problem based on hybrid particle swarm optimization algorithm [J].Computer Engineering,2010,36(11):183-184.(in Chinese) [6]Yong Wang.The hybrid genetic algorithm with two local optimization strategies for traveling salesman problem [J].Computers & Industrial Engineering,2014,70:124-133. [7]周永权,黄正新,刘洪霞.求解TSP问题的离散型萤火虫群优化算法[J].电子学报,2012,40(6):1164-1170. ZHOU Yong-quan,HUANG Zheng-xin,LIU Hong-xia.Discrete glowworm swarm optimization algorithm for TSP problem [J].Acta Electronica Sinica,2012,40(6):1164-1170.(in Chinese) [8]Marjan Kuchaki Rafsanjani,Sadegh Eskandari,Arsham Borumand Saeid.A similarity-based mechanism to control genetic algorithm and local search hybridization to solve traveling salesman problem [J].Neural Computing and Applications,2015,26(1):213-222. [9]高尚.解旅行商问题的混沌蚁群算法[J].系统工程理论与实践,2005,25(9):100-104. GAO Shang.Solving traveling salesman problem by chaos ant colony optimization algorithm [J].System Engineering Theory and Practice,2005,25(9):100-104.(in Chinese) [10]姜昌华,戴树贵,胡幼华.求解车辆路径问题的混合遗传算法[J].计算机集成制造系统,2007,13(10):2047-2052. JIANG Chang-hua,DAI Shu-gui,HU You-hua.Hybrid genetic algorithm for capacitated vehicle routing problem [J].Computer Integrated Manufacturing Systems,2007,13(10):2047-2052.(in Chinese) 戚远航 男,1993年6月出生,广东湛江人.现为广东工业大学硕博连读生,从事供应链物流及智能算法的研究. E-mail:qiyuanhang77@163.com 蔡延光 男,1963年2月出生,湖北咸宁人.1988年和1996年分别在重庆大学和浙江大学获理学硕士和工学博士学位.现为广东工业大学教授,博士生导师,从事复杂网络系统建模、控制与优化、物流控制与优化、智能交通系统、组合优化、智能优化、物联网信息处理与优化控制等方面的研究. Chaotic Hybrid Discrete Bat Algorithm for Traveling Salesman Problem QI Yuan-hang1,CAI Yan-guang1,CAI Hao2,TANG Ya-lian1,LÜ Wen-xiang1 (1.SchoolofAutomation,GuangdongUniversityofTechnology,Guangzhou,Guangdong510006,China;2.DepartmentofHealthScience&Technology,AalborgUniversity,Aalborg9220,Denmark) In view of some problems,like slow convergence speed and low constringency rate,arising during the process of applying discrete bat algorithms to solve travelling salesman problem,a chaotic hybrid discrete bat algorithm is proposed.The proposed algorithm adopts chaotic initialization strategy to improve the capability of optimization,and the 2-Opt to enhance the capability of local search and to speed up the convergence speed.A large amount of simulations show that the algorithm can achieve their solutions rapidly for some small scale traveling salesman problems,and obtain their solutions in a relatively short time with the error less than 0.4% for large ones. traveling salesman problem;chaotic initialization;bat algorithm;2-Opt 2015-03-24; 2015-06-04;责任编辑:李勇锋 国家自然科学基金(No.61074147);广东省自然科学基金(No.S2011010005059);广东省教育部产学研结合项目(No.2012B091000171,No.2011B090400460);广东省科技计划项目(No.2012B050600028,No.2014B010118004);广州市花都区科技计划项目(No.HD14ZD001) TP301 A 0372-2112 (2016)10-2543-05 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.10.0374 算法测试


5 结语



