基于加权非负矩阵分解的链接预测算法

王萌萌,左万利,王 英

(1.吉林大学计算机科学与技术学院,吉林长春 130012; 2.符号计算与知识工程教育部重点实验室(吉林大学),吉林长春 130012)



基于加权非负矩阵分解的链接预测算法

王萌萌1,2,左万利1,2,王 英1,2

(1.吉林大学计算机科学与技术学院,吉林长春 130012; 2.符号计算与知识工程教育部重点实验室(吉林大学),吉林长春 130012)

本文针对在线微博，首先，基于带权动态链接预测特征集合，以用户社会关系因子约束目标函数，从用户概要和用户发布内容两个维度利用非负矩阵分解方法预测社会网络中链接的存在性和方向性.然后，在真实的数据集上验证了提出框架的有效性，并通过实验进一步证明了特征权重和时间信息在链接预测问题中的重要性.

有向链接预测;非负矩阵分解;特征权重;时间信息;动态社会网络

1 引言

随着社会媒体的普及，每天有大量的用户通过网络中的关系结构彼此交互并影响.作为关系结构分析中的基础问题，链接预测近年来受到了越来越多的关注，其不但能够分析社会网络中的缺失数据，还可被应用到分子生物学[1]、犯罪调查[2]、信息检索[3]和推荐系统[4]等领域.此外，其还有助于深入理解社会网络的演化机理.综上，除广阔的应用前景外，链接预测还具有重要的理论意义，然而，传统算法并不能对动态社会网络中的有向链接进行预测，因此，本文提出了一种基于加权非负矩阵分解的链接预测模型(Weighted Nonnegative Matrix Factorization Model for Link Prediction，WNMFLP)，主要贡献如下.

(1)根据链接预测特征与类别间的相关性量化特征的重要性，构建带权特征集合.

(2)基于用户网络结构信息和发布内容信息的时间序列构建动态链接预测特征，以刻画网络结构与信息的动态演变过程.

(3)利用用户社会关系因子约束目标函数，将预测问题转化为求解用户概要和用户发布内容两个维度的加权非负矩阵分解最优解问题，有效降低了时间复杂性且使其能够准确预测链接的存在性与方向性.

2 相关工作

近几年，社会网络中的链接预测问题吸引了国内外众多学者，学者们研究并利用不同的数学方法构建链接预测模型，大大推动了链接预测建模理论的发展[5～8].

由于仅基于拓扑结构特征的链接预测方法较为简单，所以一些学者对拓扑结构特征计算方法进行了改进：Schall[9]提出了一种基于三元闭合关系的拓扑结构特征，通过图模式对节点间的链接进行预测，并在真实数据集上验证了提出方法的有效性，其为社会网络中有向链接的预测问题提供了一种新思路.Symeonidis等人[10]基于从Laplacian矩阵特征向量中获取的信息，通过多路谱聚类方法对节点进行社区划分，并利用正链接和负链接的信息计算节点间的拓扑结构特征，从而实现链接的预测.Fire等人[11]首先基于链接方向定义了一组拓扑结构特征，然后利用J48决策树、Bagging和随机森林方法在真实的数据集上进行链接预测取得了较好的实验结果.

还有一些学者通过融合更多类型的信息对链接预测算法进行改进：Lou等人[12]基于地理距离和网络同构性对用户链接关系的影响，提出了一种预测Twitter中节点间社会关系的学习模型.Jorge和Alneu[13]首先应用社区检测算法为节点划分社区标签，然后基于社区信息和局部信息，分别通过监督和非监督的学习方法对网络中的链接进行预测，该方法首次在链接预测方法中融入了社区信息.

此外，一些研究者通过引入时间信息对链接预测算法进行改进：Soares和Prudêncio[14]基于非链接节点对间邻近度分数的时间序列，分别通过监督和非监督学习方法对节点间的链接进行预测，并在其基础上提出了一种基于时间事件的邻近度度量方法[15]，其能够较好地表示动态变化的网络结构，并准确地预测节点间的链接.Zhang等人[16]基于朋友关系的传递性，将以一个节点为中心的朋友网络的增长过程表示成树状结构，除根节点外，树中每个结点的位置由其与根节点建立朋友关系的时间决定，为链接预测模型构建提供了一个新视角.

综上，在动态社会网络有向链接预测的研究中，如何刻画链接的方向性和网络的动态性、量化不同特征的重要性以及构建模型仍是非常具有挑战性的工作.

3 动态链接预测特征建模

3.1 动态链接预测特征定义

3.1.1 用户概要特征

本文将原始数据集[17]中的特征直接作为用户概要特征，其中具有离散属性的特征以不同的数值表示其所属类别.

3.1.2 用户动态关系特征

由于用户在网络中的地位越相近，其拓扑结构越相似[18]，故其间越易建立联系.根据社会网络的动态性，本文将网络看作一个时间片流(一个时间片表示一天且一个时间片越久，其重要性越低，权重越小).由于传统的拓扑度量未考虑链接的方向性，因此，首先拟基于链接的方向性对几种传统的度量方法进行改进.

(1)改进的Salton度量标准

Common Neighbors度量标准假设两个用户间的相似度与其拥有的共同邻居数量成正比，Salton度量标准在其基础上加入了两个用户的度信息.基于链接的方向性对其改进后，用户和用户在第个时间片上的Salton值为：

Sa(u,v,ti)=

(1)

其中，Γin(u,ti)和Γin(v,ti)分别为u和v在ti上的入链接用户集合；Γout(u,ti)和Γout(v,ti)分别为u和v在ti上的出链接用户集合；入链接和出链接由用户间的关注关系决定；|·|为集合的元素数量.则在时间片流[0,tn]上，u和v的Salton值为：

(2)

其中，β∈[0,1]，βn-i为ti的权重，n为[0,tn]上的时间片总数.

(2)改进的Jaccard度量标准

Jaccard度量标准假设两个用户间的相似度正比于其拥有的共同邻居数量与其所有邻居数量的比值.基于链接的方向性对其改进后，u和v在ti上的Jaccard值为：

Ja(u,v,ti)

(3)

本文以与式(2)中相同的βn-i表示ti的权重，则u和v在[0,tn]上的Jaccard值为：

(4)

(3)改进的Preferential Attachment度量标准

Preferential Attachment度量标准假设用户的度越大，该用户与其他用户建立链接的可能性就越大.基于链接的方向性对其改进后，u和v在ti上的Preferential Attachment值为：

(5)

本文以与式(2)中相同的βn-i表示ti的权重，则u和v在[0,tn]上的Preferential Attachment值为：

(6)

3.1.3 用户动态发布内容特征

有时，情感的“共鸣”使得用户间更易建立联系：若用户A最近总是发布一些消极的状态，而用户B最近总是发布一些积极的状态，则A很有可能建立指向B的链接，进而从B发布的状态中汲取正能量以平复自己低落的心情.因此，拟利用知网英文情感分析用词语集(http://www.keenage.com/download/sentiment.rar)，基于用户发布的文本信息计算用户u在ti上的发布内容特征：

Em(u,ti)=pn(u,ti)/nn(u,ti)

(7)

其中，pn(u,ti)和nn(u,ti)为u在ti上发表的微博文本集合中使用的包含在上述词语集中的正向情感词数和负向情感词数.以与式(2)中相同的βn-i表示ti的权重，则在[0,tn]上，u的动态发布内容特征为：

(8)

3.2 动态链接预测特征权重分配

由于在链接预测问题中不同特征重要性不同，故为其合理分配权重就显得尤为重要.肯德尔检验是一种通过计算相关系数测试两个随机变量的统计依赖性的非参数假设检验，因此，拟通过计算链接预测特征与类别间的肯德尔相关系数量化特征的重要性，随机变量X和Y间的肯德尔相关系数为：

(9)

其中，τ(X,Y)∈[-1,1]，τ(X,Y)为1、-1和0时分别表示X和Y的等级相关性一致、不一致和相互独立.C和D分别为和中拥有一致性和不一致性的元素对数；N为随机变量的维数；N1和N2分别为X和Y中重复元素的总数，以N1为例，其计算如下：

(10)

其中，s为拥有相同元素的元素数量；Ui为第i个元素拥有相同元素的数量；则特征i的权重其计算如下：

(11)

其中，ωi为特征i的权重，L∈{1,-1,0}表示链接类别，下一节中会对其进行详细定义，τ(i,L)为特征i与L间的肯德尔相关系数；m为特征维数.

4 基于加权非负矩阵分解的链接预测模型

4.1 问题定义

文献[19]中指出因为纯加性和稀疏的描述能使对数据的解释变得合理，还因为相对稀疏性的表示方式能在一定程度上抑制由外界变化给特征提取带来的不利影响，所以非负矩阵分解方法已逐渐成为一种有效的多维数据处理工具.由于用户链接矩阵是低秩且稀疏的，因此，拟将动态网络中有向链接的预测问题转化为求解非负矩阵分解的最优解问题.令u={u1,u2,…,um}表示用户集合，m表示用户数量；R∈m×m表示用户-用户矩阵，其中，假设ui到ui不存在链接，即；Rii=0;ui和uj(i≠j)间的链接预测结果可为：链接由ui指向uj(Rij=1)；链接由uj指向ui(Rij=-1)；ui与uj间无链接(Rij=0)，则本文将动态社会网络中的有向链接预测问题定义为：给定用户转发矩阵R和用户-特征矩阵U1，找到非负矩阵V1，使其满足R≈UiVi，从而获得链接关系预测矩阵R′=U1V1.

4.2 模型算法

首先，将R分解为矩阵U1∈m×d1和矩阵V1∈m×d1，其中，d1≪m为用户概要特征和用户动态发布内容特征的总数，V1为R与U1低秩表示间的关系.然后，最小化预测值与实际值间的均方误差，并加入U1和V1的正则化Frobenius范数以避免发生过拟合：

(12)

其中，||·||F为Frobenius范数；λ1和λ2为正则化参数.假设社会关系相似的用户间用户概要差异较小，因此，为约束用户间用户概要的差异，定义正则化的用户社会关系因子为：

(13)

其中，S[0,tn](i,j)∈[0,1]为ui和uj间在[0,tn]上的社会关系因子，S[0,tn](i,j)越大，ui和uj间越可能建立链接，则用户间Frobenius范数越小，ui和uj间在[0,tn]上的社会关系因子为：

S[0,tn](i,j) =ωSa·Sa[0,tn](i,j)+ωJa·Ja[0,tn](i,j)

+ωPa·Pa[0,tn](i,j)

(14)

其中，(U1)i*和(U1)j*分别为ui和uj的特征集合；Tr(·)为矩阵的迹；L=D-S[0,tn]为拉普拉斯矩阵，D为对角矩阵，D中的第i个元素D(i,i)为S[0,tn]中第行元素之和.则加入正则化社会因子的目标函数为：

(15)

虽然较难形式化F1的全局最优解，但F1的局部最优解可以通过乘性迭代方法求得[20].为计算U1和V1的更新规则，去掉式(15)中的常数，其拉格朗日函数为：

-Tr(ψU1)-Tr(φV1)

(16)

其中，ψ和φ分别是U1和V1的非负拉格朗日乘子.然后，分别计算式(16)中关于U1和V1的梯度，并设其为0：

(17)

在式(17)两边分别乘以U1和V1：

(18)

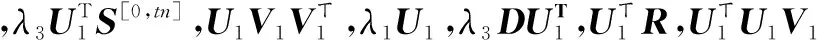
(19)

则基于加权非负矩阵分解的链接预测模型如算法1所示.

算法1 基于加权非负矩阵分解的链接预测模型

输入:用户转发矩阵R用户-特征矩阵U1；用户社会关系因子矩阵S[0,tn]；正则化参数λ1，λ2，λ3

输出:链接关系预测矩阵R′

1:For U1中的每一列gDo

2: 根据式(11)计算相应特征权重ωg

3: 以ωg乘以列g中元素，得到带权的特征值

4:End for

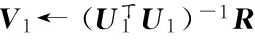
6:Repeat

7: 根据式(19)更新U1和V1

8:Until 式(15)中的F1收敛

9:Return R′ ← U1V1

4.3 时间复杂度分析

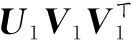
5 实验及结果分析

5.1 数据集及实验设置

本文选用文献[17]中的数据集验证提出方法的有效性，该数据集中收集了从2012年9月28日到10月29日的新浪微博网络结构信息，其统计数据如表1所示.

表1 新浪微博数据集统计数据

则实验设置如下：随机将数据集分为两部分——A和B.A为训练集合，占数据集的90%；余下的10%记作B，作为测试集合.为确保实验结果的可靠性，本文采用10折交叉验证利用准确率，召回率和F1值对实验结果进行评估.

5.2 对比实验

5.2.1 WNMFLP与其他链接预测方法的比较

本文基于新浪微博数据集将提出的o-WNMFLP与f-J48、f-Bagging、f-RF、o-J48、o-Bagging、o-RF和s-GM进行对比，其中，f、s和o分别表示文献[11]、文献[9]和本文中定义的特征；J48、Bagging、RF和GM分别表示J48决策树、Bagging、随机森林和图模式方法.由于图模型并不适用于本文提出的特征，因此，本文仅与s-GM进行对比.图1和图2中分别为每一种方法的平均F1值和平均执行时间(以秒为单位).

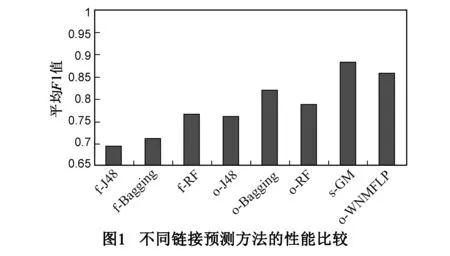
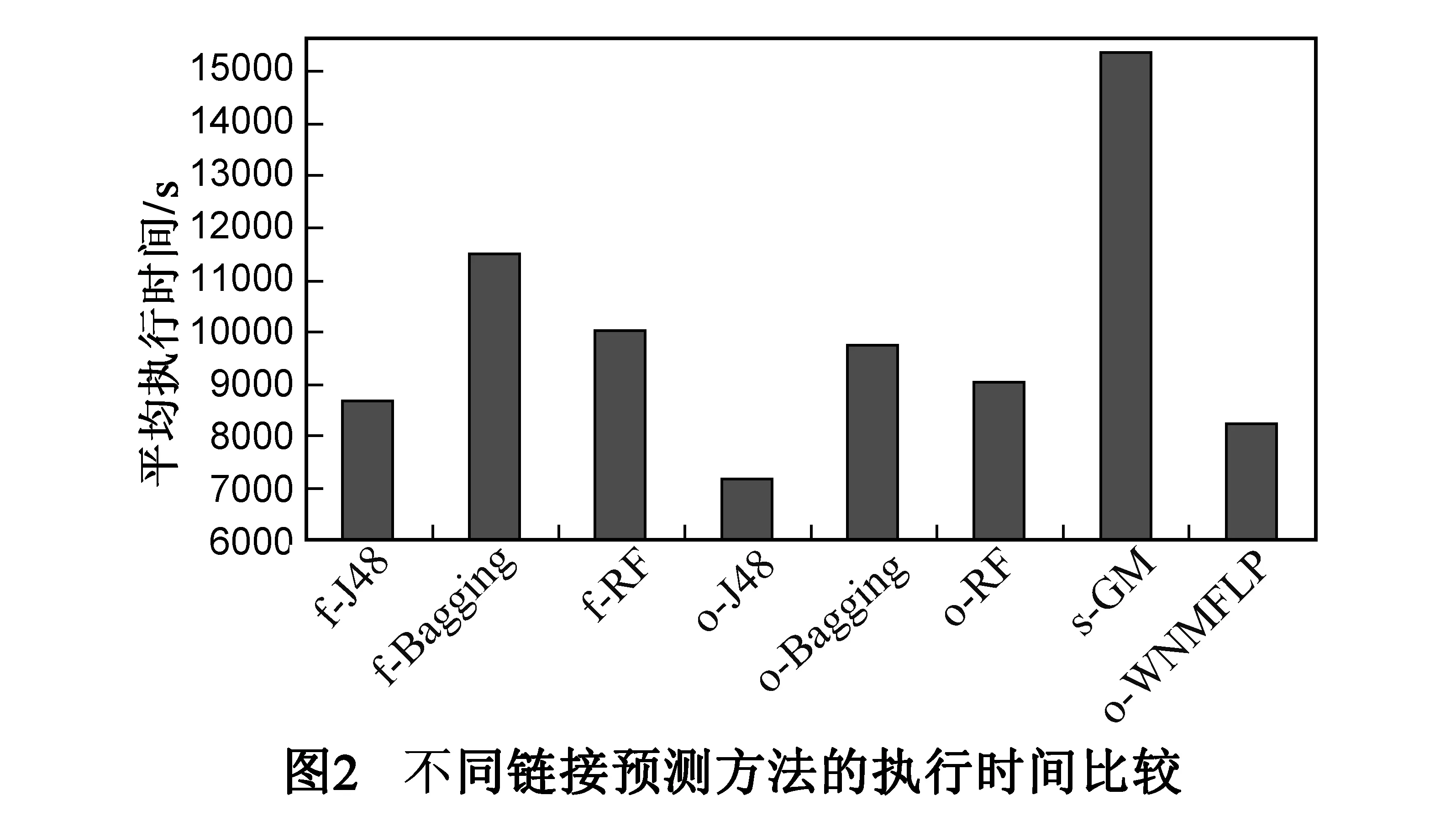
通过图1和图2可知，当基于相同特征集合时，本文提出的方法与o-J48、o-Bagging、o-RF相比，其平均F1值分别能够提升9.6%、3.9%和6.9%：J48决策树的执行时间最短，但是由于决策树构建时信息增益的结果偏向于那些具有更多数值的特征，故在本文的数据集上平均F1值最低；随机森林作为一种集成的决策树，其通过随机选择特征集合的一个子集构建决策树，进而避免了在特征数量较多时出现过度拟合现象；Bagging和随机森林的平均F1值差别不大，但其执行时间较长；与其他方法相比，通过将预测问题转化为求解加权非负矩阵分解问题，WNMFLP可以在相对较短的执行时间内获得相对较高的平均F1值.当基于不同特征集合时，本文提出的特征集合与文献[11]中提出的特征集合相比，在J48决策树、Bagging和随机森林方法上的平均F1值分别能够提升6.7%、10.7%和2.2%，由此可见，本文提出的动态特征能够以更高的精度预测链接的存在性和方向性.最后，仅基于相同的数据集，尽管o-WNMFLP的平均F1值略低于s-GM(-2.4%)，但相比于s-GM，o-WNMFLP大大缩短了链接预测的执行时间(-46.9%).

综上，相比于其他特征定义和链接预测方法，本文提出的方法使得链接预测算法的综合性能得到了较大提升.

5.2.2 特征权重对WNMFLP性能的影响

表2为各特征的权重平均值.

通过表2可知，用户动态发布内容特征的权重平均值高于用户动态关系特征，用户概要特征中，城市、账户创建时间和账户认证类型的权重平均值高于用户动态发布内容特征.

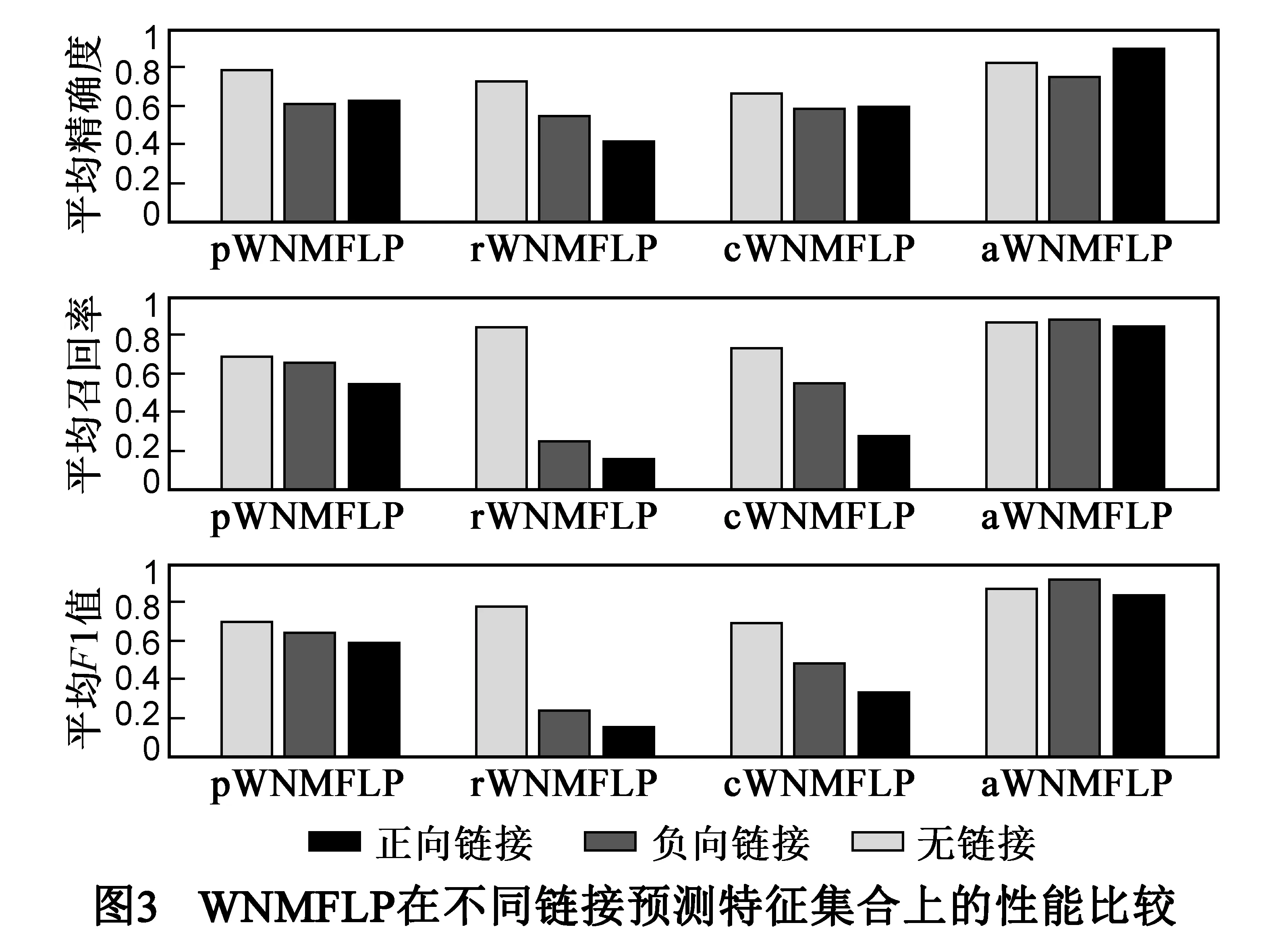
图3为WNMFLP在不同特征集合上的性能比较，其中，p、r、c和a分别表示用户概要特征、用户动态关系特征、用户动态发布内容特征和所有特征.

图3中的实验结果也表明，pWNMFLP的精确度总体上高于cWNMFLP和rWNMFLP；就链接的方向性预测而言，cWNMFLP的精确度高于rWNMFLP；就链接的存在性预测而言，rWNMFLP的精确度高于cWNMFLP.

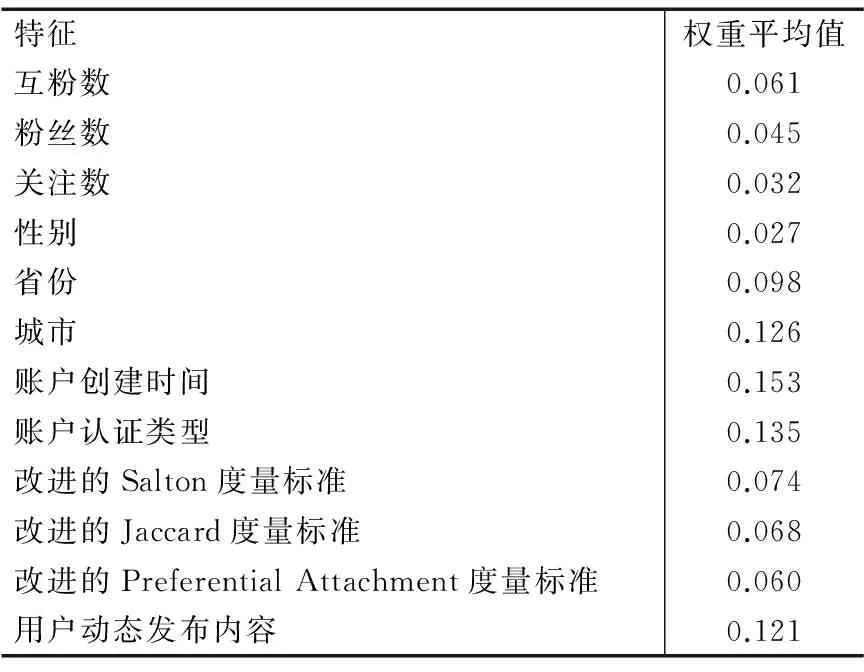
表2 各特征权重平均值

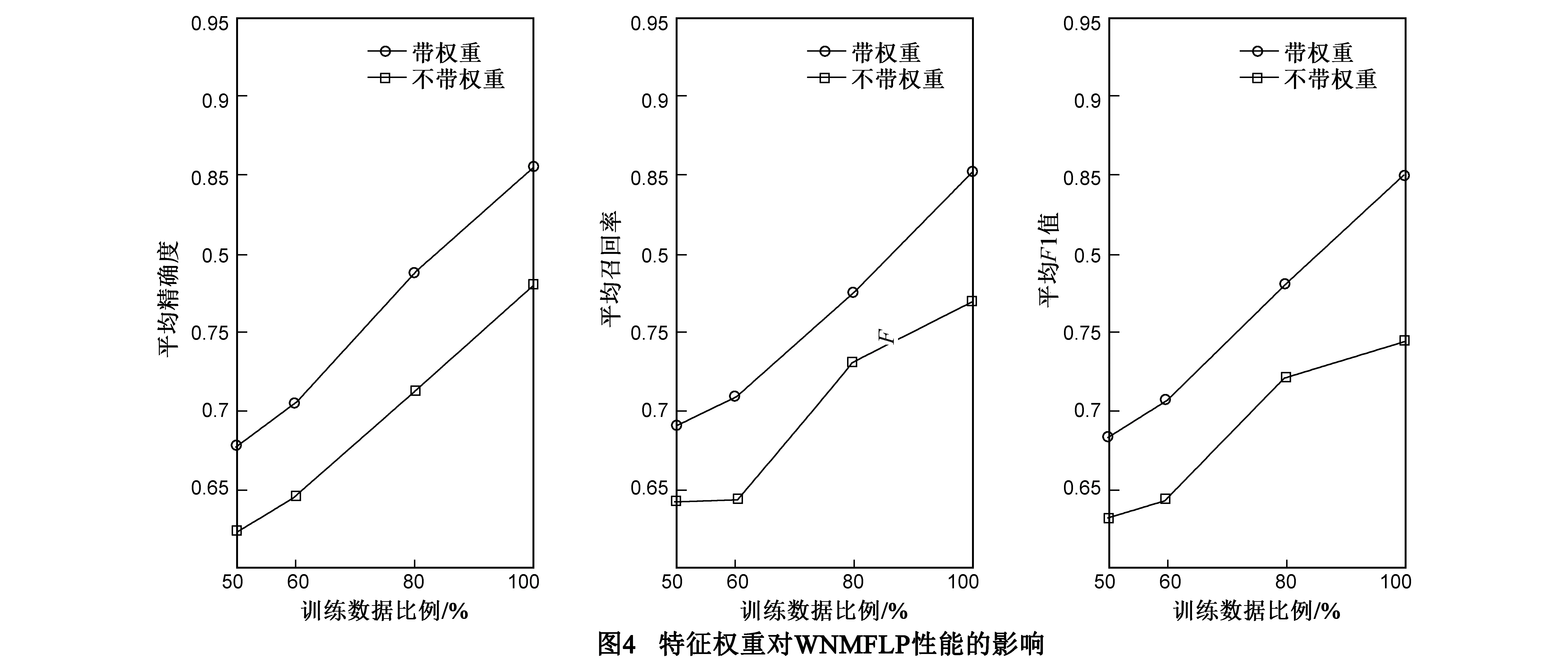
此外，本文分别在未分配权重和分配权重的数据集合上以50%，60%，80%和100%的数据作为训练集合进行10折交叉验证，实验结果如图4所示.

图4中的实验结果表明，WNMFLP在带有权重的数据集上的性能优于其在不带有权重的数据集上的性能.综上，在WNMFLP中考虑特征权重有助于提升算法性能.

5.2.3 时间信息对WNMFLP性能的影响

为验证时间信息对WNMFLP性能的影响，实验设置如下：β分别取值0.01，0.1，0.5，0.7，1，以A中50%，60%，80%和100%的数据作为训练集合进行10折交叉验证，实验结果如图5所示.

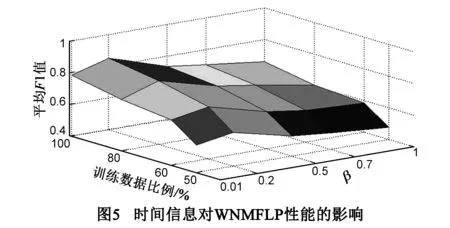
由图5可知：当β=1时，即不考虑时间信息对链接预测问题的影响，此时的F1值比峰值低很多，而当β较大时，链接预测学习过程主要受时间信息控制，此时通过学习得到的矩阵V1会出现失真，从而不能得到精确的链接预测结果.综上，将时间信息融入链接预测问题中可以有效地提高预测算法的性能.

6 结论

针对传统链接预测方法的不足，本文基于带权的动态链接预测特征集合，以用户社会关系因子约束目标函数，构建基于加权非负矩阵分解的链接预测模型，从而实现链接存在性及方向性的预测.在真实数据集上的实验结果表明，提出的算法能够有效地提高链接预测模型的性能.后续研究中，将群体智慧技术引入链接预测算法以更准确可靠地预测社会网络中的有向链接将成为主要目标.

[1]Airoldi E M,et al.Mixed membership stochastic block models for relational data with application to protein-protein interactions[A].Proceedings of ICML Workshop on Statistical Network Analysis[C].Pittsburgh,Pennsylvania,USA:Springer,2006.57-74.

[2]Hasan M Al,et al.Link prediction using supervised learning[A].Proceedings of Workshop on Link Analysis,Counter-terrorism and Security[C].Maryland,USA:SIAM,2006.322-331.

[3]Henzinger M R.Link analysis in web information retrieval[J].IEEE Data Engineering Bulletin,2000,23(3):3-8.

[4]Huang Z,et al.Link prediction approach to collaborative filtering[A].Proceedings of the 5th ACM/IEEE-CS Joint Conference on Digital libraries[C].Denver,Colorado,USA:ACM,2005.141-142.

[5]Lichtenwalter R N,et al.New perspectives and methods in link prediction[A].Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining[C].Washington,DC,USA:ACM,2010.243-252.

[6]Hasan M A,Zaki M J.A survey of link prediction in social networks[J].Social Network Data Analytics,2011,(2011):243-275.

[7]Lu L,Zhou T.Link prediction in complex networks:a survey[J].Physica A,2011,390(6):1150-1170.

[8]An J,et al.Social relation predictive model of mobile nodes in Internet of things[J].Elektronika Ir Elektrotechnika,2013,19(4):81-86.

[9]Schall D.Link prediction in directed social networks[J].Social Network Analysis and Mining,2014,4(1):1-14.

[10]Symeonidis P,Mantas N.Spectral clustering for link prediction in social networks with positive and negative links[J].Social Network Analysis and Mining,2013,3(4):1433-1447.

[11]Fire M,et al.Computationally efficient link prediction in a variety of social networks[J].ACM Transactions on Intelligent Systems and Technology,2013,5(1):10.

[12]Lou T,et al.Learning to predict reciprocity and triadic closure in social networks[J].ACM Transactions on Knowledge Discovery from Data,2013,7(2):5.

[13]Jorge V R,Alneu A L.Exploiting behaviors of communities of twitter users for link prediction[J].Social Network Analysis and Mining,2013,3(4):1063-1074.

[14]Soares Paulo R S,Prudêncio Ricardo B C.Time series based link prediction[A].Proceedings of the 2012 International Joint Conference on Neural Networks[C].Brisbane,Australia:IEEE,2012.1-7.

[15]Soares Paulo R S,Prudêncio Ricardo B C.Proximity measures for link prediction based on temporal events[J].Expert Systems with Applications,2013,40(16):6652-6660.

[16]Zhang J,et al.LaFT-tree:perceiving the expansion trace of one′s circle of friends in online social networks[A].Proceedings of the sixth ACM International Conference on Web Search and Data Mining[C].Rome,Italy:ACM,2013.597-606.

[17]Zhang J,et al.Social influence locality for modeling retweeting behaviors[A].Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence[C].Beijing,China:IJCAI/AAAI,2013.2761-2767.

[18]Leskovec J,et al.Signed networks in social media[A].Proceedings of the SIGCHI Conference on Human Factors in Computing Systems[C].Atlanta,Georgia,USA:ACM,2010.1361-1370.

[19]李乐,章毓晋.非负矩阵分解算法综述[J].电子学报,2008,36(4):737-743.

Li L，Zhang Y J.A survey on algorithms of non-negative matrix factorization[J].Acta Electronica Sinica,2008,36(4):737-743.(in Chinese)

[20]Lee D D,Seung H S.Learning the parts of objects by non-negative matrix factorization[J].Nature,1999,401(6755):788-791.

王萌萌 女，1987年出生，吉林长春人，2013年至今于吉林大学计算机学院攻读博士学位，从事社会网络分析、自然语言处理等有关研究.

E-mail:wmmwwlh@126.com

左万利 男，1957年出生,吉林长春人，博士，教授、博士生导师，从事社会网络分析、网络搜索引擎、自然语言处理等有关研究.

E-mail:wanli@jlu.edu.cn

王 英(通信作者) 女，1981年出生,吉林长春人，博士，讲师，从事社会网络分析、搜索引擎等有关研究.

E-mail:wangying2010@jlu.edu.cn

Link Prediction Model Based on Weighted Nonnegative Matrix Factorization

WANG Meng-meng1,2,ZUO Wan-li1,2,WANG Ying1,2

(1.CollegeofCompuerScienceandTechnology,JilinUniversity,Changchun,Jilin130012,China;2.KeyLaboratoryofSymbolicComputationandKnowledgeEngineering(JilinUniversity),MinistryofEducation,Changchun,Jilin130012,China)

Targeted at on-line microbloggings,on the basis of weighted and dynamic link prediction features,we utilize nonnegative matrix factorization to predict existence and directivity of link from user-based and post-based dimension by employing relationship-based factor to constrain objective function.Experiments on real-world dataset demonstrate the effectiveness of the proposed framework.Further experiments are conducted to understand the importance of features’ weights and temporal information in link prediction.

directed link prediction;nonnegative matrix factorization;features’ weights;temporal information;dynamic social networks

2015-03-30;

2015-08-03;责任编辑:马兰英

国家自然科学基金(No.61300148);吉林省科技发展计划(No.20130206051GX);吉林省科技计划(No.20130522112JH);吉林大学基本科研业务费科学前沿与交叉项目(No.201103129)

TP393.03

A

0372-2112 (2016)10-2391-07

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.10.016