基于耦合全变差的快速图像着色算法
金正猛,周 晨
(南京邮电大学理学院,江苏南京 210023)
基于耦合全变差的快速图像着色算法
金正猛,周 晨
(南京邮电大学理学院,江苏南京 210023)
本文在YCbCr色彩空间机制下,结合目标灰度图像的梯度信息,提出基于耦合全变差的图像着色模型.然后,利用交替方向乘子算法(ADMM),设计所提模型的快速数值求解算法,并给出了该算法的收敛性结果.最后,数值实验结果表明,该模型在快速着色的同时,能有效地防止颜色越界.
图像处理;图像着色;耦合全变差;交替方向乘子算法
1 引言
图像着色技术是对灰度图像人为加上彩色信息,以利于图像研究者对于图像的进一步分析和研究.图像着色技术的使用范围很广泛,可用于古画修复,给黑白影视上色、广告设计等.近年来已经出现的一些着色方法主要可分为两类,一种是基于颜色转移的着色方法,另一种是基于局部颜色扩张的着色方法.对基于颜色转移的着色方法,需要输入一幅和目标灰度图像色调相似的彩色图像作为参照图,根据一定的算法将参照图中的颜色转移到目标灰度图像中,这种方法对于参照图像的选取较为困难;对基于局部颜色扩张的着色方法则是需要人为的在目标灰度图像上画出彩色线条,再利用一些算法使彩色线条中的色彩扩展到整幅图像上,以达到着色的目的.这种方法最初由Horiuchi等人提出,他们基于“种子像素”的理念把图像中所有像素与其临近像素颜色差异的总和作为最小化目标,将图像彩色化转换为一个极值问题[1].这种方法虽在某种程度上解决图像彩色化问题,但是着色效果较差,而且计算量很大.Levin等人利用图像中所有像素与其邻域像素的色度的加权平方和最小,以实现颜色扩展的方法取得了不错的效果[2].Yatziv利用加权距离色度混合技术,找出最短路径进行快速图像彩色化[3].Heu利用像素优先确保着色后图像中的重要区域的颜色准确[4].王朔中等人在文献[5]中提出了一种各向异性的非线性扩散图像彩色化方法,通过设置自适应的张量函数,使颜色在平滑区域快速均匀扩散,在颜色交界处按各向异性方式扩散,然后采用有限差分法对扩散方程进行数值求解.近年来还出现了很多不同方法的图像着色模型,例如基于概率距离变换的图像着色[6],利用随机数据对图像重新着色已达到保边缘的作用[7],通过判别结构特征进行图像着色[8],通过结构张量改善着色效果[9]等.
本文关注的是基于局部颜色扩张变分偏微分方程着色方法.Sapiro首次将偏微分方程的方法引入到图像着色中,此模型是最小化亮度通道Y的梯度与色度通道Cb的梯度之间的差值,以此使线条颜色扩展到整幅图像[10].此模型不能很好的处理图像边界颜色定位问题,出现了边界模糊和颜色越界现象.Sung等人[11]提出了全变差着色模型,将图像着色看作图像修复问题来处理,将未涂色区域作为要修复部分,通过解优化问题得到图像的色度信息,实现颜色扩展.但是该模型着色效果不够理想,且计算速度较慢.
为了克服以上变分模型着色过程中容易出现颜色越界及计算速度较慢等缺陷.本文首先在YCbCr色彩空间中考虑图像着色问题,提出一耦合亮度通道的全变差着色模型.另外,本文利用交替方向乘子算法(Alternating Direction Method of Multipliers,ADMM),给出了耦合全变差着色模型的快速数值求解算法,并证明该算法的收敛性.最后通过数值实验验证该模型的可行性与有效性.
2 模型介绍
对目标灰度图像着色,需要在合适的色彩空间中进行.RGB彩色空间是计算机技术中使用最广泛的色彩空间之一.其它典型的色彩空间有YIQ空间(luminance,hue,and saturation)、YCbCr空间(Luminance,two color-difference components)、CB空间(Chromaticity and Brightness)等,这些色彩空间一般可将颜色图像分解为亮度(luminance)和色度(chrominance)两部分,并且与RGB空间之间都满足某种线性变换关系.以在YCbCr空间中着色为例,一般把灰度图像的灰度值作为彩色图像的亮度信息Y,如果通过某种合适的方法将该灰度图像的色度信息(Cb,Cr)恢复出来,再通过与RGB空间之间的变换关系计算出相应的R、G和B三通道的像素值,即完成了灰度图像彩色化的过程.
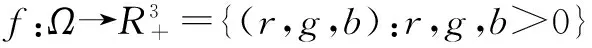
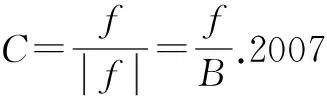
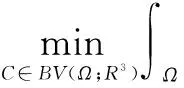
(1)
满足
|C(x)|=1,x∈Ω
(2)
其中λ为权重系数,BV(Ω;R3)为有界变差函数空间,Dc为待着色区域.由于此CB色彩空间是非凸的,导致S-R模型需满足非凸约束(2).在文献[11]中,作者用不动点算法对S-R模型进行求解.实验结果表明:S-R模型不仅着色效果不够理想,计算速度较慢,而且数值结果对参数的选取较为敏感.实际着色效果如图1中(b)所示.
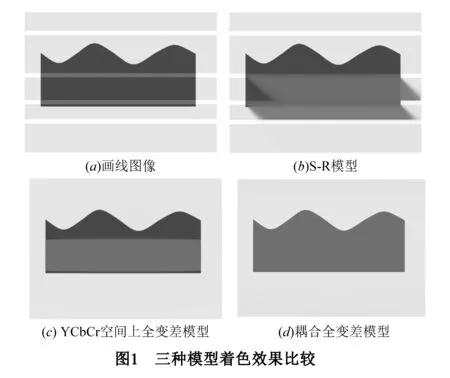
为了克服CB色彩空间非凸的缺陷,结合YCbCr凸的色彩空间,在S-R模型的基础上,我们可以得到如下的全变差着色模型:
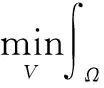
(3)
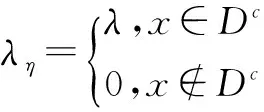
为了使扩展后的颜色与灰度图像中物体的边界充分吻合,且防止颜色越界.本文充分挖掘目标灰度图像中物体的边界信息(亮度的梯度),提出如下的耦合全变差着色模型:
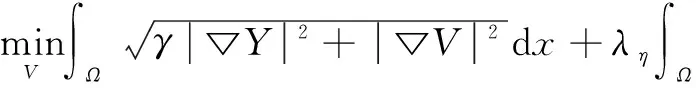
(4)
其中:γ为亮度信息的权重系数.由于该模型考虑到了目标灰度图像中物体的边缘信息,使得着色后的颜色能与目标灰度图像中物体充分匹配,且能有效防止颜色越界.实际着色效果如图1中的(d)所示.从图1可以看出,使用本文模型色彩扩展效果较好.
通过简单分析本文所提着色模型,不难发现式(4)中目标泛函关于变量V是凸的.因此我们可以利用基于凸优化的交替方向乘子(ADMM)算法,给出所提着色模型的快速数值求解算法,并证明该算法的收敛性.
3 本文算法与收敛性分析
经典的ADMM算法最早是由文献[12]提出的,本文利用ADMM算法,给出耦合全变差模型(4)的快速数值求解方法,首先令R=(γY,Cb,Cr),则式(4)转化为
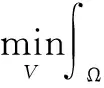
(5)
min∫Ω|d|dx+λη∫Ω|z-V0|2dx
s.td=▽R,z=V
(6)
将式(6)转化为求解无约束极值问题,得到其增广Lagrange函数如下:
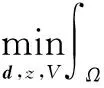
这里的λ=(λ1,λ2)是Lagrange乘子向量,γ1,γ2>0是处罚参数.
下面分别对三个子问题d,z,V进行求解:
(1)求解关于d的子问题:

等价于
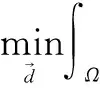
根据文献[13,14],可求出
(7)
(2)求解z的子问题:
对z进行求导并令其为0,可以解得
(8)
(3)求解V的子问题:
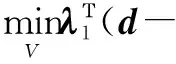
由Euler-Lagrange方程得出
再利用快速Fourier变换求出
(9)
其中F和F-1分别为快速Fourier变换及其逆变换.
结合式(7)~式(9)式,给出本文算法的具体步骤为:
Step1:令k=0,V=z=λ2=0,d=λ1=0
Step2:迭代未停止,反复执行如下步骤:
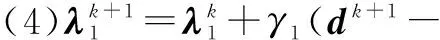
(6)k=k+1
Step3:迭代终止条件:||Vk+1-Vk|| 结合经典的ADMM算法的收敛性分析[12,15,16],下面给出本文算法的收敛性结果.由于其证明过程与文献[15,16]中完全类似,故此处省略其证明过程. 结合本文算法的具体步骤,给出本文图像着色的具体方法: 步骤1:输入一幅灰度图像,并在灰度图像上绘出适当彩色线条,此时两幅图像都是在RGB色彩空间上的. 步骤2:将两幅图像转换到YCbCr色彩空间上,分别得到两幅图像的亮度Y与色度V0=(Cb,Cr)和V=(Cb,Cr),两幅图像的亮度Y相同,V0为灰度图像的色度,V是带有彩色线条的图像. 步骤3:对λ、γ、γ1和γ2分别赋值,本文中令λ=9、γ=25、γ1=9、γ2=1,tol=10-3,利用文中所提算法求出V=(Cb,Cr),并将求出的色度赋值给原灰度图像,得到YCbCr空间上的新的图像. 步骤4:将新图像转换到RGB空间上,输出图像. 为了验证本文的算法,对大量图像进行了着色处理,并同现有算法进行比较.这里用峰值信噪比(Peak Signal to Noise Ratio,PSNR)和均方误差(Mean Square Error,MSE)来评价着色效果.其定义形式为: 其中,ftrue和f分别为原始彩色图像和着色后图像,若着色后图像的PSNR的值越大,MSE的值越小则表明图像着色后的图像与真实彩色图像越接近,着色效果越好. 实验结果如图2~图4所示,其中(a)是待处理的灰度图像,(b)是画线图像,(c)是计算S-R模型所得图像,(d)和(e)分别是用梯度下降法和本文算法得到的图像.(f)是真实的彩色图像. 表1给出了S-R模型与本文模型着色后图像的PSNR值和MSE值.表2列出了实验分别采用S-R模型,梯度下降法和本文算法对应的迭代次数和运行时间. 从图2~图4可以看出,S-R模型的着色效果较差,颜色的扩展不均匀且在边缘处有颜色越界的现象.本文耦合全变差模型在颜色扩展方面有较好效果,且能有效防止颜色越界.表1显示,对于同一张图片的着色,本文模型的PSNR值明显高于S-R模型,本文模型的MSE值小于S-R模型,由此也可看出通过本文模型着色后的图像与原彩色图像更接近,因此着色效果更好. 表1 S-R模型与本文模型着色后图像的PSNR值和MSE值 表2 S-R模型的不动点算法,本文模型的梯度下降法和本文快速算法对应的计算速度 图像算法迭代次数运行时间(s)2S-R模型的不动点算法9432.291718梯度下降法287207.484684本文算法408.1819453S-R模型的不动点算法9618.886252梯度下降法12856.967205本文算法302.8577154S-R模型的不动点算法136104.225937梯度下降法285360.859803本文算法3710.573055 从表2可以看出,在迭代终止条件相同时,S-R模型使用的算法和梯度下降法迭代步数较多且运行速度较慢,本文算法大大减少了迭代步骤,使运行更加迅速. 本文研究基于颜色扩展的变分图像着色方法,从TV着色模型(S-R模型)出发,结合目标灰度图像的梯度信息,提出了耦合全变差图像着色模型,并给出了该模型的快速数值算法.实验结果表明:该模型能有效防止着色过程中颜色在边缘处的越界,使得整体着色效果更佳.而且,所提快速算法大大提高了计算速度. [1]Takahiko Horiuchi.Colorization algorithm using probabilistic relaxation[J].Image and Vision Computing,2004,22(3):197-202. [2]Levin A,Lischinski D,Weiss Y. Colorization using optimization[A].Proceedings of ACM SIGGRAPH[C].New York,2004.684-689. [3]L Yatziv, G Sapiro. Fast image and video colorization using chrominance blending[J].IEEE Trans Image Process,2006,15(5):1120-1129. [4]Junhee Heu,Dae-Young Hyun,Chang-Su Kim,Sang-Uk Lee.Image and video colorization based on prioritized source propagation[A]. IEEE International Conference on Image Processing[C].IEEE,2009.465-468. [5]陈颖,王朔中.避免颜色越界的各向异性扩散图像彩色化[J].电子与信息学报,2014,36(2):271-277. Chen Ying,Wang Shuo-zhong.Image colorization without edge crossover of colors based on anisotropic diffusion[A].Journal of Electronics and Information Technology,2014,36(2):271-277.(in Chinese) [6]Przemyslaw Lagodzinski, Bogdan Smolka.Digital image colorization based on probabilistic distance transformation[A].International Symposium ELMAR[C]. IEEE,2008.495-498. [7]Tae Hoon Kim, Kyoung Mu Lee, Sang Uk Lee.Edge-preserving colorization usingdata-driven random walks with restart[A].IEEE International Conference on Image Processing[C].IEEE,2010.1661-1664. [8]Michal Kawulok,Jolanta Kawulok,Bogdan Smolka.Discriminative textural features for image and video colorization[J].IEICE Transactions on Information and Systems,95-D(2012):1722-1730. [9]Mark S Drew, Graham D Finlayson. Improvement of colorization realism via the structure tensor[J]. International Journal on Image Graphics,2011,11:589-609. [10]Sapiro G.Inpainting the colors[A].IEEE International Conference on Image Processing[C].IEEE,2005.698-701. [11]Sung Ha Kang, Riccardo March.Variational models for image colorization via chromaticity and brightness decomposition[J].IEEE Transactions on Image Processing,2007,16(9):2251-2261. [12]Gabay D, Mercier B. A dual algorithm for the solution of nonlinear variational problems via finite-element approximations[J].Computer and Mathematics with Applications,1976,2(1):17-40. [13]Wang Y, Yang J, Yin W, et al. A new alteranting minimization algorithm for total variation image reconstruction[J].SIAM Journal of Mathematical Imaging and Vision,2008,1(3):948-951. [14]Yang J,Yin W,Zhang Y,et al.A fast algorithm for edge-preserving variational multichannel image restoration[J].SIAM Journal of Mathematical Imaging and Vision,2009,2(2):569-592. [15]Boyd S,Parinkh N,Chu E,et al.Distributedoptimization and statistical learning via the alternating direction method of multipliers[J].Foundations and Trends in Machine Learning,2010,3(1):1-122. [16]Glowinski R, Marrocco A. Sur lapproximation parelements finis dordre un,et la resolution par penalisation-dualite dune classe de problemes de Dirichlet nonlineaires[J].Revue Francaise D’Automatique,Informatique,Recherch Operationnel,1975,9(2):41-76. 金正猛 男,1982年8月出生,博士,副教授,硕士生导师.现在南京邮电大学理学院任教,研究方向为非线性偏微分方程及其在图像处理中的应用. E-mail:jinzhm@njupt.edu.cn 周 晨 女,1990年6月出生.南京邮电大学应用数学专业硕士研究生,研究方向为基于偏微分方程的图像处理. E-mail:zhouchen1nana@126.com A Fast Coupled Total Variation Algorithm for Image Colorization JIN Zheng-meng,ZHOU Chen (SchoolofScience,NanjingUniversityofPostsandTelecommunications,Nanjing,Jiangsu210023,China) Under the YCbCr color space mechanism,we propose a coupled total variation model for image colorization by combining the gradient of target grayscale image.Then we design a fast algorithm to solve the proposed model numerically by incorporating the alternating direction method of multipliers(ADMM) algorithm,and give the convergence results of the proposed algorithm.Finally,experimental results are reported,demonstrating that the proposed model can effectively prevent colors from crossing over the edges of the target grayscale image during fast colorization. image processing; image colorization; coupled total variation; alternating direction method of multipliers(ADMM) algorithm 2015-03-13; 2016-04-12;责任编辑:李勇锋 国家自然科学基金重大研究计划(培育项目)(No.91330101);江苏省高校自然科学基金(No.15KJB110018);江苏省省级重点STITP(No.SZDG2015028);南京邮电大学科研基金(No.NY215088) TN911.73 A 0372-2112 (2016)10-2364-06 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.10.012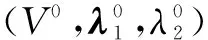
4 着色具体操作步骤与实验结果分析


5 结束语



