一种适用于分布式摄像机网络的SCIWCF算法

陈彦明,赵清杰,刘若宇

(北京理工大学计算机学院智能信息技术北京市重点实验室,北京 100081)



一种适用于分布式摄像机网络的SCIWCF算法

陈彦明,赵清杰,刘若宇

(北京理工大学计算机学院智能信息技术北京市重点实验室,北京 100081)

本文使用容积卡尔曼滤波器来处理分布式摄像机网络中的目标跟踪问题.平方根容积信息滤波(Square-Root Cubature Information Filter,SCIF)是容积卡尔曼滤波的一种扩展,其具有有效性和可靠性等方面优势,有利于对多源信息进行信息融合.然而当该算法应用于像摄像机网络这种大规模网络时,如果采用一般的集中式处理,中心节点可能会承受较大的计算压力.针对这个问题,本文首先将平方根容积信息滤波器进行了扩展,提出分布式平方根容积信息滤波器,使其能适应大规模网络.另外在摄像机网络中,由于摄像机装置在一个较大的区域内,由于摄像机观测区域有限,目标可能会出现在观察的盲区,这样就会存在某些摄像机的测量数据无效.针对这个问题,本文提出了平方根容积信息加权一致性滤波器(Square-Root Cubature Information Weighted Consensus Filter,SCIWCF)对状态信息和信息矩阵加权,减小这些无效信息在一致性算法的作用,从而提高整体的滤波性能.仿真实验结果表明,本文提出的算法能够在摄像机网络中对目标进行有效跟踪,在估计精度和滤波器稳定性等方面要优于传统的信息滤波.

容积卡尔曼滤波;信息滤波;一致性算法;分布式摄像机网络

1 引言

摄像机网络(Camera Networks)作为无线传感器网络(Wireless sensor networks,WSN)的一个分支,近来受到了越来越多人的关注和研究[1～6].然而限于成本和能耗的考虑,通常意义上的传感器网络节点都是由一些低功耗和低成本的硬件组成,这就使得很多算法在传感器网络中无法施展应用.另外由于传感器网络的大规模性,导致一般的集中式处理算法并不实用.集中式处理不仅会过快地消耗掉中心点附近的节点的能量,而且对中心节点的网络带宽和处理能力带来更大的考验.因此分布式算法在传感器网络中的优势越来越明显.

分布式估计作为一种分布式算法,由于具有可扩展性和容错性,已经被用于摄像机网络中的目标跟踪问题[4].在基于分布式估计的目标跟踪中,每个摄像机节点利用自身的信息与接收到的周围的邻居节点的信息进行信息融合,然后预测和估计目标的状态信息(位置、速度等).

在分布式估计中,系统必须采用一定的策略来协同各个局部节点的信息,使得局部节点获得全局信息.近来很多学者提出用一致性算法来优化每个节点的信息,使每个节点的信息达到一致[7,8].结合一致性算法,再运用类卡尔曼滤波算法就能实现分布式的目标跟踪.如,Olfati-Saber 等人提出一种分布式卡尔曼滤波器(Distributed Kalman Filtering, DKF)应用于传感器网络中[9],但该滤波器并没有考虑朴素节点(naive node)[4]的存在会导致一致性算法的发散.尽管在2008年作者又提出了一种异构的两层网络结构来解决这个问题[10].但该结构并不是完全的分布式网络,并不能有效的应用于大规模网络中.针对这个问题,Kamal等人提出一种加权形式的信息一致滤波(Information weighted consensus filters,IWCF)[4],该滤波器利用对状态信息和信息矩阵进行加权从而避免朴素节点的影响.Katragadda S等人针对文献[4]只是用于线性系统的事实,利用类似于扩展卡尔曼滤波器的推导的方法对非线性方程进行一阶泰勒展开使其能适用于非线性系统中[11].但由于只采用了一阶泰勒展开,往往算法的精度达不到系统要求,并且由于处理器字长问题可能会导致算法失效[12].这种情况对于采用处理能力较弱的微处理器的传感器网络来说更为严重.

针对这些问题,并根据摄像机网络这一特定应用,本文提出一种平方根容积卡尔曼滤波器一致性滤波算法.本文所基于的平方根容积卡尔曼滤波器是由Arasaratnam等人提出的[12],其类似于无迹卡尔曼滤波器[13],但比无迹卡尔曼滤波器更具有鲁棒性和应对高维非线性问题能力[12].

由于信息滤波器特殊的信息形式,有利于简化多源信息融合.在信息滤波器中,多源信息的融合可以表达成简单的累加操作[14].因此本文采用容积卡尔曼滤波器的信息滤波形式:平方根容积信息滤波器.

2 前提知识

在介绍容积信息滤波之前,本节先介绍一下本文后续需要用到的一些前提知识.

2.1 模型描述

如前文所述,之前很多的研究都假设摄像机网络的目标跟踪问题满足线性系统方程,但实际中,真正的线性系统并不存在,真实的系统总存在一些非线性,目标跟踪问题也不例外.本文采用的节点i离散时间系统的系统方程表示如下(所有节点的系统方程形式一致):

(1)

(2)

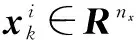
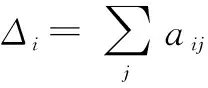
2.2 分布式平均一致性算法

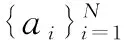
在平均一致性算法中,每个节点初始化其一致性状态为ai(0)=ai并且运行下面的迭代式,

(3)

在开始进行第τ轮迭代时,节点Ci将它的前一个状态值ai(τ-1)发送给它的直接邻居Cj∈Ωi,并且同时接收邻居节点前一个状态值aj(τ-1),然后用式(3)更新当前值.经过几轮迭代后,网络中各个节点的状态值收敛于初始状态的平均值.参数ε决定了算法的收敛速度,其取值范围为0～1/Δmax,其中Δmax是网络图G的最大度.选择大的ε会加快算法的收敛速度,但如果ε的取值大于1/Δmax会导致系统发散.

3 分布式平方根容积信息滤波

平方根容积滤波器是由Arasaratnam提出的一种新型滤波器[12,18],其诸多优点近来得到广泛的应用.但文献[18]采用的是集中的方式来进行数据的融合,系统中存在一个数据融合中心,并且该文献假定各个节点收集的数据相互独立.由于摄像机网络中各个摄像机对目标的跟踪具有很大的耦合性,导致文献[18]观测数据相互独立的假设并不成立.另外如前文所述,分布式的数据处理更合适摄像机网络中信息融合.基于这些原因,本文提出一种分布式的容积信息滤波算法.

在考虑分布式平方根容积信息滤波器之前,首先回顾一下集中情况下的表达.

3.1 集中式SCIF(Centralized SCIF, CSCIF)

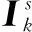
(4)

(5)

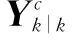
(6)

(7)

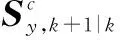
在大规模摄像机网络中,一般情况网络不存在中心节点,网络中的所有节点地位对等.那么如果在这种网络中进行信息融合,就需要一种分布式的处理方法.本文第二节介绍的平均一致性算法满足这种网络的需求.本节将基于一致性策略提出一种分布式平方根容积信息加权一致性滤波(Square-Root Cubature Information Weighted Consensus Filter, SCIWCF).

在平均一致性算法中,节点s仅仅需要与其周围的邻居节点进行通信,就可以达到整个网络状态的一致.假如网络已经收敛到一个平均值时,此时所有节点的信息将和平均值一样,这样导致每个节点的信息都具有冗余.另外摄像机网络中存在朴素节点的情况.上文所述的朴素节点是指在一个观测区域内,假如目标只可以被节点s观测到,节点s以及其直接邻居节点j∈Ωs可以通过直接的信息交换而得到观测目标,然而其他的节点m,m∉{s∪Ωs}并不能直接得到观测目标,而需要经过多跳网络传输才能得到目标.在存在朴素节点时,如果对所有的信息都同等对待,会导致最终的状态收敛到一个不正确的值.

在文献[4]中,Kamal等人提出了一个用1/Nc加权信息矩阵和信息向量的分布式状态估计算法.该算法可以有效减少节点间信息的冗余,并且可有效抑制朴素节点的影响.本文使用类似策略来处理平方根容积信息矩阵和信息向量.

其计算过程如下:

(8)

(9)

(10)

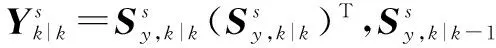
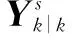
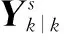
(11)

为了便于处理,上式用P=AAT来替代,尽管A可以看成P的平方根,但为了便于计算,本文采用QR分解先将A转化为一个三角阵S,记为:

S=Tria(A)

(12)

在QR分解计算中,可以将AT分解为一个正交矩阵Q和一个上三角矩阵R,AT=QR,此时P=AAT可以写成:

P=AAT=RTQTQR=RTR=SST

(13)

故S=RT,且式(13)只需要求出R即可.S是一个下三角矩阵,其具有稀疏性将有利于计算和减小存储空间.

从上面的分析可知,式(8)和式(11)等价.

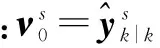
Fork=1 toK

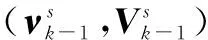
更新一致项:

(14)

(15)

END For

下面给出式(14)的推导过程.

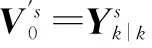
(16)

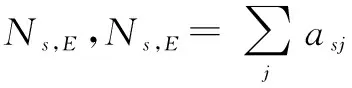
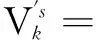
(17)

然后对式(17)进行QR分解,可以得到式(14)的形式,具体过程可以仿照步骤1进行,这里不再赘述.

(3)计算后验信息向量和信息矩阵:

(18)

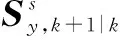
上面计算过程的前3步为量测更新过程,最后1步为时间更新过程.在实际使用中,根据给出先验信息的不同,两者执行次序可以互换.

分布式SCIWCF算法总结于算法1.

算法1 摄像机Cs的分布式SCIWCF算法

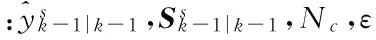
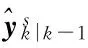
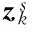
(5)根据3.2节的步骤2)进行平均一致性算法的K轮迭代

(6)根据式(18)计算k时刻的后验信息

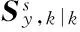
3.3 算法收敛性

针对3.2节提出的算法,本节进一步对它的收敛性做简单阐述.

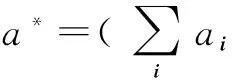
关于引理1的证明具体可以参考文献[7]中的定理2的证明.式(16)和(15)与式(3)有类似的形式,且式(16)和(14)等价,另外引理1的所需条件3.2节的分布式SCIWCF算法均能满足,因此容易证明本文提出的SCIWCF算法可以收敛于初值的平均一致值.

3.4 算法性能分析

下面分析一下本文提出的分布式SCIWCF算法性能.

3.4.1 算法等价性

在SCIF算法中,Ik和ik可以表示如下[18]:

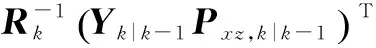
(19)

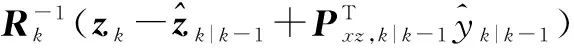
(20)

[21]中的方法,定义一种伪观测矩阵:

(21)

则Ik和ik可以重新表示如下:

(22)

(23)

根据式(22)、(23),考虑节点编号,并用上标“+”表示后验估计,上标“-”表示先验估计,下标“c”代表集中式处理,则可以将集中式SCIF中式(4)(5)改写为:

(24)

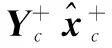
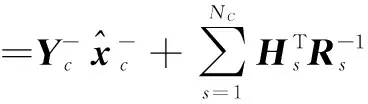
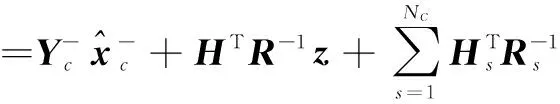
(25)

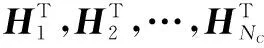
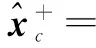
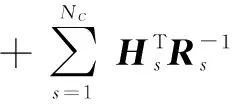
(26)

其中uc=HTR-1z.

从上面的推导可知,式(24)和式(26)与集中式SCIF算法中的式(4)和式(5)等价.

定理1 假设摄像机网络包含n个节点,通信拓扑由无向连通图G表示,0<ε<1/Δmax,Δmax是网络图G的最大的度,对这n节点执行分布式SCIWCF算法,则当算法达到平均一致值时,各节点量测更新过程中的状态估计和误差协方差矩阵与集中式算法求得值等价.

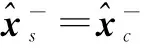
(27)

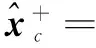
(28)

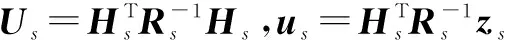
从上面的推导可以看出,当所有节点收敛到平均一致值时,式(27)和式(28)分别与式(24)和式(26)等价.

(29)

(30)

根据Us和us的定义,以及式(22)(23)中Ik和ik,可将式(29)和(30)等价于下面两式:

(31)

(32)

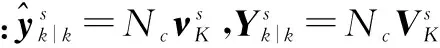
因此在k以后的时刻,分布式SCIWCF算法结果与集中式SCIF一致.

□

从定理1可以知道,本文提出的SCIWCF算法在在K→∞时,算法能达到与集中式算法一致的结果.尽管在实际实现中,平均一致性算法中不可能达到完全的一致,即K不可能趋近于无穷大.但是,从后面的仿真实验可以看出,SCIWCF算法能够很快收敛于近似的平均一致值,因此本文提出的算法具有实际意义.

3.4.2 通信代价

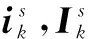
(33)

其中L为迭代次数.

而对本文提出的SCIWCF算法和EIWCF[11]算法一样,每个节点每次迭代发送的均是局部状态估计和信息矩阵.同协方差矩阵一样,信息矩阵也是正定矩阵,因此也只需要对应的传输上三角或者下三角阵.这两个算法通信代价T记为:

(34)

结果见图1.

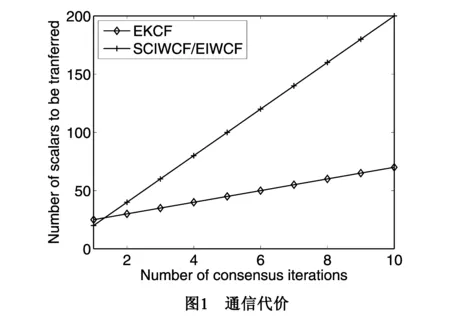
从图中可以看出,随着迭代次数的增加,SCIWCF(或EIWCF)算法的通信代价也线性增加,并且其通信代价要高于EKCF算法.但从后面的仿真实验可以看出,尽管略微增加了通信代价,但是SCIWCF算法却大大提高了估计精度.

4 实验仿真

本节将本文提出的算法与其他在摄像机网络中常用非线性算法进行对比:EIWCF[11]和EKCF[23].本文的所有实验是在一台装有Matlab软件的CPU为Intel 3.4Ghz,内存为4GB的Windows 7 32bit主机上完成的.

4.1 仿真场景

在一个目标在500m×500m的区域运动,区域内分布式的布置了9个摄像机.一般来说摄像机的感知区域是一个扇形区域,但为了便于仿真,本文假定每个摄像机的感知区域为其周围的200m×200m区域[11].目标的状态向量由x,y方向的位移和速度,以及一个时间同步因子组成.记为:xk=[xkykvxvyδk]T.目标的运动模型如下[22]:

(35)

其中(xk,yk)为目标在参考平面上的位置,(vx,vy)为目标速度,δk为连续的两次测量之间的时间间隔.由于目前的时间同步算法都存在误差,本文的仿真中不假定精确的时间同步,同步误差用一个时间不确定因子e表示,假设e也满足高斯分布.本文仿真中假定v=(ax,ay,e)满足高斯白噪声[22],其方差Q=diag([1 1 0.001]).本文中目标的初始运动速度在10m/s到50m/s之间随机选取,并且目标的初始运动方向从0到2π之间随机产生.

摄像机的测量模型如下:

(36)

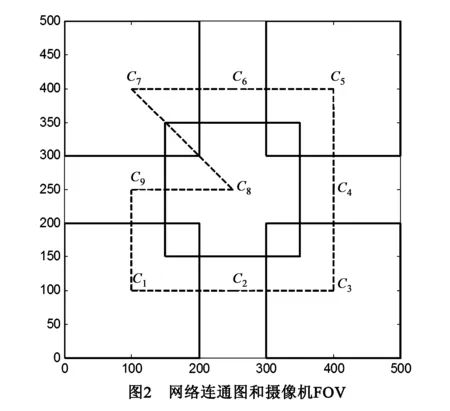
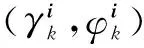
本文采用度为2稀疏连通网络来验证来算法的性能.如图2所示虚线连接.图中其他实线代表的是摄像机的FOVs(由于FOVs存在重叠,为了便于显示,图中只标示出了C1,C3,C5,C7,C8的FOV,其他摄像机类似),例如C1的观测区域为以C1为中心的200m×200m区域.

4.2 仿真结果

下面介绍一下本文提出的三种算法的仿真结果.在仿真中,同文献[11]一样,本文采用蒙特卡罗的方法分别也对三种算法进行20次仿真,仿真结果用均值误差和其对应的估计误差的方差表示.

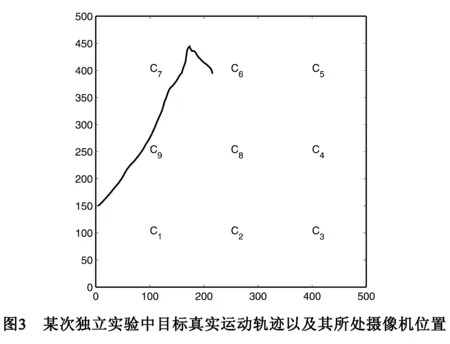
在某次独立实验中,目标的真实运动轨迹如图3所示.图3中,由于摄像机的可视区域受限,不同时刻只有C1,C9,C7,C6能直接观测到目标.因此该次实验中,存在上文提到的朴素节点的情况.

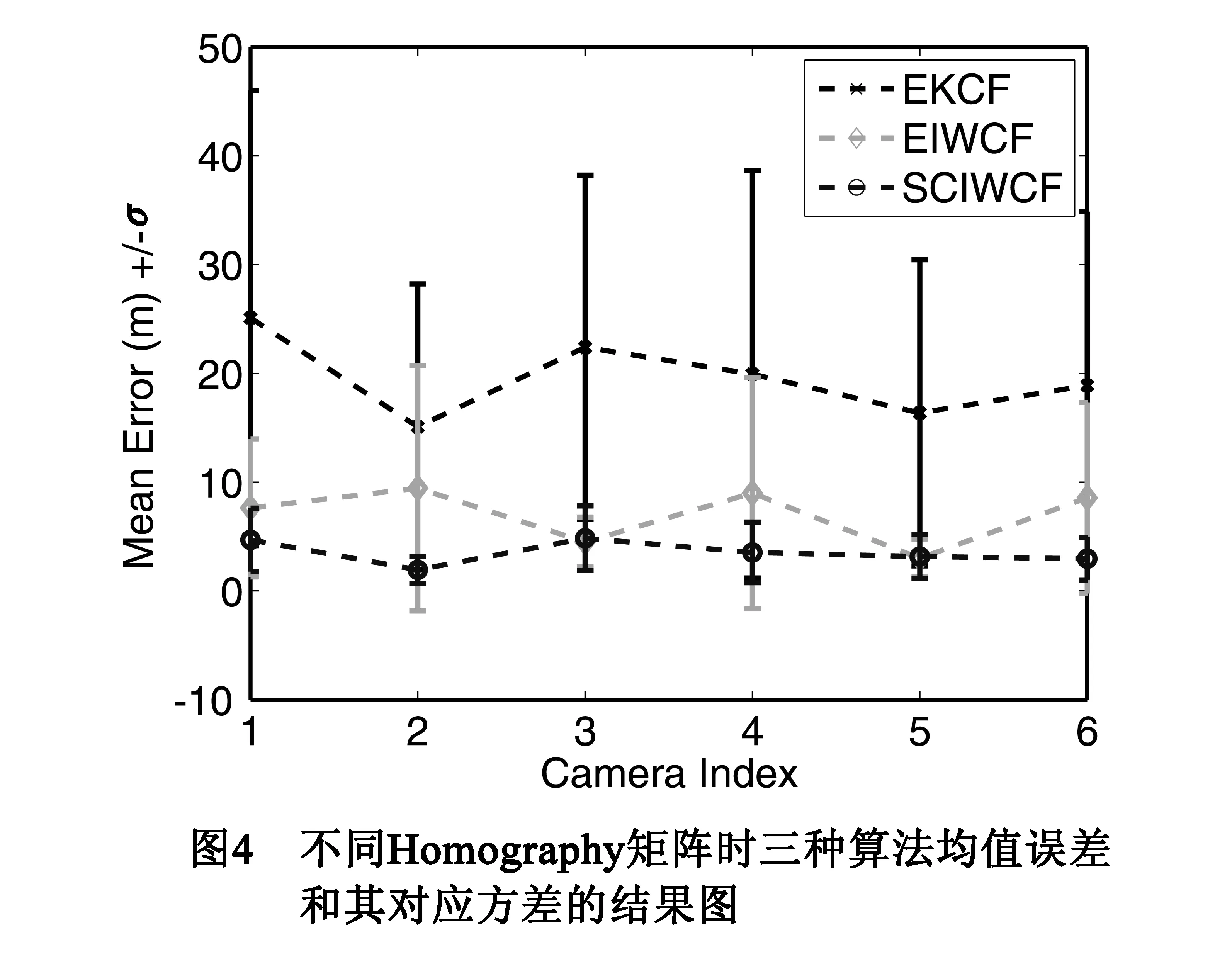
本文采用的Homography矩阵来源于APIDIS数据集[24]中的篮球比赛序列的摄像机参数.APIDIS数据集使用6个摄像机来观测比赛情况,不同的摄像机有着不同的Homography矩阵,因此有着不同的观测方程.图4显示的是在固定平均一致性算法迭代次数为8次时,取不同Homography矩阵三种算法均值误差和其对应的方差的结果图.从图中我们可以看出,EIWCF和本文的算法都能很好的适应不同Homography矩阵的变化,但本文的算法变化幅度更小.因此本文算法针对不同观测方程鲁棒性更好.

由于Homography矩阵取值不影响不同算法的对比,因此在后面的实验中本文取APIDIS数据集中摄像机C6对应的Homography矩阵为9个摄像机的参数,对应的取值为:

(37)

所有摄像机取相同的Homography矩阵并不会影响仿真效果.因为Homography矩阵只是将摄像机的观测平面转化到参考平面上.实际使用中可以将每个摄像机的Homography矩阵设置为不同,但为了使仿真环境简单易实现,本文才取了相同的Homography矩阵.

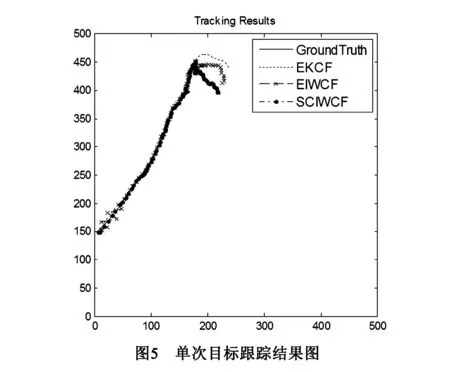
图5显示的是EKCF,EIWCF和SCIWCF算法单次目标跟踪的结果图.从图中可以看出,在本次实验中,三种算法都能很好的跟踪到目标.这是因为这些算法都采用了平均一致性算法(图中显示的是8轮迭代的结果).不过通过对比,SCIWCF算法更加贴合真实运动轨迹,也就是说SCIWCF算法更加适合于多摄像机协同跟踪这一应用.

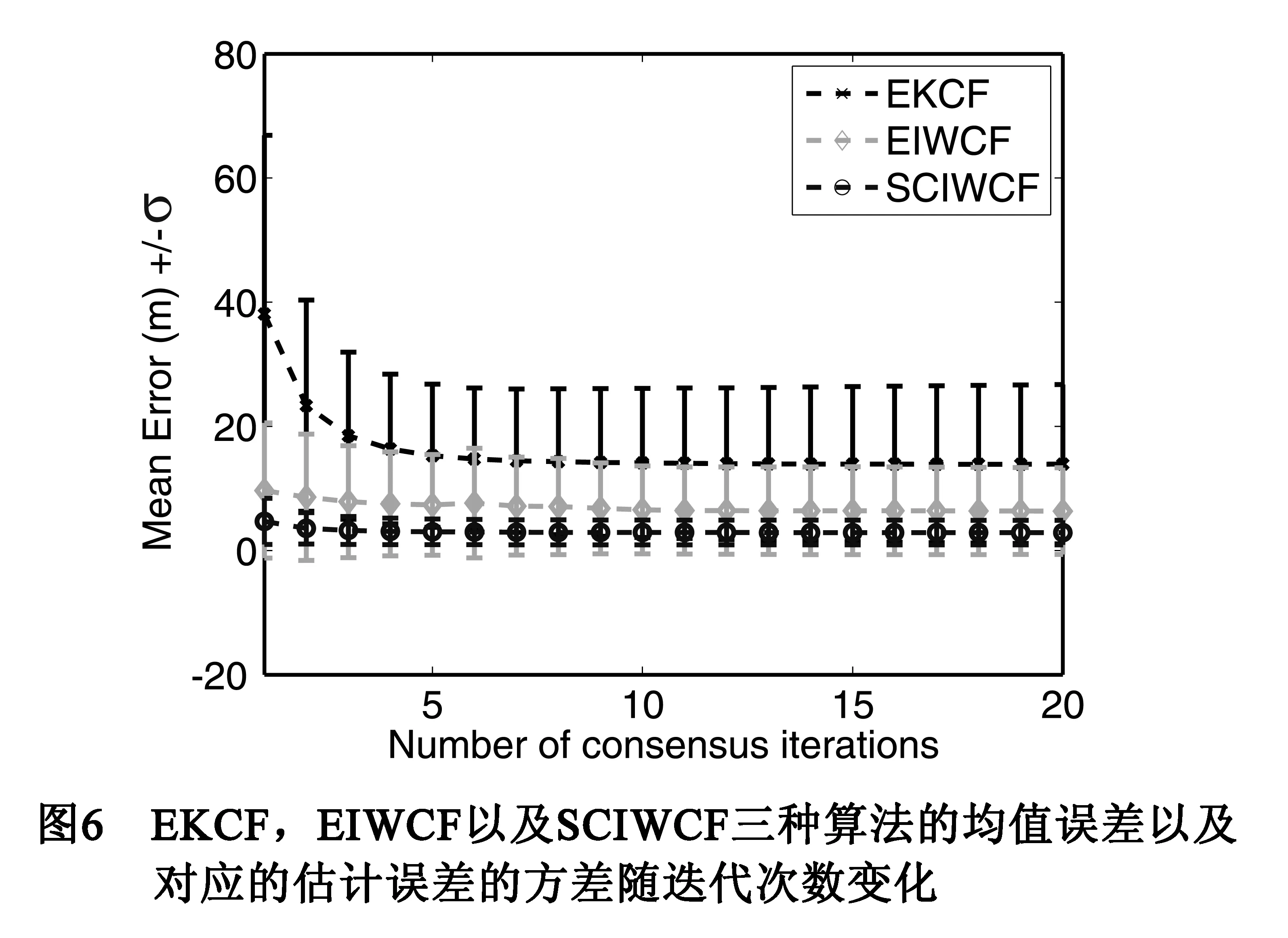
图5显示的只是单次结果,结果有随机性,并不能很好的体现出各种算法的性能差别.下面对EKCF,EIWCF和SCIWCF三种算法分别做20次蒙特卡罗仿真,图6显示了三种算法均值误差和其对应的方差.从图6中可以看出,本文提出的算法能有效的跟踪目标,并且进行了6轮迭代,算法就收敛到一致平均值.因此在实际使用该算法时,可以在相邻时间间隔内,进行多次迭代.由于迭代只在相邻节点间进行,因此速度可以很快.这样算法的实时性就可以得到保证.另外在上面的实验中,Q的取值为Q=diag([1 1 0.001]),随着在实验中加大Q的取值,EKCF和EIWCF算法常常会出现跟踪不上目标的情况,而本文提出的算法却具有很好的鲁棒性.因此本文提出的算法能有效及快速解决摄像机网络协同跟踪问题.

本文的实验是基于Matlab实现的.在Matlab中,默认情况下,所有数值计算的精度都是double型的.根据IEEE 754标准double精度的数值采用64位来表示.为了验证三种算法在有限字长计算机中的性能,本文用single函数将算法程序中所有double精度的数值转化为单精度(32位).不幸的是如果采用单精度数值,EKCF和EIWCF算法往往得不到正确的数值.这是因为在进行矩阵逆运算时如果采用单精度数值,往往会导致结果矩阵不正定.在仿真中,经常会出现“Matrix is close to singular or badly scaled.Results may be inaccurate.”这样的警告信息.而本文提出的SCIWCF算法却没有出现这个问题.

5 结论

本文结合容积卡尔曼滤波,提出了一种适用于摄像机网络的平方根容积信息加权一致性滤波算法.该算法具有较强的健壮性,能有效克服大规模摄像机网络的节点分布稀疏性而导致的滤波发散.另外本文所提出的SCIWCF算法可以有效解决摄像机网络中的达到一致性后的节点状态信息冗余问题.本文提出的算法在仿真实验中表现出了极好的性能,如由图6的数据可知,本文提出SCIWCF算法的均方根误差(Root mean square error,RMSE)比EIWCF提高50%左右.但本文仅针对随机产生的轨迹进行了仿真,并没有用到真实的环境仿真.由于本文提出的SCIWCF算法可以有效解决嵌入式处理器有限字长问题而导致算法在更新信息矩阵使该矩阵非正定,进而使算法失效.因此本文提出的算法可以很好的应用于嵌入式环境中,有利于在大规模摄像机网站中的应用.本文的下一步工作是将SCIWCF算法运用到现实应用中,进而来验证本文提出算法实用性.

参考文献

[1]Akyildiz I F,Melodia T,Chowdhury K R.A survey on wireless multimedia sensor networks[J].Computer Networks,2007,51(4):921-960.

[2]Soto C,Song B,Roy-Chowdhury A K.Distributed multi-target tracking in a self-configuring camera network[A].Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition(CVPR)[C].Florida,USA:IEEE,2009.1486-1493.

[3]Wan J,Liu L.Distributed data association in smart camera networks using belief propagation[J].ACM Transactions on Sensor Networks (TOSN),2014,10(2):1-24.

[4]Kamal A T,Farrell J A,Roy-Chowdhury A K.Information weighted consensus filters and their application in distributed camera networks[J].IEEE Transactions on Automatic Control,2013,58(12):3112-3125.

[5]蒋建国,顾占冰,胡珍珍,齐美彬.多摄像机视域内的目标活动分析[J].电子学报,2014,42(2):306-311.

Jiang Jian-guo,Gu Zhan-bing,Hu Zhen-zhen,Qi Mei-bin.Activity analysis cross muti-camera[J].Acta Electronica Sinica,2014,42(2):306-311.(in Chinese)

[6]Chen Y M,Zhao Q J.A novel square-root cubature information weighted consensus filter algorithm for multi-target tracking in distributed camera networks[J].Sensors,2015,15(5):10526-10546.

[7]Olfati-Saber R,Fax J A,Murray R M.Consensus and cooperation in networked multi-agent systems[J].Proceedings of the IEEE,2007,95(1):215-233.

[8]Ren W,Beard R W.Consensus seeking in multiagent systems under dynamically changing interaction topologies[J].IEEE Transactions on Automatic Control,2005,50(5):655-661.

[9]Olfati-Saber R.Distributed Kalman filtering for sensor networks[A].In:Proceedings of 46th IEEE Conference on Decision and Control[C].New Orleans,Louisiana,USA:IEEE,2007.5492-5498.

[10]Olfati-Saber R,Sandell N F.Distributed tracking in sensor networks with limited sensing range[A].American Control Conference[C].Seattle,Washington,USA:IEEE,2008.3157-3162.

[11]Katragadda S,SanMiguel J C,Cavallaro A.Consensus protocols for distributed tracking in wireless camera networks[A].The 17th International Conference on Information Fusion[C].Salamanca,Spain:IEEE,2014.1-8.

[12]Arasaratnam I,Haykin S.Cubature kalman filters[J].IEEE Transactions on Automatic Control,2009,54(6):1254-1269.

[13]Julier S J,Uhlmann J K.Unscented filtering and nonlinear estimation[J].Proceedings of the IEEE,2004,92(3):401-422.

[14]Mutambara A G O.Decentralized Estimation and Control for Multisensor Systems[M].Florida:CRC press,1998.68-75.

[15]Godsil C D,Royle G,Godsil C D.Algebraic Graph Theory[M].New York:Springer,2001.279-282.

[16]Olfati-Saber R,Murray R M.Consensus problems in networks of agents with switching topology and time-delays[J].IEEE Transactions on Automatic Control,2004,49(9):1520-1533.

[17]Boyd S,Diaconis P,Xiao L.Fastest mixing Markov chain on a graph[J].SIAM review,2004,46(4):667-689.

[18]Arasaratnam I.Sensor fusion with square-root cubature information filtering[J].Intelligent Control and Automation,2013,4:11-17.

[19]Arasaratnam I,Haykin S,Hurd T R.Cubature Kalman filtering for continuous-discrete systems:theory and simulations[J].IEEE Transactions on Signal Processing,2010,58(10):4977-4993.

[20]Casbeer D W,Beard R.Distributed information filtering using consensus filters[A].2009 American Control Conference[C].Missouri,USA:IEEE,2009.1882-1887.

[21]Lee D J.Nonlinear estimation and multiple sensor fusion using unscented information filtering[J].IEEE Signal Processing Letters,2008,15:861-864.

[22]Medeiros H,Park J,Kak A C.Distributed object tracking using a cluster-based kalman filter in wireless camera networks[J].IEEE Journal of Selected Topics in Signal Processing,2008,2(4):448-463.

[23]Ding C,Song B,Morye A,et al.Collaborative sensing in a distributed PTZ camera network[J].IEEE Transactions on Image Processing,2012,21(7):3282-3295.

[24]Chen F,Delannay D,De Vleeschouwer C.An autonomous framework to produce and distribute personalized team-sport video summaries:A basketball case study[J].IEEE Transactions on Multimedia,2011,13(6):1381-1394.

陈彦明 男,1983年出生,安徽安庆人,北京理工大学博士研究生,主要研究方向为图像处理,无线传感器网络,智能计算.

E-mail:cym@bit.edu.cn

赵清杰(通信作者) 女,1966年出生,河南南阳人,北京理工大学计算机学院教授,博士生导师.2003年获得清华大学计算机科学与技术学院博士学位.主要研究方向包括图像与视频处理,机器视觉,智能计算.

E-mail:zhaoqj@bit.edu.cn

刘若宇 男,1990年出生,河北唐山人,北京理工大学计算机学院硕士研究生.主要研究方向为系统建模.

E-mail:2120131043@bit.edu.cn

A Novel Square-Root Cubature Information Weighted Consensus Filter Algorithm for Distributed Camera Networks

CHEN Yan-ming,ZHAO Qing-jie,LIU Ruo-yu

(BeijingKeyLaboratoryofIntelligentInformationTechnologySchoolofComputerScience,BeijingInstituteofTechnology,Beijing100081,China)

This paper deals with the problem of tracking target in a distributed camera network using the cubature Kalman filter.The square-root cubature Information filter (SCIF) is an extension of the cubature Kalman filter.It is an efficient and robust non-linear filter for multi-sensor data fusion.However,when this algorithm is applied to large-scale networks such as camera networks,the center node may be imposed on severe computational loads if using centralized multi-sensor system.In order to solve this problem,a distributed algorithm based on square-root cubature information filter is presented for large-scale networks.In camera networks,because cameras are arranged in a larger region,the target may appear in the blind zone due to the limited field of view (FOV).This may produce invalid measurements from some cameras.To overcome this problem,this paper proposes a novel square-root cubature information weighted consensus filter (SCIWCF) which reduces the effect of these invalid measurements in consensus algorithm via proper weighting on the information vector and information matrix.The simulation results show that the proposed algorithm can efficiently track the target in camera networks,and is obviously better in terms of its accuracy and stability than the traditional Information filter.

cubature Kalman filter;information filter;consensus algorithm;distributed camera networks

2015-04-21;

2015-07-06;责任编辑：蓝红杰

国家自然科学基金(No.61175096);北京市教育委员会共建项目专项

TP393

A

0372-2112 (2016)10-2335-09

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.10.008