基于稀疏补分析模型的近似最优子空间追踪
张宗念,李金徽,黄仁泰,闫敬文
(1.东莞理工学院电子工程学院,广东东莞 523808;2.东莞理工学院网络中心,广东东莞 523808;3.东莞理工学院计算机学院,广东东莞 523808;4.汕头大学电子工程系,广东汕头 515063)
基于稀疏补分析模型的近似最优子空间追踪
张宗念1,李金徽2,黄仁泰3,闫敬文4
(1.东莞理工学院电子工程学院,广东东莞 523808;2.东莞理工学院网络中心,广东东莞 523808;3.东莞理工学院计算机学院,广东东莞 523808;4.汕头大学电子工程系,广东汕头 515063)
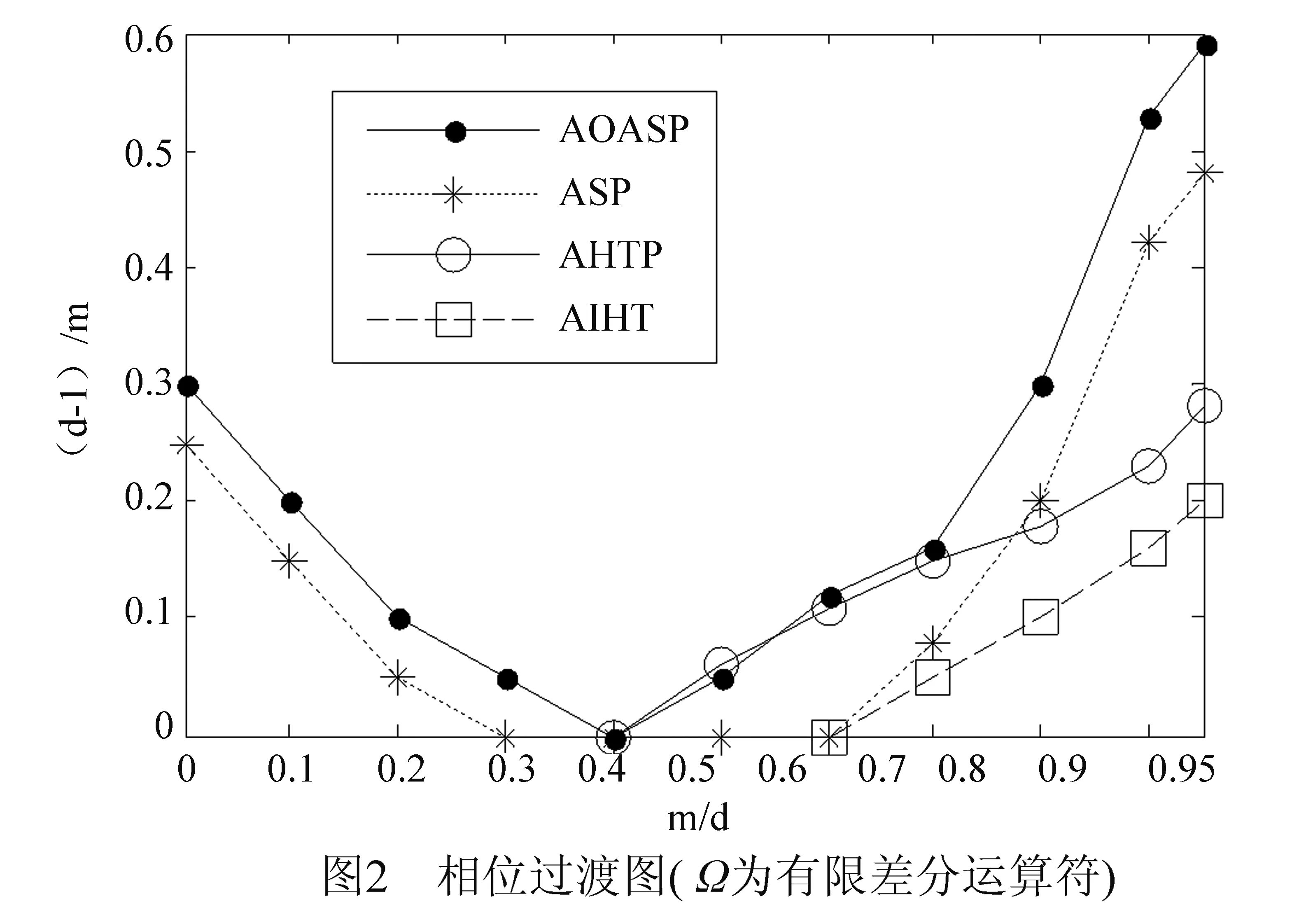
为了从含噪声的测量矢量中重构原始信号,研究了稀疏补分析模型下近似最优子空间追踪信号重构算法.针对直接采用稀疏综合模型下子空间追踪过程非最速梯度下降和信号重构概率不高的缺点,根据稀疏补分析模型下不同类型分析字典的结构特点来设计近似目标优化函数;改进了迭代追踪过程;优化了稀疏补取值方法;提出并实现了基于稀疏补分析模型的近似最优分析子空间追踪算法.仿真实验证明,当稀疏补运算符分别采用随机紧支框架和二维全变分矩阵时,算法的完全重构信号概率均明显高于ASP、AHTP、AIHT、AL1、GAP算法的完全重构信号概率;对于含高斯噪声的输入信号,算法的重构信号综合平均PSNR比相应的ASP、AHTP、AIHT算法分别提高了0.8dB、1.38dB、3.13 dB,但比GAP和AL1算法降低了0.32 dB和0.6dB.算法的完全重构概率与综合重构性能有了明显提高,收敛充分条件得到进一步简化.
稀疏补分析模型;近似最优;子空间;追踪
1 引言
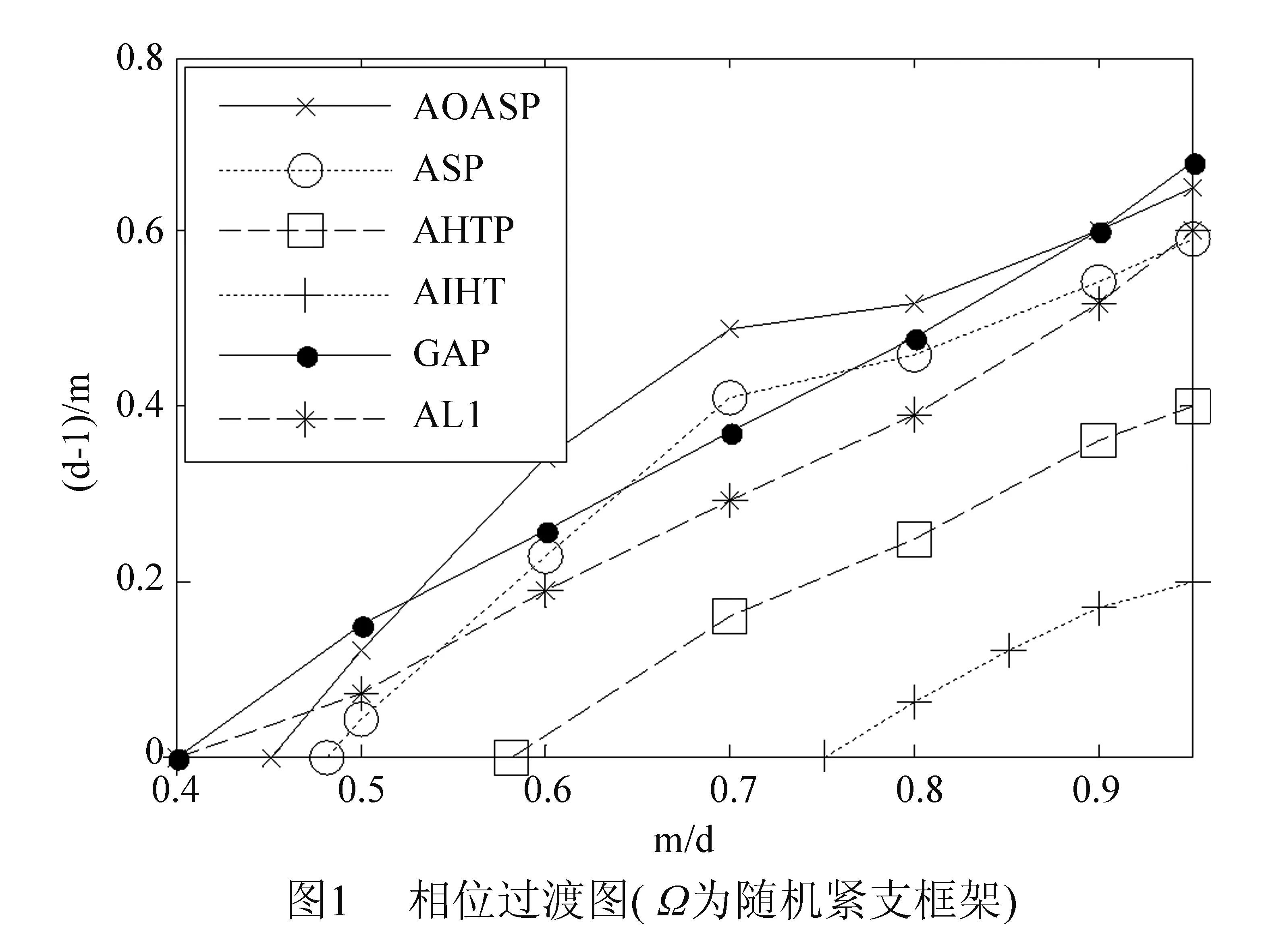
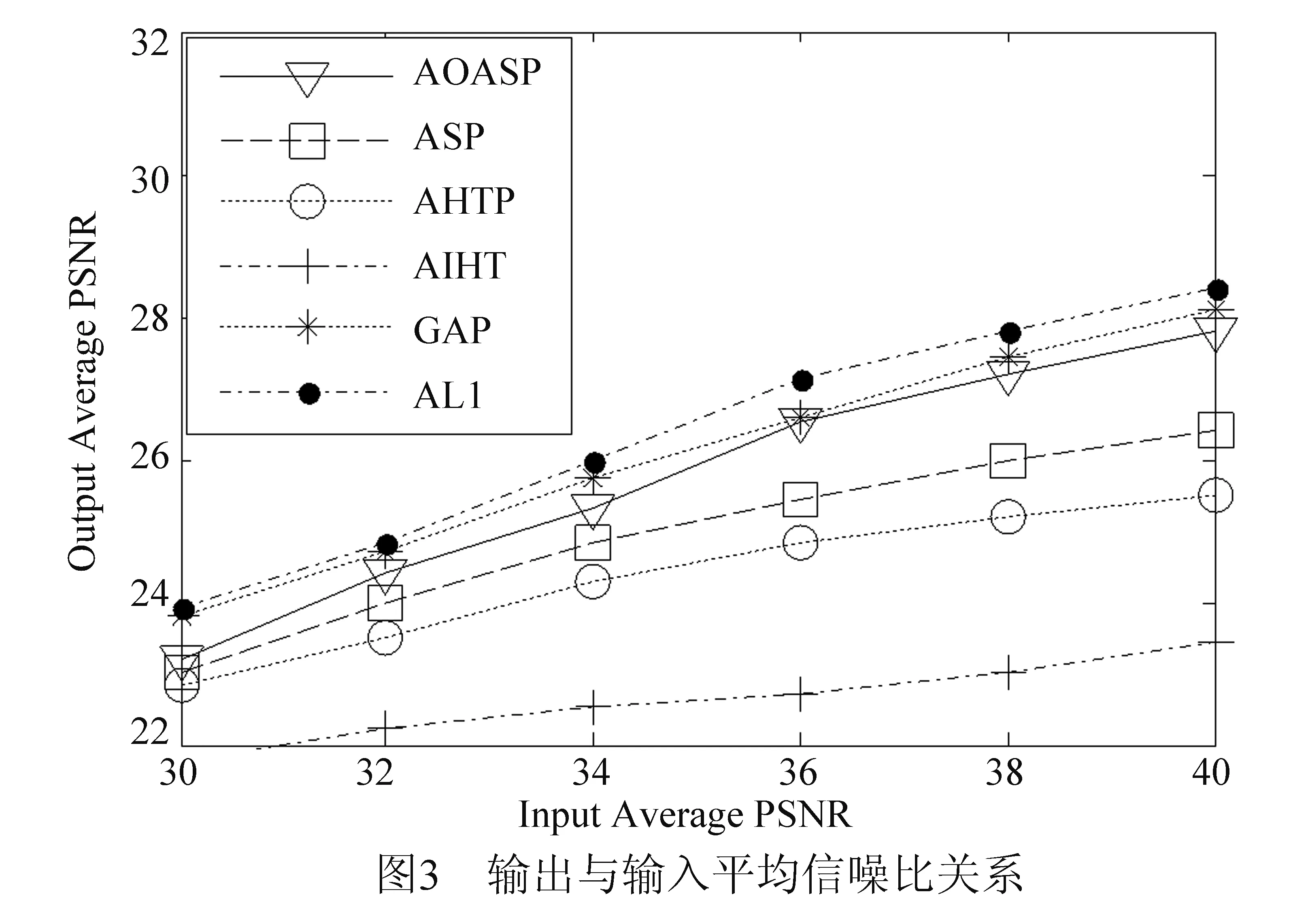
近年来,对压缩感知信号处理的研究一直十分活跃,其中一类约束优化问题是:从一组含有噪声的测量矢量y=Mx+e中重构原始信号矢量x∈Rd,其中测量矩阵M∈Rm×d(通常m 近十年来,国内外学者对稀疏综合模型下信号重构及其应用进行了深入研究,也取得了一系列成果[2-7],但是对稀疏补分析模型下信号优化研究还是近几年的事情,目前国内还没有这方面的文献报道.稀疏补分析模型下直接求解优化方程是一个NP-hard问题,故只能求近似最优解,方法有两类:一是采用分析l1范数法[9-10](Analysisl1Norm,AL1),该算法的完全重构概率很高、重构性能很好,但是算法计算量巨大、收敛速度慢.二是采用各种贪婪追踪策略,如:S.Nam在2013年提出贪婪分析追踪算法(Greedyanalysispursuit,GAP)[11],从一个满支撑集补开始追踪,每一次迭代去掉其中的一个元素,直到迭代满足终止条件为止,最后一次迭代的支撑集补就是最终解.此算法可以获得与AL1相当的重构性能,其不足之处是迭代需要遍历整个支撑集、计算量大、收敛速度也慢.2011年R.Giryes提出分析迭代硬阈值算法(AnalysisIterativeHardThresholding,AIHT)[12]把稀疏综合模型下的硬阈值跟踪[13]直接搬到稀疏补分析模型中来,也取得了不错的信号重构效果,但是没有考虑稀疏补分析模型下分析字典Ω和分析表示矢量Ωx的结构特点等问题,虽然收敛速度大大加快,但重构概率和重构性能较差.2012年R.Giryes把稀疏综合模型下硬阈值追踪[14]思想与AIHT算法相结合提出了稀疏补分析模型下的分析硬阈值追踪重构算法(AHTP)[15],与前几种算法相比,信号重构性能和收敛速度都有一定提升,但是并没有分析Ω的结构特点对算法性能的影响及算法收敛的保证条件等.2012年R.Giryes把稀疏综合模型下子空间追踪[16-17]类推到稀疏补分析模型中,提出分析子空间追踪(AnalysisSubspacePursuit,ASP)[18],与AIHT、AHTP做了对比,重构性能有一定提高,并给出了保证算法收敛的充分条件、重构误差上界.本文在ASP的基础上,根据不同分析字典的结构特点用近似目标优化函数取代原目标优化函数,改进了算法的迭代追踪步骤,对稀疏补的取值方法进行优化,提出了基于稀疏补分析模型的近似最优分析子空间追踪(ApproximateOptimalAnalysisSubspacePursuitbasedonCosparseAnalysisModel,AOASP),进一步提高了算法的完全重构概率和重构性能,并通过仿真实验证实了算法可行性. 定理3 对于任意Λ∈Ll,当且仅当||QΛ((I-M*M)QΛ)||2≤δl时,矩阵M满足Ω-RIP特性[15]. 3.1 AOASP算法介绍 步骤2,开始循环迭代i=i+1; 步骤6,扩充支撑集补Λi=cosupp(Ω,l); 3.2 AOASP算法性能分析 3.2.1 算法稳定重构条件 i=|log(||x||2/||e||2)/log(1/τρ1ρ2)|, C=1+((1-τρ1ρ2)i/(1-τρ1ρ2))(τ(η1+ρ1η2) +2(1-δ2l-p)), τ=(1+δ2l-p)/(1-δ2l-p),η1(i1+i2+i3),i1=(1+δ3l-2p)(γ(1+α)),i2=C2l-p(1+δ3l-2p)/(γ(1+γ)(1+α)), α, 定理5 给定随机矩阵M∈m×d,对于任意z∈d,常数CM>0,εl>0,如果成立,则δl≤εl将以大于1-e-t的概率成立. 对于Ω处于通用位置时,通常要求l 3.2.2 稀疏补l 选取方法 实验一,测试算法的完全重构概率.稀疏补运算符Ω采用随机紧支框架,测量矩阵M采用独立同分布构成的随机矩阵.δ=m/d表示亚取样率,ρ=(d-l)/m表示稀疏补与测量矢量数目的比值,也是Null(ΩΛ)的维数与测量数目的比值,ρ与δ的关系曲线称为相位过渡图.实验中m和l分别取20组不同值,即对应ρ和δ分别取不同的值,针对每一种取值组合,重复实验40次,测试各算法完全重构信号的概率.实验结果见图1,曲线下方表示对于ρ和δ不同取值,算法以100%的概率完全重构信号的情形,上方表示不能完全重构信号的情形.分析图中曲线可知,AOASP算法的信号完全重构概率明显高于ASP、AHTP、AIHT、GAP和AL1五种算法的完全重构概率.另外,曲线也说明了分析运算符Ω的冗余度越高,即Ω内向量的线性相关性越强,重构算法的性能越好. 实验二,测试算法的完全重构概率.稀疏补运算符Ω采用有限差分分析运算符ΩDIF,其它参数取值同实验一.实验结果仍然用相位过渡图表示,见图2.从图中可以看出,AOASP的信号完全重构概率明显高于ASP、AHTP、AIHT的信号完全重构概率. 通过对压缩感知信号优化问题中的稀疏补分析模型理论的研究,针对直接采用稀疏综合模型下子空间追踪过程非最速梯度下降和信号重构概率不高的缺点,引入稀疏补投影思想,根据稀疏补分析模型下分析字典的不同结构特点来设计近似目标优化函数,修正了迭代追踪过程,优化了稀疏补取值方法,设计并实现了基于稀疏补分析模型的近似最优分析子空间追踪算法,进一步提高了算法的完全重构概率,提高了算法的信号重构性能,通过仿真实验证实了算法是可行的.如何选择不同类型的分析字典Ω才能找到目标函数的近似最优解等需进一步研究. [1]Elad M,Milanfar P,Rubinstein R.Analysis versus synthesis in signal priors[J].Inverse Problems,2007,23 (3):947-968. [2]Candes E J,Eladar Y C,Needel D.Compressed sensing with coherent and redundant dictionaries[J].Applied and Computational Harmonic Analysis.2011,31 (1):59-73. [3]Rauhut H,Schnass K,Vanderhheynest P.Compressed sensing and redundant dictionaries[J].IEEE Trans.Inf.Theory.2008,54 (5):2210-2219. [4]Candes E J,Tao T.Near-optimal signal recovery from random projections:Universal encoding strategies?[J].IEEE Trans.On Inf.Theory,2006,52(12):5406-5425. [5]张宗念,黄仁泰,闫敬文.压缩感知盲稀疏度重构算法[J].电子学报,2011,39(1):18-21. Zhang Zong-nian,Huang Ren-tai,Yan Jing-wen.A Blind Sparsity Reconstruction Algorithm for Compressed Sensing Signal[J].Acta Electronica Sinica,2011,39(1):18-21.(in Chinese) [6]练秋生,陈书贞.基于解析轮廓波变换的图像稀疏表示及其在压缩传感中的应用[J].电子学报,2010,38(6):1-6. Lian Qiu-sheng,Chen Shu-zhen.Sparse image representation using the analytic contourlet transform and its application on compressed sensing[J].Acta Electronica Sinica,2010,38(6):1-6.(in Chinese) [7]Foucart S.Sparse recovery algorithms:sufficient conditions in terms of restricted isometry constants[C].Approximation Theory XIII,Springer Proceedings in Mathematics,2010,65-77. [8]Garg R,Khandekar R.Gradient descent with sparsication:an iterative algorithm for sparse recovery with restricted isometry property[A].Proceedings of the 26th Annual International Conference on Machine Learning,ICML ′09[C].ACM,New York,NY,USA,2009,337-344. [9]Cai J,Osher S,Shen Z.Split bregman methods and frame based image restoration[J].Multiscale Modeling & Simulation,2009,8(2):337-369. [10]Dai W,Milenkovic O.Subspace pursuit for compressive sensing signal reconstruction[J].IEEE Transactions on Information Theory,2009,55(5):2230-2249. [11]Nam S,Davis M,Elad M,et al.The cosparse analysis model and algorithms[J].Applied and Computational Harmonic Analysis.2013,34(1):30-56. [12]Giryes R,Nam S,Gribonval R.Iterative cosparse projection algorithms for the recovery of cosparse vectors[A].The 19thEuropean Signal Processing Conference (EUSIPCO-2011)[C],Barcelona,Spain,2011. [13]Blumensath T,Davis M.Iterative hard thresholding for compressed sensing[J].Applied and Computational Harmonic Analysis,2009,27 (3):265-274. [14]FoucartS S.Hard thresholding pursuit:an algorithm for compressive sensing[J].SIAM J.Numer.Anal.2011,49 (6):2543-2563. [15]Giryes R,Nam S,Elad M.Greedy-like algorithm for the cosparse analysis model[J].Special Issue in LAA on Sparse Approximate solution of Linear Systems.2012,(7). [16]Lu Y M,Do M N.A theory for sampling signals from a union of subspaces[J].IEEE Trans.Signal Process.,2008,56(6):2334-2345. [17]Blumensath T,Davies E.Sampling theorems for signals from the union of finite-dimensional linear subspaces[J].IEEE Trans.Inform.Theory,2009,55(4):1872-1882. [18]Giryes R,Nam S,Elad M.CoSamp and SP for the cosparse analysis model[A].20thEuropean Signal Processing Conference(EUSIPCO 2012)[C].Bucharest,Romania,Aug,2012.26-31. [19]Nam S,Davis M,Elad M,et al.Cosparse analysis modeling[A].The 9th International Conference on Sampling Theory and Applications(sampta-2011)[C].Singapore,2011. 张宗念 男,1963年6月生于河北深州,副教授.2000年获华南理工大学博士学位.主要研究方向为压缩感知理论与应用、图像处理. E-mail:zzn99@sohu.com 李金徽 男,1980年4月生于辽宁沈阳,工程师.2004年获重庆工商大学学士学位.主要研究方向为分布式计算机网络. E-mail:li@dgut.edu.cn 黄仁泰 男,1964年12月生于广东东莞,副教授.2006年获华中科技大学硕士学位.主要研究方向为分布式计算机网络. E-mail:huangrt@dgut.edu.cn 闫敬文 男,1964年7月生于吉林磐石,博士,教授,博士生导师.1997获中国科学院长春光机所博士学位.主要研究方向为图像处理和分析、遥感图像处理等. E-mail:jwyan@stu.edu.cn Approximately Optimal Subspace Pursuit Based on Cosparse Analysis Model ZHANG Zong-nian1,LI Jin-hui2,HUANG Ren-tai3,YAN Jing-wen4 (1,DepartmentofElectronicEngineering,DongguanUniversityofTechnology,Dongguan,Guangdong523808,China;2.NetworkCenter,DongguanUniversityofTechnology,Dongguan,Guangdong523808,China;3.DepartmentofComputerScience,DongguanUniversityofTechnology,Dongguan,Guangdong523808,China;4.DepartmentofElectronicsEngineering,ShantouUniversity,Shantou,Guangdong515063,China) An approximately optimal subspace pursuit algorithm under cosparse analysis model was studied to reconstruct the original signal from the noisy measurement vectors.To overcome the drawbacks of the non steepest gradient during the pursuit process and the low successful reconstruction probability for sparse synthesis model,an approximately optimal subspace pursuit algorithm based on cosparse analysis model was presented and realized.The approximately optimal optimization object function for the algorithm was designed according to the structure of the different analysis dictionaries,the iterative pursuit process of the algorithm was revised,and the methods of selecting cosparsity was optimized.The simulation experiments show that the complete reconstruction probability of the new algorithm is evidently larger than that of the algorithm for ASP,AHTP,AIHT,AL1 and GAP when the cosparse operator is a random compact frame or a two dimension total variant matrix.The comprehensive average PSNR of the output signal for the new algorithm is larger than that of the algorithm of ASP,AHTP,and AIHT for 0.8dB,1.38dB and 3.13 dB respectively and is less than that of the algorithm of GAP and AL1 for 0.32 dB and 0.6dB when the input signal is with Gaussion noise.The complete reconstruction probability of the new algorithm was greatly improved by adopting the above measures,and the convergence condition for the new algorithm was simplified. cosparse analysis model;approximately optimal;subspace;pursuit 2013-01-18; 2016-03-04; 责任编辑:郭游 国家自然科学基金(No.40971206);广东省自然科学基金(No.2015A030313654) TN911.72 A 0372-2112 (2016)10-2289-05 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.10.001
2 稀疏补分析模型
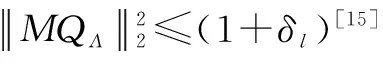
3 近似最优分析子空间追踪算法
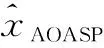
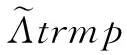

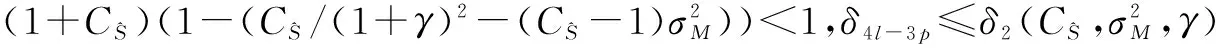
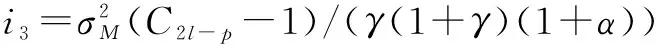
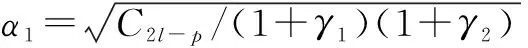
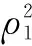
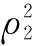
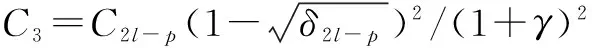
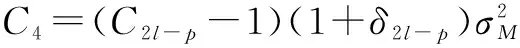
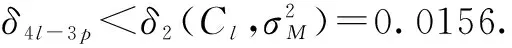
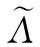
4 仿真实验
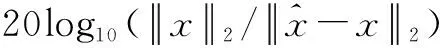
5 结论





