循环荷载作用下心墙掺砾土动应力应变孔压模型
聂 章 博, 迟 世 春*
( 1.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024;2.大连理工大学 水利工程学院 工程抗震研究所, 辽宁 大连 116024 )
循环荷载作用下心墙掺砾土动应力应变孔压模型
聂 章 博1,2, 迟 世 春*1,2
( 1.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024;2.大连理工大学 水利工程学院 工程抗震研究所, 辽宁 大连 116024 )
动力荷载作用下,心墙掺砾土的累积塑性变形和孔隙水压力的发展对心墙防渗体的安全至关重要.基于Bouc-Wen光滑滞回模型,考虑滞回圈捏拢效应,结合非关联流动法则,建立本构模型,模拟循环过程中土体产生的累积塑性应变和增长的孔压.通过糯扎渡心墙掺砾土均压固结和偏压固结状态的循环三轴试验,研究其动应力应变关系及孔压响应.将模型曲线与试验曲线进行对比分析,验证模型描述掺砾土动应力应变关系的合理性和有效性.
心墙掺砾土;循环荷载; Bouc-Wen模型;累积塑性应变;孔压
0 引 言
高土石坝采用砾石与黏性土混合后的改性掺砾土作为心墙筑坝料在实际工程中应用日益增多,取得了很好的效果[1].掺入砾石料可显著提高心墙防渗体的变形模量,使得防渗体与坝壳料的变形更为协调,有效减少了心墙与上下游堆石坝料的不均匀变形和拱效应,降低心墙裂缝的发生概率,防止心墙水力劈裂现象的发生.试验研究与工程实践表明含砾量30%~40%,其压实密度、渗透性能、压缩性能及抗剪强度等工程特性可满足实际工程需要.掺砾土既包含黏土又包含粗粒土,其动力特性复杂,尤其是累积变形特性和动孔压有待进一步研究.
目前,通常采用等效黏弹性模型或弹塑性模型研究土体动力特性.等效黏弹性模型在实际工程中应用广泛,但难以计算永久变形、动孔压等土体重要动力特性.蔡袁强等将软化指数经验模型引入Iwan模型模拟黏土应变软化特性,并通过再串联理想刚塑性元件模拟循环过程中产生的累积塑性应变[2].黄茂松等考虑围压及偏应力水平的影响,采用显式模型计算循环荷载下饱和软黏土轴向累积应变[3].弹塑性模型中边界面模型取消多重嵌套的屈服面,采用一套映射准则和插值函数计算塑性模量,但其理论推导复杂.刘方成等将阻尼比的影响引入土体塑性硬化模量,反映土的阻尼比对动力响应的影响[4].胡存等研究饱和黏土各向异性对其后继循环特性的影响,建立循环边界面塑性模型[5].李剑等对边界面模型进行改进,考虑加卸载过程中黏土的弹塑性特性,引入边界面胀缩规则,反映黏土的滞回特性[6].Papadimitriou 等学者应用边界面模型研究多轴应力空间土体动力特性,并引入结构演化因子对塑性模量的影响[7].Gerolymos和Drosos等学者曾将Bouc-Wen模型应用于土体,描述各种不同土体的非线性滞回性、刚度退化和孔隙水压力升高引起的强度丧失,以及循环流动性和荷载引起的各向异性等[8-9].
本文基于Bouc-Wen光滑滞回模型,引入非关联流动法则,建立能够考虑刚度退化及累积塑性变形和动孔压的掺砾土动应力应变孔压模型.应用GDS动三轴仪进行应力控制式循环三轴试验,分析糯扎渡心墙掺砾土均压、偏压固结的应力应变关系、轴向累积塑性变形及孔压发展形态.最后将模型计算曲线与试验曲线进行比较,验证模型的合理性和有效性.
1 本构模型简述
Bouc-Wen光滑滞回模型描述形态各异的应力应变滞回圈,剪应力τ与剪应变γ关系如下:
τ=τyz
(1)
式中:τy是土体剪切强度;z是滞回参量,可由以下微分方程得出:

z.=1ηγ.γy(1-(b+(1-b)sgn(γ.z))
zn)
(2)
式中:b、n是滞回圈形状系数;γy=τy/Gmax,是参考剪应变;Gmax是初始最大弹性模量;刚度退化系数η=1+η0δ,是累积滞回耗能δ的线性函数;η0是量纲一的参数.土体在时程t内单位累积滞回耗能

δ=τy∫t0zγ.dt
(3)
强震荷载作用下土体结构产生裂缝、破碎或滑移,表现为循环流动性,使得土体在较小动应力水平切线刚度降低,发生相对较大的塑性应变,其应力应变滞回圈在平衡位置附近表现明显的收缩现象,即滞回圈捏拢效应[10],引入参量λ,有

λ=1-λ1(1-exp(-λ2δ))exp(-(zsgn(γ.)λ3γ)2)
(4)
其中λ1、λ2、λ3是控制滞回圈捏拢效应的参数.λ1是控制应力应变滞回圈在坐标轴附近收缩程度的量纲一的参数,λ2控制累积耗能对捏拢效应的影响,λ3控制当前剪应变对捏拢效应的影响.滞回参量z的微分方程式(2)修正为

z.=ληγ.γy(1-(b+(1-b)sgn(γ.z))
zn)
(5)
令式(5)等于零,可得滞回参量z的极值zmax=1.考虑应力反向,若令
(6)
其中zr是先前应力反向时滞回参量z的最大值,则硬化参量ζ可表征应力空间中当前应力状态,有
(7)
其中p、q分别是偏应力和有效球应力;Mcs是p-q应力空间临界状态线斜率,与残余内摩擦角φcs相关.硬化参量ζ=1,土体趋于临界状态.引入塑性流动法则,即
(8)

Mpt=Mcs+(Mpt0-Mcs)exp-w∑dγ
(9)
其中Mpt0是相变转换线斜率初值,w是模型参数.土体从剪缩过渡到剪胀时,应力比等于Mpt,塑性体变增量等于零;土体趋于临界状态时,相变转换线收敛于临界状态线,硬化参量ζ=1,塑性体变增量趋于零.
Byrne等提出不排水条件孔压与排水塑性体变的增量关系[12]:
(10)
式中:np是土体的孔隙率;Ke和Kf分别是土骨架与孔隙流体的体积模量,由下式确定:
(11)
(12)
式中:ν是泊松比,Kf依赖于有效固结应力p0以及初始饱和度Sr0,pa是标准大气压力.初始饱和度越高,孔隙流体刚度越大,塑性体变增量引起的孔压增量越大.
2 模型验证
为验证模型的合理性,本文对糯扎渡心墙掺砾土进行循环三轴试验,编制计算程序,对掺砾土应力应变关系进行模拟.
2.1 掺砾土循环三轴试验
试验在GDS动三轴仪上进行,采用应力控制加载方式,加载波形由伺服系统生成,选用正弦波.振动频率为0.1 Hz,土样直径100 mm,高200 mm.试验材料为糯扎渡心墙掺砾土,其中黏土样相对密度Gs=2.71,液限ωl=27.0%,塑限ωp=15.3%,塑性指数Ip=11.7%.掺砾土所用砾石不均匀系数Cu=7.23,曲率系数Cc=1.97,其级配情况见表1.
掺砾土制样干密度ρd=1.96 g/cm3, 其中砾石质量占35%,试样的最优含水率为14.86%,孔隙率np=0.26,泊松比ν=0.33.掺砾土不排水循环三轴试验条件及破坏振次见表2.


2.2 本构模型参数
模型各参数可根据不同的试验数据确定,其中滞回圈形状参数需根据动模量阻尼试验得到的滞回圈进行数值反演校正.弹性模量参数由动模量阻尼试验测得,静力有效强度指标由静力不排水三轴压缩试验测得,相变转换状态参数与临界状态参数由三轴压缩排水试验相应状态内摩擦角确定.
剪切强度τy可由摩尔-库仑准则确定:
τy=c+σtanφ
(13)
其中c、φ是静力有效强度指标,可由静力不排水三轴压缩试验得到.
弹性剪切模量可由动模量阻尼试验确定:
(14)
式中:σm=(σ1+2σ3)/3,是平均有效应力;k和m可通过整理不同围压的归一化弹性剪切模量lg(Gmax/pa) 与平均应力lg(σm/pa)在双对数坐标中的试验数据得到,二者近似呈直线关系,其纵轴截距为k,斜率为m.
相变转换状态应力比初值Mpt0和临界状态应力比Mcs可分别由下式求得:
(15)
(16)
其中φpt0是土体在三轴压缩排水试验由剪缩到剪胀相变转换时的内摩擦角;φcs是土体达到临界状态时的残余内摩擦角.整理三轴压缩排水试验不同应变水平应力比与累积剪应变的关系,可测得式(9)中模型参数w.
整理心墙掺砾土各试验数据,得到模型参数,统计如表3所示.

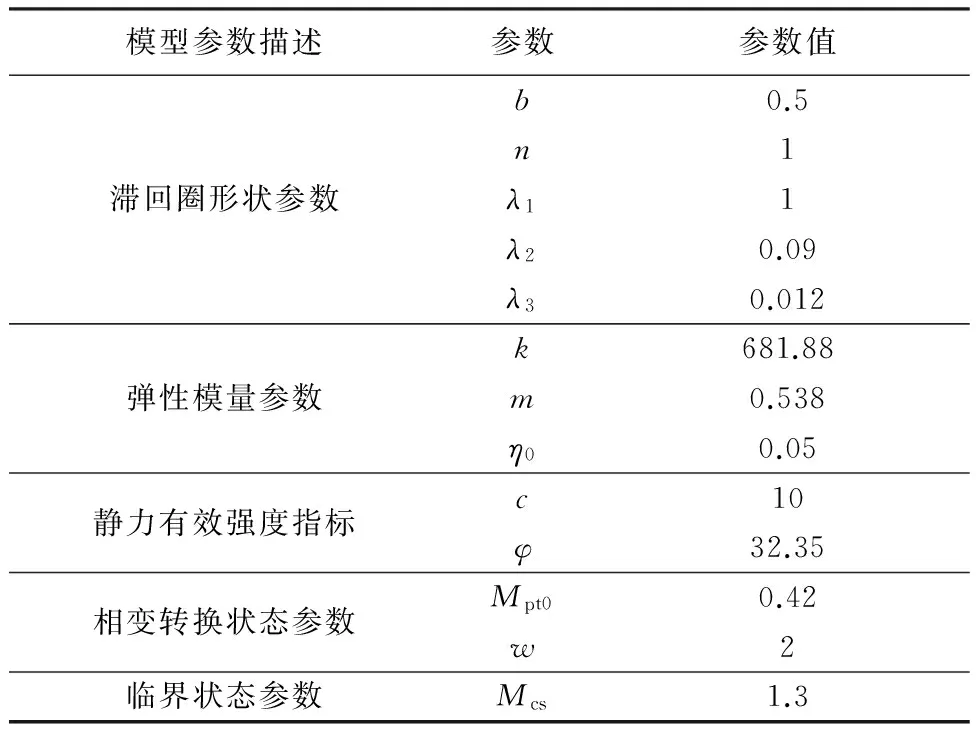
表3 数值模拟参数
2.3 模拟结果
本文根据以上参数,对掺砾土p0=200 kPa不同固结条件应力控制式动三轴试验进行模拟,并将计算的动剪应力应变τ-γ关系转换为轴向偏应力应变q-ε1关系,结果见图1~6.
图1是掺砾土均压固结轴向应变时程曲线.如图1(a)所示,在循环荷载作用下振动初期(N<10)应变振幅增长缓慢,但随着振次增加,应变振幅有增大的趋势,振次N>20以后,应变振幅急剧增大,振次N=40时双幅应变达到5%.应变试验曲线随着振次增加逐渐偏向拉伸侧,表明掺砾土承受动力荷载具有拉压不等性.图1(b)中本文Bouc-Wen模型计算曲线能较好模拟上述心墙掺砾土应变发展特性,但模型计算曲线拉压侧应变幅值对称,未能表现拉压不等性,N=40时双幅应变达到4.68%.


(a) 试验曲线

(b) 本文Bouc-Wen模型计算曲线
(Kc=1.0,p0=200 kPa,σd=120 kPa)
图1 均压固结轴向应变时程曲线
Fig.1 Time history curves of axial strain with isotropic consolidation
图2(a)是掺砾土循环三轴试验应力应变滞回圈.心墙掺砾土在循环荷载作用下将产生应变软化.振次越大,掺砾土的割线刚度越小.一个振动周期内,加载阶段低应力水平压缩模量衰减较快,拉压侧循环累积应变增长较快;卸载阶段掺砾土刚度较大,土体变形较小.图2(b)是根据文献[7]边界面模型计算得到的应力应变滞回圈,图2(c) 是本文Bouc-Wen模型计算的滞回圈.文献[7]模型计算曲线能够描述掺砾土应变幅值随振次增加而增大的应变软化现象,但其应力应变曲线不光滑,且随着振次增加,应变振幅增长较快,较少振次即达到破坏振次,与实测值拟合效果较差.本文修正Bouc-Wen模型能够反映滞回圈在横轴附近收缩的捏拢效应,其应力应变曲线形状及光滑度与实测值较为相符,达到破坏应变所需振次也与实测振次较为接近.


(a) 试验曲线

(b) 文献[7]模型计算曲线

(c) 本文Bouc-Wen模型计算曲线
(Kc=1.0,p0=200 kPa,σd=120 kPa)
图2 均压固结应力应变滞回圈
Fig.2 Stress-strain hysteresis loops with isotropic consolidation
图3是掺砾土不排水循环三轴孔压时程曲线,孔压比ru=Δu/p0.初始饱和度较高,均压固结下孔压升高较快,但心墙掺砾土渗透性小,孔压传递较慢,振次N>20以后,孔压趋于稳定.孔压幅值较大,卸载再加载过程孔压波动较大,使得土骨架受到的有效应力变化较大,促进了应变软化及刚度退化.
如图4所示,由于存在初始偏应力,随着振次增大, 应变时程曲线逐渐向压缩侧偏移,累积塑性应变均为压应变.应变幅值随振次增加而增大,表现出刚度退化效应.


(a) 试验曲线

(b) 本文Bouc-Wen模型计算曲线

(Kc=1.0, p0=200 kPa, σd=120 kPa)

(a) 试验曲线

(b) 本文Bouc-Wen模型计算曲线
(Kc=1.5,p0=200 kPa,σd=180 kPa)
图4 偏压固结轴向应变时程曲线
Fig.4 Time history curves of axial strain with anisotropic consolidation
图5是掺砾土偏压固结应力应变滞回圈试验值与模型计算值.如图5(a)所示,由于初始偏应力的存在,心墙掺砾土在循环荷载作用下振动压密,滞回圈向右侧偏移.图5(b)是根据文献[7]模型计算得到的滞回圈,该模型能够表现滞回圈随循环振次增加向右侧偏移的趋势,但模拟滞回圈面积较小,易低估心墙掺砾土阻尼耗能.图5(c)是本文Bouc-Wen模型计算得到的滞回圈.与图5(b) 相比,本文模型克服了上述缺陷,能够较好地模拟掺砾土应力应变关系曲线的动力特性.


(a) 试验曲线

(b) 文献[7]模型计算曲线
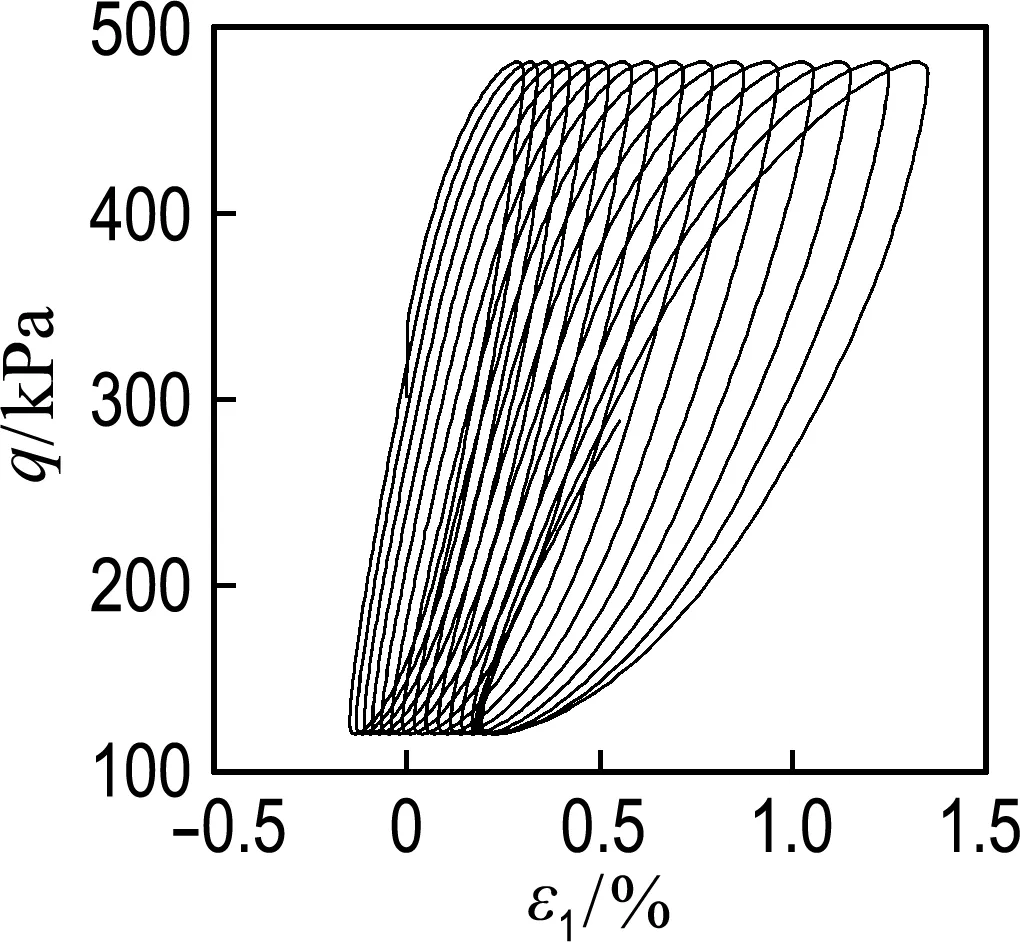
(c) 本文Bouc-Wen模型计算曲线
(Kc=1.5,p0=200 kPa,σd=180 kPa)
图5 偏压固结应力应变滞回圈
Fig.5 Stress-strain hysteresis loops with anisotropic consolidation
相对于均压固结时孔压时程曲线(图3),图6所示偏压固结孔压随循环振次增加而增长较慢,并且卸载再加载过程中,波动孔压幅值较小,表明初始偏应力抑制孔压的发展.


(a) 试验曲线

(b) 本文Bouc-Wen模型计算曲线
(Kc=1.5,p0=200 kPa,σd=180 kPa)
图6 偏压固结孔压时程曲线
Fig.6 Time history curves of pore water pressure with anisotropic consolidation
3 结 论
(1)循环荷载作用下,心墙掺砾土中孔隙水压力随着循环振次增加而不断增大,土体的有效围压不断减小造成土体软化.掺砾土中黏土颗粒与砾石间摩擦咬合力和黏聚力随着振次增加而降低,刚度退化,同时土颗粒重排,孔隙有减少的趋势,土体产生累积塑性变形.均压固结时,卸载再加载过程中有效应力变化较大,刚度退化明显,拉压侧应变幅值增长较快;偏压固结时,土体始终承受压应力,轴向累积应变向压缩侧累积,滞回圈随振次增加向右侧偏移.
(2)振动开始时心墙掺砾土孔压升高较快,随着振次的逐渐增加,动孔隙水压力逐渐增大并趋于稳定.均压固结时,波动孔压幅值较大,最终孔压比ru峰值接近0.9;偏压固结时,初始偏应力的存在抑制孔压的发展,其增长速率及波动幅值均较均压固结时偏小.
(3)本文所提本构模型能较好反映上述心墙掺砾土累积变形及孔压发展特性.循环荷载次数较大时,累积应变增长量预测值与实测值仍能较好吻合.与边界面模型相比,Bouc-Wen模型应力应变滞回圈光滑度更好,模拟掺砾土阻尼耗能更精确.
[1] 张宗亮,冯业林,相 彪,等. 糯扎渡心墙堆石坝防渗土料的设计、研究与实践[J]. 岩土工程学报, 2013, 35(7):1323-1327.
ZHANG Zong-liang, FENG Ye-lin, XIANG Biao,etal. Design, researches and practices of impervious materials for core wall of Nuozhadu Hydropower Station [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(7):1323-1327. (in Chinese)
[2] 蔡袁强,柳 伟,徐长节,等. 基于修正Iwan模型的软黏土动应力-应变关系研究[J]. 岩土工程学报, 2007, 29(9):1314-1319.
CAI Yuan-qiang, LIU Wei, XU Chang-jie,etal. Study on dynamic stress-strain relationship of soft clay based on modified Iwan′s model under undrained cyclic loading [J]. Chinese Journal of Geotechnical Engineering, 2007, 29(9):1314-1319. (in Chinese)
[3] 黄茂松,姚兆明. 循环荷载下饱和软黏土的累积变形显式模型[J]. 岩土工程学报, 2011, 33(3):325-331.
HUANG Mao-song, YAO Zhao-ming. Explicit model for cumulative strain of saturated clay subjected to cyclic loading [J]. Chinese Journal of Geotechnical Engineering, 2011, 33(3):325-331. (in Chinese)
[4] 刘方成,尚守平,王海东,等. 基于阻尼的边界面模型[J]. 岩土工程学报, 2009, 31(6):851-858.
LIU Fang-cheng, SHANG Shou-ping, WANG Hai-dong,etal. Damping ratio-based bounding surface model [J]. Chinese Journal of Geotechnical Engineering, 2009, 31(6):851-858. (in Chinese)
[5] 胡 存,刘海笑. 考虑饱和黏土初始各向异性的循环边界面塑性模型[J]. 岩土力学, 2014, 35(10):2807-2814, 2830.
HU Cun, LIU Hai-xiao. A cyclic bounding surface plasticity model for saturated clay with initial anisotropy [J]. Rock and Soil Mechanics, 2014, 35(10):2807-2814, 2830. (in Chinese)
[6] 李 剑,陈善雄,姜领发. 循环荷载作用下黏土改进边界面模型[J]. 岩土力学, 2015, 36(2):387-392, 450.
LI Jian, CHEN Shan-xiong, JIANG Ling-fa. An improved bounding surface model for clay under cyclic loading [J]. Rock and Soil Mechanics, 2015, 36(2):387-392, 450. (in Chinese)
[7] Papadimitriou A G, Bouckovalas G D. Plasticity model for sand under small and large cyclic strains:a multiaxial formulation [J]. Soil Dynamics and Earthquake Engineering, 2002, 22(3):191-204.
[8] Gerolymos N, Gazetas G. Constitutive model for 1-D cyclic soil behaviour applied to seismic analysis of layered deposits [J]. Soils and Foundations, 2005, 45(3):147-159.
[9] Drosos V A, Gerolymos N, Gazetas G. Constitutive model for soil amplification of ground shaking:Parameter calibration, comparisons, validation [J]. Soil Dynamics and Earthquake Engineering, 2012, 42:255-274.
[10] 余 波,洪汉平,杨绿峰. 非弹性体系地震动力响应分析的新型单轴Bouc-Wen模型[J]. 工程力学, 2012, 29(12):265-273.
YU Bo, HONG Han-ping, YANG Lu-feng. Improved uniaxial Bouc-Wen model for seismic dynamic response analysis of inelastic system [J]. Engineering Mechanics, 2012, 29(12):265-273. (in Chinese)
[11] Tasiopoulou P, Gerolymos N. Constitutive modeling of sand:Formulation of a new plasticity approach [J]. Soil Dynamics and Earthquake Engineering, 2016, 82:205-221.
[12] Byrne P M, Park S S, Beaty M H,etal. Numerical modeling of liquefaction and comparison with centrifuge tests [J]. Canadian Geotechnical Journal, 2004, 41(2):193-211.
Dynamic stress-strain pore water pressure model of core gravelly soil under cyclic loading
NIE Zhang-bo1,2, CHI Shi-chun*1,2
( 1.State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China;2.Institute of Earthquake Engineering, School of Hydraulic Engineering, Dalian University of Technology,Dalian 116024, China )
Cumulative plastic deformation and development of the pore water pressure occurred in core gravelly soil under dynamic loading are of most importance for security of impervious core of dam. Based on Bouc-Wen smooth hysteretic model, considering hysteretic loop pinching effect and non-associative flow rule, a constitutive model is proposed to describe cumulative plastic strain and increasing pore water pressure of soil subjected to cyclic loading. Cyclic triaxial tests for Nuozhadu′s core gravelly soil under isotropic and anisotropic stress conditions have been carried out and dynamic stress-strain relationship and pore water pressure response are analyzed. By comparing the experimental and simulated curves, the presented model is proved to be reasonable and effective for describing dynamic stress-strain relationship of gravelly soil.
core gravelly soil; cyclic loading; Bouc-Wen model; cumulative plastic strain; pore water pressure
2016-04-17;
2016-09-06.
国家自然科学基金资助项目(51179024,51379029).
聂章博(1986-),男,博士生,E-mail:niezhangbo_0809@163.com;迟世春*(1964-),男,教授,博士生导师,E-mail:schchi@dlut.edu.cn.
1000-8608(2016)06-0624-07
TU435
A
10.7511/dllgxb201606010
——结构相互作用的影响分析

