基于赫巴流体的页岩气大位移水平井裸眼延伸极限分析

李 鑫 高德利 刁斌斌 周英操

1.中国石油大学石油工程教育部重点实验室 2.中国石油集团钻井工程技术研究院

基于赫巴流体的页岩气大位移水平井裸眼延伸极限分析

李 鑫1高德利1刁斌斌1周英操2

1.中国石油大学石油工程教育部重点实验室 2.中国石油集团钻井工程技术研究院

李鑫等.基于赫巴流体的页岩气大位移水平井裸眼延伸极限分析.天然气工业，2016, 36(10): 85-92.

大位移水平井的裸眼延伸极限主要与环空压耗和地层破裂压力等因素有关，不同的钻井液流变模式又会对环空压耗的描述产生较大的影响，而赫巴模式能够更好地模拟实际钻井液的流变特性。为此，建立了基于赫巴流体的页岩气储层大位移水平井裸眼延伸极限模型，进而用实际案例分析了赫巴流体的基本流变参数（流性指数、稠度系数、屈服值）和主要钻进参数（机械钻速、钻井液密度、钻杆转速）对大位移水平井水平段延伸极限的影响，并将其与幂律流体模型计算结果进行对比分析。结果表明：①在同样的条件下，采用赫巴流体所得结果小于采用幂律流体计算的结果，新预测模型可靠性更好；②通过参数的敏感性分析可知，水平段延伸极限会随着上述3个基本流变参数和机械钻速的增加而减小，而该极限值会随着钻井液密度的增加而先增加后减小，它也会随着钻杆转速的增加而增加。结论认为：所给出的赫巴流体流变参数和钻进参数的优选方法，有助于解决大位移水平井在页岩储层中究竟可以打多远的问题，并且更加精确地预测了其裸眼延伸极限。

页岩气 水平井大位移钻井 赫巴流体 裸眼延伸极限 流变参数 钻进参数 优选方法

我国页岩油气资源丰富，其高效开发有利于改善我国的能源结构[1-4]。水平井，尤其是大位移水平井已成为开采我国页岩气资源的关键技术手段之一[5-9]，可大幅度提高单井产量及综合开发效益[10-11]，如美国在2000年以后逐渐采用大位移水平井来代替直井进行页岩气的开发，取得了很好的开发效果[12]。一般来说，大位移水平井的水平段越长其产量也越高。随着钻井技术的不断进步，大位移水平井得到了越来越多的应用，其最大测深也不断创造出新的世界纪录[13-14]。大位移水平井究竟可以打多远，已经成为人们普遍关心的核心问题之一，而裸眼延伸极限原理就可以用来解释这一问题。

2006年，覃成锦等[15]指出，大斜度井最容易在测深最大处压破地层，通过研究大斜度井裸眼井段的安全密度窗口和环空循环压耗之间的关系，得到了套管最大下深的计算公式。2009年，高德利等[16]首次提出了大位移井裸眼延伸极限的概念和原理，并建立了相应的预测模型。高德利还将大位移井的延伸极限分为3种，包括裸眼延伸极限、水力延伸极限以及机械延伸极限，分别对应裸眼的井壁稳定延伸极限、水利工程的延伸极限和机械装备的延伸极限。裸眼延伸极限主要是指在大位移井的裸眼井段发生破裂时的最大井眼长度，它主要与环空压耗和地层破裂压力相关；水力延伸极限是指在一定的制约条件下，大位移井所能达到的极限测深，这里的制约条件主要是指泥浆泵等水力设备的能力，和钻井水力参数、钻速等相关；机械延伸极限主要是指在钻井系统机械性能上可以保证安全钻达的最大井深，主要包括钻柱的钻进极限和套管柱的下入极限，它们和作业工况、管柱的摩阻扭矩，管柱强度、钻机负荷等相关[16]。本文研究的主要是其中的裸眼延伸极限。2013年，孙腾飞等[17]对大位移井裸眼延伸极限模型做了进一步的发展，本质在于细化了当量循环密度（ECD）的计算过程，使计算结果更为精确可信。2013年，罗伟等[18]针对一口已钻大位移井进行实例分析，研究了其裸眼井段的延伸能力。笔者也建立了大位移水平井裸眼延伸极限的预测模型，并成功地将该模型应用于山地页岩气开发和海洋大位移钻井中，还利用裸眼延伸极限原理对传统的安全密度窗口进行了修正，取得了良好的效果。

大位移水平井的裸眼延伸极限主要与环空压耗和地层破裂压力等因素有关，而不同的钻井液流变模式又会对环空压耗的描述产生较大的影响。上述模型均是在钻井液采用幂律模式的情况下建立的，虽然幂律模式被广泛用于描述钻井液的流变性能，但是研究表明，在常规钻井液流变模式(宾汉、幂律和赫巴模式)中，宾汉模式和幂律模式都有其局限性，而赫巴模式能够更好地模拟实际钻井液的流变特性[19]。具体来说，赫巴模式的准确性最高[20]，实验也表明它的参数拟合优度最大[21]，总体误差也最小[22]。因此有必要建立基于赫巴模式钻井液的大位移水平井裸眼延伸极限模型，并分析赫巴模式钻井液的流变参数和主要钻进参数对其裸眼延伸极限的影响，随后将研究结果与采用幂律模式流体进行研究时所得到的结果进行比较分析，以减少采用幂律模式流体进行建模分析时所带来的与实际钻井中存在的误差和可能引起的钻井安全事故。本文将从大位移水平井的裸眼延伸极限原理出发，建立基于赫巴流体的页岩气储层大位移水平井裸眼延伸极限模型，并考察其主要流变参数（屈服值、流性指数、稠度系数）和常规钻进参数（机械钻速、钻井液密度、钻杆转速）的变化对大位移水平井裸眼延伸极限尤其是水平段延伸极限的影响，并筛选出最优的钻井液流变参数和钻进参数，以期达到提高大位移水平井在页岩储层中的延伸能力并提高页岩气产量的目的。

1 裸眼延伸极限预测模型

大位移水平井裸眼延伸极限原理可以用来解决大位移水平井究竟可以打多远的问题。其基本原理是：大位移水平井的水平段不能无限制的延伸，当其井底压力与地层破裂压力相等时地层就会被压破，即大位移井在钻进时存在一个临界点，此时水平段的长度被称为大位移水平井的水平段延伸极限，而整个井眼的测深就被称为大位移水平井的裸眼延伸极限。它们的值主要取决于钻井液循环时所产生的环空压耗以及所钻地层的破裂压力。基于上述原理，笔者建立了大位移水平井裸眼延伸极限的预测模型，重点在于预测水平段的延伸极限长度，推导过程如下：

当大位移水平井的井斜角接近或者达到90°并进入水平段钻进后，地层的破裂压力当量密度可以认为保持不变，当井底压力等于地层的破裂压力时大位移水平井便停止延伸。因此大位移水平井不能无限制延伸，它存在一个临界点。此临界点的情况可以表示如下[15-16,23]：

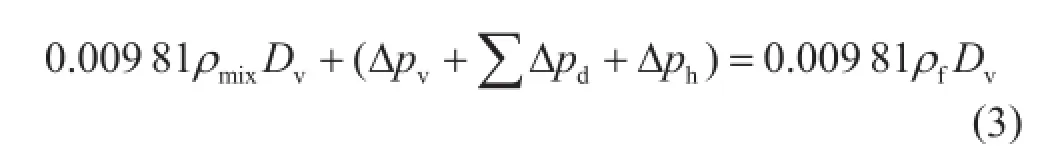
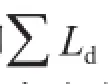
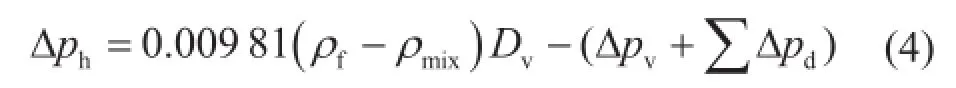
如果水平段的环空压耗梯度(Δp/ΔL)h也可以确定，那么水平段的延伸极限长度Lh就可以由式进行确定：

式中Lh表示水平段延伸极限，m；(Δp/ΔL)h表示水平段的环空压耗梯度，MPa/m。

再将式代入式可以得到：

而整个大位移水平井的裸眼延伸极限（Lt）可以由式进行确定：

从式（6）和式（7）可以看出，水平段延伸极限值（Lh）是预测大位移水平井裸眼延伸极限（Lt）的关键所在，而Lh又与各井段的环空压耗以及钻遇水平段地层的破裂压力密切相关，而不同流变模式的钻井液其循环时所产生的环空压耗也有所差别。

2 预测模型的求解

2.1 环空压耗计算

从公式（6）可以看出，对于某一确定垂深（Dv）的大位移水平井来说，其在水平段钻遇地层的破裂压力当量密度（ρf）以及所使用的钻井液密度（ρm）都可以认为是已知的。因此水平井裸眼延伸极限的计算转化为计算上层各井段的环空压耗以及水平段的环空压耗梯度的问题。为了方便建立模型和参数敏感性分析的需要，首先进行如下假设：

1）本文采用针对页岩气进行开发的三段式大位移水平井。

2）不考虑温度及压力变化对钻井液密度等参数的影响。

3）不考虑套管内壁、井壁粗糙度以及管柱接头等对环空压耗的影响。

4）不考虑页岩地层水化等因素对地层破裂压力的影响。

笔者采用基于窄槽流动模型得到的用于同心环空压耗计算的达西公式[24]：

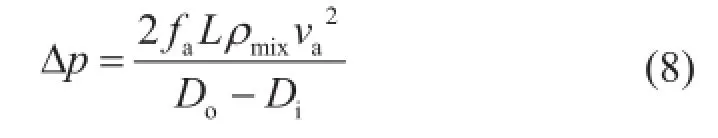
式中Δp表示环空压耗，MPa；fa表示环空摩阻系数，无因次；L表示井段长度，m；Do表示环空外径，mm；Di表示环空内径，mm；va表示钻井液环空平均流速，m/s。

由于重力的作用，管柱将会在井斜角较大的井段出现偏离井眼中心的情况，进而对环空压耗造成一定的影响。因此笔者将斜井段分为小斜度井段以及大斜度井段，其井眼测深分别为Lds和Ldl，并在大斜度井段以及水平段的压耗或压耗梯度计算中引入偏心系数（R）的影响。

垂直段、小斜度井段的环空压耗可以分别用式（9）、式（10）表示：

式中Δpds表示小斜度井段环空压耗，MPa； Lds表示小斜度井段测深，m。

大斜度井段环空压耗的计算公式为[25-26]：

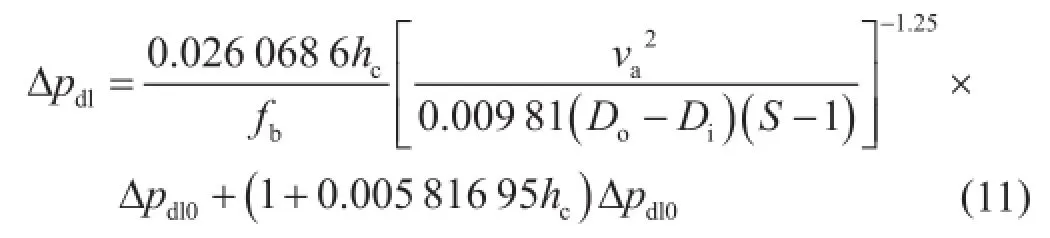
式中Δpdl表示大斜度井段环空压耗，MPa；hc表示无因次岩屑床厚度，计算方法详见本文参考文献[27]；S表示岩屑密度与钻井液密度之比，无因次；fb表示达西—维斯巴赫系数，无因次；Δpdl0表示大斜度井段无岩屑床时的环空压耗，MPa，可以表示如下：

式中Ldl表示大斜度井段测深，m；R表示偏心系数，无因次。

水平段的环空压耗梯度(Δp/ΔL)h可以表示如下：

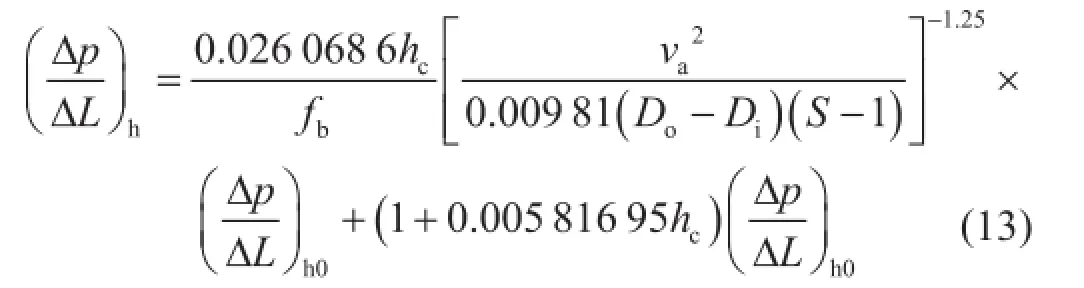
不考虑岩屑床时的水平段环空压耗梯度(Δp/ ΔL)h0为[28]：

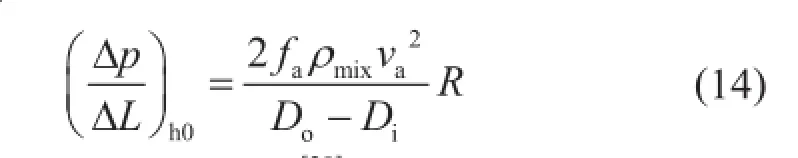
式中fa可以由式（15）确定[29]：

式中Re表示广义雷诺数，无因次；a，b表示摩阻系数常数，无因次；当环空钻井液处于层流状态时，a=24，b=21；而当环空钻井液处于紊流状态时，可以使用式（16）进行计算：

式中n为流性指数，无因次。

2.2 广义雷诺数

工程上常采用广义雷诺数（Re）来区分层流和紊流，Re＜2 100时为层流，Re≥2 100为紊流。不同流变模式的钻井液其广义雷诺数（Re）也不同，本文主要采用赫巴流体来进行分析计算，并需要与之前基于幂律流体建立的模型进行对比，它们的广义雷诺数可以表示如下[24]：

1)幂律流体的广义雷诺数（Repl）为：

式中K表示稠度系数，Pa·sn。

2)赫巴流体的广义雷诺数（Reahb）表示：

式中τ0表示屈服值，Pa。

2.3 偏心系数

实际钻井过程中，钻柱会在重力的作用下偏离井眼中心，这会对环空压耗产生一定的影响，这一影响可以通过引入偏心系数来进行修正。按照流动状态的不同可以分为层流偏心系数（Rlam）和紊流偏心系数（Rturb），分别用以下公式表示[28,30-32]：

式中e表示偏心距，mm；ε表示无因次偏心距，它还包含两种极端情况，同心环空ε＝0，完全偏心环空ε＝1。

3 实例分析

涪陵地区页岩气的开发对大位移水平井有着迫切的需求，本文针对该地区1口大位移水平井进行分析研究，主要考察赫巴流体的基本流变参数（流性指数、稠度系数、屈服值）和主要钻进参数（机械钻速、钻井液密度、钻杆转速）的变化对大位移水平井水平段延伸极限的影响，并将计算结果与采用幂律流体进行计算的结果进行比较分析。具体的计算参数如表1～3[24,33]所示，井眼轨道示意图如图1所示。

表1 井眼轨道设计参数表

表2 井身结构设计参数表

表3 输入模型的数据表

图1 井眼轨道设计图

通过计算可知，采用幂律流体钻井液得到的水平段延伸极限为2 564.2 m，而采用赫巴流体得到的水平段延伸极限为1 744.6 m。为了分析模型中的主要参数对水平段延伸极限的影响，笔者分别对赫巴流体的基本流变参数和水平段的主要钻进参数进行了敏感性分析。

3.1 基本流变参数

3.1.1 流性指数

1.企业员工。受访企业员工中男性占比为48.1%，女性占比为51.9%；年龄介于19-30岁占比为60%，年龄介于31-40岁占比为30%，超过40岁的占比为10%；月工资收入低于5000元的约占80%，月工资超过5000元的约占20%；专科学历、本科学历的占比均为43.6%，高中及以下、研究生学历占比均为7.4%。经走访相关部门确认，调查样本所体现的性别、年龄、收入、学历情况与企业实际基本相符，样本的代表性充足以确保研究的可信度。

从图2可以看出，流性指数对水平段延伸极限的影响显著，随着流性指数的增加，采用幂律流体和赫巴流体钻井液钻进的水平段延伸极限都逐渐减小，且采用幂律流体的水平段延伸极限要大于采用赫巴流体的水平段延伸极限，但是这种差距随着流性指数的增加在不断缩小。由于相对于幂律模式来说，赫巴流体能够更好地模拟实际钻井液的流变特性。因此如果在流性指数较小时采用幂律模式流体进行分析计算则可能会产生较大的误差，而采用赫巴流体则可以获得更加准确可靠的结果。

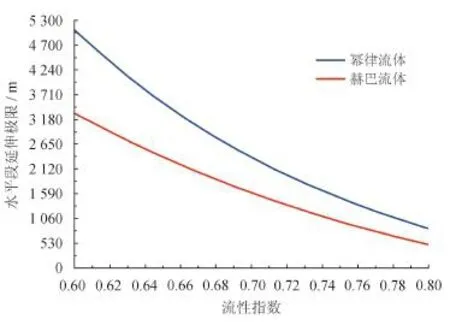
图2 流性指数对水平段延伸极限的影响图

3.1.2 稠度系数

从图3可以看出，从整体上来说，随着稠度系数的增加，水平段延伸极限逐渐减小，并且在同一稠度系数下，采用幂律模式钻井液得到的水平段延伸极限要大于采用赫巴模式所获的水平段延伸极限。

图3 稠度系数对水平段延伸极限的影响图

3.1.3 屈服值

赫巴模式与幂律模式的主要不同之处就在于赫巴模式考虑了屈服值这一参数，使得赫巴模式更加符合实际钻井液的流变特性。因此我们需要着重对屈服值进行分析研究。从图4可以看出，由于幂律模式中不存在屈服值这一参数，所以随着屈服值的增加，采用幂律模式钻井液的水平段延伸极限值保持不变，而采用赫巴模式流体的水平段延伸极限则随着屈服值的增加而逐渐较小。只有当屈服值为0 Pa时，赫巴模式与幂律模式没有任何区别，此时的水平段延伸极限一致。

图4 屈服值对水平段延伸极限的影响图

综上所述，从钻井液流变参数的角度来分析，如果采用幂律模式流体来建立大位移水平井裸眼延伸极限的预测模型可能会产生较大的误差；而采用赫巴模式流体进行建模则会更加符合实际。并且由上述分析可知，在采用赫巴模式钻井液进行钻进时，要获得更大的水平段延伸极限，应该在满足钻井液性能需要的情况下尽可能地降低流性指数、稠度系数以及屈服值。

3.2.1 机械钻速

由图5可知：随着机械钻速的增加，水平段延伸极限逐渐减小。这是因为随着机械钻速的增加，环空中的岩屑含量逐渐增加，造成环空压耗增大。并且在同一机械钻速下，采用幂律流体的水平段延伸极限要大于采用赫巴流体的水平段延伸极限。

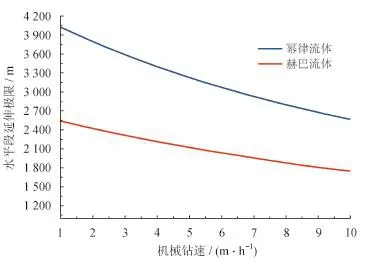
图5 机械钻速对水平段延伸极限的影响图

3.2.2 钻井液密度

图6 钻井液密度对水平段延伸极限的影响图

从图6可以看出，随着钻井液密度的增加，水平段延伸极限具有先增加后减小的趋势。并且在同一钻井液密度下，采用幂律流体的水平段延伸极限要大于采用赫巴流体的。因此，若采用幂律流体进行建模分析，可能会产生较大的误差并因此带来一些井壁稳定方面的安全事故隐患。

3.2.3 钻杆转速

从图7可以看出，钻杆转速对水平段延伸极限的影响也较为明显，总体上呈现一个随钻杆转速增加而增加的趋势。在同一钻杆转速下，采用幂律流体的水平段延伸极限要大于采用赫巴流体的水平段延伸极限，并且这种差距随着钻杆转速的增加而逐渐增大。

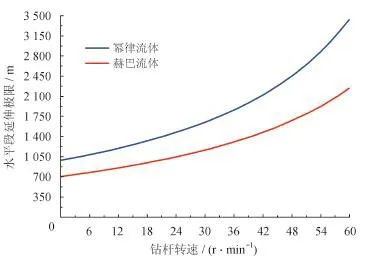
图7 钻杆转速对水平段延伸极限的影响图

综上所述,从钻进参数的角度来说，要获得较大的水平段延伸极限及裸眼延伸极限，应该在满足钻井需要的前提下尽量减小机械钻速，并增加转速，这都有利于环空岩屑的清除从而降低钻井液循环压耗，同时还要优化钻井液密度的取值。同时，采用赫巴

模式来进行计算分析会减少因之前采用幂律模式计算时所带来的误差和可能引起的钻井安全事故。

4 结论

考虑到赫巴流体相比于幂律流体能更加准确的描述实际钻井液的流变特性，笔者建立的基于赫巴流体的大位移水平井裸眼延伸极限预测模型，解决了大位移水平井在页岩储层中究竟可以打多远的问题，并且更加精确地预测了大位移水平井的裸眼延伸极限。

计算结果表明：由于考虑了屈服值的影响，采用赫巴流体计算的水平段延伸极限要小于采用幂律流体建模时的计算值。因此，采用赫巴流体进行建模可以减小因采用幂律流体建模分析时产生的误差，并降低因参数设计不合理而引起的钻井安全事故的可能性。对于大位移水平井的水平段延伸极限而言，在赫巴流体的三个基本流变参数（流性指数、稠度系数、屈服值）和三个主要钻进参数（机械钻速、钻井液密度、钻杆转速）中，水平段延伸极限会随着三个基本流变参数和机械钻速的增加而减小，而该极限会随着钻井液密度的增加先增加后减小，它也会随着钻杆转速的增加而增加。优化各个参数的取值有助于获得更大的水平段延伸极限，这对于页岩气的高效开发利用具有重要的作用。

[1] 梁睿, 童莉, 向启贵, 庄思源, 周学双. 中国页岩气开发的环评管理及建议[J]. 天然气工业, 2014, 34(6): 135-140.

Liang Rui, Tong Li, Xiang Qigui, Zhuang Siyuan, Zhou Xueshuang. Management of and proposals on environmental impact assessment (EIA) for shale gas development in China[J]. Natural Gas Industry, 2014, 34(6): 135-140.

[2] 杨华, 李士祥, 刘显阳. 鄂尔多斯盆地致密油、页岩油特征及资源潜力[J]. 石油学报, 2013, 34(1): 1-11.

Yang Hua, Li Shixiang, Liu Xianyang. Characteristics and resource prospects of tight oil and shale oil in Ordos Basin[J]. Acta Petrolei Sinica, 2013, 34(1): 1-11.

[3] 郭为, 熊伟, 高树生, 胡志明, 刘洪林, 于荣泽. 温度对页岩等温吸附/解吸特征影响[J]. 石油勘探与开发, 2013, 40(4): 481-485.

Guo Wei, Xiong Wei, Gao Shusheng, Hu Zhiming, Liu Honglin, Yu Rongze. Impact of temperature on the isothermal adsorption/ desorption characteristics of shale gas[J]. Petroleum Exploration and Development, 2013, 40(4): 481-485.

[4] 杜金虎, 杨华, 徐春春, 梁世军, 皮学军, 王红岩. 关于中国页岩气勘探开发工作的思考[J]. 天然气工业, 2011, 31(5): 6-8.

Du Jinhu, Yang Hua, Xu Chunchun, Liang Shijun, Pi Xuejun, Wang Hongyan. A discussion on shale gas exploration and development in China[J]. Natural Gas Industry, 2011, 31(5): 6-8.

[5]王伟吉, 邱正松, 钟汉毅, 黄维安, 赵欣, 董兵强, 等. 页岩储层温敏型P(NIPAm-co-AA)/nano-SiO2复合封堵剂的制备及特性[J]. 石油学报, 2015, 36(3): 378-384.

Wang Weiji, Qiu Zhengsong, Zhong Hanyi, Huang Wei'an, Zhao Xin, Dong Bingqiang, et al. Preparation and properties of thermosensitive poly(NIPAm-co-AA)/nano-SiO2composite blocking agent for shale gas reservoir[J]. Acta Petrolei Sinica, 2015, 36(3): 378-384.

[6]王道富, 高世葵, 董大忠, 黄旭楠, 王玉满, 黄金亮, 等. 中国页岩气资源勘探开发挑战初论[J]. 天然气工业, 2013, 33(1): 8-17.

Wang Daofu, Gao Shikui, Dong Dazhong, Huang Xunan, Wang Yuman, Huang Jinliang, et al. A primary discussion on challenges for exploration and development of shale gas resources in China[J]. Natural Gas Industry, 2013, 33(1): 8-17.

[7] 吴雪平. 漏失水平井固井技术在JY33HF井的应用[J]. 长江大学学报: 自科版, 2015, 12(17): 54-57.

Wu Xueping. Application of well cementing technology in JY-33HF well[J]. Journal of Yangtze University: Natural Science Edition, 2015, 12(17): 54-57.

[8] 梁玉平, 王建波. 涪陵区块12-4X页岩气水平井钻井关键技术[J].石油机械, 2014, 42(8): 57-61.

Liang Yuping, Wang Jianbo. Key drilling technologies for horizontal shale gas well 12-4X in Fuling block[J]. China Petroleum Machinery, 2014, 42(8): 57-61.

[9] 梁文利. 柴油基钻井液在涪陵礁石坝区块页岩气储层的应用[J]. 天然气勘探与开发, 2014, 37(3): 64-69. Liang Wenli. Application of diesel-based drilling fluid to shale-gas reservoirs in Jiaoshiba block, Fuling[J]. Natural Gas Exploration and Development, 2014, 37(3): 64-69.

[10] 石林, 汪海阁, 纪国栋. 中石油钻井工程技术现状、挑战及发展趋势[J]. 天然气工业, 2013, 33(10): 1-10.

Shi Lin, Wang Haige, Ji Guodong. Current situation, challenges and developing trend of CNPC's oil & gas drilling[J]. Natural Gas Industry, 2013, 33(10): 1-10.

[11] 王兰生, 廖仕孟, 陈更生, 郭贵安, 吕宗刚, 付永强. 中国页岩气勘探开发面临的问题与对策[J]. 天然气工业, 2011, 31(12): 119-122.

Wang Lansheng, Liao Shimeng, Chen Gengsheng, Guo Gui'an, Lü Zonggang, Fu Yongqiang. Problems and countermeasures of shale gas exploration and development in China[J]. Natural Gas Industry, 2011, 31(12): 119-122.

[12] 王红岩, 刘玉章, 董大忠, 赵群, 杜东. 中国南方海相页岩气高效开发的科学问题[J]. 石油勘探与开发, 2013, 40(5): 574-579.

Wang Hongyan, Liu Yuzhang, Dong Dazhong, Zhao Qun, Du Dong. Scientific issues on effective development of marine shale gas in southern China[J]. Petroleum Exploration and Development, 2013, 40(5): 574-579.

[13] Sonowal K, Bennetzen B, Wong KM, Isevcan E. How contin-

uous improvement lead to the longest horizontal well in the world[C]//SPE/IADC Drilling Conference and Exhibition, 17-19 March 2009, Amsterdam, The Netherlands. DOI: http: //dx.doi. org/10.2118/119506-MS.

[14] Gupta VP, Yeap AHP, Fischer KM, Mathis RS, Egan MJ. Expanding the extended reach envelope at Chayvo Field, Sakhalin Island[C]//IADC/SPE Drilling Conference and Exhibition, 4-6 March 2014, Fort Worth, Texas, USA. DOI: http://dx.doi. org/10.2118/168055-MS.

[15] 覃成锦, 高德利, 唐海雄, 魏宏安. 南海流花超大位移井井身结构设计方法[J]. 石油钻采工艺, 2006, 28(1): 13-14.

Qin Chengjin, Gao Deli, Tang Haixiong, Wei Hong'an. Casing program design method for Liuhua mega-extended-reach wells in South China Sea[J]. Oil Drilling & Production Technology, 2006, 28(1): 13-14.

[16] Gao Deli, Tan Chengjin, Tang Haixiong. Limit analysis of extended reach drilling in South China Sea[J]. Petroleum Science, 2009, 6(2): 166-171.

[17] 孙腾飞, 高德利. 水平井钻井轨迹设计与控制一体化方法[D].北京: 中国石油大学(北京), 2013.

Sun Tengfei, Gao Deli. Research on well trajectory design & control in horizontal drilling[D]. Beijing: China University of Petroleum (Beijing), 2013.

[18] 罗伟, 付建红, 宋科熊, 许超. 大位移井水平井极限延伸长度预测研究[J]. 科学技术与工程, 2013, 13(35): 10623-10627.

Luo Wei, Fu Jianhong, Song Kexiong, Xu Chao. Prediction of limit extension length of horizontal extended-reach well[J]. Science Technology and Engineering, 2013, 13(35): 10623-10627.

[19] 吴朗. 小井眼窄间隙注水泥设计与软件系统研制[D]. 成都:西南石油大学, 2012.

Wu Lang. Design and software development of narrow gap system cementing in slim hole drilling[D]. Chengdu: Southwest Petroleum University, 2012.

[20] 步玉环, 王瑞和, 程荣超. 油气固井纤维水泥浆性能研究[J].石油钻采工艺, 2005, 27(2): 25-27.

Bu Yuhuan, Wang Ruihe, Cheng Rongchao. Performance of fiber cement slurry for well cementation[J]. Oil Drilling & Production Technology, 2005, 27(2): 25-27.

[21] 王乐顶. 页岩气水平井固井前置液体系研究及应用[D]. 成都:西南石油大学, 2014.

Wang Leding. Research and application of shale gas horizontal well cementing pre-fluid system[D]. Chengdu: Southwest Petroleum University, 2014.

[22] 王斌斌, 王瑞和, 步玉环. 不同流态下水泥浆环空顶替的数值模拟研究[J]. 钻井液与完井液, 2010, 27(3): 76-78.

Wang Binbin, Wang Ruihe, Bu Yuhuan. Numerical simulation on cementing displacement in different flow patterns[J]. Drilling Fluid & Completion Fluid, 2010, 27(3): 76-78.

[23] Martins AL, Aragäo AFL, Calderon A, Leal RAF, Magalhäes JVM. Silva RA. Hydraulic limits for drilling and completing long horizontal deepwater wells[C]//SPE International Thermal Operations and Heavy Oil Symposium and Western Regional Meeting, 16-18 March 2004, Bakersfield, California, USA. DOI:http:// dx.doi.org/10.2118/86923-MS.

[24] 樊洪海. 实用钻井流体力学[M]. 北京: 石油工业出版社, 2013.

Fan Honghai. Fluid mechanics of practical drilling[M]. Beijing: Petroleum Industry Press, 2013.

[25] 汪海阁, 刘希圣. 水平井段环空压耗研究[J]. 西部探矿工程, 1995, 7(6): 25-28.

Wang Haige, Liu Xisheng. Analysis of annular pressure losses in horizontal section[J]. West-China Exploration Engineering, 1995, 7(6): 25-28.

[26] 李洪乾, 杲传良. 大斜度井环空压耗模式的应用及分析[J]. 钻采工艺, 1996, 19(1): 13-14.

Li Hongqian, Gao Chuanliang. Application and analysis of annular pressure losses pattern in high angle wells[J]. Drilling & Production Technology, 1996, 19(1): 13-14.

[27] 汪海阁, 刘希圣, 丁岗. 水平井段岩屑床厚度模式的建立[J].中国石油大学学报: 自然科学版, 1993, 17(3): 25-32.

Wang Haige, Liu Xisheng, Ding Gang. The model of cuttings bed thickness in horizontal well section[J]. Journal of China University of Petroleum: Edition of Natural Sciences, 1993, 17(3): 25-32.

[28] Kelessidis VC, Dalamarinis P, Maglione R. Experimental study and predictions of pressure losses of fluids modeled as Herschel-Bulkley in concentric and eccentric annuli in laminar, transitional and turbulent flows[J]. Journal of Petroleum Science and Engineering, 2011, 77(3/4): 305-312.

[29] Millheim KK, Tulga SS. Simulation of the wellbore hydraulics while drilling, including the effects of fluid influxes and losses and pipe washouts[C]//SPE Annual Technical Conference and Exhibition, 26-29 September 1982, New Orleans, Louisiana, USA. DOI: http: //dx.doi.org/10.2118/11057-MS.

[30] Bailey WJ, Peden JM. A generalized and consistent pressure drop and flow regime transition model for drilling hydraulics[J]. SPE Drilling & Completion, 2000, 15(1): 44-56.

[31] Erge O, Ozbayoglu EM, Miska SZ, Yu Mengjiao, Takach N, Saasen A, et al. The effects of drillstring-eccentricity, -rotation, and -buckling configurations on annular frictional pressure losses while circulating Yield-Power-Law fluids[J]. SPE Drilling & Completion, 2015, 30(3): 257-271.

[32] Haciislamoglu M. Practical pressure loss predictions in realistic annular geometries[C]//SPE Annual Technical Conference and Exhibition, 25-28 September 1994, New Orleans, Louisiana, USA. DOI:http://dx.doi.org/10.2118/28304-MS.

[33] 马庆涛, 葛鹏飞, 王晓宇, 贾江鸿. 涪页HF-1页岩气水平井钻井关键技术[J]. 石油机械, 2013, 41(8): 107-110.

Ma Qingtao, Ge Pengfei, Wang Xiaoyu, Jia Jianghong. Key technology of shale gas horizontal drilling in well HF-1 of Fuye[J]. China Petroleum Machinery, 2013, 41(8): 107-110.

(修改回稿日期 2016-07-04 编 辑 凌 忠）

Analysis on the open-hole extension limit of a shale-gas extended-reach horizontal well based on Hershel–Bulkley fluids

Li Xin1, Gao Deli1, Diao Binbin1, Zhou Yingcao2
(1. Key Laboratory of Petroleum Engineering Education Ministry, China University of Petroleum, Beijing 102249, China; 2. CNPC Drilling Research Institute, Beijing 102249, China)
NATUR. GAS IND. VOLUME 36, ISSUE 10, pp.85-92, 10/25/2016. (ISSN 1000-0976; In Chinese)

The open-hole extension limit of an extended-reach horizontal well is mainly controlled by annulus pressure loss and formation breakdown pressure, and the description of annulus pressure loss is greatly affected by the rheological pattern of drilling fluids. The actual rheological behavior of drilling fluids can be better simulated in the Hershel–Bulkley model. In this paper, a model for the open-hole extension limit of an extended-reach horizontal well in shale gas reservoirs was developed based on the Hershel–Bulkley fluids. Then, the effect of basic rheological parameters (e.g. liquidity index, consistency coefficient and yield value) and main drilling parameters (e.g. rate of penetration, drilling fluid density and drill pipe rotation) of Hershel–Bulkley fluids on the extension limit of horizontal section of an extended-reach horizontal well were investigated through case studies, and compared with the calculation results of the power-law fluid model. It is shown that, in the same condition, the result based on Hershel–Bulkley fluids is lower than that of the power-law fluid, indicating that the new prediction model is more reliable. Parameter sensitivity analysis shows that the extension limit of horizontal section decreases with the increase of three basic rheological parameters and the penetration rate, but increases with the increase of drill pipe rotation. Besides, it increases and then decreases with the increase of drilling fluid density. It is concluded that this optimization method for rheological and drilling parameters of Hershel–Bulkley fluids is conducive to solving the running distance of extended-reach horizontal wells in shale gas reservoirs and predicting its open-hole extension limit.

Shale gas; Extended-reach horizontal well drilling; Hershel–Bulkley fluids; Open-hole extension limit; Rheological parameter; Drilling parameter; Optimization method

10.3787/j.issn.1000-0976.2016.10.011

国家自然科学基金创新研究群体项目“复杂油气井钻井与完井基础研究”（批准号：51521063）、国家重点研发计划课题“钻井工艺及井筒工作液关键技术研究”（编号：2016YFC0303303）。

李鑫，1990年生，博士研究生；主要从事油气井力学与控制工程方面的研究工作。地址：（102249）北京市昌平区府学路18号。电话：（010）89733702。ORCID: 0000-0003-0238-352X。E-mail: lixin0102@126.com

高德利，1958年生，中国科学院院士，教授，博士生导师，博士。地址：（102249）北京市昌平区府学路18号。E-mail: gaodeli@cast.org.cn