图像的分形几何维数和系数模拟
图像的分形几何维数和系数模拟
几何学是研究物体组成结构及形态关系的一门学科。欧几里德几何学的基本构图元素是点、线、面,几何物体由点、线、面的组合而成,几何物体元素间的数量关系可通过解析几何进行公式化表述。但如果我们仔细审视我们生活的这个星球,甚至将目光放得再远一些直至整个宇宙,我们不难发现欧几里德几何学表述能力存在许多不足,对于在自然界中广泛存在的山脉、河流、宇宙星系等客观物体,由于它们的具有复杂的内部结构,欧几里德几何学在描述这些不规则形状物体及其内部细节方面存在很多不足。另外,随着几何学研究的不断发展,人们研究了康托集合、柯可曲线、斯尔宾斯基三角形等几何形状,发现欧几里得几何遇到了前所未有的挑战,欧几里得几何因无法准确描述这些几何结构而只能给它们标上“病态”标签从而排除在研究范围之外。1975,Mandebrot质疑欧几里得几何学的维数概念,他针对英国的海岸线问题进行了深入研究,他发现:测量得到的海岸线长度依赖尺子的尺度,欧几里德几何的长度概念在处理海岸线问题时遇到了困难,为了克服理论上的困难, Mandebrot提出用自相似维数概念,并用“Fractal”(分形)一词来描述海岸线等不规则几何形状,经过不断的深入研究,分形几何理论逐渐形成了独立的学科体系,体系内容不断得到丰富和完善,。
分形实例
康托集合
设实数区间[0,1] 为E0,令同样方法去掉E1两个子集中间三的三分之一部分,如此循环往复,逐步得到Ek,Ek是由2k个长度各为3k的区间组成,令F=则称F为三分Cantor集。如图1所示。

图1 康托集合
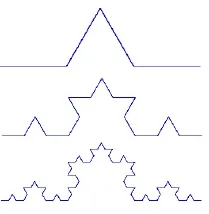
图2 柯克曲线
柯克曲线
设E0是长度为1的线段,按照和三分康托集一样的方法去掉中间三分之一,在空白处用等边三角形的另两边补充得到E1,按照同样的规则对E1进行操作,设k为操作次数,当
k→∞时得到的极限曲线F,F称为柯克曲线,如图2所示。
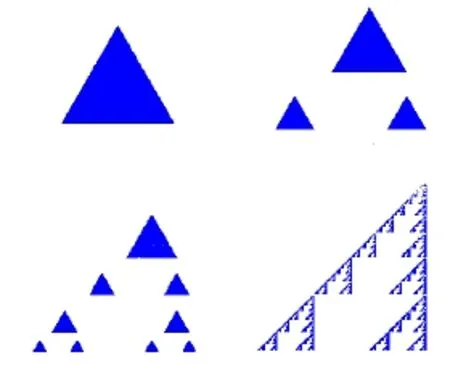
图3 斯尔宾斯基三角形
斯尔宾斯基三角形
任意三角形,取三边的中点,并将中点连接起来,将中点围成的三角形挖掉,得到三个的三角形,采用同样的方式挖掉三个三角形的中心部分,得到九个三角形,以此类推下去,就会得到如图3所示的图形,该图形成为斯尔宾斯基三角形。
从传统欧几里德几何角度分析,康托集合和柯克曲线的长度为零,斯尔宾斯基三角形的面积也为零,这些图形显然与欧几里德几何的结论矛盾,因为一维物体长度不可能为零,二维结构的面积也不肯能为零,因此按照欧几里德几何的逻辑上述图形都是“病态”的。仔细分析康托集合、柯克曲线、斯尔宾斯基三角形不难发现,它们的共同特征是具有精细结构,即由任意小的细节构成;整体与局部具有自相似性。
自相似性和自相似维数
如果物体的整体缩小后能够与局部重合,我们称这样的物体为分形物体,物体的这种特征称之为自相似,定义自相似维数为:
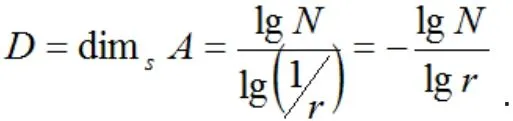
上式中D称为自相似维数,N为物体的细节个数,r为相似比。利用上式进行计算,得到康托集合的自相似维数是,柯克曲线的自相似维数是,斯尔宾斯基三角形的自相似维数是,很明显,物体的自相似维数一定是整数。
康托集合、柯克曲线和斯尔宾斯基三角形在欧几里德几何理论框架内都属于病态图形,但在分形几何理论体系内,它们具备了丰富的数学内涵,即具有严格的自相似特征,并且它们的自相似维数都是小数。另外需要指出的是自相似维数和传统的欧几里德几何维数是相容的,即传统几何物体的自相似维数和欧几里德维数相等。因此自相似维数的引入丰富了传统维数概念的内涵。

图4 斯尔宾斯基三角形计算结果
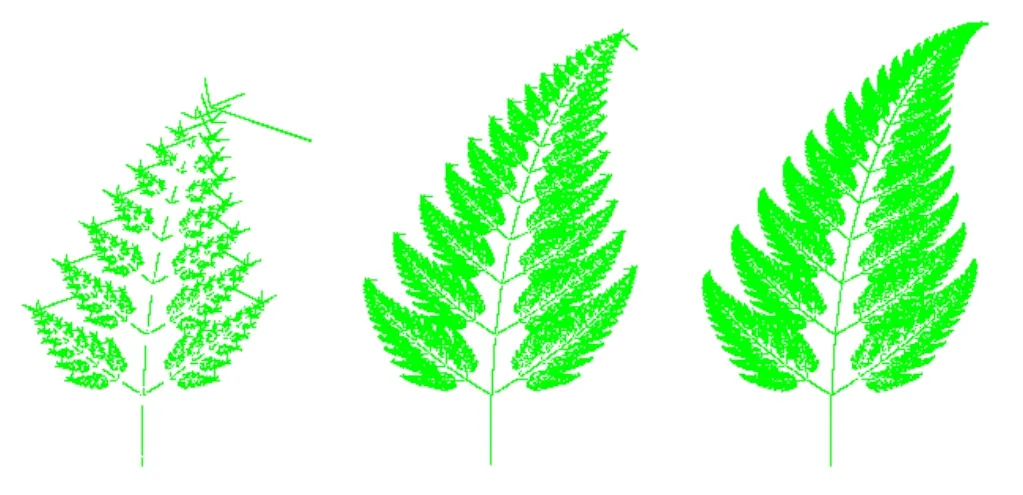
图5 橛子树模拟结果
分形图像的构造算法
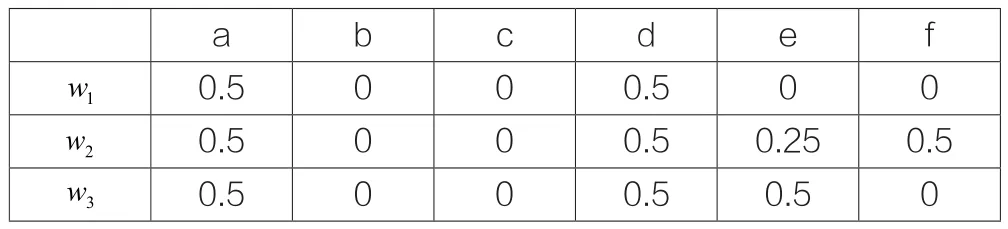
表1 斯尔宾斯基三角形的变换系数表
康托集合、柯可曲线也可通过相同的方法计算得到。不仅几何结构可以采用上述算法计算得到,自然物体同样也可以用相同的算法进行模拟,表2是橛子树的构造算法系数表,图5为计算模拟结果。
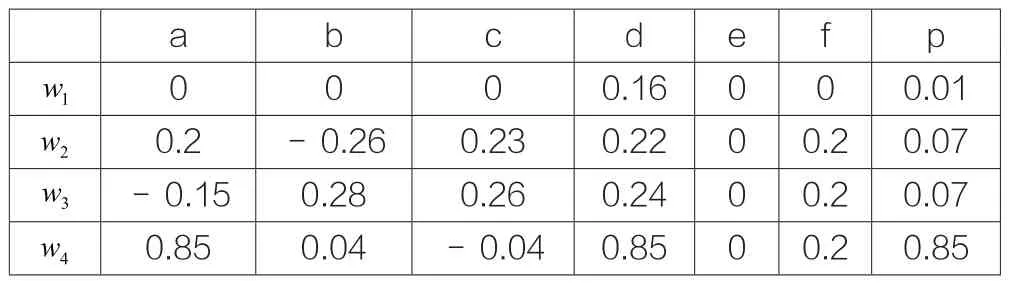
表2 橛子树的变换系数表
计算结果表明:具备自相似特征的分形物体可以采用几个仿射变换的方法进行构造,该构造的核心问题是选取合适的仿射变换系数。自然物体虽不具备严格的自相似特征,但它们普遍具有统计自相似性或局部自相似性,仍然可以通过仿射变换进行构造。因为变换系数的数据量远小于实际图像的数据量,从而可以实现数据压缩的目的。有些情况下我们需要实现图像目标的自动识别,而变换系数描述了图像细节,因此可以通过对比变换系数的方法实现计算机目标自动识别。
10.3969/j.issn.1001- 8972.2016.20.025

