从混凝土历史发展长河中学习理解A定则B公式之二（Ⅰ）

王永逵，王健，耿加会，余春荣，冯立艳

（1.上海奇齐科技开发公司，上海　201600；2.河南舞阳县惠达公路工程公司，河南　舞阳　462400；3.建筑材料工业技术情报研究所，北京　100024；4.四川德阳明鸿商品混凝土有限公司，四川　德阳　618099）

从混凝土历史发展长河中学习理解A定则B公式之二（Ⅰ）

王永逵1，王健1，耿加会2，余春荣3，冯立艳4

（1.上海奇齐科技开发公司，上海201600；2.河南舞阳县惠达公路工程公司，河南舞阳462400；3.建筑材料工业技术情报研究所，北京100024；4.四川德阳明鸿商品混凝土有限公司，四川德阳618099）

阿勃莱姆斯的A定则是在费雷特普适公式基础上的发展和提高，对混凝土强度理论具有里程碑的意义。保罗米的B公式是在A定则基础上的简化，使数理统计对混凝土中的应用进入新阶段。但与A定则没有质的区别，都是对混凝土强度期望值估计值的计算，其结果应该很接近。A定则-B公式成了现代混凝土的基础理论之一，有很强的现实指导意义。

A定则-B公式；期望值；预报；控制

1　B 公式是 A 定则的简化

A 定则的公式拟合与应用运用起来仍显得有点不方便。20余年后，在满足强度和水灰比估算值要求的前提下，1930年瑞典科学家的保罗米﹙Bolmy﹚通过大量试验和计算，把阿勃莱姆斯的双曲线部份线段﹙W/B＝0.4～0.8﹚，用一元回归的方法建立了“在标准条件下，对给定原材料，混凝土强度与灰水比（C/W）近似成正比” 关系的 B 公式。在 B 公式中，强度只与灰水比（C/W）近似成正比的关系，但并非否认混凝土强度与水泥、砂石质量等其它因素的因果关系，而是基于数学原理，在标准条件下，对给定原材料，大量试验数据表明因变量混凝土强度﹙Y﹚只能与可检测控制的自变量灰水比（C/W）建立近似的线性关系。而除灰水比（C/W）以外的其它影响因素都因其是随机变量，只能在因变量﹙yi﹚中得以反应。同时，B 公式的建立不是从天上掉下来的，而是在大量试验基础上的。散点图的趋势表明，混凝土强度﹙Y﹚与自变量﹙X﹚有明显的线性特征，它符合“认识来源于实践”的辩证唯物主义哲学原理。水泥、砂石质量等其它因素对强度影响，是通过大量试验数据我们称其为样本中的子样﹙xi，yi﹚数据来体现其不可缺失的影响。正是由于除水灰比以外其它众多因素的影响，才使因变量混凝土强度﹙Y﹚具有不确定性数据随机变量特性。如再将水泥和砂石等列入多元回归方程也是重复因子，无益于估计值准确性的提高。这里可以用“此处无声胜有声”来形容。这一数理统计的回归分析方法，不仅是依据最小二乘法的统计学原理，也是源于几千年的混凝土反复实践－认识－再实线－再认识，同时也亦经200余年来的工程应用所证实。“实践是检验真理的唯一标准”，B 公式的可信度不仅是过去，在现在或可见的未来也能经得起实践检验。

我国对保罗米的 B 公式介绍，可见于1981年中国建筑出版社出版的高校试用教材《混凝土学》[1]，表达如下：

式中：

K1，K2——经验系数。

C/W——灰水比。

R——规定龄期的混凝土抗压强度。

由于 R 是一个随机变量的统计值估算值，具有不确定性，对给定灰水比的28d 强度只是期望值的估计值标示为R28，以示与一般确定性的设计强度或配制强度的 R28区别。因此式（1）也可表示为：

在配合比设计中利用式（1），给定配制强度 R28，可计算出试配时所需要的水灰比估计值；也可已知 W/C估算，这对混凝土配合比设计和施工技术管理有重要的应用价值。

在《混凝土学》一书中并未介绍式（1）是谁发明的，上述瑞典料学家保罗米1930年发明了 B 公式，在我国可能是苏联专家上世纪50年代末来华讲学时介绍的。另在和唐明述等译英国科学家 F.M. 李著《水泥和混凝土化学》[4]和张绶庆译日本笠井芳夫著的《材料科学导论》[2]中，也有类似的式（1）表达式：S＝X+Y﹙C/W﹚，按他们的说法该线性公式是英格·利塞﹙Inge lyse﹚发明的，式中 X 和 Y 是回归系数，这种表达式除用不同的字符外，与式（1）式没有区别。看来“在标准条件下，对给定原材料，混凝土强度可与 C/W近似成正比”的关系不只是保罗米一人，在当时除瑞典、前苏联等北欧国家以外，国际混凝土界己有较为广泛的认知。严格的说，B 公式中 R 并非与 C/W 完全成比，它还有一常数项“K1”影响，只是近似而已。后来在 B 公式中引入混凝土强度等级（Rc）和水泥实测强度（fce）后，回归系数“K1、 K2”演变成“A、B”或“aa、ab”，只是两回归系数值的变化，强度与灰水比的近似关系并没有变化。这种把强度简化为与灰水比成正比的线形近似关系，是保罗米在阿勃莱姆斯基础上的进步。

在 B 公式拟合中，K1、K2两回归系数取决于样本中的“子样”﹙xi，yi﹚的具体数据。条件不同、时代不同，由公式拟合时的样本子样的﹙xi，yi﹚自然会有变化，B 公式的K1、K2也应有变化，W/B 的估算结果也不会一样，如表1介绍的美国 ACI211.1推荐的引气型与非引气型的 W/C 值就有明显的差别。因此，要求普通混凝土配合比设计的 W/B 估算适用于一切类型混凝土是不妥的。同时，随着混凝土科技的进步，“规程”每隔几年就需要修订。要遵循不同质的问题，用不同的方法解决，一把钥匙开一把锁。

表1　水灰比与混凝土抗压强度的相互关系

2　B 公式的拟合

上述讨论强调了 B 公式应用必须注意使用条件，生产中都希望找到更切合自已公司生产实际的 B 公式。那么，根据积累的样本数据﹙xi，yi﹚运用最小二乘法理论上的回归分析，求得 B 公式中 K1、K2两回归系数，建立 B 公式的过程，称之为 B 公式拟合。

2.1什么是回归分析？什么是最小二乘法？

在数理统计中，用最小二乘法，处理量与量之间非确定性关系问题的数学方法称之为回归分析。根据所研究的自变量个数的多少，分一元回归分析和多元回归分析两类，在每一类中又以自变量与考核标﹙因变量﹚之间呈线性和非线性关系，有线性回归分析和非线性回归分析两种。其中一元线性回归是回归分析中最常用，同时也是最基本的回归分析方法。

研究两个变量 X 和 Y 之关系的问题称为一元回归分析。这里 X 是自变量，它的值是事先给定的或可以控制、可精确观察的普通变量[3,4]，如混凝土配合比设计中根据已知配制强度要求的 W/B，或已知混凝土早期强度求R28等，都是自变量（X），而 W/B 混凝土强度 R28（Y）是因变量，是事件发生前不能准确预测的随机变量，是我们要考查的指标称之为期望值的估计值、平均值。如本例中的混凝土的灰水比（X）与强度（Y）之间建立的近似正比线性关系，研究它们之间关系建立相关公式的方法称之为一元线性回归分析。

现暂以笔者在从事商品混凝土技术工作中，积累的27组部份普通商品混凝土自变量水胶比（Xi）和因变量强度（Yi）数据（表2）用列表计算的方法拟合 B 公式，重在学习体验前人发明最小二乘法的计算过程的艰辛，进而体会现代电脑比人脑计算的便捷。

试以表2的 Xi和 Yi数据做的散点图1，初步判断 Xi和 Yi存在近似的直线性关系式（3），因变量 yi任意一点与直线的关系存在有误差 εi式（4）：

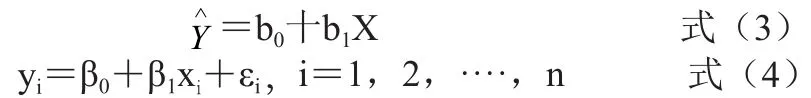
式（4）中：

β0和 βi——回归系数。

εi——第 i 次试验中的误差（i=1，2····，n）。

图1　散点图

假定 εi是一相互独立、且服从正态分布 N（0，σ2）的随机变量。问题是如何求得 b0、b1这两个回归系数的问题，有了它们就可建立回归方程式了了。根据式 （4）每个 xi都可以算出变量 yi对应的估计值 ，与观察值 yi之间的偏差 εi为：

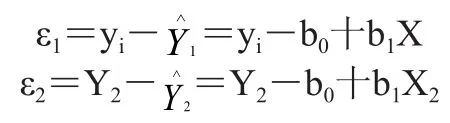
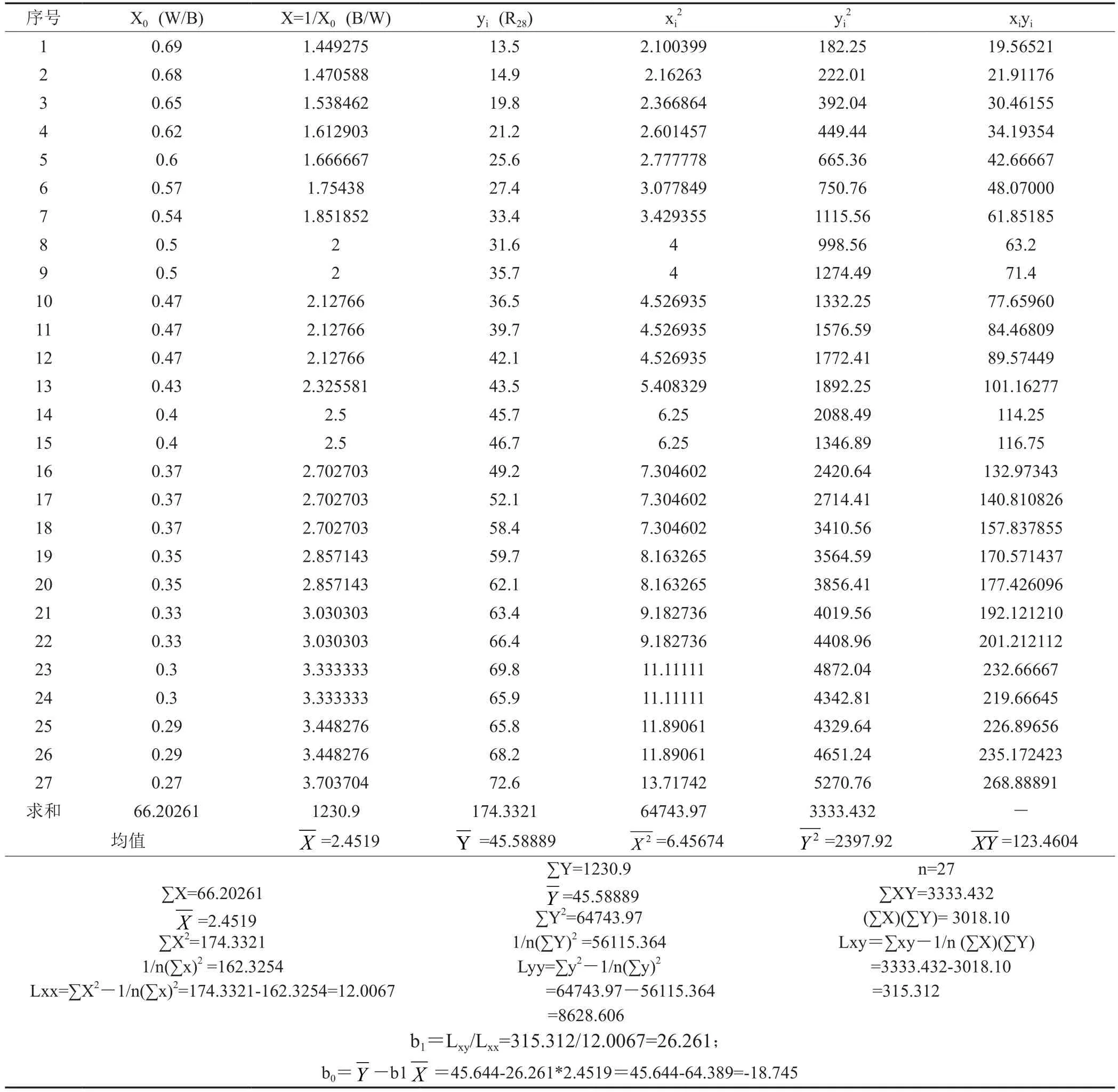
表2　列表计算　b0和b1数据表

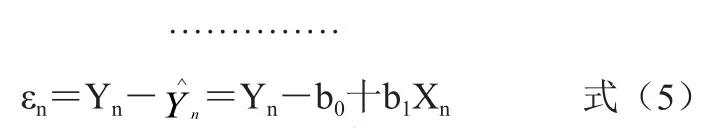
一个很自然的想法是，如果在 n 次试验中，y的观测值与估计值之间的偏差总和 ε1＋ε2＋·····＋εn愈小，则可认为回归直线与观测值拟合得愈好。又由于 εi中有正有负，如直接将它们的和作为衡量 y 和 x 之间的总偏差程度，就可能因 εi正负相消而使偏差总和为零作出错误的判断，这显然是不合理的。因此，通常用每个偏差平方和的方法，即

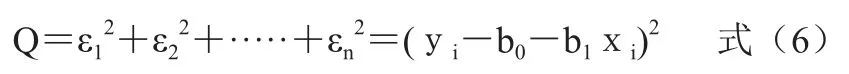
Q 值的大小取决于 b0和 b1，如果能找到一组 b0、b1值使Q 达到最小，这时的 b0、b1值为系数的必将是与观测值拟合得最好线性回归。求得这样一组 b0、b1值的方法可以用最小二乘法求得。所谓最小二乘法就是使得 Q 值达到最小的一种计算回归系数（b0，b1）值的方法[4]。

根据数学上求极值的原理，要使 Q 达到最小，应使 b0和b1偏导数为0。

将 Q 的表达式代入，可得

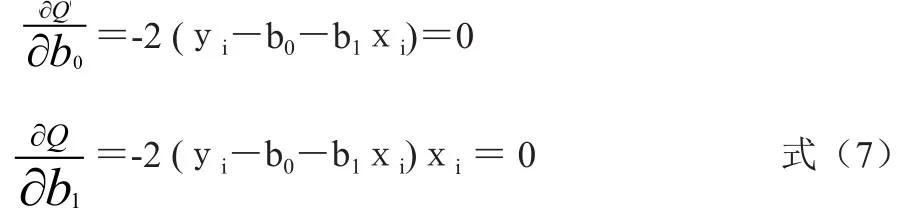
式（8）为一二元一次方程，其求解如下：

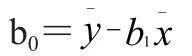
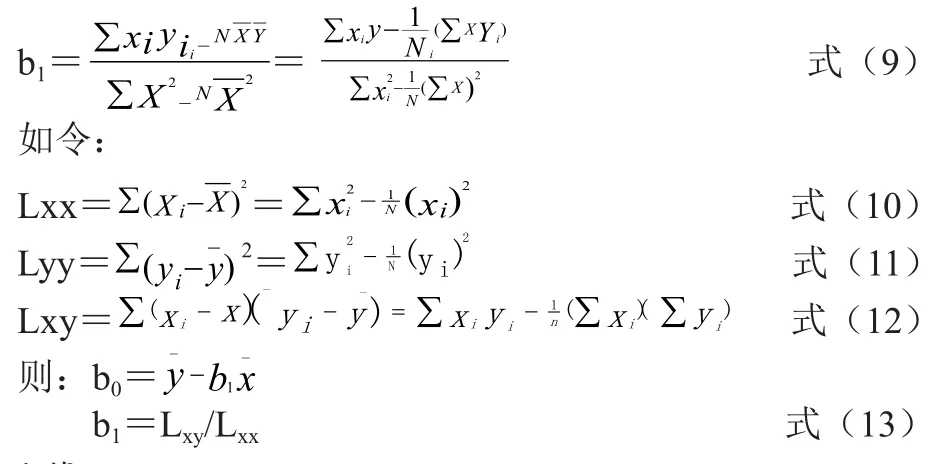
2.2计算 b0和 b1

根据式（13）列表计算 b0和 b1，详见表2。

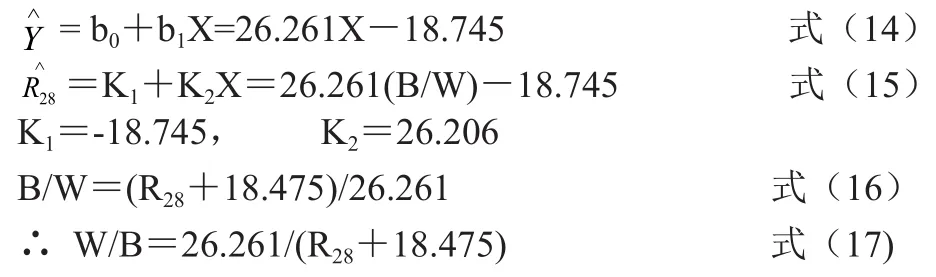
2.3一元线性回归方程的显著性检验

一元回归的显著性检验有三种方法，它们是：相关系数检验、方差分析检验和剩余标准差检验。三种相关性检验的方法都是从数学上说明用一元线性回归与实际强度与胶水比直线相关的程度。在这里只利用现有公式，对相关系数检验的方法来检验与实际线性相关的程度，不介绍另两种检验方法和公式推导。

2.4相关系数 r 值计算与判断步骤

2.4.1由变量 X 和 Y 的观察值计算 r 值

相关系数是衡量两个变量（X，Y）之间线性相关程度的一个量，用r表示。对 X、Y 两个变量进行 n 次观测，如第i 次的观测为（Xi，Yi）, 则它们之间的相关系数 r 用下式计算：

2.4.2临界值

给定检验水平a，在相关系数检验表中查自由度ν＝n－2时的临界值 r0（n 是对变量 x 和 y 的观察次数，即数据对子样的个数）；本例给定检

验水平 a＝0.01，n＝27，查“相关系数检验表”中査自由度 ν＝n－2＝25时的临界查得r0＝0.4869

2.4.3判断规则

当 |r|＞r0时，认为变量 x 和 y 之间的线性关系是显著的，建立的回归方程是合理的；当 |r|＜r0时，认为变量和y之间的线性关系是不显著的，建立的回归方程没有实际意义。

当 |r| 愈接近1.0，则相关性愈好，|r|＝0为完全相关，方程为一直线。

现查得r0＝0.4869。

∵ |r| ＝0.9800＞＞r0＝0.4869；

∴ 所拟合的——元回归线性方程相关性特别显著。

3　B 公式的预报与控制

3.1预报

预报与控制是在 B 公式的一元回归方程建立与显著性检验合格后才进行的。所谓“预报” 是指已知胶水比（X＝ X0）时，利用建立的 B 公式来预报与 X0对应的值在一个什么置信度范围出现以及在验收要求下，R28能否满足验收要求，达到“预防在先，事预则立”的目的。其依据，正如以开始就强调的，我们现在讨论的 和 R28都是属于不确定性数据的统计值，它有一定的分布规律。大量的实践证明，灰水比（X0）一定，强度的分布服从正态分布，于是得到以下三个置信度的预报区间：

公式预报示意图见图2。

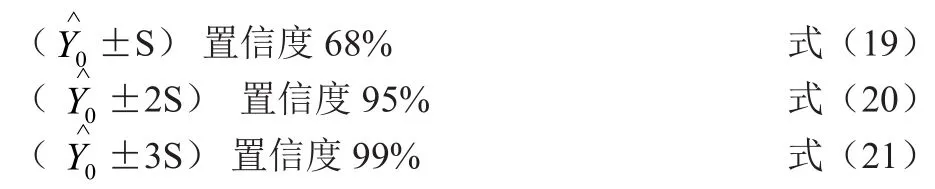
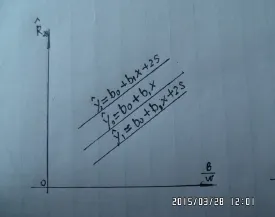
图2　公式预报示意图

3.2普通商品混凝土 C30的预报与控制实例

普通商品混凝土 C30的预报与控制实例，详见表3。根据问题的要求，选择式（19）～式（21）中的置信度区间作为预报 X＝X0时，对应观测值 Y0出规的机率区间。如图2。 一般要求置信度95% 时，b0＋b1X±2S 认为经济技术合理。即：则回归直线的两平行线。

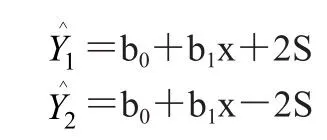
表3　普通商品混凝土 C30配合比实例

表4　混凝土强度标准差

以表3普通 C30商品混凝土为例：

已知：W/B＝0.46，X0＝B/W＝2.169，质量控制水平S＝3.5MPa

代入公式：

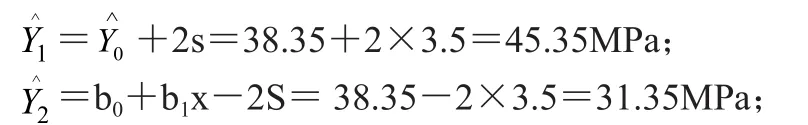
混凝土‘预测’置信度的有关规则对我们的启示是：强度是一个随机变量，在生产中由于受到许多难以控制因素的影响，强度值的波动不可避免。既使是在置信度68% 范围内，C30混凝土的在生产检验中强度的波动可能在34.7～41.7MPa 之间，高低之差在20% 以上。在置信度95% 范围内，波动也可能在31.4～45.4MPa 之间，可能出现的高低之差，将达到30% 以上。由此，我们在混凝土对比试验中根据取值的判断应慎重，不能仅跟据一组试验的取值结果，就判断其优劣。不同条件下的对比，更不能简单下结论。数据的取值应遵循一定的条件和一定的取值法则，否则可能得出错误的结论。关于数据的合理取值，需另在专项讨论中论述，这里只是提醒关注非确定性数据随机变量的特点。

3.3控制

（1）控制什么？控制的许可范围有多大？

所谓控制，就是在生产过程中对给定的原材料，对混凝土强度影响最大的水胶（灰）比在置信度95% 即范围内，应控制在什么范围？才能满足抗压强度合格95% 的要求。工程实践告诉我们对混凝土的质量控制，对给定原材料，影响最大的是水胶（灰）比，在生产过程中必须时刻关注砂石含水量的变化，即时采取应对措施并严格禁止现场应加水，始终将水胶比控制在一个许可范围，做到预防在先确保混凝土质量。如3.2章节实例 C30混凝土，原设定的水胶比期望值 W/B＝0.46

计算结果表明：在95% 的置信度内，以 W/B＝0.46为中心，水胶比应控制在0.41～0.52范围内。既不能大于0.52，也不必低于0.41。此一要求正好与“规程”中除按配制强度计算得到的 W/B 估算值进行试配外，还须另外（W/ B±0.05）做三个配合比试配是一致的。如 C30的 W/B 估算值，W/B＝0.46，它的 ±0.05，与要求质量控制的 W/B 在（0.41～0.52≈0.46±0.05＝0.41～0.51）基本一致。合格的混凝土抗压强度可有95% 的大概率将出在这个范围。水胶比必须＜0.52，否则混凝土抗压强度有可能低于30MPa，出现不合格。

（2）实际生产中水胶比不变是相对的，变是绝对的。我们目标只能是控制在一个许可范围内。

（未完待续）

[1] 重庆建筑工程学院，南京工学院合编．混凝土学[M]．北京：中国建筑工业出版社，1981,7

[2] [美]戴维·达尔文﹙Darid Darwid﹚著．混凝土[M]．吴科如，张雄，姚武，等译，北京：化学工业出版社，2005,1.

[3] [日]笠井芳夫著材料科学导论[M]．张绶庆译，北京：中国建筑出版社，1981,2.

[4] 浙江大学盛骤，谢式千，潘承毅著．概率论与数理统计(第二版) [M]．北京：高等教育出版社1989,8．

[5] 王永逵，陆吉祥，著．材料试验与质量管理的数学方法[M]．北京：中国铁道出版社，1990．

[6] [英]F·M·李著．水泥和混凝土化学(第三版)[M]．唐明述等译．北京：中国建工出版社，1980．

[7] 王元．减水剂的应用对使用水灰比定则的影响[J]．商品混凝土，2013(3)：1-6．

［通讯地址］上海松江区荣乐中路228弄北九峰小区152号302室（201600）

王永逵（1934—），前兰州铁道学院土木系建材室主任。