标准BP神经网络算法和附加动量法在沉降监测中的应用研究
李波,柳华桥,戴鑫,贾志强
(天津市测绘院,天津 300381)
标准BP神经网络算法和附加动量法在沉降监测中的应用研究
李波1∗,柳华桥2,戴鑫3,贾志强4
(天津市测绘院,天津 300381)
在沉降监测工程实践中,由于采用的预测方法和项目沉降趋势的不同,预测结果的精度会有差异。而随着应用的不断深入,对现有算法进行改进以发挥算法的优势,成为目前预测算法研究的主流。在本文的研究中,编程实现了标准BP神经网络算法和附加动量法。通过研究学习率对标准BP神经网络算法的影响,确定学习率的大小。然后,研究了动量项对附加动量法收敛速度的影响,确定了动量项的取值。最后,对两种算法的稳定性和算法的效率以及预测精度等方面进行比较,探究两种算法的特点。
沉降监测;BP神经网络;附加动量法
1 引 言
人工神经网络是目前在变形监测领域广泛使用的预测方法。这种算法的优点是,对于复杂的非线性系统,能进行很好逼近,获得较高的拟合精度和预测精度。人工神经网络中使用最多的是BP神经网络。因为BP神经网络对变形的内部机制没有要求,可以在不清楚变形机制的情况下进行变形预测,使得这种方法得到了大量的研究和应用。
BP神经网络也有很多缺点,主要表现在:误差下降过程中,容易陷入局部极小值;误差收敛速度慢,耗时较长;发现变形机制的泛化能力一般;构建BP神经网络没有统一的原则[1]。本文在实现标准BP神经网络和附加动量的BP神经网络算法的基础上,对两种算法的稳定性和算法的效率以及对样本数据的预测精度等方面进行比较,得出有指导意义的结论,指导工程实践。
2 人工神经网络算法
2.1人工神经网络算法简介
人工神经网络算法模仿大脑神经元对刺激的应激机制,一般由3层组成:输入层、隐层、输出层。输入信号由输入层向隐层传输,经过隐层激活函数的作用,输出到输出层,再次经过激活函数的作用,得出网络的输出。通过正向学习获得的误差,利用梯度下降法进行反向传播,调整神经元之间的权值和阈值,使得输出的误差项达到要求,如图1所示。
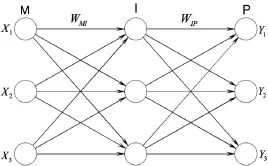
图1 BP神经网络结构示意图
2.2标准BP神经网络算法
设输入层的输入信号个数有M个,隐层有I个节点,输出层有P个节点。输入层的输入用XM表示,输入层和隐层之间的权值用WMI表示,隐层和输出层之间的权值用WIP表示。输出层的输出用YP表示。在样本的学习过程中,各层的输入和输出由下式计算:


那么,输出层第p个神经元的学习误差为:

2.3 附加动量的BP神经网络
所谓附加动量法是将权值调整量加上部分的上次权值调整量,作为一个整体,当作这次学习的权值调整量,这也是附加动量法和标准BP算法的区别所在。权值调整的公式如下所示:
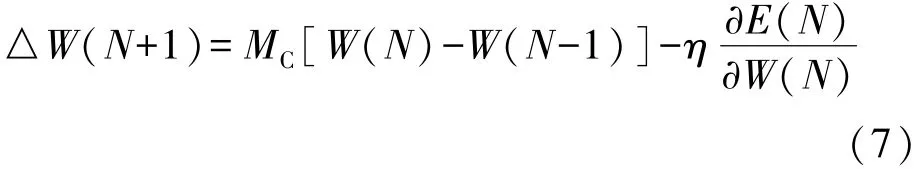
在上式中,MC表示加入的动量系数,N为训练的次数。
由上式可知,MC=0时,本次学习的权值调整量是按照梯度下降法确定。当网络的训练权值接近误差曲面的局部极小值时,局部梯度值变得很小。加入动量项可以避免陷入局部极小值的可能。
3 两种算法的比较与分析
3.1数据准备和网络结构设计
本文的样本数据采用天津市某高架桥桥墩沉降监测数据,通过传统水准测量的方法获得,样本共有24期。前20期为训练样本,后4期为预测样本。本文采用的样本数据如表1所示:

样本数据 表1
根据沉降数据的特征,将BP神经网络输入层和输出层的神经元数量均设置为1个,分别对应观测期数和沉降值。

由上述隐层节点数量的经验公式,将本文的隐层设计为单层,隐层节点数为4个。
3.2学习率对标准BP算法收敛速度的影响
权值的调整量是学习率和局部梯度的内积,因此学习率的大小直接影响权值调整量的多少。作者选取了5组学习率,分别是:0.10、0.25、0.40、0.55、0.70、0.85。针对每个学习率取值,刨除陷入局部极小值的情况,记录20次成功计算的迭代次数。实验结果如图2所示:
从图2可以得出,对于本文中所采取的数据而言,学习率较小时,迭代次数较多;随着学习率的增加,迭代次数减少。学习率取0.55时,迭代次数已经基本接近最小值。而当学习率取0.7以及0.85时,迭代次数并没有显著增加。但是当学习率取0.7以及0.85时, BP神经网络的陷入局部极小值以及发生震荡的次数明显增加。因此,对于本文中的样本数据,在后面的计算中,作者采用的学习率为0.55。
3.3算法的收敛速度比较
在本节中,作者采用算法的计算耗时作为评价算法收敛速度的指标。根据前面实验结果,学习率选取为0.55。根据样本数据计算时的收敛情况,动量系数取0.05。通过程序中内置的计时模块,输出每次计算的耗时,时间均四舍五入后取整到秒。使用的计算机为Dell M4800,处理器为i7-4810MQ,频率为2.80 GHZ,内存为8 G。作者分别进行了20次实验,计算结果如表2所示:

两种算法的耗时(单位/s) 表2
将表2以折线图的形式表示,如图3所示:
从图3可以看出,标准BP算法比附加动量算法的收敛速度快。但是在程序的实际计算过程中,标准BP算法陷入局部极小值的可能性很大,影响了算法的实用性。附加动量法相比标准BP算法,虽然收敛速度慢,但是避免了陷入局部极小值的情况,算法实用性更强。

图3 两种算法的收敛速度比较
3.4算法的稳定性比较
算法的稳定性是对每次计算耗时差异的量化指标。若算法每次计算的耗时差异较大,则这种算法的稳定性不高。否则,算法的稳定性就高。
在本节中,算法的稳定性使用下式计算:

上式中,N为计算的次数,XI是每次计算的耗时,为20次计算的平均耗时。根据表2中的实验数据,计算两种算法的稳定性。结果如表3所示:

两种算法的稳定性 表3
由表3可知,标准BP神经网络算法每次计算的耗时差异较小,算法稳定性较强。而附加动量法稳定性较差。但是,附加动量法避免了陷入局部极小的可能。
3.5算法的预测精度比较
利用本文采用的训练样本数据对预测样本数据进行预测。利用预测样本的残差的平方和来评价算法的预测精度。实验结果如表4所示:
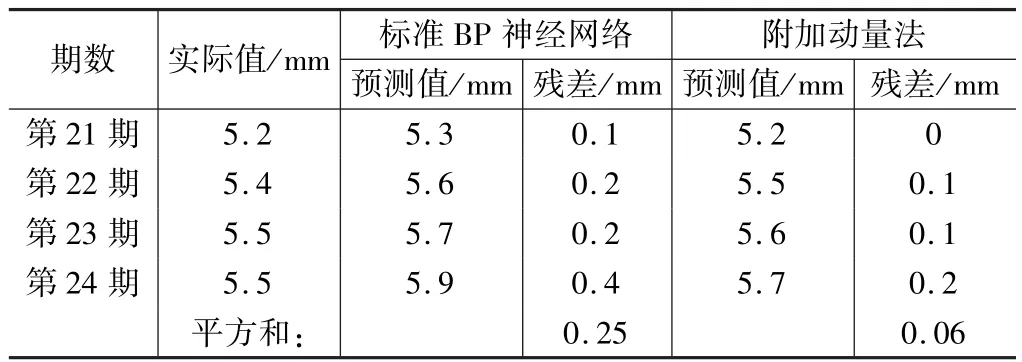
两种算法的预测精度比较 表4
根据表格中的统计数据,用折线图的形式表达,如图4所示:
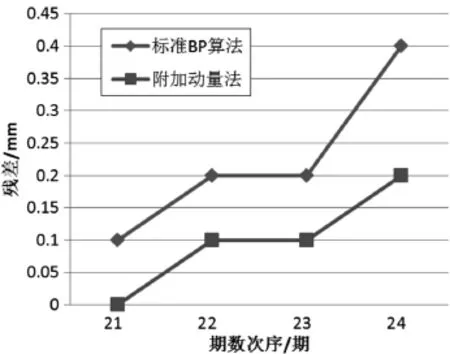
图4 两种算法的预测精度比较
表4中的预测值均取20次实验的结果得平均值。我们可以看出,标准BP算法预测值残差的平方和为0.25 mm2,附加动量法为0.06 mm2,附加动量法的预测精度优于标准BP算法。因此,对于本文采用的样本数据而言,附加动量法的预测精度更好一些。
4 结 语
(1)对于本文采用的样本数据而言,学习率较小时,BP神经网络的迭代次数较多;随着学习率的增加,迭代次数减少。学习率取0.55时,迭代次数已经基本接近最小值。而当学习率取0.7以及0.85时,迭代次数并没有显著增加。但是当学习率取0.7以及0.85时,BP神经网络的陷入局部极小值以及发生震荡的次数明显增加。
(2)标准BP算法比附加动量算法的收敛速度快。但算法陷入局部极小值的可能性很大,影响了算法的实用性。附加动量的BP算法收敛速度慢,但是避免了陷入局部极小值的情况。
(3)标准BP算法每次计算的耗时差异较小,算法稳定性较强。而附加动量法稳定性较差,但避免了陷入局部极小的可能。
(4)对于本文采用的训练样本而言,附加动量法的预测精度优于标准BP算法。
[1] Berman O,Krass D,Drezner Z,The Gradual Covering Decay Location Problem on a Network[J].European Journal of Operational Research,2003,151(3):474~480.
[2] 高颖,张双杰,王丽娟等.对改进的自适应BP算法中参数研究[J].合肥工业大学学报·自然科学版,2006,29(3):281~299.
[3] 黄世震,林淑玲.基于GSA-BP神经网络的压力传感器温度补偿[J].电子器件,2013,36(5):680~684.
[4] 候福均,吴祈宗.基于遗传算法和模拟退火算法优化神经网络的铁路营业里程预测[J].北京理工大学学报, 2004,24(3):247~250.
[5] Ding Shifei,Su Chunyang.An Optimizing BP Neural Network Algorithm Based on Genetic Algorithm[J].Spring, 011,36:153~162.
[6] 王英,曹军,孙丽萍.基于SAGA优化BP神经网络的木材含水率预测[J].控制理论与应用,2013,32(1):4~13.
[7] 董鹏,罗朝晖,伍洁等.BP神经网络的遗传模拟退火算法动态选址仿真[J].火力与指挥控制,2012,37(12):27~30.
Research on Application of Standard BP Neural Network Algorithm and Back-propagation With Momentum in the Practice of Engineering Settlement Monitoring
Li Bo1,Liu Huaqiao2,Dai Xin3,Jia Zhiqiang4
(Tianjin Institude of Surveying and Mapping,Tianjin 300381,China)
In the practice of engineering settlement monitoring,according to the difference of forecast methods and characteristics of the settlement trend,the accuracy of the prediction results will be different.With the deepening application,improving available algorithms to make the advantages of each algorithm a difference,has become the mainstream of research.In this paper,author implemented the standard BP neural network algorithm and back-propagation with momentum.By researching the effect of different learning rates for the standard BP neural network algorithm to determine the size of the learning rate.Then,author studied the effect of momentum on convergence speed of back-propagation with momentum,to determine the value of momentum.Finally,comparing the stability and efficiency of algorithms and forecast accuracy to explore the characteristics of the two algorithms.
settlement monitoring;BP neural network;back-propagation with momentum
1672-8262(2016)01-145-04
P258
B
∗2015—12—07
李波(1989—),男,硕士,助理工程师,主要从事工程测量等技术工作。

