CdH分子2∑+和2Π态的偶极矩及振动能级的理论研究
赵书涛,朱月强,张志国,李瑞,刘晓军,刘亚东
CdH分子2∑+和2Π态的偶极矩及振动能级的理论研究
赵书涛1,2,朱月强1,张志国1,李瑞3,刘晓军3,刘亚东3
(1. 阜阳师范学院 物理与电子工程学院,安徽 阜阳 236037;2. 中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;3. 齐齐哈尔大学 理学院,黑龙江 齐齐哈尔 101006)
采用含Davidson修正的多参考组态相互作用方法(MRCI+Q),对CdH分子最低的5个解离限对应的10个Λ-S态进行能量计算.计算结果表明,X2S+,B2S+,C2S+,42S+,A2P,22P为束缚态,14P,14S+,24S+,52S+为排斥态.计算了6个束缚态和7个二重态(2S+,2P)的振动能级、转动常数和偶极矩.理论计算结果与现有的实验值结果吻合较好.
CdH;偶极矩;振动能级;转动常数
Cd的化合物在环境污染中扮演重要的角色,已成为实验和理论上广泛关注的课题[1-2].作为最简单的Cd的化合物,CdH引起了实验和理论研究的极大兴趣.近些年,人们采用各种光谱技术和计算方法对其进行了电子结构和光谱性质的研究[3-4].早在上世纪20年代,Mulliken[5-6]对CdH分子的可见光/近紫外谱带进行了光谱观测,一系列的光谱研究主要集中在激发态(A2P,B2S+,C2S+)到基态X2S+的跃迁.Balfour[7-8]观测到了A2P-X2S+和B2S+-X2S+谱带,并通过振动和转动分析对这2个激发态的光谱参数进行了拟合.Nedelec和Khan[9-10]等人对C2S+-X2S+谱带和A2P-X2S+谱带进行了研究,发现了由C2S+态较高振动能级的预解离导致的光谱弥散现象和2S+-A2P态之间的微扰现象.吴小光[11]等人对A2P和X2S+的光谱及寿命进行测量,给出它们之间跃迁产生的具有转动结构的光谱.
对CdH分子较低电子态的光谱性质的理论研究也取得了一些成果.Balasubramanian[12]采用二阶组态相互作用方法对它的较低电子态的能量值和光谱常数进行了研究.李西平[13]等对分子进行了二级电子相关(SOCI)计算,给出了较低态的势能曲线和光谱参数.然而这2个理论研究并未考虑自旋-轨道耦合效应对光谱性质的影响.Shepler[14]等人采用高精度耦合簇(CCSD(T))方法对X2S+进行了研究,对较高激发态并未涉及.李瑞[15]等人采用考虑自旋-轨道耦合效应的MRCI方法计算了较低电子态的电子结构和光谱参数.虽然一系列的理论研究计算给出了CdH分子的电子结构和光谱性质,但关于该分子的偶极矩和振动能级及转动常数的信息依然非常有限.
本文采用高精度从头算方法对CdH分子的较低电子态的势能曲线和偶极矩进行研究.基于Λ-S态势能曲线的结果,拟合给出束缚态的振动能级和转动常数.
1 计算方法
应用MOLPRO2010程序包[16]中的从头计算方法精确计算了CdH分子的电子结构.计算中对Cd原子和H原子分别采用aug-cc-pwCVTZ-dk[17]和aug-ccpVTZ-DK[18]基组.由于软件包的局限,在理论计算时,CdH分子的Cµv群得由C2v群代替.两者之间的对应关系为:Σ+=A1,Π= B1+B2,Δ= A1+A2和Σ-=A2.在核间距为0.12~0.8 nm区间,采用态平均的完全活性空间自洽场(CASSCF)[19-20]方法对CdH的较低电子态进行计算.在计算中,选取Cd的5s5p6s6p和H的1s原子轨道对应的9个分子轨道(5a1,2b1,2b2)作为活性空间.采用MRCI+Q方法[21-22]计算了CdH分子的10个Λ-S态的能量值,计算中,Cd的内壳层电子1s22s22p63s23p63d104s24p6被放入冻芯轨道,而它的4d105s2和H原子的1s1电子参与内壳层-价壳层关联效应计算,总共考虑了13个电子的关联效应.
基于计算的Λ-S态势能曲线,利用LEVEL程序包[23]求解CdH分子的一维核运动Schrödinger方程来获得束缚态(X2S+,B2S+,C2S+,42S+,A2P,22P)的振动能级和转动常数.
2 研究结果
2.1 离解限和电子态
CdH分子最低5个离解限为Cd(1Sg)+H(2Sg),Cd(3Pu)+H(2Sg),Cd(1Pu)+H(2Sg),Cd(3Sg)+H(2Sg),Cd(1Sg)+H(2Sg),由离解限的原子态可以推导出对应的分子态.Cd,H原子态和CdH分子态分属为SO(3)和 Cµv群,两者对应关系为:Sg®Σ+,Pu®Σ++Π.
(1)
(2)
(3)
(4)
通过式(1),可以推导出第1,5离解限Cd(1Sg)+H(2Sg),Cd(1Sg)+H(2Sg)对应的电子态都为2S+;由式(2),可以得到第2离解限Cd(3Pu)+H(2Sg)对应的电子态为2,4S+,2,4P;由式(3)得出第3离解限Cd(1Pu)+H(2Sg)对应的电子态为2S+,2P;由式(4)给出第4离解限Cd(3Sg)+H(2Sg)对应电子态2,4S+.
CdH分子的5个离解限对应10个电子态,在这些电子态中涉及二重态的有7个:2S+(5),2P(2);四重态的有3个:4S+(2),4P.
2.2 偶极矩
在核间距0.12~0.8 nm上取51个点(在0.12~0.3、0.3~0.4、0.4~0.8 nm上,分别每0.005,0.01,0.1 nm取一点),采用MRCI+Q方法对Cd(1Sg)+H(2Sg),Cd(3Pu)+H(2Sg),Cd(1Pu)+H(2Sg),Cd(3Sg)+H(2Sg),Cd(1Sg)+H(2Sg)5个离解限对应的10个L-S态的能量进行计算,结果表明束缚态都为二重态.计算得到的第2,3,4,5离解限与第1离解限的能量差为30 681,44 375,50 442,52 387 cm-1,与实验值[24]31 246,43 692,51 483,53 310 cm-1的偏差分别为1.8%,1.5%,2%,1.7%.理论结果与实验值偏差较小,表明理论计算的准确性.讨论二重态2S+和2P的偶极矩见图1.

图1 MRCI+Q 计算的CdH 分子的二重态偶极矩曲线
从图1可以看出,所有的电子态的偶极矩在核间距很大的区域都趋于零,表明它们的离解产物都为中性原子,这与上述5个离解限的理论推导结果相吻合.X2S+在平衡位置0.176 nm附近成键区域的偶极矩接近于零,表明基态具有共价性特点.A2P在平衡位置0.167 nm附近的偶极矩绝对值为1.90 Debye,表明电子态在此区域具有部分离子性特点.B2S+平衡位置0.241 nm附近和C2S+右侧的平坦势阱区域的偶极矩具有较大值,表明电子态具有离子性特点,这2个电子态在0.15 nm附近发生避免交叉,导致偶极矩急剧变化,发生极性反转.C2S+与42S+具有相同对称性,在0.2~0.3 nm区域存在避免交叉作用,导致它们的离子性特征从一个态转移到另外一个态.52S+的偶极矩在很大区域内都不为零,具有离子性特征.22P态在0.2 nm附近偶极矩急剧变化,表明与上一个2P态有避免交叉现象,在核间距大于0.24 nm时,偶极矩接近于零,说明具有共价性特点.
在Λ-S束缚态(X2S+,B2S+,C2S+,42S+,A2P,22P)的势能曲线基础上,借助LEVEL程序包对CdH分子核运动的薛定谔方程进行求解,拟合出它们的振动能级和转动常数(见表1).
表1 X2S+,B2Σ+,C2Σ+,42Σ+和A2Π,22Π的振动能级和转动常数 cm-1
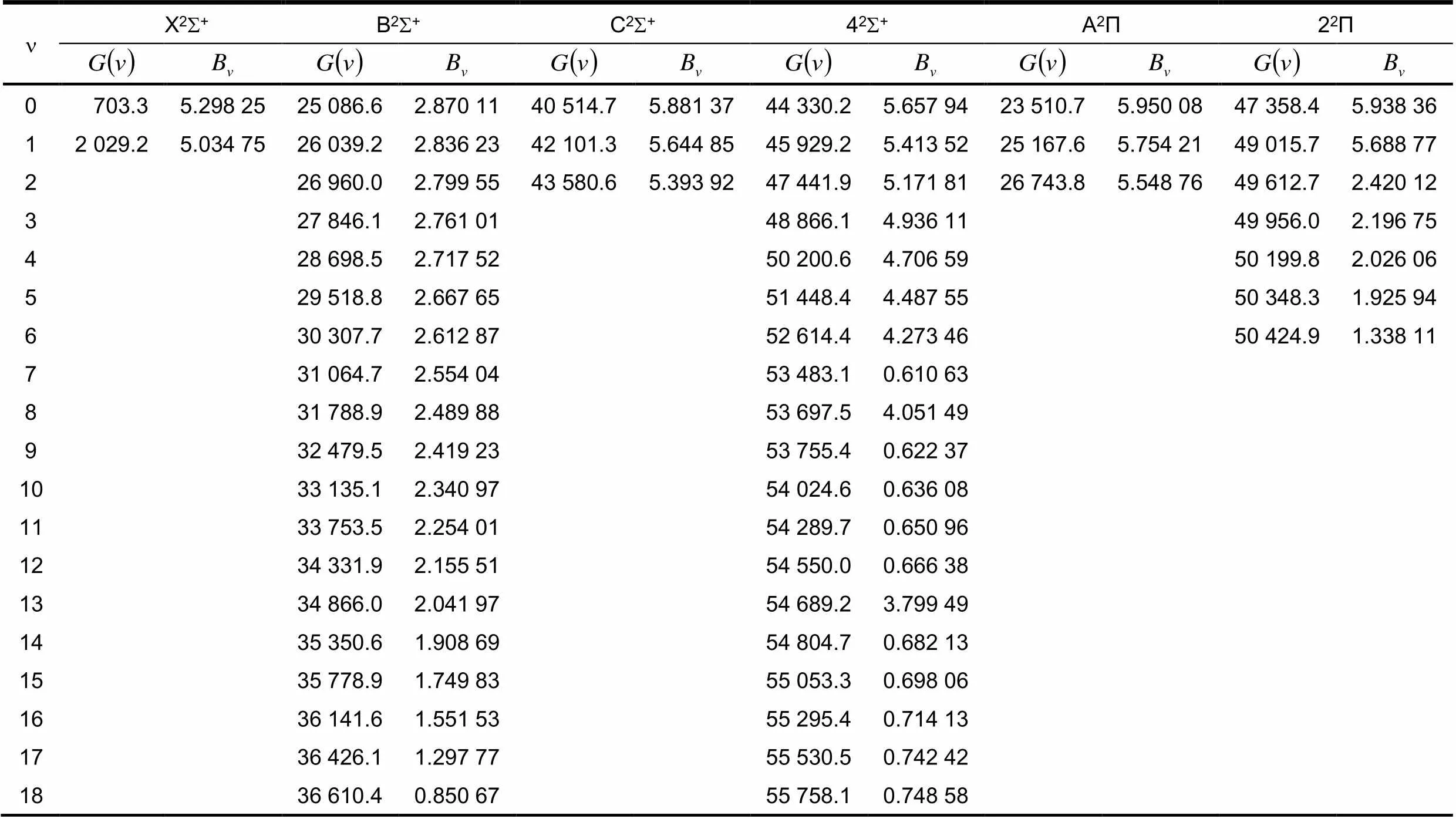
表1 X2S+,B2Σ+,C2Σ+,42Σ+和A2Π,22Π的振动能级和转动常数 cm-1
n X2S+B2S+C2S+42S+A2Π22Π 0703.35.298 2525 086.62.870 1140 514.75.881 3744 330.25.657 9423 510.75.950 0847 358.45.938 36 12 029.25.034 7526 039.22.836 2342 101.35.644 8545 929.25.413 5225 167.65.754 2149 015.75.688 77 226 960.02.799 5543 580.65.393 9247 441.95.171 8126 743.85.548 7649 612.72.420 12 327 846.12.761 0148 866.14.936 1149 956.02.196 75 428 698.52.717 5250 200.64.706 5950 199.82.026 06 529 518.82.667 6551 448.44.487 5550 348.31.925 94 630 307.72.612 8752 614.44.273 4650 424.91.338 11 731 064.72.554 0453 483.10.610 63 831 788.92.489 8853 697.54.051 49 932 479.52.419 2353 755.40.622 37 1033 135.12.340 9754 024.60.636 08 1133 753.52.254 0154 289.70.650 96 1234 331.92.155 5154 550.00.666 38 1334 866.02.041 9754 689.23.799 49 1435 350.61.908 6954 804.70.682 13 1535 778.91.749 8355 053.30.698 06 1636 141.61.551 5355 295.40.714 13 1736 426.11.297 7755 530.50.742 42 1836 610.40.850 6755 758.10.748 58
对应6个束缚态,通过理论计算分别找到2,19,3,23,3和7个振动能级,出于篇幅考虑,对于42S+电子态则只给出了前19个振动能级.A2P,B2S+,C2S+,42S+电子态的零振动能级与基态X2S+的零振动能级的能量差值为22 807,24 383,39 811,43 626 cm-1与实验值[25]22 776,24 749,40 314,44 136 cm-1的偏差分别为0.1%,1.5%,1.2%,1.2%,表明了理论计算的可靠性.基态X2S+的= 0,1的转动常数为5.298,5.035 cm-1与实验值[3]915.325,5.063 cm-1吻合较好.其它电子态的振动能级和转动常数的实验值尚无报到.
因此,本文的理论计算结果可以为后续的实验提供参考.
3 结论
对CdH分子的最低的5个离解限Cd(1Sg)+H(2Sg),Cd(3Pu)+H(2Sg),Cd(1Pu)+H(2Sg),Cd(3Sg)+H(2Sg),Cd(1Sg)+H(2Sg)的10个L-S电子态进行了MRCI+Q的理论计算.关于二重态2S+和2P的偶极矩的计算表明,基态X2S+在成键区域具有共价性特征;B2S+,C2S+和42S+电子态存在由于避免交叉现象导致偶极矩急剧变化的特点.对束缚态X2S+,B2S+,C2S+,42S+,A2P,22P的振动能级和转动常数的计算表明,A2P,B2S+,C2S+,42S+电子态与基态X2S+的零振动能级能量差值及基态X2S+的= 0,1的转动常数都与实验值吻合很好.预测的其它激发态的振动能级和转动常数可以为后续的实验提供参考.
[1] Koren,Kump P.Influence of CdCl2and CdSO4supplementation on Cd distribution and ligand environment in leaves of the Cd hyperaccumulator Noccaea(Thlaspi)praecox[J].Plant and Soil,2013,370(1-2):125,148
[2] Küpper H,Andresen E.Mechanisms of metal toxicity in plants[J].Metallomics,2016, 8(3):269-285
[3] Shayesteh A,Le Roy R J,Varberg T D,et al.Multi-isotopologue analyses of new vibration rotation and pure rotation spectra of ZnH and CdH[J].J Mol Spectrosc,2006,237(1):87-96
[4] Eliav E,Kaldor U,Hess B A.The relativistic Fock-space coupled-cluster method for molecules:CdH and its ions[J].J Chem Phys,1998,108(9):3409-3415
[5] Mulliken R S.Electronic States and Band Spectrum Structure in Diatomic Molecules.VII.2P®2S and2S®2P Transitions[J].Phys Rev,1928,32(3):388-416
[6] Mulliken R S.Systematic Relations between Electronic Structure and Band-Spectrum Structure in Diatomic Molecules.II.The ZnH,CdH and HgH Molecules and their Spectra[J].Proc Natl Acad Sci U S A,1926,12(3):151-158
[7] Balfour W J,Ram R S.The B2Σ+state of cadmium deuteride[J].J Mol Spectrosc,1987,121(1):199-208
[8] Balfour W J.The A2Π- X2Σ+Emission System of Cadmium Deuteride[J].Phys Scr,1982,25(2):257-267
[9] Nedelec O,Majournat B,Dufayard J.Configuration mixings and line intensities in CdH and HgH A2Π-X2Σ+transitions[J].Chem Phys,1989,134(1):137-148
[10] Khan M A.A New Band System in CdH and CdD[J].Proc Phys Soc,1962,80(6):1264-1268
[11] 吴小光,张培林,赵朔嫣.CdH分子基态X2Σ+和激发态A2П光谱和寿命测量[J].光学学报,1993,13(9):769-774
[12] Balasubramanian K.The low lying states of the secondrow transition metal hydrides(YH CdH)[J].J Chem Phys,1990,93(11):8061-8072
[13] 李西平,戴树珊.CdH分子的量子化学研究[J].物理化学学报,1996,12(6):508-512
[14] Shepler B C,Peterson K A.Chemically Accurate Thermochemistry of Cadmium:An ab Initio Study of Cd + XY(X = H,O,Cl,Br;Y = Cl,Br)[J].J Phys Chem A,2006,110(44):12321-12329
[15] Li R,Zhai Z,Zhang X M,et al.Spin orbit all-electron configuration interaction study on the electronic structure and radiative lifetimes of low-lying excited states of CdH[J].Chem Phys Lett,2014,599:51-56
[16] Werner H J,Knowles P,Knizia G,et al.MOLPRO version 2010 1,a package of ab initio programs[EB/OL].[2010].http://www.molpro.net
[17] Peterson K A,Figgen D,Dolg M,et al.Energy-consistent relativistic pseudopotentials and correlation consistent basis sets for the 4d elements Y Pd[J].J Chem Phys,2007,126(12):124101
[18] JrTHD.Gaussian basis sets for use in correlated molecular calculations.I.The atoms boron through neon and hydrogen[J].J Chem
Phys,1989,90(2):1007-1023
[19] Werner H J,Knowles P J.A second order multiconfiguration SCF procedure with optimum convergence[J].J Chem Phys,1985, 82(11):5053-5063
[20] Knowles P J,Werner H J.An efficient second-order MCSCF method for long configuration expansions[J].Chem Phys Lett,1985, 115(3):259-267
[21] Knowles P J,Werner H J.An efficient method for the evaluation of coupling coefficients in configuration interaction calculations[J].Chem Phys Lett,1988,145(6):514-522
[22] Werner H J,Knowles P J.An efficient internally contracted multiconfiguration reference configuration interaction method[J].J Chem Phys,1988,89(9):5803-5814
[23] Le Roy R J.LEVEL8.0:A computer program for solving the radial Schrödinger equation for bound and quasibound levels[J].Chem Phys Res Rep CP-663,University of Waterloo:Ontario,Canada,2007
[24] Moore C E.Atomic Energy Levels[M].National Bureau of Standard:Washington,DC,1971
[25] Huber K P,Herzberg G.Molecular Spectra and Molecular Structure:IV.Constants of diatomic molecules[M].New York:Van Nostrand Reinhold,1979
Theoretical study on the dipole moments and vibrational levels of the2S+and2Pstates of CdH molecule
ZHAO Shu-tao1,2,ZHU Yue-qiang1,ZHANG Zhi-guo1,LI Rui3,LIU Xiao-jun3,LIU Ya-dong3
(1. School of Physics and Electronic Engineering,Fuyang Normal University,Fuyang 236037,China;2. Changchun Institute of Optics,Fine Mechanics and Physics,Chinese Academy of Sciences,Changchun 130033,China;3. School of Science,Qiqihar University,Qiqihar 161006,China)
The multi-reference configuration interaction including Davidson correction(MRCI+Q)calculations were performed for the ten Λ-S states correlating with the first five dissociation asymptotes of CdH molecule. The computed results show that X2S+,B2S+,C2S+,42S+,A2P,22Pare the bound states,while the 14P,14S+,24S+,52S+are the repulsive states. The vibrational levels and rotational constants of the six bound states and the dipole moments of these seven doublet states(2S+,2P)were determined,which are in good accordance with the previous experimental values.
CdH;dipole moment;vibrational level;rotational constant
1007-9831(2016)09-0042-04
O561
A
10.3969/j.issn.1007-9831.2016.09.012
2016-07-10
国家自然科学基金项目(11604052);长春光机所国家光栅工程中心开放基金项目(K201601);黑龙江省自然基金项目(A2015010);黑龙江省教育厅青年创新人才培养计划资助项目(UNPYSCT-2015095)
赵书涛(1982-),男,安徽阜阳人,讲师,博士,从事原子与分子物理、光学的研究.E-mail:zhaosht2013@sina.com

