基于交叉梯度约束的地震初至纵波与瑞雷面波联合反演

傅磊， 刘四新

吉林大学 地球探测科学与技术学院， 长春 130026



基于交叉梯度约束的地震初至纵波与瑞雷面波联合反演

傅磊， 刘四新

吉林大学 地球探测科学与技术学院， 长春 130026

本文提出了一种初至纵波(P波)与瑞雷面波的交叉梯度联合反演策略.通过对初至P波进行全波形反演可以获得近地表P波速度结构；通过对仅含瑞雷面波信息的地震数据转换到频率-波数域进行加窗振幅波形反演(Windowed-Amplitude Waveform Inversion，w-AWI)可获得近地表横波(S波)速度结构.在二者反演的目标函数中均加入P波速度和S波速度的交叉梯度作为正则化约束项，使得在反演过程中P波速度和S波速度相互制约，相互约束，从而实现对地震初至P波与瑞雷面波的联合反演.数值模拟结果表明交叉梯度联合反演可以提高S波速度反演分辨率，而P波速度反演结果并没有得到提高.实际资料的反演结果表明，交叉梯度联合反演能够获得更加可信的近地表速度结构.

初至纵波； 瑞雷面波； 交叉梯度； 联合反演

1 引言

在勘探地震的偏移成像中，近地表速度(P波速度和S波速度)结构(刘伊克等, 2001)的精确度制约着深层地质结构的构建.目前为止，大多数面波反演(Xia et al., 1999; 石耀霖和金文, 1995; 胡家富等, 1999; 李明明和何玉梅, 2011)基于层状模型假设，这一假设在实际复杂的地质环境中并不适用.为了克服这个层状模型假设，许多研究人员尝试采用波形反演的思路对面波进行反演.Schäfer等(2013)采用全波形反演方法对两个实际数据进行测试，结果表明反演过程收敛速度极慢以及反演结果往往陷入局部最小值.Solano等(2013)提出了一种振幅波形反演(Amplitude Waveform Inversion)的方法，其目标函数为观测数据振幅谱与预测数据振幅谱的最小二范数，而传统的全波形反演(Tarantola,1984; Pratt et al., 1998; Virieux and Operto, 2009)的目标函数为观测数据与预测数据的最小二范数，结果表明振幅波形反演具有更好的收敛性质.这是因为传统的全波形反演匹配的是所有波形，而振幅波形反演只匹配振幅谱，振幅谱仅仅是所有波形信息中的一部分，这种简化的数据(Luo and Schuster, 1991a, 1991b)使得振幅波形反演具有更快的收敛速度和更好的收敛效果.Solano等(2014)提出了一种加窗振幅波形反演方法(Windowed-Amplitude Waveform Inversion)，与振幅波形反演相比，该方法更加稳定.然而与传统全波形反演相比，振幅波形反演是以牺牲分辨率为代价的.为了部分恢复振幅波形反演丢失的分辨率，本文提出了一种初至P波与瑞雷面波的交叉梯度联合反演(于鹏等, 2009; 彭淼等, 2013; 李兆祥等, 2015)方法，采用交叉梯度同时作为初至P波反演和瑞雷面波加窗振幅波形反演的约束项，将分辨率较低的瑞雷面波振幅波形反演与高分辨率的P波波形反演结合起来，可以获得更高分辨率的S波速度结构.

地球物理数据的联合反演可以分为两大类.第一类是基于不同参数之间的岩石物理关系，例如饱和度和孔隙度(Hoversten et al., 2006)，电导率和介电常数(Kowalsky et al., 2005).例如，P波和S波速度之间的关系是依赖于介质属性的.Castagna等(1985)指出，在砂岩中P波与S波比约为1.5～1.7，在页岩中该比值大于2.这就意味着在联合反演中，采用不同参数之间错误的经验关系可能会带来严重的耦合误差.

第二类联合反演利用不同参数之间的结构相似性，同一地质模型可以用不同的物性参数来描述，例如密度、P波速度、电导率等，这些参数存在着结构相似性.Gallardo和Meju(2003)采用交叉梯度联合反演方法成功地对直流电法和地震走时数据进行了反演.Colombo和De Stefano(2007)等利用交叉梯度联合反演方法同时对地震、重力和大地电磁数据进行了反演.本文采用第二类联合反演策略对初至地震P波和瑞雷面波进行交叉梯度联合反演.

对于初至纵波，本文采用全波形反演获得地下P波速度结构，采用加窗振幅波形反演方法对瑞雷面波进行反演，同时采用P波速度和S波速度的交叉梯度作为二者的约束项.结果显示，与单独的瑞雷面波振幅波形反演相比，交叉梯度联合反演的S波速度具有更高的精度.本文第2节和第3节将分别给出交叉梯度联合反演的方法原理以及数值模拟结果.之后，将该联合反演方法应用于实际数据.最后是结论.

2 方法原理

对于地震数据，初至P波可以通过求解二维常密度声波方程来进行模拟，

(1)

其中v是纵波速度，p(x,t)是压力场，f(x,t)是震源项.

另一方面，瑞雷面波可以通过求解弹性波方程进行模拟获得，

(2)

其中ρ是密度，ui是第i个位移分量，cijkl是刚度矩阵，si是震源项.

2.1 交叉梯度

交叉梯度的定义为两个模型参数梯度的叉积：

(3)

其中mP代表P波速度，而mS代表S波速度.交叉梯度正则项是基于这样的事实，当两个模型参数的交叉梯度达到最小化时，它们的结构相似度将达到最大化.如果在P波和S波速度中存在相同的边界，且该边界的位置和方向一致，那么它们的交叉梯度将等于零.

对于二维问题，方程(3)可以改写为：

(4)

如图1a为P波速度模型，波速从左到右逐渐增大；图1b为S波速度模型，一个低速方形异常体、一个高速圆形异常体及一个高速方形异常体嵌于一均匀背景速度模型；图1c为二者的交叉梯度值.以左侧低速异常体为例，虽然在S波速度中四条边界处的梯度值均不为零；然而在P波速度中低速方形所在位置的左、右边界处的梯度与S波速度中对应的梯度平行，故而交叉梯度值为零，仅在上下边界处其交叉梯度值不为零.

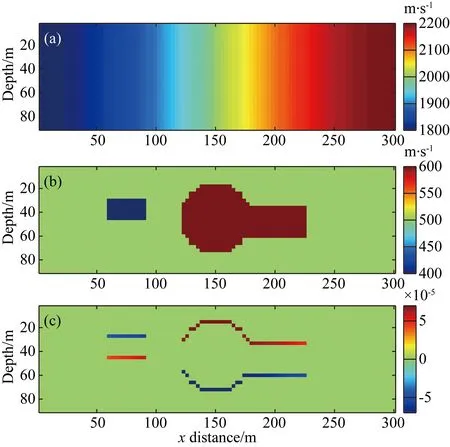
图1 (a)P波速度模型，(b)S波速度模型，(c)相应P波速度与S波速度的交叉梯度Fig.1 (a) P-wave velocity model, (b) S-wave velocity model, (c) Corresponding cross-gradients of P-wave velocity and S-wave velocity models

2.2 初至P波全波形反演

波动方程波形反演的目标函数为：

‖Δdrs‖2,

(5)

其中Δdrs=dcal(xr,xs)-dobs(xr,xs)是初至P波残差，它表示为预测数据与观测数据之差.对于P波速度，它可以通过任何一种梯度类方法进行迭代更新，例如通过共轭梯度(Hestenes and Stiefel, 1952; 胡祖志, 2006)方法对P波速度进行更新：

(6)

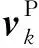
(7)

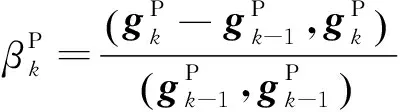
(8)

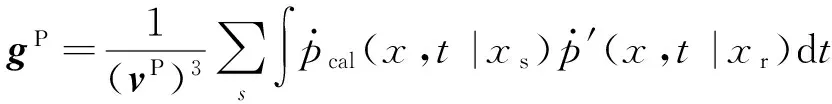
(9)

其中，

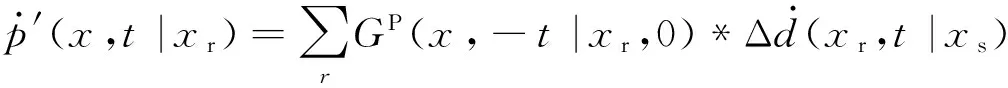
(10)

2.3 瑞雷面波加窗振幅波形反演

加窗振幅波形反演(Solano et al., 2014)是在全波形反演的基础上衍生出来的，它的目标函数为：

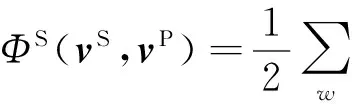
(11)

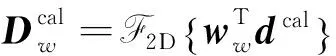
(12)

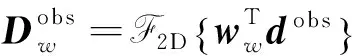
(13)

(14)

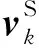
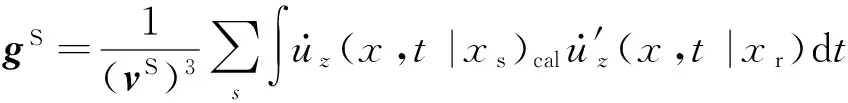
(15)

其中

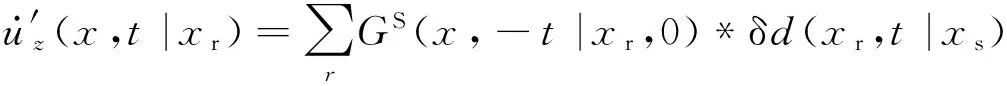
(16)

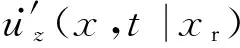
δd(xr,t|xs)=

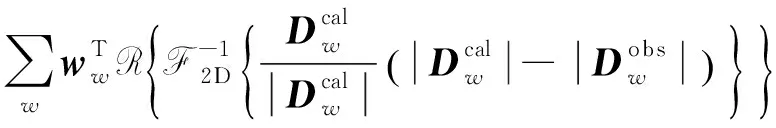
(17)

2.4 交叉梯度联合反演目标函数及梯度

为了提高反演结果的精度，本文将初至P波与S波速度进行联合同步反演，对于初至P波，其全波形联合反演目标函数为：

(18)

同理对于瑞雷面波，其加窗振幅波形联合同步反演的目标函数则为：

ΦS(vS,vP)=

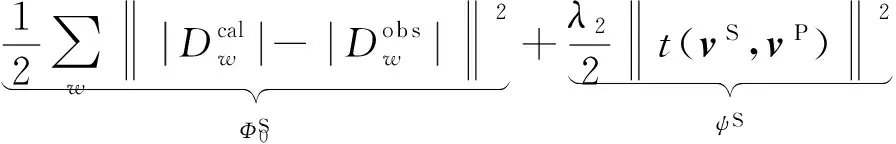
(19)

其中λ1和λ2分别为各自的正则化系数，当这两个正则化系数同时置为零时，方程(18)和(19)退化为无耦合的单独反演方程.对于交叉梯度联合反演，关键问题是计算目标函数(18)和(19)分别对P波速度和S波速度的偏导，即获得各自的梯度.注意到交叉梯度联合反演目标函数均包含两项，原始目标函数项和正则约束项，而原始目标函数对应的梯度已知，故关键问题是求取正则约束项分别对P波速度和S波速度的梯度，根据Hu等(2009)，经过数学推导，正则项的梯度分别表示为：

(20)

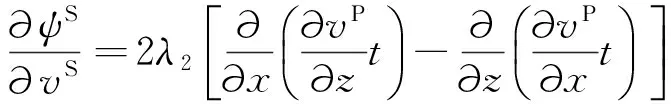
(21)

3 数值实验

3.1 目标函数形态

全波形反演是病态的非线性反演问题，非线性、跳周、子波估计不准等现象往往使得波形反演问题陷入局部最小值.本文选取加窗振幅波形反演对瑞雷面波进行反演，是因为与全波形反演相比，它更容易收敛到全局最小值.为了比较全波形反演、振幅波形反演及加窗振幅波形反演三种目标函数的形态，首先构建一简单模型如图2所示，图2为S波速度模型，一条带状异常体速度vS1嵌于均匀背景速度vS0中，真实速度模型和初始速度模型同时取决于vS1和vS0.假设真实背景速度大小为800 m·s-1，真实异常体速度大小为960 m·s-1；通过改变vS1和vS0获得不同的初始模型，其中vS1的变化范围为400～1400 m·s-1，vS0的变化范围为600～1400 m·s-1.同时P波速度设为2000 m·s-1，密度设为1000 kg·m-3.图中红色星号代表震源所在位置，采用中心频率为20 Hz的雷克子波作为震源；检波器均匀分布于地表.图3为三种不同目标函数的形态，十字虚白线交叉点为真模型；图3a为全波形反演目标函数形态；图3b为振幅波形反演目标函数形态；图3c为加窗振幅波形反演目标函数形态，可见加窗目标函数具有最宽的全局最小范围，最容易收敛到全局最小.相比于初至P波，瑞雷面波具有更强的非线性性质，故而本文对瑞雷面波采用加窗振幅波形反演方法；而对初至P波采用全波形反演方法.

3.2 数值算例

首先将交叉梯度联合反演方法应用于简单数值模型图4.其中图4a是P波速度模型，图4b为S波速度模型.该模型包括三层岩层，从地表到深部其速度逐渐递增，且不同岩层之间界面为不规则界面.模型被离散为30×120的等体积立方体网格，网格间距为3 m.图中红色X表示震源所在位置，其间距为6 m；地表均匀布设120个检波器，检波器间距为3 m.源子波为中心频率为20 Hz的雷克子波.初始速度模型见图5，它是将真实速度模型进行50次高斯滤波圆滑获得.

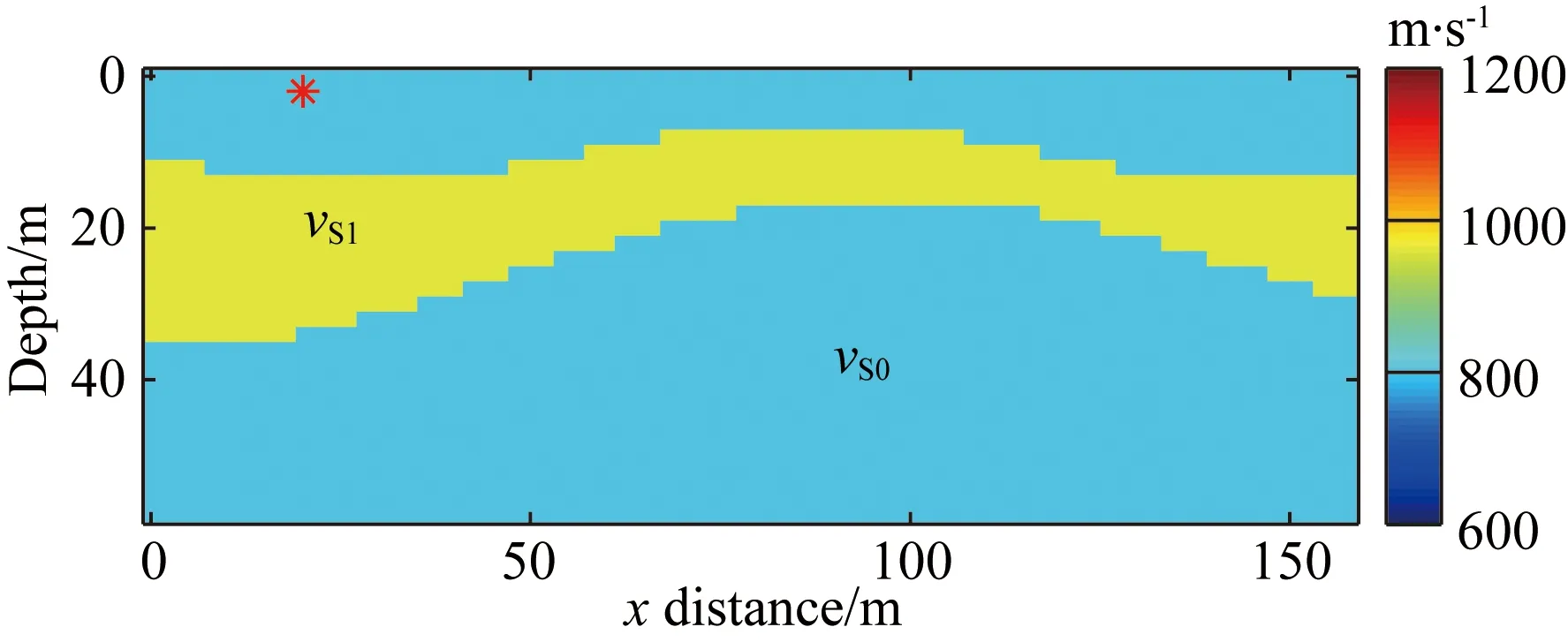
图2 用于计算目标函数形态的S波速度模型，v S0代表背景速度，v S1代表异常体速度Fig.2 S velocity models used to compute different target function shapes. vS0 represents background S velocity. vS1 represents abnormal S velocity

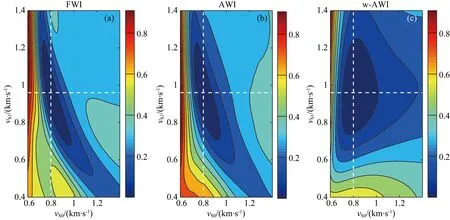
图3 不同方法归一化目标函数(a) 全波形反演； (b) 振幅波形反演； (c) 加窗振幅波形反演.Fig.3 Normalized objective functions by different methods

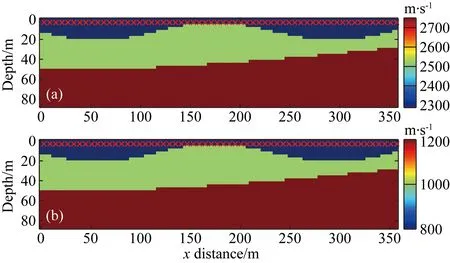
图4 真实速度模型其中红色X代表震源所在位置.(a) P波速度模型；(b) S波速度模型.Fig.4 Real velocity modelsRed X indicates source location. (a) P-wave velocity model; (b) S-wave velocity model.

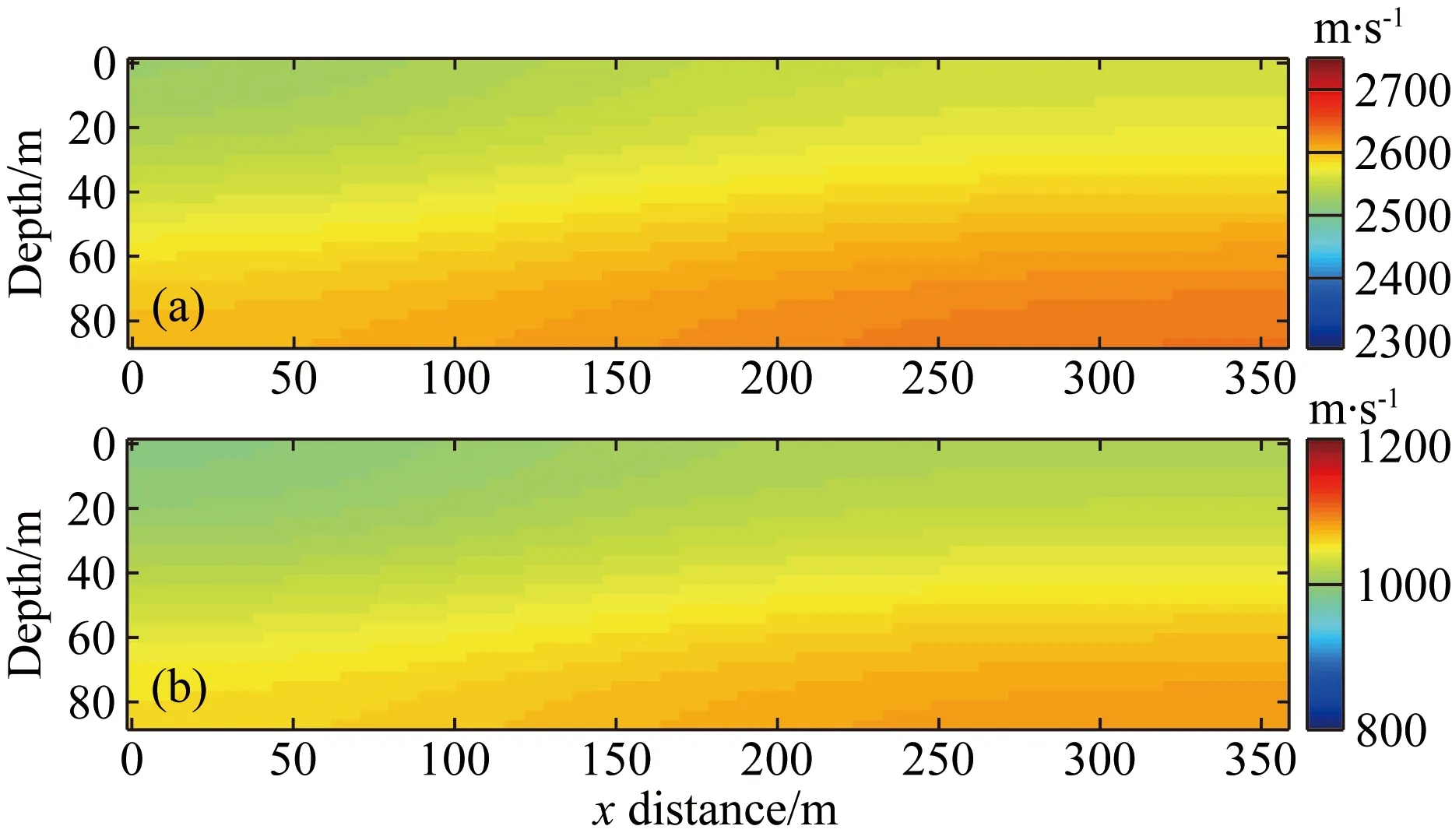
图5 (a) 初始P波速度模型， (b) 初始S波速度模型Fig.5 Initial P-wave velocity model (a) and S-wave velocity model (b)

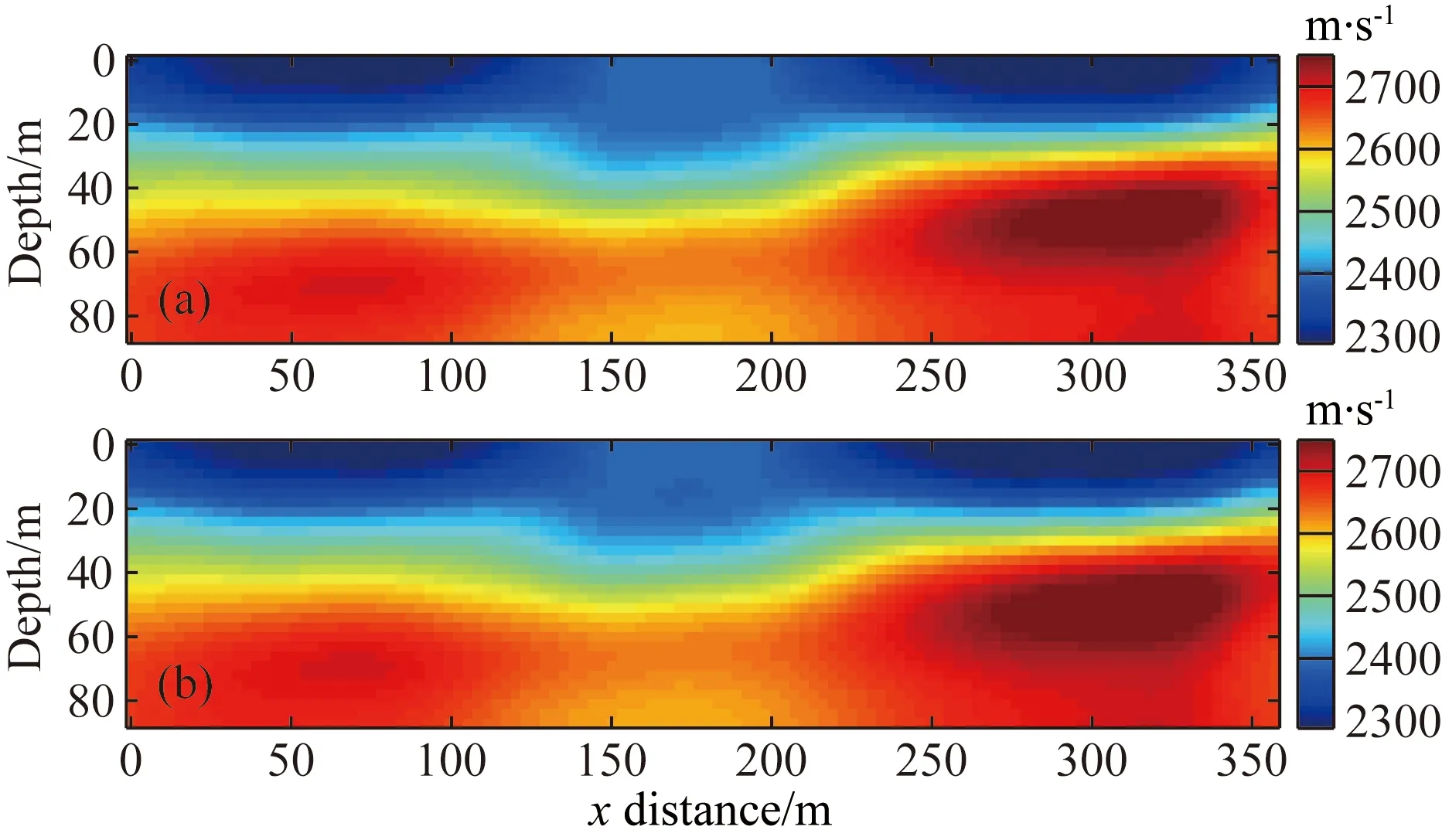
图6 初至P波全波形反演结果(a) 单独反演第10次迭代P波速度结果； (b) 联合反演第10次迭代P波速度结果.Fig.6 Full-waveform inversion results of first arrival P waves(a) Single inversion of P-wave velocity after 10 iterations; (b) Joint inversion of P-wave velocity after 10 iterations.

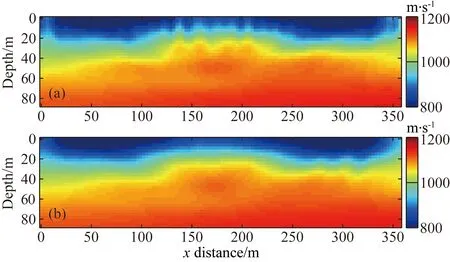
图7 瑞雷面波反演结果(a) 单独反演第10次迭代S波速度结果； (b) 联合反演第10次迭代S波速度结果.Fig.7 Inversion results for Rayleigh waves(a) Single inversion of S-wave velocity after 10 iterations; (b) Joint inversion of S-wave velocity after 10 iterations.

图6a是经过10次迭代后单独反演的P波速度结果，由图可知，P波反演结果中基本可以识别出三层岩层，其中浅层形态与真实模型吻合较好；底层高速层的形态及反演结果与真实模型基本一致；中间层的形态与真实模型基本一致，然而其反演结果与真实模型存在一定误差.图6b是经过10次迭代后交叉梯度联合反演P波速度结果，其结果同样并没有得到提高.

图7所示为经过10次迭代反演S波速度结果.图7a为单独反演S波速度结果，由图可知，浅层速度结构刻画得较好，浅层与中间层的界面与真实模型基本吻合，但是中间层及底层的反演结果与真实模型存在较大误差.这是因为瑞雷面波的穿透深度仅为其波长的1/3至1/2，而这里浅层的速度为800 m·s-1，对应的波长为40 m，故而其探测深度应在20 m范围内.图7b为交叉梯度联合反演S波速度结果，可以看到：交叉梯度联合反演S波速度结果中，浅层界面的连续性好于单独反演结果.

4 实际资料

4.1 数据采集及预处理

此二维地震勘探的目的是为了探明地下某隐伏断层在地表的位置.该二维地震剖面包括240个垂直分量检波器，检波器间距为5 m.时间采样率为1 ms，记录长度为3 s，每个地震记录进行32次叠加，总共240炮地震记录.图8a，8b，8c，8d分别为偏移距为10 m，30 m，50 m，70 m的共偏移距地震剖面.通过对比不同共偏移距剖面，我们认为该隐伏断层可能位于第55炮所在位置，即位于水平位置275 m处，即如图中红色虚线所示.故本文选取第21炮至第81炮地震记录进行反演.

图9a为第21炮原始地震记录，图中红色虚线所示为初至P波，而蓝色虚线所示为瑞雷面波.通过对两条虚线的斜率进行估算，可以得到近地表的P波速度和S波速度分别约为2900 m·s-1和460 m·s-1.在数据预处理之前，首先手动提取初至P波和瑞雷面波走时，提取的走时将用于后续提取初至P波和瑞雷面波波形.

数据预处理的第一步是选取3～50 Hz滤波器对原始数据进行带通滤波；其次对数据进行三维到二维转换及几何扩散校正；第三步去除坏道并采用POCS(Projection onto Convex Sets)(Abma and Kabir, 2006)对缺失道进行数据插值；第四步在时间域对数据进行插值，使得时间采样率满足正演模拟需求；最后切除近偏移距地震道以及根据提取的走时将初至P波和瑞雷面波提取出.经过预处理后的数据如图9b所示.

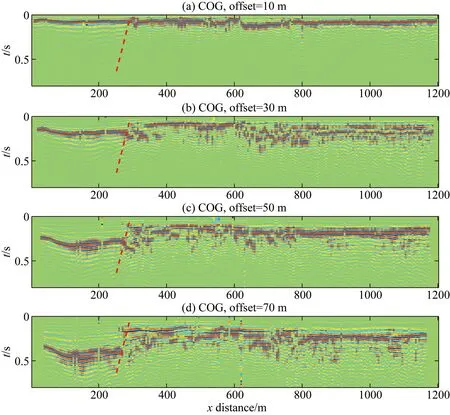
图8 经过带通滤波及道内归一化后的共偏移距剖面红色虚线指示断层的可能位置. (a) 偏移距为10 m； (b) 偏移距为30 m； (c) 偏移距为50 m； (d) 偏移距为70 m.Fig.8 Common offset sections from processed data after bandpass filtering and trace normalizationRed dash lines indicate the possible fault location.

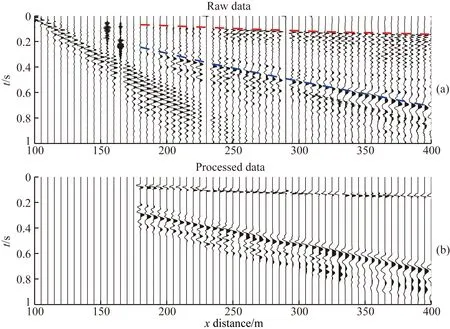
图9 (a) 第21炮原始数据记录，红色虚线为提取的P波走时，蓝色虚线为提取的瑞雷面波走时； (b) 经过数据预处理后的数据记录Fig.9 (a) Raw record for 21th shot with picked traveltimes for first-arrival P waves (red dashed line) and Rayleigh waves (blue dashed line); (b) Data after pre-processing

4.2 反演结果

通过对瑞雷面波频散曲线进行反演(Zhang et al., 2015)获得的S波速度可以作为联合反演的初始S波速度模型，如图10b所示，该初始S波速度模型被离散为30×121等体积立方体网格，网格间距为2.5 m.从图可知，在30 m深度范围内，从左到右，S波速度从420 m·s-1递增到530 m·s-1，低速异常体位于水平方向100～150 m，这意味着断层地表水平位置可能位于150～170 m；深层为一高速带，故在45 m以下的区域设置为650 m·s-1常速度.基于此S波速度模型，以及从图9a估算的P波速度值(2900 m·s-1)，我们可以构建初始P波速度模型，如图10a所示.

图11a是经过15次迭代后单独反演P波速度结果，图11b是经过15次迭代后交叉梯度联合反演P波速度结果.由图可知，相比于单独反演，交叉梯度联合反演P波速度结果并没有得到提高.然而与初始P波速度相比，反演结果确有很大提高，其中低速异常体面积扩大，从中可以推断隐伏断层水平位置可能位于230～280 m，这与共偏移距结果指示的隐伏断层位置更加吻合.

图12所示为经过15次迭代反演S波速度结果.图12a为单独反演S波速度结果，可见在水平位置100～200 m处仍然存在一低速异常体，但是该异常体的形态与P波反演结果形态略有不同.并且在浅部水平位置250～300 m处存在一高速异常体，这与P波反演结果不同.图12b为交叉梯度联合反演S波速度结果，该结果中低速异常体的位置、形态与P波速度反演结果非常相似，而且浅部也未见局部高速异常体.单独反演中，S波速度反演结果与P波速度反演结果相似度不高；而在交叉梯度联合反演中，S波速度与P波速度反演结果相似度极高，其反演结果更真实可靠.

5 结论与讨论

本文提出了一种初至P波和瑞雷面波联合反演的方法，对初至P波进行全波形反演，以及对瑞雷面波采用加窗振幅波形反演，同时将P波速度和S波速度的交叉梯度作为二者反演的正则化约束项.数值模拟结果表明，与单独反演相比，联合反演可以消除S波反演结果中的伪异常，提高S波反演精度；对于P波速度，联合反演并不能获得更好的反演结果.实际资料反演结果表明，交叉梯度联合反演的S波速度与P波速度反演结果相似度更高，其反演结果更可信.

交叉梯度联合反演的缺点是，当真实的P波速度模型与S波速度模型在结构上相似度不高时，采用交叉梯度作为反演约束项会得到错误的反演结果.

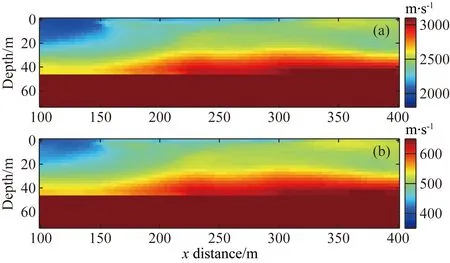
图10 初始速度模型(a) 基于初始S波速度模型估算出的初始P波速度模型； (b) 通过面波频散曲线反演获得的S波速度作为初始S波速度.Fig.10 Initial velocity models(a) Initial P-wave velocity model estimated based on initial S-wave velocity model; (b) Initial S-wave velocity model computed from surface-wave dispersion inversion.

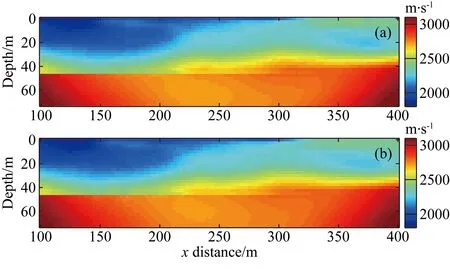
图11 初至P波波动方程走时反演结果(a) 单独反演第15次迭代P波速度结果； (b) 联合反演第15次迭代P波速度结果.Fig.11 Inversion results for first-arrival P waves(a) Single inversion of P-wave velocity after 15 iterations; (b) Joint inversion of P-wave velocity after 15 iterations.

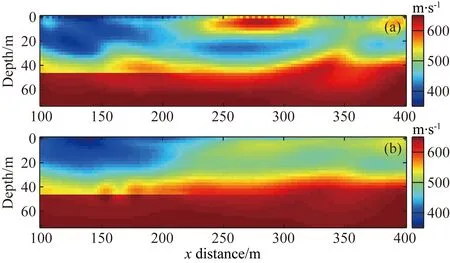
图12 S波波动方程走时反演结果(a) 单独反演第15次迭代S波速度结果； (b) 联合反演第15次迭代S波速度结果.Fig.12 Inversion results for S-wave velocity(a) Single inversion of S-wave velocity after 15 iterations; (b) Joint inversion of S-wave velocity after 15 iterations.

Abma R, Kabir N. 2006. 3D interpolation of irregular data with a POCS algorithm.Geophysics, 71(6): E91-E97.

Castagna J P, Batzle M L, Eastwood R L. 1985. Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks.Geophysics, 50(4): 571-581. Colombo D, De Stefano M. 2007. Geophysical modeling via simultaneous joint inversion of seismic, gravity, and electromagnetic data: Application to prestack depth imaging.TheLeadingEdge, 26(3): 326-331. Gallardo L A, Meju M A. 2003. Characterization of heterogeneous near-surface materials by joint 2D inversion of DC resistivity and seismic data.GeophysicalResearchLetters, 30(13): 1658. Hestenes M R, Stiefel E. 1952. Methods of conjugate gradients for solving linear systems.JournalofResearchoftheNationalBureauofStandards, 49(6): 409-436.

Hoversten G M, Cassassuce F, Gasperikova E, et al. 2006. Direct reservoir parameter estimation using joint inversion of marine seismic AVA and CSEM data.Geophysics, 71(3): C1-C13.

Hu J F, Duan Y K, Hu Y L, et al. 1999. Inversion of Shear-wave velocity structure in shallow soil from Rayleigh waves.ChineseJ.Geophys. (in Chinese), 42(3): 393-400.

Hu W Y, Abubakar A, Habashy T M. 2009. Joint electromagnetic and seismic inversion using structural constraints.Geophysics, 74(6): R99-R109.

Hu Z Z, Hu X Y, He Z X. 2006. Pseudo-Three-Dimensional magnetotelluric inversion using nonlinear conjugate gradients.ChineseJ.Geophys. (in Chinese), 49(4): 1226-1234.

Kowalsky M B, Finsterle S, Peterson J, et al. 2005. Estimation of field-scale soil hydraulic and dielectric parameters through joint inversion of GPR and hydrological data.WaterResourcesResearch, 41(11): W11425, doi:10.1029/2005WR004237.

Li M M, He Y M. 2011. Lithospheric structure beneath northeastern boundary region of the north China craton from Rayleigh wave dispersion inversion.ActaSeismologicaSinica(in Chinese), 33(2): 143-155.

Li Z X, Tan H D, Fu S S, et al. 2015. Two-dimensional synchronous inversion of TDIP with cross-gradient constraint.ChineseJ.Geophys. (in Chinese), 58(12): 4718-4726, doi: 10.6038/cjg20151232.

Liu Y K, Chang X, Wang H, et al. 2001. Estimation of near-surface velocity and seismic tomographic static corrections.ChineseJ.Geophys. (in Chinese), 44(2): 272-278. Luo Y, Schuster G T. 1991a. Wave equation inversion of skeletalized geophysical data.GeophysicalJournalInternational, 105(2): 289-294. Luo Y, Schuster G T. 1991b. Wave-equation traveltime inversion.Geophysics, 56(5): 645-653.

Peng M, Tan H D, Jiang M, et al. 2013. Three-dimensional joint

inversion of magnetotelluric and seismic travel time data with cross-gradient constraints.ChineseJ.Geophys. (in Chinese), 56(8): 2728-2738, doi: 10.6038/cjg20130821.

Pratt R G, Shin C, Hick G J. 1998. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion.GeophysicalJournalInternational, 133(2): 341-362.

Schäfer M, Groos L, Forbriger T, et al. 2013. 2D Full waveform inversion of recorded shallow seismic Rayleigh waves on a significantly 2D structure. ∥ Near Surface Geoscience 2013-19th EAGE European Meeting of Environmental and Engineering Geophysics. EAGE.Shi Y L, Jin W. 1995. Genetic algorithms inversion of lithospheric structure from surface wave dispersion.ChineseJ.Geophys. (ActaGeophysicaSinica) (in Chinese), 38(2): 189-198.

Solano C A P, Donno D, Chauris H. 2013. 2D surface wave inversion in the F-K domain. ∥ 75th EAGE Conference & Exhibition incorporating SPE EUROPEC. EAGE.

Solano C A P, Donno D, Chauris H. 2014. Alternative waveform inversion for surface wave analysis in 2-D media.GeophysicalJournalInternational, 198(3): 1359-1372.

Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation.Geophysics, 49(8): 1259-1266.

Virieux J, Operto S. 2009. An overview of full-waveform inversion in exploration geophysics.Geophysics, 74(6): WCC1-WCC26.

Xia J H, Miller R D, Park C B. 1999. Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves.Geophysics, 64(3): 691-700.Yu P, Dai M G, Wang J L, et al. 2009. Joint inversion of

magnetotelluric and seismic data based on random resistivity and velocity distributions.ChineseJ.Geophys. (in Chinese), 52(4): 1089-1097.Zhang Z D, Liu Y K, Schuster G. 2015. Wave equation inversion of skeletonized surface waves. ∥ 2015 SEG Annual Meeting. New Orleans, Louisiana: Society of Exploration Geophysicists.

附中文参考文献

胡家富, 段永康, 胡毅力等. 1999. 利用Rayleigh波反演浅土层的剪切波速度结构. 地球物理学报, 42(3): 393-400.

胡祖志, 胡祥云, 何展翔. 2006. 大地电磁非线性共轭梯度拟三维反演. 地球物理学报, 49(4): 1226-1234.

李明明, 何玉梅. 2011. 利用瑞雷面波反演华北克拉通东北部边界的岩石圈结构. 地震学报, 33(2): 143-155.

李兆祥, 谭捍东, 付少帅等. 2015. 基于交叉梯度约束的时间域激发极化法二维同步反演. 地球物理学报, 58(12): 4718-4726, doi: 10.6038/cjg20151232.

刘伊克, 常旭, 王辉等. 2001. 三维复杂地形近地表速度估算及地震层析静校正. 地球物理学报, 44(2): 272-278.

彭淼, 谭捍东, 姜枚等. 2013. 基于交叉梯度耦合的大地电磁与地震走时资料三维联合反演. 地球物理学报, 56(8): 2728-2738, doi: 10.6038/cjg20130821.

石耀霖, 金文. 1995. 面波频散反演地球内部构造的遗传算法. 地球物理学报, 38(2): 189-198.

于鹏, 戴明刚, 王家林等. 2009. 电阻率和速度随机分布的MT与地震联合反演. 地球物理学报, 52(4): 1089-1097.

(本文编辑 何燕)

Joint inversion of first arrival P waves and Rayleigh waves based on cross-gradient constraint

FU Lei, LIU Si-Xin

CollegeofGeo-explorationScienceandTechnology,JilinUniversity,Changchun130026,China

In seismic exploration, knowledge of the near-surface velocity can improve the construction of an accurate geological model. Until recently, most surface-wave inversion approaches assumed a layered model, which is not justified in a complex geological environment.To overcome this 1D limitation, researchers have begun to explore the benefits of 2D waveform inversion of surface waves. Windowed-Amplitude waveform inversion is a replacement to classical Full Wave form Inversion (FWI), which has faster convergence, however, lower spatial resolution in the tomogram is deduced. To partly recover this lost resolution, we propose a joint inversion of first arrival P-wave data and Rayleigh wave data that uses the cross-product between the P-velocity and S-velocity gradients as a regularization term. First, the P-velocity model is inverted by the full waveform inversion method, in which the first arrivals are those of the refraction and direct arrivals. Then, the amplitude spectra of the surface waves in the frequency-wavenumber domain are inverted for the S-velocity model with a cross-product constraint. This constraint regularization insists that the S-velocity gradient is closely parallel to that of the P-velocity gradient. Results show that cross-product regularization provides a significant reduction in artifacts in the S-velocity tomogram. In this case the less robust inversion of surface waves is combined with high resolution P-wave tomography to achieve better spatial resolution of the S-wave velocity tomogram.

First-arrival P wave; Rayleigh wave; Cross-gradient; Joint inversion

10.6038/cjg20161209.

国家自然科学基金项目(3A515AV44423),中国博士后科学基金(801151010423)共同资助.

傅磊，男，1985年生，讲师，主要从事地球物理正反演及成像研究.E-mail: leifu@jlu.edu.cn

10.6038/cjg20161209

P631

2016-02-01，2016-11-14收修定稿

傅磊，刘四新. 2016. 基于交叉梯度约束的地震初至纵波与瑞雷面波联合反演. 地球物理学报，59(12):4464-4472,

Fu L, Liu S X. 2016. Joint inversion of first arrival P waves and Rayleigh waves based on cross-gradient constraint.ChineseJ.Geophys. (in Chinese),59(12):4464-4472,doi:10.6038/cjg20161209.