医学论文中“相关性分析”和“关联性分析”的正确使用
官 鑫,王 丽,姜瑾秋,李欣欣,韩宏志
(《吉林大学学报(医学版)》编辑部,长春130021)
相关性分析及关联性分析是医学研究中描述事件间联系性质和程度的常用方法。从哲学层面讲,任何事物的存在都并非孤立,既相互联系又相互制约的。蔡智澄等[1]认为:在社会生活中存在的所有关系均可以归结为两种关系,即具有唯一性的一一对应关系(函数关系)和非唯一性的统计关系(关联关系)。人们通常采用相关性分析法和关联性分析法来揭示、分析、解释这种关系的密切程度。
医学论文的题目和内容中常会出现“……相关性分析”或“……关联性分析”,有些作者或编辑并没有意识到“相关性”与“关联性”有何区别,但这两者所表达的意义确有不同。
1 “相关性分析”的概念及基本特征
“相关性”是一个统计学名词,《卫生统计学》[2]教科书中将“相关”定义为随机变量之间相互联系的密切程度和方向。“相关性分析”是对自然界和社会中的两种或多种事物(或现象)是否相关,测度事物(或现象)间统计关系强弱(或变量之间线性相关程度强弱),反映事物(或数据)之间的趋同关系的一种常用的手段和工具。
常用的相关系数是由英国统计学家卡尔·皮尔逊提出的简单相关系数。其数学表达式为
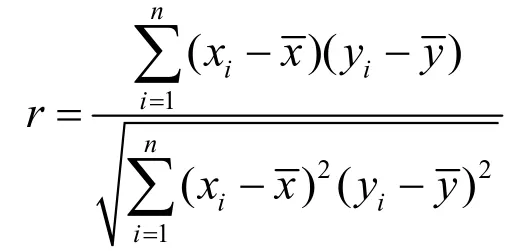
x和y为两个待研究变量,(xi,yi) (i=1,2,…,n)为两变量的n对观察值,x和y分别为n个观察值的均值。杜秀杰等[3]研究显示:相关系数r是一个无量纲的数值,且-1≤r≤1。|r|越接近1,说明相关性越好,|r|越接近0,说明相关性越差。
“相关性”按涉及变量的多少分为一元相关和多元相关,按表现形式分为直线相关和曲线相关,按变化方向不同分为正相关和负相关。医学论文中常用的“相关性分析”检验方法有线性相关分析法、Pearson相关分析法、Spearman相关分析法、秩相关分析法和回归分析等。值得注意的是,回归分析是相关性分析中一种特殊的形式,回归有相关关系、伴随关系和依存关系,当作为相关关系时其可以归为相关性分析的一种。直线相关系数r是用来说明直线相关的两个变量相关关系的密切程度和相关方向的统计指标,而回归系数是回归直线的斜率,是通过x推算y的回归系数,表示当x变动一个单位时,y平均变动的单位。直线相关分析中要求x和y均符合正态分布,而回归分析要求y符合正态分布。
李柏松[4]的研究显示,“相关性分析”具有如下特征:①概念具体(两变量数量协同变化关系或规律);②简单的分析变量搭配形式少,复杂的分析变量搭配形式多;③可分为静态或动态分析;④相关分析的统计量无量纲,但回归分析的统计量有量纲;⑤有相关的正负向之分;⑥回归分析区分原因和结果变量,其他相关分析不区分原因和结果变量;⑦两个变量同时参与计算分析。
2 “关联性分析”的概念及基本特征
“关联性分析”是针对两个变量或多个变量一系列对应测量值的随机样本资料,应用生物统计假设检验的方法分析和推断变量间的数量关系或数量协同变化关系是否存在,并在确定变量间存在关联性的基础上评价关联程度的一种方法[4]。
“关联性分析”中可以得出关联系数。但不可将关联系数误认为是相关系数(例如 Pearson相关系数、Spearman相关系数等),分类资料中的四格表的列联系数是多数人比较熟悉的关联系数的一种。目前医学科研统计分析中,很少看到在差异性分析基础上,同时运用关联分析的情况,表明人们对此还缺乏正确的认识。常用的关联系数有:①两独立样本的t检验或方差分析,皆可用η系数做关联性分析,;②结果变量为分类资料的关联系数;③分类资料中的四格表的列联系数;④结果变量为等级资料的关联系数计算时根据秩和检验的Z值、H值转换为2χ值,再求取v系数。在两变量的静态数量关系分析中,关联系数取值为[0,1],一般不考虑正负向。其值越接近于1,说明变量之间关联程度越高;其值越接近于0,说明变量之间关联程度越低。
因研究目的不同,关联性分析可分为较多类别:例如定量变量间关联性分析、定序或定类变量间关联性分析;线性关联性分析和非线性关联性分析;静态关联性分析与动态关联性分析;双变量关联性分析与复关联性分析;实值关联性分析与灰色关联性分析等。两变量的“关联性分析”包括线性相关、秩相关和分类变量的关联性分析,前两者属于“相关性分析”。
“关联性分析”的特征有:①概念宽泛(两变量间相互或单向影响);②变量的措配形式多;③统计量的关联系数无量纲;④多为静态分析;⑤关联不分正负向,统计量只表达关联程度;⑥一般区分原因变量和结果变量;⑦原因变量不参与计算分析。医学论文中常用的“关联性分析”检验方法有t检验、方差齐性检验、Z检验、正态性检验(W检验)、2χ检验、方差分析、多重极差检验(SNK法)、Dunnett法、Bonfferoni法、秩和检验和疾病与暴露因素的关联分析(相对危险度(RR)、归因危险度(AR)、人群归因危险度(PAR)、优势比(OR))及Meta分析等。
3 相关性分析和关联性分析的区别
从“相关性分析”和“关联性分析”的概念和特征可见其主要区别有:①概念的宽泛程度不一,“相关性分析”的概念具体,“关联性分析”的概念宽泛;②变量搭配形式不同,“相关性分析”的变量搭配形式相对较少,“关联性分析”的变量搭配形式相对较多;③分析的动静态不同,“相关性分析”有静态或动态之分,“关联性分析”多为静态分析;④关联的正负向之分,“相关性分析”有相关的正负向之分,“关联性分析”不分正负向;⑤是否区分原因和结果变量,回归分析区分原因和结果变量,其他相关分析不区分原因和结果变量,“关联性分析”一般区分原因变量和结果变量;⑥两个变量是否同时参与计算分析,“相关性分析”的两个变量同时参与计算分析,而“关联性分析”的原因变量不参与计算分析。
4 医学论文中“关联性分析”或“相关性分析”的应用示例
以“相关性分析”为主题词,不限定年限检索医药卫生文献,一次可以检索到上万条,但阅读原文发现:大部分论文中“相关性分析”方面的结果只是论文结果的一部分或一小部分内容。如果论文结果中相关性分析结果仅是论文内容的一部分,则论文的题名应采用“关联性分析”而非“相关性分析”,因为“相关性分析”不能全面准确地反映论文的主题思想和主要内容,宜使用“关联性分析”作为题目。如果论文的内容只涉及“相关性分析”的内容,而并无其他内容,则论文题目可以使用“相关性分析”。因此笔者认为:医学论文题名中究竟采用“相关性分析”还是“关联性分析”,要根据论文的具体内容来决定。
例1 王蓓蓓等[5]关于《2型糖尿病患者TSH水平与颈动脉粥样硬化的相关性分析》一文报道了亚临床甲状腺功能减退与甲状腺功能正常的2型糖尿病患者的一般资料、血压、血脂、血糖等变化结果,TSH 分层后上述各指标比较结果,血清TSH水平与颈动脉粥样硬化的相关性分析结果。
例1中相关性分析结果仅是论文内容中的小部分结果。因此建议文章题目改为《2型糖尿病患者TSH水平与颈动脉粥样硬化的关联性分析》比较合适。
例2 随机抽取15名健康成人,测定血液的凝血酶浓度及凝固时间,据此数据如何判断这两项指标间是否相关?[2]

受试者号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15凝血酶浓度/mL 1.1 1.2 1.0 0.9 1.2 1.1 0.9 0.6 1.0 0.9 1.1 0.9 1.1 1.0 0.7凝血时间/s 14 13 15 15 13 14 16 17 14 16 15 16 14 15 17
例2可由数据计算出=216.7,带入公式r=-0.926,可见两变量呈负相关关系,且|r|接近1,说明相关性非常高,凝血时间随凝血酶浓度增高而缩短,这里使用的就是相关性分析,因此在论文的内容和题目中应该使用“相关性分析”而非“关联性分析”。
例3 为观察婴儿腹泻是否与喂养方式有关,某医院儿科随机选取了消化不良的婴儿82例,观察其与喂养方式之间的关联性[2]。

喂养方式 腹泻 合计有 无人工 30 10 40母乳 17 25 42合计 47 35 82
综上所述,“相关性分析”和“关联性分析”的概念、特征、计算公式及其意义均不相同;其对资料的分布类型、变量间的关系类型和样本量的要求也均不相同,“关联性分析”对于资料的分布类型、变量间的关系类型的要求限制少于“相关性分析”,如秩和检验属于“关联性分析”,其适用范围较广,适用总体分布类型未知或非正态分布的资料,其数据一端或二端为数据不明确的资料以及有序多分类资料(如等级资料等);该方法简便、易于理解和掌握。但是对于符合参数检验条件的资料使用非参数检验会降低检验效率,因此对于原始数据应该首先分析资料的类型和变量间的关系,对于符合参数检验应的首选参数检验,或经变量变换后符合参数检验的应首先进行变量的变换,若不能满足参数检验条件,则选用非参数检验。而“相关性分析” 对于资料的分布类型、变量间的关系类型的要求限制较多,如直线相关分析要求直线相关分析中要求两变量均符合正态分布,在两变量线性数量变化关系髙度密切时,可采用线性回归分析模型拟合这种变化规律。由此可见线性回归分析是两变量撞势性的研究方法之一,该分析的模型参数估计值共有2种量纲:一为截距量纲,同应变量(结果变量);二为自变量系数(回归系数或偏回归系数)量纲,为比例量纲(分母为自变量单位量纲,分子为应变量量纲)。由于“相关性分析”要求资料应符合正态分布,因此对样本量的要求较“相关性分析”更严格。因此在医学论文的题目和内容中应注意区别使用“相关性分析”和“关联性分析”。
[1]蔡智澄,何立民.相关性分析原理在图书情报分析中的应用[J].现代情报,2006(5):151-152,156.
[2]方积乾.卫生统计学[M].5版.北京:人民卫生出版社,2005:206-220.
[3]杜秀杰,赵大良,葛赵青,等.学术论文的下载频率与被引频率的相关性分析[J].编辑学报,2009,21(6):551-553.
[4]李柏松.关联性分析在医学科研中的应用与价值[D].重庆:重庆医科大学,2015.
[5]王蓓蓓,陈新焰,张杉杉,等.2型糖尿病患者TSH 水平与颈动脉粥样硬化的相关性分析[J].中国生化药物杂志,2014,34(8):120-123.

