围护结构热湿耦合传递模型及简便求解方法

刘向伟，陈友明，陈国杰,3，郭兴国，罗娜

(1. 南昌大学 建筑工程学院，南昌 330031；2. 湖南大学 土木工程学院，长沙 410082；3. 南华大学 城市建设学院，湖南 衡阳 421001)



围护结构热湿耦合传递模型及简便求解方法

刘向伟1，陈友明2，陈国杰2,3，郭兴国1，罗娜1

(1. 南昌大学 建筑工程学院，南昌 330031；2. 湖南大学 土木工程学院，长沙 410082；3. 南华大学 城市建设学院，湖南 衡阳 421001)

为了预测围护结构内的温度和湿度分布，以连续变量,相对湿度和温度为驱动势，考虑热传递与湿传递之间的耦合作用，建立了围护结构热湿耦合传递非稳态模型，并提出了基于多物理场耦合仿真模拟软件COMSOL的热湿耦合传递模型简便求解方法。通过对比新建模型模拟结果与HAMSTAD标准验证实例，验证了模型及求解方法的准确性。

围护结构；热湿耦合传递；相对湿度；含湿量

围护结构多由多孔介质材料构建而成，其内热传递与湿传递属于典型的多孔介质热质传递过程。1957年Philip等[1]首次提出以温度和含湿量为驱动势，考虑多孔介质材料内热传递、湿迁移及其耦合作用,建立了多孔介质材料热湿耦合传递模型。在Philip研究的基础上，Pedersen[2]，Liesen等[3]，Lu[4]，Belarbi等[5]，Zhong[6]，郭兴国等[7]，Chu等[8]，孔凡红等[9-10]，Qin等[11]，Leskovsek等[12]，Liu等[13]和Vasilyev等[14]分别建立了多孔介质材料的热湿耦合传递模型。尽管对围护结构内的热湿传递现象进行了大量研究，但由于围护结构热湿耦合传递模型为变系数偏微分方程组，高度非线性且相互耦合，如何简便求解围护结构热湿耦合传递模型仍是围护结构热湿耦合研究领域的一大难题。

目前,求解围护结构热湿耦合传递模型常用的方法是先将控制方程和边界条件用有限差分法[15]、有限容积法[16]或有限元法[17]进行离散，将偏微分方程组转化为代数方程组，然后设计算法，编程求解离散后得到的代数方程组，从而得到温度和湿度在离散点处的值。由于热湿耦合传递模型的离散过程繁琐、复杂，需深厚的数学基础，而程序算法设计需熟练掌握某种程序设计语言，且模型修改后需重新对其进行离散，这在很大程度上使研究仅停留在理论层面，难以应用于工程实际。

首先建立围护结构热湿耦合传递数学模型，然后提出围护结构热湿耦合传递模型简便求解方法，最后通过对比模型模拟结果与HAMSTAD验证实例，验证模型及简便求解方法的准确性。

1 围护结构热湿耦合传递模型

1.1 控制方程

为了避免驱动势在交界面处不连续，采用连续变量，温度和相对湿度，作为驱动势，根据单元体质量和能量守恒建立建筑围护结构热湿耦合传递非稳态模型。

1.1.1 湿控制方程 虽然围护结构内气液两相湿流动不能严格的区分开来，但计算围护结构内湿流动的一个有效方法是将湿流量分为水蒸气扩散和液态水迁移两部分来计算。根据单元体质量守恒，得

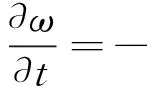
(1)

式中:ω为含湿量，kg/m3；t为时间，s；jv为水蒸气扩散速率，kg/(m2·s)；jl为液态水传递速率，kg/(m2·s)。

根据菲克定律,得

jv=-δp▽Pv

(2)

式中:δp为水蒸气渗透率，kg/(m·s·Pa)；Pv为水蒸气分压力，Pa。

根据达西定律，得

jl=Kl▽Pk

(3)

式中:Kl为液态水渗透率，kg/(m·s·Pa)；Pk为毛细水压力，Pa。

将式(2)、(3)代入式(1)，得

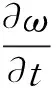
(4)

体积含湿量是温度和相对湿度的函数，即

ω=f(φ,T)

(5)

式中:T为温度，K；φ为相对湿度。

将方程(5)两边同时对时间t求偏导，得

(6)

忽略温度对材料平衡含湿量的影响，则方程(6)可以简化为

(7)

式中:ζ为湿容(等温吸放曲线的斜率)，kg/m3。

多孔介质材料孔隙内混合气体(湿空气)按理想气体处理，则

Pv=φPs

(8)

式中:Ps为饱和蒸汽压力，Pa。

式(8)两边同时求导，得

▽Pv=Ps▽φ+φ▽Ps

(9)

由于饱和水蒸汽压力Ps为温度的单值函数

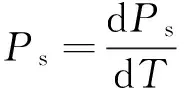
(10)

将式(10)代入式(9)得

(11)

根据开尔文关系式，得

Pk=-ρlRDTln(φ)

(12)

式中:ρl为液态水的密度，kg/m3；RD为水蒸气气体常数，J(kg·K)。

方程(12)两边同时求导，得

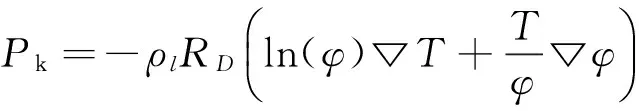
(13)

将式(7)、(11)和(13)代入式(4)，得

(14)

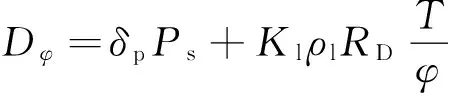
1.1.2 热控制方程 根据单元体能量守恒，控制单元内焓的变化等于流入控制单元的净能量。能量守恒方程可表示为

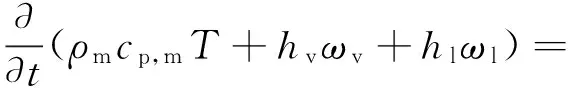
(15)

式中:ρm为干材料密度，kg/m3；cp,m为干材料的比热，J/(kg·K)；ωv为水蒸气形式的含湿量，kg/m3；ωl为液态水形式的含湿量，kg/m3；hv为水蒸气的比焓，J/kg；hl为液态水的比焓，J/kg；qc为热流密度，W/m2。

水蒸气的比焓可以表示为液态水的比焓与汽化潜热之和。

hv=hl+hlv

(16)

式中:hlv为水蒸气的汽化潜热，J/kg。

假设水蒸气汽化潜热、干材料和液态水的比热为常数，将式(16)代入式(15)，整理得

(17)

式中:cp,l为液态水的比热，J/(kg·K)。

与水蒸气汽化潜热相比，水蒸气和液态水的显热可以忽略不计，故式(17)右边第二项可以忽略。尽管水蒸气的汽化潜热很大，但由于水蒸汽传递速率小，水蒸气形式的含湿量变化率非常小，式(17)右边第三项也可以忽略不计，式(17)可简化为

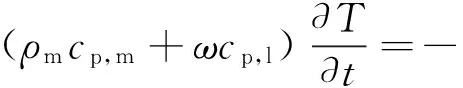
(18)

根据傅里叶定律，得

qc=-k▽T

(19)

式中:k为导热系数，W/(m·K)。

将式(19)代入式(18)，得

(20)

1.2 边界条件

通过围护结构外表面的湿流量gn,e可表示为：

gn,e=βp,e(φePs,e-φsurfePs,surfe)

(21)

式中:βp,e为围护结构外表面对流传质系数，kg/(m2·s·Pa)；φe为室外相对湿度；φsurfe为围护结构外表面相对湿度；ps,e为室外饱和水蒸汽压力，Pa；ps,surfe为围护结构外表面饱和水蒸汽压力，Pa。

通过围护结构外表面的热流量qn,e包括对流换热，太阳辐射及水蒸气潜热。

qn,e=he(Te-Tsurfe)+hlvgn,e+αqsolar

(22)

式中:he为外表面对流换热系数，W/(m2·K)；Te为室外空气温度，K；Tsurfe为围护结构外表面温度，K；α为围护结构外表面太阳辐射吸收率；qsolar为垂直照射在围护结构外表面上的太阳辐射，W/m2。

通过围护结构内表面的湿流量gn,i可表示为

gn,i=βp,i(φiPs,i-φsurfiPs,surfi)

(23)

式中:βp,i为围护结构内表面对流传质系数，kg/(m2·s·Pa)；φi为室内相对湿度；φsurfi为围护结构内表面相对湿度；ps,i为室内饱和水蒸汽压力，Pa；ps,surfi为围护结构内表面饱和水蒸汽压力，Pa。

通过围护结构内表面的热流量qn,i可表示为

qn,i=hi(Ti-Tsurfi)+hlvgn,i

(24)

式中:hi为内表面对流换热系数，W/(m2·K)；Ti为室内空气温度，K；Tsurfi为围护结构内表面温度，K。

2 围护结构热湿模型简便求解方法

围护结构热湿耦合传递模型为变系数偏微分方程组，高度非线性且相互耦合，为了获得围护结构内的温湿度分布，控制方程需同时求解。为了避免传统求解方法中繁琐、复杂的手动离散过程以及求解算法设计，本文采用多物理场耦合仿真模拟软件COMSOL来求解围护结构热湿耦合传递模型。

COMSOL为工程或数学问题提供了偏微分方程模型(PDEs)，其控制方程和边界条件为

(25)

式中:u为因变量;ea为质量系数;da为衰减系数;c为扩散系数;α为守恒通量对流系数;γ为守恒通量源;β为对流系数;a为吸收系数;f为源项;n为朝外的单位向量;g为边界通量/源;q为边界吸收/阻抗项。

围护结构热湿耦合传递模型中因变量T和φ写成矩阵形式u=(T,φ)，则控制方程在COMSOL的偏微分方程模块中可表示为

(26)

其中:C=ρmcp,m+ω cp,l

外表面边界条件可表示为

(27)

内表面边界条件可表示为

(28)

COMSOL用有限元方法自动对模型进行离散，并用数值求解器求解离散后的代数方程组，避免了繁琐、复杂的手动离散过程以及求解算法设计，研究者和用户能方便地对已有的模型进行修改或二次开发。在网格划分方面COMSOL自带预定义的三角形网格单元划分方式，用户只需选择合理的网格尺寸(极端粗化、特别粗化、较粗化、粗化、正常、细化、较细化、特别细化、极端细化)对研究对象进行网格划分。网格尺寸越密，计算越精确，但所需计算时间越长。对于围护结构热湿耦合传递研究而言，正常的网格尺寸是合理的网格尺寸，但分析雨水吸收问题时，为了计算收敛，需要选取特别细化的网格尺寸。COMSOL求解流程图如图1所示。

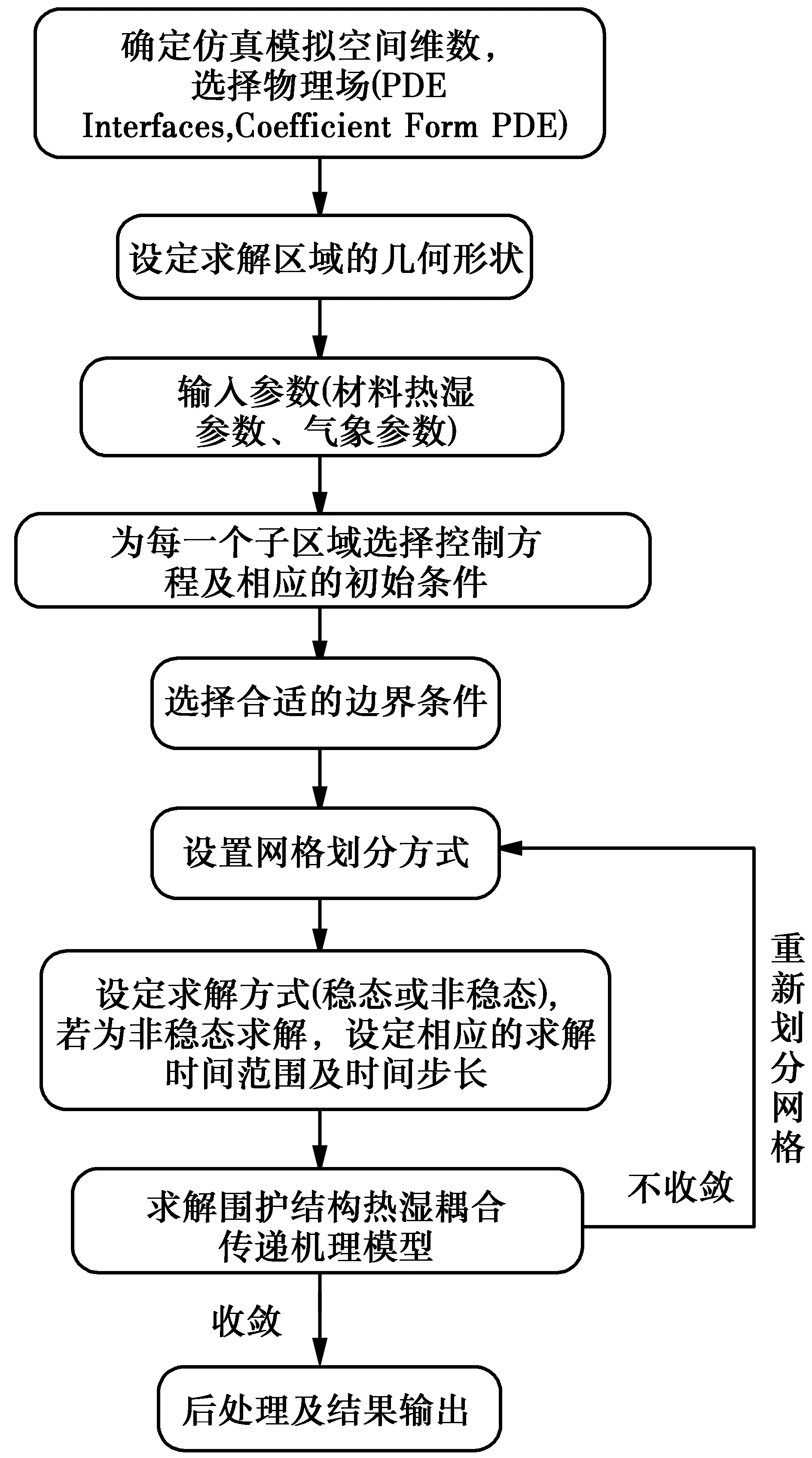
图1 COMSOL求解流程图

3 热湿耦合模型及求解方法验证

围护结构热湿耦合模型是对实际物理现象和过程的抽象与简化，模型高度非线性且相互耦合，数值求解过程中难免会有误差，因而在模型应用前需对其进行验证。本文通过对比新模型模拟结果与HAMSTAD验证实例来验证模型及求解方法。

3.1 HAMSTAD验证实例2

HAMSTAD验证实例2分析了200 mm厚的单层各向同性墙体的等温干燥过程。初始条件为20 ℃，95%。在开始时刻，周围环境的相对湿度突然改变，室外相对湿度变为45%，室内相对湿度变为65%，室内外对流换热系数均为25 W/(m2·K)，室内外对流质传递系数均为1×10-3s/m 。材料热湿参数见表1。验证实例的详细描述见文献[18]。100、300、1 000 h时，墙体内的含湿量分布如图2所示。从对比结果可以看出，新建模型模拟结果与HAMSTAD验证实例2中的分析解吻合良好。

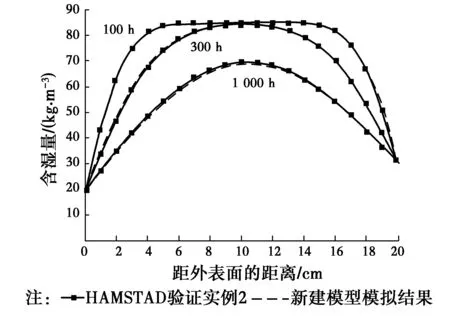
图2 100、300、1 000 h时墙体内的含湿量分布

表1 各向同性墙体的材料参数[18]

3.2 HAMSTAD验证实例5

HAMSTAD验证实例5分析了3层复合墙体内含湿量的变化。墙体构造为365 mm砖墙，15 mm砂浆层，40 mm保温层(由外至内)，初始条件为25 ℃、60%，室外温湿度为0 ℃、80%，室内温湿度为20 ℃、60%，室内外对流换热系数分别为8 W/(m2·K)和25 W/(m2·K)，室内外对流质传递系数分别为5.882 3×10-8s/m和1.838 2×10-7s/m。材料的密度、比热和导热系数见表2。材料的其他热物性参数及验证实例的详细描述见文献[18]。从图3可以看出，新建模型模拟结果与HAMSTAD验证实例5中的结果吻合良好。

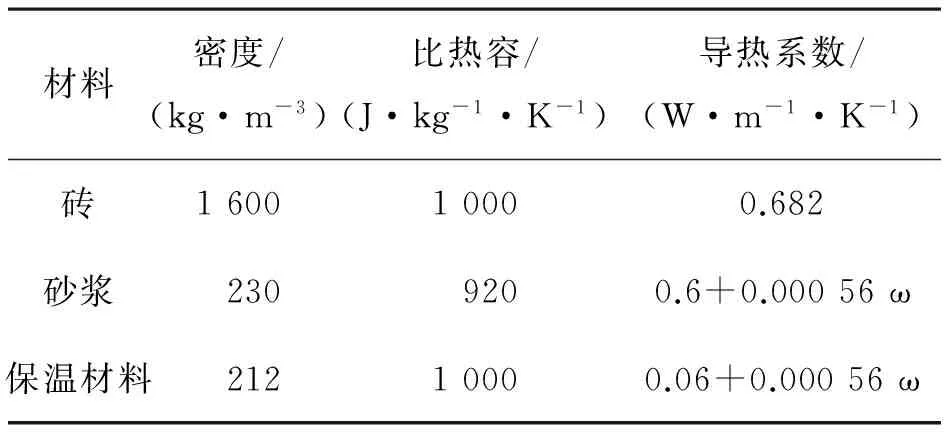
表2 墙体部件的密度、比热容和导热系数[18]

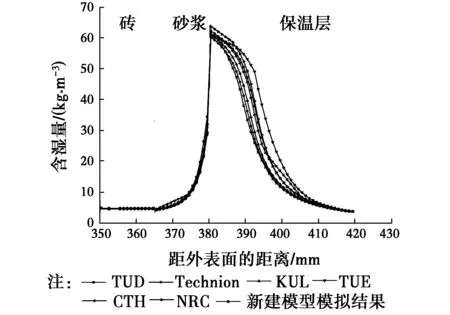
图3 60 d后墙体内的含湿量分布(TUD, Technion, KUL, TUE, CTH和NRC表示参与HAMSTAD项目的其他研究机构的模拟结果)

4 结 论

本文以多孔介质材料传热传质理论为基础，根据单元体质量和能量守恒，建立了围护结构热湿耦合传递非稳态模型，并提出了基于多物理场耦合仿真模拟软件COMSOL的热湿耦合传递模型简便求解方法。通过对比新建模型模拟结果与HAMSTAD验证实例2和5，验证了模型及求解方法的准确性。该模型可为优化围护结构热工性能，预测围护结构湿损坏提供理论依据和技术指导。

[1] PHILIP J R，DEVRIES D A．Moisture movement in porous materials under temperature gradients [J]．Transactions American Geophysical Union，1957，38(2)：222-232．

[2] PEDERSEN C R．Combined heat and moisture transfer in building constructions [D]．Copenhagen：Technical University of Denmark，1990：24-56．

[3] LIESEN R，PEDERSEN C．Modelling the energy effects of combined heat and mass transfer in building elements: Part I—Theory [J]．ASHRAE Transactions，1999，105(1)：941-953．

[4] LU X．Modelling of heat and moisture transfer in buildings I. model program [J]．Energy and Buildings，2002，34(10)：1033-1043．

[5] BELARBI R，QIN M H，ABDELKARIM A M，et al．Experimental and theoretical investigation of non-isothermal transfer in hygroscopic building materials [J]．Building and Environment，2008，43(12)：2154-2162．

[6] ZHONG Z P．Combined heat and moisture transport modeling for residential buildings [D]．Indiana：Purdue University，2008：18-24．

[7] 郭兴国，陈友明，邓永强．Budaiwi模型的修正及实验验证[J]．土木建筑与环境工程，2010，32(2)；91-95．

GUO X G，CHEN Y M，DENG Y Q．A modified buidaiwi model and its experimental evaluation[J]．Journal of Civil，Architectural and Environmental Engineering，2010，32(2)：91-95．(in Chinese)

[8] CHU S S，FANG T H，CHANG W J．Modelling of coupled heat and moisture transfer in porous construction materials [J]．Mathematical and Computer Modelling, 2009，50(7/8)：1195-1204．

[9] 孔凡红．多层多孔介质层间界面处的热质耦合传递[J]．太阳能学报，2010，31(10)：1281-1286．

KONG F H．Coupled transfer of heat and mass at interface of multilayer porous media[J]，2010，31(10)：1281-1286．(in Chinese)

[10] KONG F H，ZHANG Q L．Effect of heat and mass coupled transfer combined with freezing process on building exterior envelope [J]．Energy and Buildings，2013，62：486-495．

[11] QIN M H，ABDELKARIM A M，BELARBI R．Two-dimensional hygrothermal transfer in porous building materials [J]．Applied Thermal Engineering，2010，30(16)：2555-2562．

[12] LESKOVSEK U，MEDVED S．Heat and moisture transfer in fibrous thermal insulation with tight boundaries and a dynamical boundary temperature [J]．International Journal of Heat and Mass Transfer， 2011，54(19/20)：4333-4340．

[13] LIU Y F，WANG Y Y，WANG D J，et al．Effect of moisture transfer on internal surface temperature [J]．Energy and Buildings，2013，60：83-91．

[14] VASILYEV G P，LICHMAN V A，PESKOV N V，et al．Simulation of heat and moisture transfer in a multiplex structure [J]．Energy and Buildings，2015，86：803-807．

[15] KALIS H．Efficient finite-difference scheme for solving some heat transfer problems with convection in multilayer media [J]．International Journal of Heat and Mass Transfer，2000，43(24)：4467-4474．

[16] 张景欣，郭兴国，陈友明,等．墙体内热湿耦合过程的时域递归展开算法[J]．土木建筑与环境工程，2015，37(6)；147-152．

ZHANG J X，GUO X G，CHEN Y M，et al．A time domain recursive algorithm for solving the model of coupled heat and moisture transfer model in building wall[J]．Journal of Civil，Architectural and Environmental Engineering，2015，37(6)：147-152． (in Chinese)

[17] KHOSHBAKHT M，LIN M，FEICKERT C．A finite element model for hygrothermal analysis of masonry walls with FRP reinforcement [J]．Finite Elements in Analysis and Design，2009，45(8/9)：511-518．

[18] HAGENTOFT C E．HAMSTAD-Final report：Methodology of HAM-modeling，Report R-02:8 [R]．Gothenburg：Department of Building Physics，Chalmers University of Technology，2002：5-51．

(编辑 胡玲)

Coupled heat and moisture transfer model and simple solution method for building envelopes

Liu Xiangwei1, Chen Youming2, Chen Guojie2,3, Guo Xingguo1, Luo Na1

(1. School of Civil Engineering and Architecture, Nanchang University, Nanchang 330031, P.R. China; 2. College of Civil Engineering, Hunan University, Changsha 410082, P.R. China; 3. College of City Construction, University of South China, Hengyang 421001,Hunan, P.R. China)

A coupled heat and moisture transfer model which takes the coupled effect between heat transfer and moisture transfer into consideration is developed to model the temperature and humidity distribution within building envelopes. The continuous variables, relative humidity and temperature are chosen as the driving potentials. And a simple solution method based on a multi-physics simulation soft, COMSOL, is proposed to solve the coupled heat and moisture transfer model simply. The numerical results of this model agree well with HAMSTAD benchmarks which are international accepted.

building envelope; coupled heat and moisture transfer; relative humidity; moisture content

2016-04-12

国家自然科学基金 (51208247、51408294)

刘向伟(1987-)，男，博士，主要从事建筑节能及围护结构热湿耦合传递研究，(E-mail)xiangwei.liu@ncu.edu.cn。

郭兴国(通信作者)，男，副教授，(Email)guoxingguo@ncu.edu.cn。

Foundation item：Natural Science Foundation of China (No.51208247, No.51408294)

TU111.4

A

1674-4764(2016)04-0007-06

10.11835/j.issn.1674-4764.2016.04.002

Received:2016-04-12

Author brief：Liu Xiangwei (1987-), PhD, main research interests: building efficiency and coupled heat and moisture transfer in building envelopes, (E-mail)xiangwei.liu@ncu.edu.cn.

Guo Xingguo(corresponding author), associate professor, (E-mail)guoxingguo@ncu.edu.cn.