供应中断下双源采购的供应链契约设计
李新军刘兴华
1(烟台大学,烟台 264005)2(大连理工大学,大连 116024)
供应中断下双源采购的供应链契约设计
李新军1,2刘兴华1
1(烟台大学,烟台 264005)2(大连理工大学,大连 116024)
考虑由一个制造商和两个供应商构成的两级供应链契约设计问题,将可靠性服从随机分布的供应商作为主供应商,将完全中断供应商作为次供应商,建立以利润最大化为目标的签约和执行两阶段博弈的动态规划模型,得到制造商的最优契约设计。制造商根据产品零售价格的变化灵活做出只与一个供应商签约、与两个供应商同时签约或都不签约的决定,供应商根据契约设计内容决定自己的最优生产规模。研究表明:供应商最优生产规模与产品的单位生产成本呈负相关,与单位变动支付和单位惩罚成本呈正相关;次供应商的订货量与其本身的可靠性呈正相关,与主供应商的可靠性呈负相关;供应商的固定支付与其相应的可靠性呈负相关。
供应中断 契约设计 双源采购 可靠性 两级供应链
引 言
随着经济的全球化发展,企业规模的不断扩大,企业为降低成本,提升市场竞争力,将大量业务外包,只保留核心技术,加之市场竞争环境更加复杂,不确定性因素更多,承受风险更大,使得供应链表现出极度的脆弱性。而大部分制造型企业将一半以上的财力用于采购原材料,一旦供应过程遭受中断,影响企业的正常生产,势必会给企业带来极大的损失。造成中断的因素如:火灾、地震、洪涝、罢工等。因此,研究供应链的稳健性,保持企业生产的正常运作,就显得尤为重要。
关于供应商可靠性不确定的两级供应链契约设计问题,不少学者做了相关研究。Yang和Aydin等[1-3]将供应商的可靠性分为高和低两种类型,分析了可靠性信息不对称情况下供应链的契约设计问题,并指出信息价值由信息租金和渠道价值两部分组成。Sammi Y.Tang和Haresh Gurnani(2013)[4]分析了供应商可靠性随着购买商提供的激励机制而改变,将可靠性作为内生变量来考虑,且需求服从随机分布的情况下制造商的单源和双源采购策略。Wang等(2010)[5]也研究了供应商可靠性作为内生变量的情况。Krause等[6-8]使用甄别机制[9]对供应商可靠性进行分类,并通过实证分析指出改善供应商可靠性的有效机制。Ying-Ju Chen(2013)[10]研究了供应商可靠性为私人信息,购买商和供应商分别拥有后补产品两种情况下的采购契约设计。Tao Li等(2013)[11]研究了供应商的可靠性对制造商采购策略的影响,指出供应商为获取更大的订单需要努力提高自己的可靠性水平。黄松等(2014)[12]运用委托——代理理论,研究了需求不确定、制造商生产成本发生扰动的非对称信息下供应链的最优契约设计。王先甲等(2015)[13],Esmaeili等(2010)[14],王新辉等(2013)[15]等也研究了由成本因素导致的不可靠供应问题。郑志欣等(2013)[16]应用收益共享契约与奖励惩罚契约分析了在合作、非合作及混合3种竞争博弈下供应链的协调问题。Babich和Burnetas等(2007)[17]引入斯坦克尔博格模型分析了供应商存在违约风险的情况下购买商的采购契约设计。
双源选择作为缓解风险的一种工具,被越来越多的研究者所使用。Yang和Aydin等(2011)[2]将双源采购分为竞争战略和多元化战略,并分析了两种战略的优劣。Babich等(2012)[18],Tomlin(2006)[19],Tomlin 和 Wang (2005)[20],Data(2007)[21]等也研究了多元化战略对缓解风险的作用。有意思的一种模式是,Qinghua Li和Bo Li等(2015)[22]研究了零售商存在风险厌恶且信息非对称和制造商参与零售市场的双渠道供货策略,属于一个制造商向两个零售商供货的特殊情况。Chaturvedi和Martínez-de-Albéniz(2011)[23]研究了供应商的成本和供应风险为非对称信息时的多源采购问题,主要侧重于刻画目标函数的形式。Gümüs等(2011)[24]研究了两个供应商只有一个存在供应风险的情况下的竞争策略,且供应能力为其私人信息,通过已有供应状况加以表现。
现有文献大部分都只研究供应完全中断的情况,而对部分中断却鲜有涉及。本文以一个制造商和两个供应商构成的两级供应链为研究对象,在Yang和Aydin等(2011)[2]提出的不可靠供应链契约设计的基础上,引入部分中断和完全中断两种类型的供应商,将部分中断供应商作为主供应商,完全中断供应商作为次供应商;另外,Yang和Aydin等(2011)[2]的研究只考虑了惩罚成本,本文同时考虑变动支付和惩罚成本,Yang和Aydin等(2011)[2]的研究只是变动支付为0时的一种特殊情况。据此,制定出供应商的最优生产规模和制造商的最优契约设计模型。
1 模型参数与基本假设
本文考虑由一个制造商和两个不可靠供应商构成的两级供应链契约设计问题。其中,供应商包括一个部分中断供应商和一个完全中断供应商,完全中断是指一旦中断发生,供应商交货量为0;而部分中断则指中断比例随机发生,完全中断只是部分中断的一种特殊情况。由于制造商大多是风险厌恶的,本文将部分中断供应商作为主供应商,完全中断供应商作为次供应商来考虑。制造商向供应商提供一组契约,供应商根据自己的可靠性水平及契约内容决定最优生产规模,供应链契约设计及执行过程如图1所示。
对于上述双阶段决策过程,需建立相应的动态规划模型,先从执行阶段开始分析,然后再分析签约阶段,这将在第2小节进行。
1.1 模型参数
本模型主要涉及参数如下:
ρi:供应商i的可靠性水平,为供应商交付量占其生产规模的比例,i=1,2。且ρ1服从连续的随机分布,其概率密度函数为f1(x),累积分布函数为F1(x),0≤ρ1≤1,其中,ρ1=0表示供应完全中断,ρ1=1表示供应完全可靠;。表示供应商i的平均可靠性水平,反映供应商长期总的可靠性状况,:供应商i的初始单位生产成本,由于供应中断的存在,供应商的实际单位生产成本为(高可靠性供应商的实际单位生产成本小于低可靠性供应商的实际单位生产成本),其中,第一个供应商的实际单位生产成本为,第二个供应商的实际单位生产成本为。K:制造商的交易费用,此成本对两个供应商无差异。r:产品的零售价格。D:产品的市场需求量。zi:供应商i的生产规模。(Xi,qi,pi,vi):制造商提供给供应商 i的契约,Xi:制造商给供应商i的固定支付,qi:制造商给供应商i的订货量,pi:制造商给供应商i的单位缺货惩罚,vi:制造商给供应商i的单位变动支付。
1.2 基本假设
模型描述做出如下假设:
(1)市场需求在制造商订货前可知,为一常量;(2)由于制造商只是对所购零件进行组装,制造商的生产成本忽略不计;(3)当供应商交付量不能满足订货量时,将付出惩罚成本;(4)两个供应商相互独立,且不考虑供应商供货提前期;(5)供应商交付原材料剩余及制造商销售产品剩余的残值均为0;(6)制造商优先考虑部分中断供应商,只有当从部分中断供应商处不能取得正的利润时,才考虑是否把完全中断供应商作为唯一供应商。
2 模型构建
假定制造商和供应商都以利润最大化为目标。下面用逆序解法先从供应商执行阶段开始分析,然后再分析签约阶段。
2.1 供应商生产决策
为了简化符号,本小节不在用下标i表示供应商i。在执行阶段,制造商给定契约(X,q,p,v),供应商选择生产规模z来最大化其期望利润。由于供应中断的存在,最终交付量为min(q,ρz),其中q表示订货量,并接受变动支付vmin(q,ρz)及惩罚成本pE(q-ρz)+。(符号 “+”定义为:当x>0时,x+=x;当x≤0时,x+=0。)供应商利润函数为:

供应商完全可靠时,供应商利润为πs(X,q,p,v)=X-cz+vz,为保证制造商给供应商的固定支付X≥0,变动支付v应满足v≤c。下面对部分中断和完全中断两种不可靠供应商进行讨论。
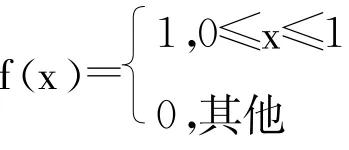
(1)对于部分中断的不可靠供应商,供应商的可靠性水平ρ服从连续的随机分布,其概率密度函数为f(x),0≤x≤1。部分中断供应商最优利润函数转化为:

供应商需决定最优生产规模z以使其利润达到最大化。定理1给出了部分中断供应商的最优生产规模及最优利润。
定理1:给定契约(X,q,p,v),对于部分中断的供应商,其最优生产规模z*(q,p,v)和最优利润如表1所示。

表1 完全中断供应商最优生产规模及最优利润
注意:z*只与q、p、v有关,而与X无关,故用z*(q,p,v)表示供应商的最优生产规模。假定,否则供应商将不进行生产,而宁愿失去变动支付,接受惩罚。
由定理1可知,由于0≤ρ≤1,因此z*≥q。当ρ=1,即供应商完全可靠时,z*=q,供应商生产规模应等于订货量;当ρ<1,即供应商不完全可靠时,z*>q,供应商生产规模应大于订货量。并且可靠性越高,即¯ρ越大,生产量越接近订货量,相同订货量对应的利润也就越大。
分析定理1,可得推论1。
推论1:供应商最优生产规模与产品的单位生产成本呈负相关,与单位变动支付和单位惩罚成本呈正相关。
理论意义:如果单位生产成本很大,供应商就会生产比较少的产品以免交货时过剩造成不必要的浪费;而如果单位变动支付和单位惩罚成本很大,供应商就会生产更多的产品以防发生供应中断造成缺货损失。

注意:z*只与q、p、v有关,而与X无关,用z*(q,p,v)表示供应商的最优生产规模。考察利润函数中z的系数,得出定理2。
定理2:给定契约(X,q,p,v),对于完全中断供应商,其最优生产规模z*(q,p,v)和最优利润如表2所示。

表2 完全中断供应商最优生产规模及最优利润
由定理2可知,供应商的最优利润与其平均可靠性水平正相关,平均可靠性越高,则供应商获得的利润越大。所以,供应商为了获取更高的利润,或得到更多的订单,必须不断努力提高自己的可靠性水平。
2.2 制造商契约设计
制造商利润由收益和成本两大部分组成,其收益包括销售商品所获得的收入和供应商交付量不能满足订货时的罚金;成本包括给供应商的固定支付、变动支付及交易费用。制造商同时向两个供应商订货,其中第一个供应商为部分中断供应商,作为主供应商;第二个供应商为完全中断供应商,作为次供应商。令,制造商的最优利润函数模型为:

约束条件:

因为制造商追求自身利润最大化,而供应商的决策变量即生产规模与固定支付无关,所以制造商总可以改变固定支付而使供应商的利润为0,即πsi(Xi,qi,pi,vi)=0,i=1,2。据此对模型 (4)进行转化,得到制造商的最优利润函数为:

将式(5)分解为两个独立问题,利用KT条件进行求解,可得定理3。
定理3:针对一个部分中断的主供应商和一个完全中断的次供应商,制造商的最优契约设计如表3所示。
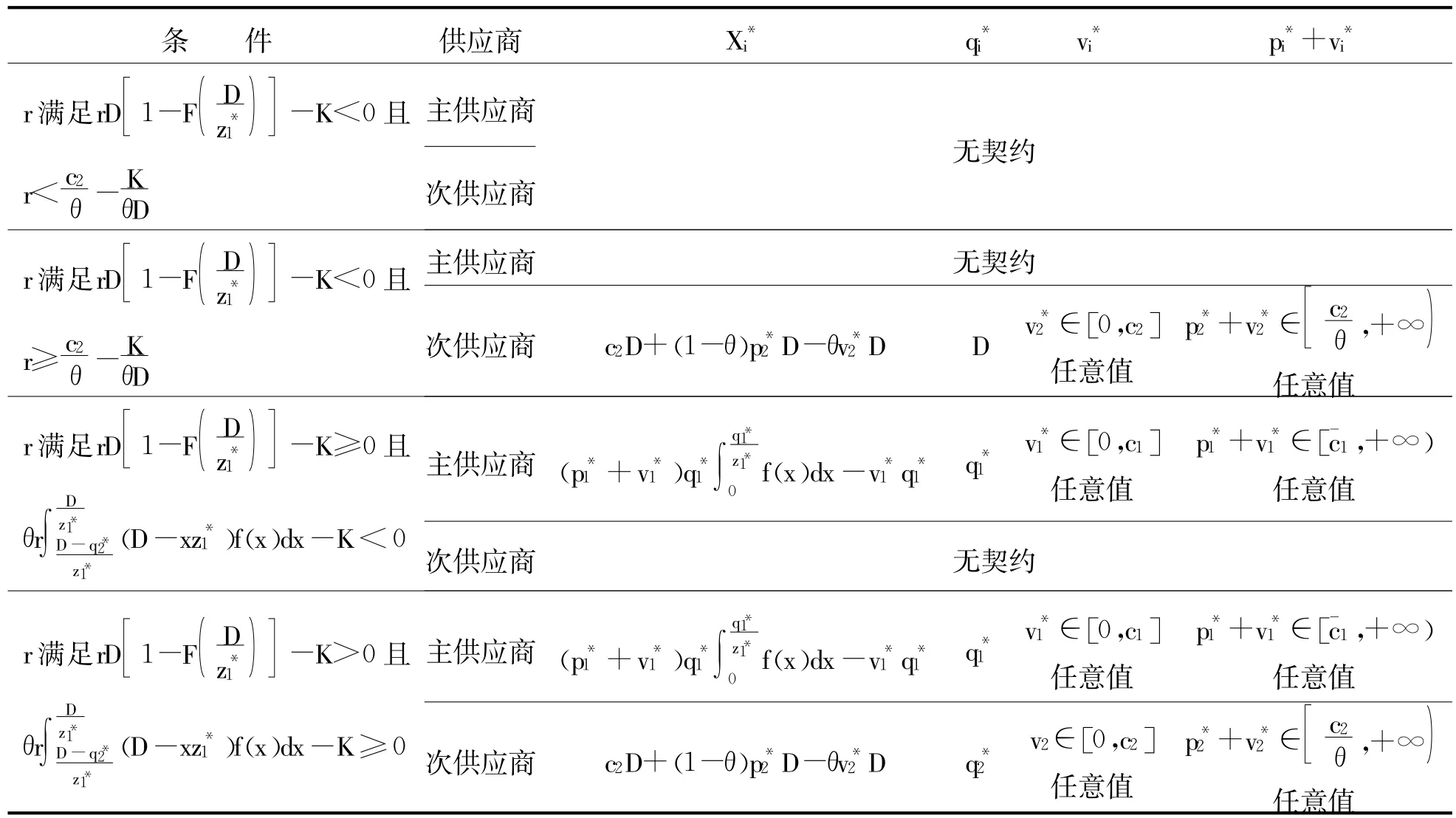
表3 制造商最优契约设计



3 主供应商的可靠性水平服从均匀分布下制造商的最优契约设计



表4 ρ1~U[0,m]时制造商的最优契约设计
从表4可以看出,供应商的固定支付与其自身的可靠性呈负相关。从制造商的角度看,供应商越可靠,提前支付的就越少,制造商也越愿意向其订货;相反,供应商越不可靠,就需要制定越大的惩罚成本,以尽量保证其交货量满足需求。当时,主供应商的订货量与需求量呈一定倍数关系;次供应商的订货量与其本身的可靠性呈正相关,与主供应商的可靠性呈负相关,即主供应商的可靠性越高,次供应商的可靠性越低,则次供应商的订货量越小,反之次供应商的订货量越大。事实上,主供应商可靠性越高,则其交货量越接近需求量,次供应商的订货量自然就越少;而次供应商的可靠性越低,制造商为使次供应商的交货量尽量满足需求,就需要更大的订货量。
4 算例分析
下面用一个算例对制造商的最优契约设计和供应商的最优生产规模进行模拟分析。由于第2小节所述情景并非都会出现,这不仅取决于零售价格的取值范围,还取决于限定的两个供应商的可靠性水平。受篇幅所限,本算例仅对零售商的可靠性水平做一种设定。
根据以上给定的数据,设定r变动范围为4~15,计算两个供应商的最优生产规模以及制造商的最优契约设计,结果如表5所示。

表5 供应商生产规模及制造商契约设计决策
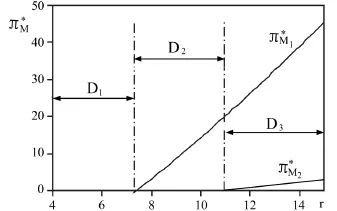
图2 零售价格与制造商从两个供应商处获得的利润之间的关系
从图2可知,制造商应根据产品零售价格的变化灵活地向供应商提供契约。D1部分表示制造商不与任何供应商签约,D2部分表示制造商只与主供应商签约,D3部分表示制造商与两个供应商同时签约。
5 结 论
已有的关于不可靠供应链契约设计的文献大都将供应商的可靠性分为高和低两种,本文引入可靠性服从随机分布的供应商,建立两阶段博弈的动态规划模型,以利润最大化为目标,运用逆序解法,得到供应商的最优生产规模以及制造商的最优契约设计。其中契约设计内容包括制造商给供应商的固定支付、订货量、变动支付及惩罚成本。制造商根据产品零售价格的变化灵活做出只与一个供应商签约、与两个供应商同时签约或都不签约的决定。研究还得出:供应商最优生产规模与产品的单位生产成本呈负相关,与单位变动支付和单位惩罚成本呈正相关;当主供应商的可靠性服从均匀分布时,主供应商的订货量与需求量呈一定的倍数关系;次供应商的订货量与其本身的可靠性呈正相关,与主供应商的可靠性呈负相关;供应商的固定支付与其相应的可靠性呈负相关;供应商的可靠性越低,惩罚成本应越高。
另外,本文只研究了需求确定的情况,下一步可以研究随机需求下的契约设计问题,还可以研究两个供应商的可靠性均服从连续的随机分布的情况,以及供应商的可靠性信息不对称时制造商的契约决策。
[1]Yang Z,Aydin G,Babich V,et al.Supply Disruptions,Asymmetric Information,and a Dual Sourcing Option[R].Working Paper.Industrial and Operations Engineering,University of Michigan,2008
[2]Yang Z,Aydin G,Babich V,et al.Supply Disruptions,Asymmetric Information,and a Backup Production Option[J].Management Science,2009,55(2):192~209
[3]Yang Z,Aydin G,Babich V,et al.Using a Dual-sourcing Option in the Presence of Asymmetric Information About Supplier Reliability:Competition vs.Diversification[J].Manufacturing&Service Operations Management,2012,14(2):202~217
[4]Sammi Y.Tang,Haresh Gurnani,Gupta D.Managing Disruptions in Decentralized Supply Chains With Endogenous Supply Process Reliability[J].Production and Operations Management,2014,23(7):1198~1211
[5]Wang Y,Gilland W,Tomlin B.Mitigating Supply Risk:Dual Sourcing or Process Improvement?[J].Manufacturing&Service Operations Management,2010,12(3):489~510
[6]Krause D R.Supplier Development:Current Practices and Outcomes[J].International Journal of Purchasing and Materials Management,1997,33(1):12~19
[7]Krause D R.The Antecedents of Buying Firms’Efforts to Improve Suppliers[J].Journal of Operations Management,1999,17(2):205~224
[8]Krause D R,Handfield R B,Tyler B B.The Relationships Between Supplier Development,Commitment,Social Capital Accumulation and Performance Improvement[J].Journal of Operations Management,2007,25(2):528~545
[9]Avinash Dixit,Susan Skeath,David Reiley.策略博弈 [M].第3版.北京:中国人民大学出版社,2012:263~267
[10]Ying-Ju Chen.Supply Disruptions,Heterogeneous Beliefs,and Production Efficiencies[J].Production and Operations Management,2014,23(1):127~137
[11]Tao Li,Sethi S P,Zhang J.How Does Pricing Power Affect a Firm’s Sourcing Decisions From Unreliable Suppliers?[J].International Journal of Production Research,2013,51(23-24):6990~7005
[12]黄松,杨超 .非对称成本扰动信息非线性需求函数下的供应链契约设计 [J].中国管理科学,2014,22(7):81~82
[13]王先甲,肖露,关旭 .非对称供应成本信息下装配系统定价与供货策略研究[J].系统工程理论与实践,2014,35(7):1689~1697
[14]Esmaeili M,Zeephongsekul P.Seller-buyer Models of Supply Chain Management With an Asymmetric Information Structure[J]. International Journal of Production Economics,2010,123(1):146~154
[15]王新辉,汪贤裕,苏应生 .双边成本信息不对称的供应链协调机制 [J].管理工程学报,2013,(4):196~204
[16]郑志欣,何波 .供应中断风险下链与链竞争的博弈分析[J].科技管理研究,2013,33(16):198~201
[17]Babich V,Burnetas A N,Ritchken P H.Competition and Diversification Effects in Supply Chains With Supplier Default Risk[J]. Manufacturing&Service Operations Management,2007,9(2):123~146
[18]Babich,Volodymyr,et al.Risk,Financing and the Optimal Number of Suppliers.Supply Chain Disruptions.Springer London,2012: 195~240
[19]Tomlin B.On the Value of Mitigation and Contingency Strategies for Managing Supply Chain Disruption Risks[J].Management Science,2006,52(5):639~657
[20]Tomlin B,Wang Y.On the Value of Mix Flexibility and Dual Sourcing in Unreliable Newsvendor Networks[J].Manufacturing& Service Operations Management,2005,7(1):37~57
[21]Dada M,Petruzzi N C,Schwarz L B.A Newsvendor’s Procurement Problem When Suppliers are Unreliable[J].Manufacturing&Service Operations Management,2007,9(1):9~32
[22]Li Q,Li B,Chen P,et al.Dual-channel Supply Chain Decisions Under Asymmetric Information With a Risk-averse Retailer[J].Annals of Operations Research,2015:1~25
[23]Chaturvedi A,Martínez-de-Albéniz V.Optimal Procurement Design in the Presence of Supply Risk[J].Manufacturing&Service Operations Management,2011,13(2):227~243
[24]Gümüs,M,Ray S,Gurnani H.Supply-side Story:Risks,Guarantees,Competition,and Information Asymmetry[J].Management Science,2012,58(9):1694~1714
Contracts Design of Dual Sourcing under Supply Disruption
Li Xinjun1,2Liu Xinghua1
(1.Yantai University,Yantai 264005,China;2.Dalian University of Technology,Dalian 116024,China)
This paper considers contracts designing for a two-stage chain consisting of a manufacturer and two suppliers.We treat the supplier of whose reliability obedient to random distribution as a main supplier,and treat the supplier of zero or all as a secondary supplier.Based on the profit maximization as the goal,establishing a dynamic programming model of a two-stage game-signing contracts stage and execution stage,we get the manufacturer’s optimal contract design.The manufacture makes a decision of signing contracts with only one supplier,both suppliers or neither according to the retail price of products,and the suppliers decide the optimal production scale based on the content of contracts.The research indicates that the optimal production scale shows as a negative correlation with per unit of the cost of production,and a positive correlation with per unit of variable payment and punishment cost.The order quantity of the secondary supplier presents a positive correlation with its own reliability,and a negative correlation with the reliability of the main supplier. The mixed payment has a negative correlation with its corresponding reliability.
supply disruption;contracts designing;dual sourcing option;reliability;two-stage supply chain
10.3969/j.issn.1004-910X.2016.12.005
F224.3
A
(责任编辑:王 平)
2016—03—19
国家社会科学基金项目 “基于供应商产能的供应应急策略与设计研究” (项目编号:12CGL042);国家自然科学基金项目“基于行为运作的加工系统干扰管理研究”(项目编号 :71271039);国家自然科学基金项目 “考虑有限理性的供应链中断风险管理模型研究”(项目编号:71272122)。
李新军,烟台大学经济管理学院副教授,大连理工大学管理与经济学部博士后。研究方向:应急管理,运作管理,物流与供应链管理。刘兴华,烟台大学经济管理学院硕士研究生。研究方向:物流与供应链管理、运营管理与应急管理的交叉学科。

