“天地合一”演绎宇宙和谐美

范青林

(山东省烟台市莱山区第一中学，山东 烟台 264003)



“天地合一”演绎宇宙和谐美

范青林

(山东省烟台市莱山区第一中学，山东 烟台 264003)

在“万有引力与航天”的教学中，不少教师发现学生对公式理解不透，不能很好地建立起物理模型，解题时找不到切入点.本文旨在对天体问题进行情景分类，挖掘物理公式背后的内涵和外延，建立起地面和空中两种物理模型，从而迅速破题.

地面模型；空中模型；天地合一；天体问题

随着我国航天技术的飞速发展，运用万有引力定律求解天体运动问题，成了高考的重要考查内容.在解答这类考题时，学生往往出现思维混乱，不能选用正确的公式求解，导致耗时多、得分少.原因在于许多教师在讲解这部分内容时，往往过分强调对知识结果的记忆及操练，而不深入分析知识的产生、形成过程，不重视知识间的引申与迁移，以致经常发出诸如“这问题已经做了好多次，也讲了好多次，为何还不会”的感慨.笔者认为要解决“讲了多次还不会”这个问题，必须对物理情景分类，建立起物理模型，从而帮助学生迅速找到破题方法.

例1：如图1所示，a为在赤道上相对地球静止的卫星，随地球自转做匀速圆周运动，b为沿地球表面附近做匀速圆周运动的人造卫星(轨道半径等于地球半径)，c为地球的同步卫星，以下关于a、b、c的说法中正确的是( ).

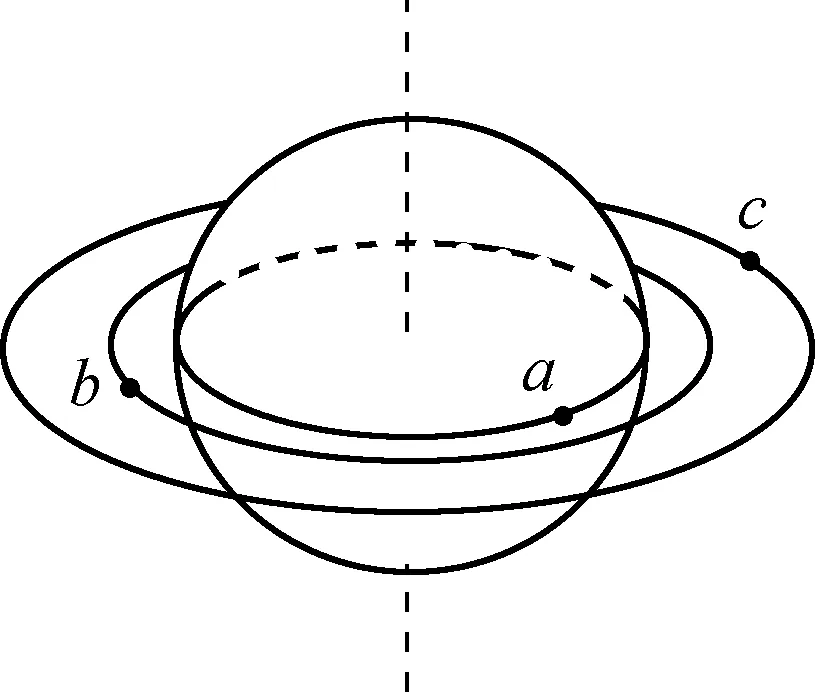
图1

A．a、b、c的向心加速度大小关系为ab>ac>aa

B．a、b、c的向心加速度大小关系为aa>ab>ac

C．a、b、c的线速度大小关系为va=vb>vc

D．a、b、c的周期关系为Ta=Tc>Tb

这是一道学生经常会出错的试题，究其原因，学生往往会把a、b、c三颗卫星一起根据万有引力充当向心力，去讨论相关参量的大小.笔者认为，学生犯错的关键在于对物理模型的理解模糊不清，分不清“地面模型”和“空中模型”，根据以上问题，现把两种模型建立的内涵和外延总结如下.

1 地面模型

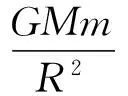
图2

例2：(2014年新课标全国卷Ⅱ)：假设地球可视为质量均匀分布的球体，已知地球表面的重力加速度在两极的大小为g0，在赤道的大小为g；地球自转的周期为T，引力常数为G，则地球的密度为( ).

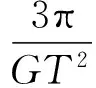
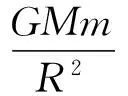
2 空中模型

图3

圆周运动各个参量大小与轨道半径的关系可以用一个口诀记忆：“高轨、低速(线速度、角速度、加速度)、大周期”.卫星在空中时，只受万有引力(重力)作用，并完全充当向心力，即万有引力=重力=向心力，口诀为“三力合一”.

例3：(2015年北京卷)：假设地球和火星都绕太阳做匀速圆周运动，已知地球到太阳的距离小于火星到太阳的距离，那么( ).

A． 地球公转周期大于火星的公转周期

B． 地球公转的线速度小于火星公转的线速度

C． 地球公转的加速度小于火星公转的加速度

D． 地球公转的角速度大于火星公转的角速度

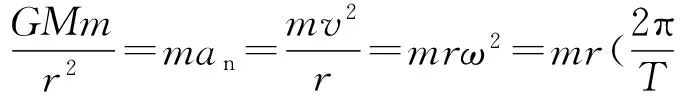
对于这两种模型的区别，从万有引力提供向心力的角度来说，“地面模型”是万有引力的一部分提供向心力，而“空中模型”是万有引力全部提供向心力.在图1中，a卫星在地面随地球一起自转，万有引力只有很小的一部分充当向心力；而b、c卫星在空中，万有引力全部充当向心力.

3 “天地合一”演绎和谐美

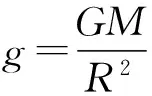
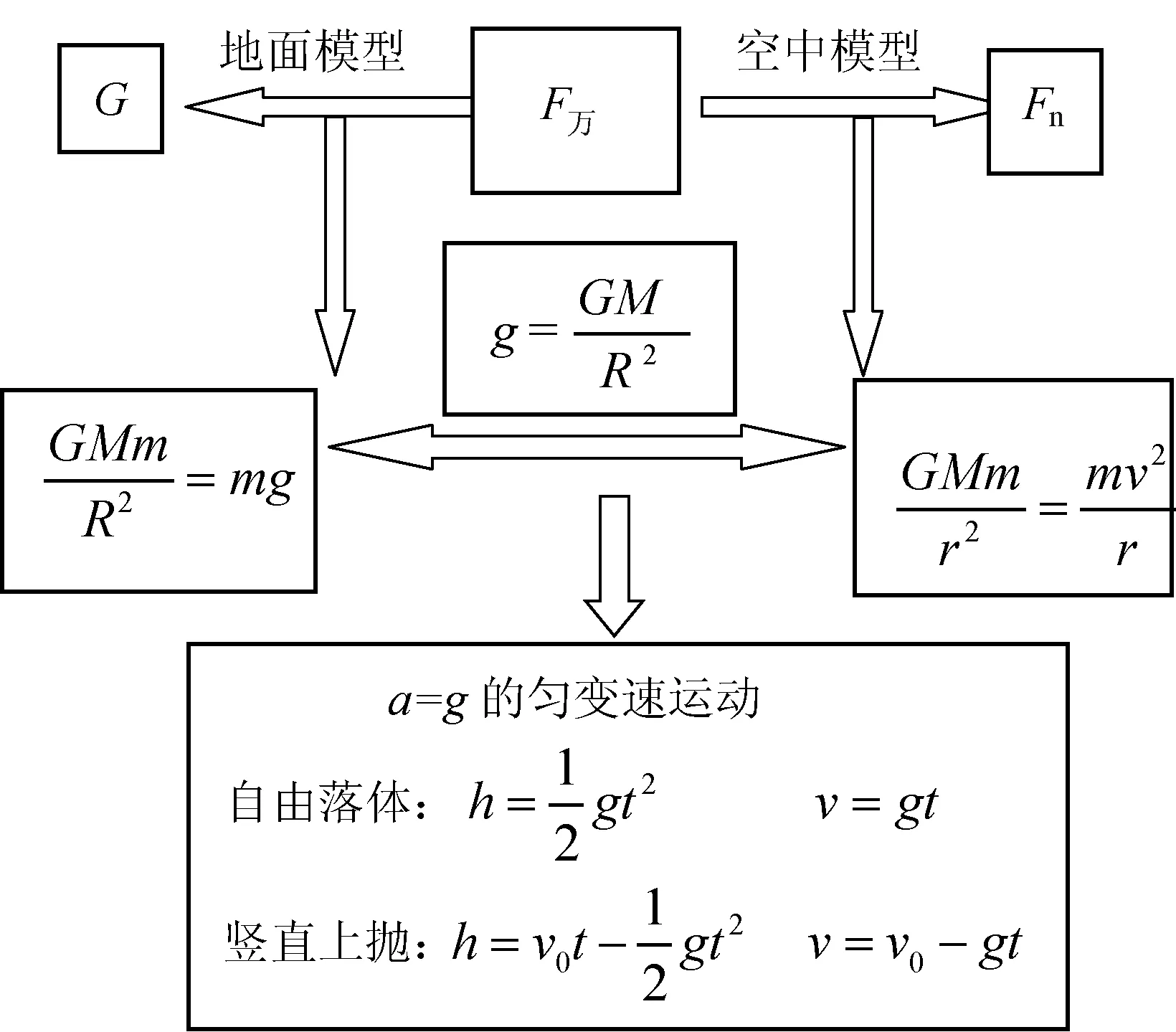
图4

例4：随着我国登月计划的实施，我国宇航员登上月球已不是梦想.假如我国宇航员登上月球并在月球表面附近以初速度v0竖直向上抛出一个小球，经时间t后回到出发点.已知月球的半径为R，万有引力常量为G，则下列说法正确的是( ).

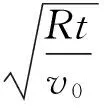
解析：本题涉及两个物理情景，即对应“地面模型”和“空中模型”.先是在月球表面竖直上抛，由运动学公式可以求出月球表面的重力加速度，再根据“地面模型”就可以求出月球质量.然后是发射宇航员绕月球表面做匀速圆周运动，对应的是“空中模型”，可以求出近月轨道的环绕速度和周期，容易得出正确答案选B.

可见，从试题的物理情景中找到对应的物理模型，然后根据对应模型的规律和公式，就能很容易找到试题的切入点而迅速破题.

对于天体问题，大部分试题都是以这两种模型为载体，同时结合变轨、人造卫星、宇宙速度等热点问题进行考查，如2015年新课标全国卷Ⅰ中有关天体问题的试题即是此类问题.因此深刻理解这两类模型建立的内涵和外延，恰当运用“地面模型”和“空中模型”对应的规律和公式即可迅速解题，从而帮助学生在高考中缩短做题时间，同时提升做题的正确率.