一类亚循环2-群自同构群的阶
杨艳
(湖北文理学院 数学与计算机科学学院,湖北 襄阳 441053)
一类亚循环2-群自同构群的阶
杨艳
(湖北文理学院 数学与计算机科学学院,湖北 襄阳 441053)
亚循环2-群是亚循环群中一种较为复杂的类型,讨论一类亚循环2-群的自同构群的阶.
亚循环群;亚循环2-群;自同构群
所谓亚循环群,就是循环群被循环群的扩张.关于亚循环群的研究,在分类和性质方面,从奇阶亚循环p-群到亚循环2-群,再到一般的亚循环群以及无限亚循环群,前人都做了卓有成效的研究.亚循环p-群的完全分类是由BruceW.King在1973年给出,而徐明曜利用奇阶亚循环p-群的正则性,把这一理论进行了简化计算.此后,随着对一些有特殊性质的p-群研究的深入,关于亚循环p-群的研究也不断涌现,这其中也包含很多对亚循环2-群的研究.[1-3]
关于亚循环群的自同构群,学者们通过对群的标准表示、群的内在结构以及群的阶的研究,给出了一些好的结果,包括分裂亚循环群、奇阶亚循环p-群、一些有特殊性质的亚循环群及无限亚循环群.在分裂的亚循环群方面,Curran M.J.利用亚循环群的标准表示及自同构群的阶,在2006及2007年发表了两篇文章,分别得到了分裂的奇阶亚循环p-群和亚循环2-群的自同构群.[4]
有限亚循环群的结构研究已完成,学者的注意力主要集中在其自同构群的研究上,而由Hall分解准则,一般亚循环群可分解为亚循环p-群,因此要得到一般亚循环群的自同构群,首先就要研究亚循环p-群的自同构群.奇阶的亚循环p-群的自同构群已由Curran M.J.给出,而亚循环2-群的自同构群的研究尚不全面.[5-6]
本文试图研究一类亚循环2-群的自同构群的阶,从而为研究其自同构群的结构提供支持.
1 相关定义及性质
引理1 有限亚循环2-群有两种表示,即

2 主要结论
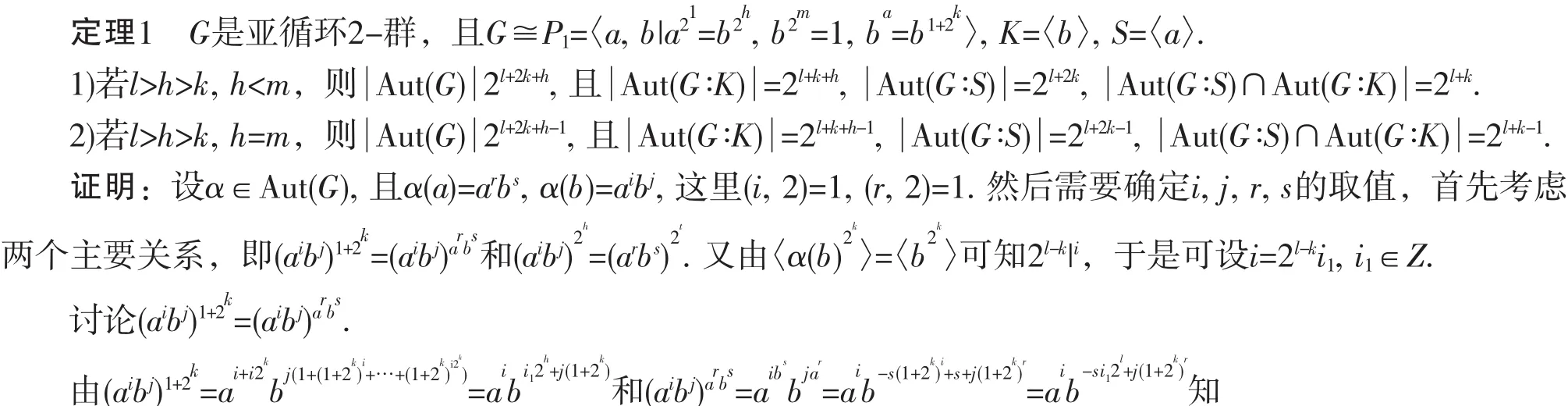


3 实例

4 结语
亚循环2-群是亚循环群中一种较为复杂的类型,本文讨论一类亚循环2-群自同构群的阶,并得到了其一部分自同构群的阶.文章研究方法和思路可用于讨论其它更复杂的亚循环2-群;根据亚循环2-群的自同构群的阶,结合文中推论,对研究其自同构群的结构有一定帮助.
[1]SIM HYOSEOB.Metacyclic groups of odd order[J].Bulletin of the Australian Mathematical Society,1993,47(2):47-71.
[2]HEMPEL C E.Metacyclic groups[J].Comm.Algebra,2000,28(8):3865–3897.
[3]XU MINGYAO,ZHANG QINHAI.A classification of metacyclic 2-groups[J].Algebra Colloq,2006,13(1):25-34.
[4]CURRAN M J.The automorphism group of a nonsplit metacyclic p-group[J].Arch.Math.,2008,90(6):483-489.
[5]杨 艳.有限分裂亚循环p-群一个判别条件[J].湖北文理学院学报,2013,34(8):8-9.
[6]杨 艳.亚循环p-群的表示[J].襄樊学院学报,2012,33(5):9-11
On the Order of the Automorphism Groups of Split Metacyclic 2-groups
YANG Yan
(School of Mathematical and Computer Sciences,Hubei University of Arts and Science, Xiangyang 441053,China)
The split metacyclic 2-groups are very important in group theory.In this paper,we give the order of the automorphism groups of split metacyclic 2-groups.
Metacyclic group;Metacyclic 2-group;Automorphism groups
O157
A
2095-4476(2016)11-0013-03
(责任编辑:饶 超)
2016-09-12
杨 艳(1981— ),女,湖北襄阳人,湖北文理学院数学与计算机科学学院讲师.

