博弈论在国际工程项目开发中的应用研究

张宝国，齐琦

（华电重工股份有限公司，北京100070）

博弈论在国际工程项目开发中的应用研究

张宝国，齐琦

（华电重工股份有限公司，北京100070）

结合博弈论探讨国际工程总承包企业在国际工程项目开发过程中的投标决策问题，建立投标决策最优理论模型,并据此对某国际工程项目投标决策进行实践，对从事国际工程项目的工程承包企业在投标报价决策上具有参考和借鉴作用。

博弈论；投标决策；国际工程；项目开发

【DOI】10.13616/j.cnki.gcjsysj.2016.08.114

1 引言

中国经济发展继续推动了工程建设行业的发展，而“走出去”、“一带一路”等政策则为拓展国际业务市场带来新的驱动力，为中国工程总承包企业涉足国际电力和基础设施等行业工程及建设市场创造了机会。国际工程项目基本采用竞争性招标、邀请招标和议标等方式选择项目的承包商，如何在激烈的市场竞争中寻求企业自身新的竞争优势，已成为国际工程参与企业的当务之急。在此背景下，探索在国际工程项目开发过程中涉及的竞争策略问题，从博弈论角度考虑投标过程中的定价决策已成为现实，为工程总承包企业在项目开发中提供了一种新的思路。

2 投标博弈概述

2.1 国际工程业务模式介绍

截至2015年12月，已有近4000家中国企业获得对外承包工程经营资格。在数量不断扩大的同时，中国对外承包工程企业的技术实力、管理能力得到不断提高，业务模式也从传统的施工总承包或EPC总承包为主转型到投资拉动的EPC工程总承包模式，包括通过小额投资入股获得项目建设权、公私合营（PPP）、建造转让（BT）、建造—运营—转让（B0T）等模式。在交通、房建、电力等领域业务继续扩大的同时，中国企业从事的国际工程领域也越来越广泛，扩展到矿产资源开发、房地产开发、农业开发项目、工业制造加工、垃圾及污水处理、纺织行业、装备制造行业等各个领域。

无论哪个业务领域、何种业务模式，目前国际工程项目大部分仍采用公开招标、邀请招标、竞争性谈判等形式确定工程项目承包商。由于国际工程项目的特殊性，其合同额少则几亿元，多则几十亿元，使得参与竞标的企业在技术水平、过往业绩、经营能力等方面不会有明显差别。

2.2 博弈论与投标

在公司业务规模、经营业绩、技术实力等方面相差不大的情况下，投标价格的高低往往成为中标与否的关键因素，因此如何在激烈的国际市场竞争中获得工程项目，已经不再局限于财力和技术等方面的较量，更多的是投标决策这种智力方面的较量。在完成项目成本估算后，如何确定工程项目投标总价即成为投标工作的核心，而最终投标报价是客户选择中标者的主要依据，直接影响投标成败。

博弈论是研究在利益相互影响的局势中，理性的局中人为了最大化自己的利益，如何选择各自的策略以及这种策略的均衡问题[1]。在国际工程项目招投标过程中，招标人与投标人、投标人与其他投标人之间都存在利益冲突。招标人的策略选择受到投标人的影响，投标人的策略选择也受招标人和其他投标人的影响。因此，国际工程项目竞争性招标就是招标人与投标人、投标人与投标人的博弈过程。

博弈论更加突出理性人的假定，以个人理性为基础，均衡概念越精炼，理性的要求也就越强。尽管现实中投标人的决策不一定完全符合博弈论中要求的高度理性，但是它为处于激烈竞争的国际工程项目市场中的参与者提供了制定投标报价决策的理论工具。

3 投标模型的建立与分析

在国际工程项目招投标过程中，招标方和投标方都是为了寻求个人的最大利益，属于非合作博弈。更近一步说，由于在国际工程项目招投标过程中投标人同时行动，没有机会了解别人的选择，而且每个投标人仅知道其他投标人类型的概率分布而不知道其真实类型，因此这种招投标形式属于不完全信息静态博弈，可以基于一次价格密封标价拍卖模型进行建模。

3.1 一次价格密封标价拍卖模型介绍

一次价格密封标价拍卖是指在所有竞拍者的报价中只有竞拍者本人和拍卖者知道，其他竞拍者不知道，只有报价最高者才能中标。

考虑只有2个竞拍者时，2个竞拍者对标的物的估价相互独立，并服从[0,1]区间上的均匀分布[2]，定义该博弈的基本式：

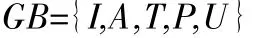
式中，I为参与者；A为行动空间；T为类型空间；P为信念；U为盈利函数。

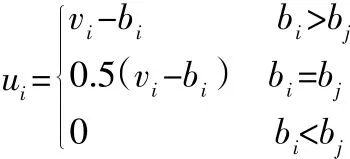
盈利函数ui为:式中，vi为竞拍者i对商品的估价；bi，bj分别为竞拍者i，j的报价，如中标则i的收益为vi-bi。

对[0，1]中的每一个vi、bi一 定满足:

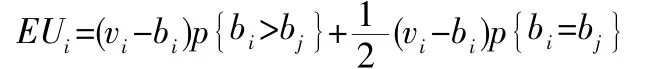
在多个竞拍者参与的情况下，竞拍者i的最优报价应满足：

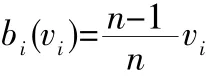
式中，EUi为投标者i的期望效用，n为任意自然数。

3.2 投标博弈模型建立

一次价格密封标价拍卖与目前国际工程项目投标有相似性，但也存在区别。一次价格密封标价拍卖中竞拍者寻求的是高于报价而低于竞拍品估价的价值，而国际工程投标的投标人寻求的是高于项目成本而低于报价的价值[3]。为此，我们需要根据一次价格密封标价拍卖模型重新建立投标博弈模型。

在各投标方公司业务规模、技术解决方案、建设期、质量保证等因素差别不大的情况下，招标方更多会考虑项目建设所需资金及融资规模而采用最低价中标模式[4]。对于只有2个投标者的成本分布函数博弈模型，投标者i盈利为:

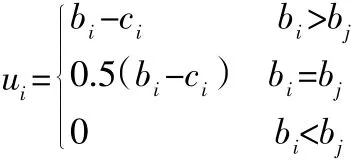
投标者i期望效用为:

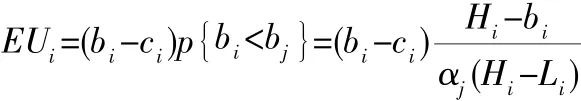
式中，bi为投标者i报价；ci为投标者i承包工程成本｝为bi＜bj概率；Hi是指投标人i估计的竞争者成本cj中可能的最高成本；Li是指投标人i估计的竞争者成本cj中可能的最低成本；αj是0～1之间的系数。

以效用最大化为目标一阶求导，解得的最优报价是:

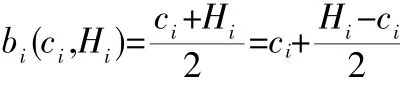
当投标者为多个时，最优解为：

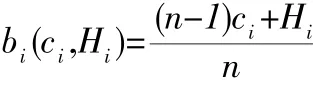
3.3 投标博弈模型分析

由纳什定理可知，投标报价博弈还属于有限博弈，至少存在一个纳什均衡解[5]，同时它又是不完全信息静态博弈，其均衡又称为“贝叶斯纳什均衡”。根据贝叶斯博弈进行决策的中心思想，每个投标者的策略行动必须是其他投标者策略行动的最佳反应[6]。基于博弈论的投标报价模型更偏重于针对竞争局势，通过求解均衡在可能的报价集中寻求一个确切的最佳报价点，实现自身的利益最大化。

4 投标博弈模型的工程实践

H公司在2015年参加了南非伊丽莎白港某矿石出口码头建设工程总承包项目投标，该项目范围包括海域装船系统、陆域堆场系统、火车翻卸系统、各系统间的连接输送系统及所有土建施工的设计、供货、建造和安装、调试等工作。项目建设周期3年，工程预算约17亿人民币。参与投标的企业为包括H公司在内的6家中国工程总承包企业、5家欧洲公司和4家南非当地公司。考虑各公司规模和实力，在满足基本投标条件的前提下，H公司的真正竞争对手是4家中国公司和4家欧洲公司。包括H公司在内的9家公司在投标技术方案上不会有很大的差别，更多差别还是在成本控制和项目执行管理方面的竞争力。评标方式为评标委员会参与的综合评分法，如综合评分在一定范围内相同，则采用最低价中标方式。

H公司在编制完成整个项目的解决方案及成本预算后，确定此项目总成本预算约为15.86亿元。按以上建立的投标博弈模型，结合以往各竞争对手报价情况，可得数据如表1所示。

表1 各竞争对手报价成本估算亿元

结合各竞争对手在本项目中的期望，估算出最优投标报价为：

根据贝叶斯纳什均衡，将最优投标报价调整为16.15亿元。考虑项目的合理利润、中标后项目执行过程中的确定性和不确定性风险的影响，确定最终报价为16.845亿元。项目开标后，各家报价情况基本与估算最高成本一致，H公司报价为9家相似规模和能力公司提供报价的最低价。经客户评标委员会结合公司业绩、运营情况及对各竞争公司总部及主要供货商/工厂的管理能力、生产制造能力、质量控制能力等情况考察评估后，确定H公司中标。

5 投标博弈模型应用分析

由博弈论最优报价公式可知,投标人最优报价跟自身的成本、参与投标人数、投标人对其他投标人投标估价等因素有关。投标人的自身投标成本是可以确定的,随着参与投标人数的增加,最优报价也随着降低,利润也随之减少,当n→∞,b→c时,即投标人无限多时，最优报价为投标人自己的成本。

在论文所述南非伊丽莎白港矿石出口码头建设工程总承包项目投标实践中,博弈论模型得到了充分应用,取得了良好效果。在越来越多的竞争者参与的工程招投标市场中,投标人在保证成本和基本利润情况下报尽可能的低价是招投标各方博弈的必然结果。然而，需要注意的是，如果国际工程项目的投标报价接近成本预算,在部分风险较高的项目所在国,很可能导致项目决算时亏损。因此，在具体报价过程中，除按此方法预测外还要根据对可控风险及未知风险的估计而最终确定项目投标最终报价，才能保证项目的预算利润。

【1】谢识予.经济博弈论[M].上海：复旦大学出版社，2002.

【2】张维迎.博弈论与信息经济学[M].上海：上海人民出版社，1996.

【3】国际咨询工程师联合会中国工程咨询协会.设计采购施工（EPC）/交钥匙工程合同条件[M].北京：机械工业出版社，2005.

【4】国际咨询工程师联合会中国工程咨询协会.生产设备和设计-施工合同条件[M].北京：机械工业出版社，2002.

【5】崔军.FIDIC分包合同管理与实务[M].北京：机械工业出版社，2010.

【6】王伍仁.EPC工程总承包管理[M].北京：中国建筑工业出版社，2008.

The Application of Game Theory in Development of International Projects

ZHANG Bao-guo,QI Qi
（Huadian Heavy Industries Co.Ltd.,Beijing100070,China)

This paper discusses the bidding decision-making of general contracting enterprises in developing international projects,and the optimal theoretical model of bidding decision is established.According to that,it was carried out in the bidding decision-making of an international project,providing a reference to engineering enterprises on bidding decision-making.

game theory；bidding decision；international projects；project development

F224.32;TUT23.2

A

1007-9467（2016）08-0209-02

2016-07-27

张宝国（1982～），男，黑龙江绥化人，从事矿山、港口等行业物料输送系统设计与项目管理研究。