吊桥型方程强指数吸引子的存在性

汪 璇,张玉宝，胡弟弟

(西北师范大学数学与统计学院,甘肃兰州 730070)



吊桥型方程强指数吸引子的存在性

汪 璇,张玉宝，胡弟弟

(西北师范大学数学与统计学院,甘肃兰州 730070)

研究吊桥型方程在强拓扑空间中的长时间动力学行为,运用一些新方法得到了强指数吸引子的存在性.

吊桥型方程;强拉平性;强指数吸引子

0 引言

本文考虑吊桥型方程

(1)

的强指数吸引子.1990年,Lazer和McKenna在非线性分析领域提出吊桥模型(1),该模型起源于吊桥系统,在系统中,吊桥被视为两端具有铰链的弹性无负荷梁,u(x,t)表示向下的位移,δut表示粘性阻力.根据胡克定律,在一端钢缆的作用下恢复力可以对抗拉伸但是不能对抗压缩.用常数k乘以u+来表示吊桥的恢复力,拉伸时u为正,u+等于u,压缩时u为负,u+等于0,即

此外,(1)式右端还包含两项:大的正项l(对应于重力)以及源于空气动力学的小的震荡外力项εh(x,t),其中ε为很小的正数.

关于问题(1)的研究已经有许多结果[1-7],例如行波解的存在性、多重性等等.

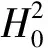
(2)

其中u(x,t)为未知函数,它表示桥床在垂直平面的位移;h(x)为外力项;ku+为恢复力,k为弹力系数;αut表示粘性阻尼,α为给定的正常数.

为简便起见,C(或Ci)表示任意正常数.

1 符号和预备知识

显然,我们有

D(A)⊂V⊂H=H*⊂V*,

其中H*,V*分别为H,V的对偶空间,映射连续且每一个空间在其后空间中是稠密的.

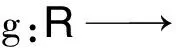
(3)

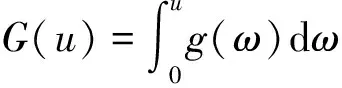
(4)

设γ为任意正常数,且

(5)

根据(3)～(4)式,若Λ(u)=∫ΩG(u)dx,则存在两个正常数K1,K2,使得

(6)

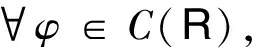
(7)

其中m,C0>0,并且m充分小.

根据(5)式,可得

(8)

当 A=Δ2时,问题(2)在空间H中等价于方程

(9)

根据Poincaré不等式,存在常数λ1>0,使得

(10)

引入Hilbert空间E0=V×H,E1=D(A)×V,并且赋予范数

为了证明方程(9)指数吸引子的存在性,我们需要以下结果,参见文献[8,10,11,13-19].

定义1[13]设X为Banach 空间,{S(t)}t≥0为X上的映射族.称{S(t)}t≥0为X上的弱范连续半群,如果{S(t)}t≥0满足

( i )S(0)=Id;

( ii )S(t)S(s)=S(t+s),∀t,s≥0;

(iii)若tn→t,xn→x，则S(tn)xn⇀S(t)x.

定理1[13]设X,Y满足上述假设,{S(t)}t≥0为Y中的连续或弱连续半群,且将X×R+中的紧子集映射到X中的有界集,则称{S(t)}t≥0是X上的弱范连续半群.

定理2[11]设k>0,且(3)～(5)式成立,如果h∈H,u1∈V,u2∈H,则方程(9)存在唯一解u,使得u∈C([0,T];V),ut∈C([0,T];H),∀T>0.进一步,映射(u1,u2)→(u(t),ut(t))在E0=V×H上连续.所以,定义C0半群S(t):(u1,u2)→(u(t),ut(t)),t∈R+,则{S(t)}t≥0映射E0到其自身.

通常({S(t)}t≥0,X)称为一个动力系统.集合B称为({S(t)}t≥0,X)的有界吸收集,如果对于任意有界集B0⊂X,存在t0=t0(B0),使得S(t)B0⊂B,∀t≥t0.集合D称为关于{S(t)}t≥0正不变的,如果对∀t≥0,有S(t)D⊂D.

集合A⊂X称为({S(t)}t≥0,X)的全局吸引子,如果

( i )A在X中紧;

( ii )S(t)A=A,∀t≥0;

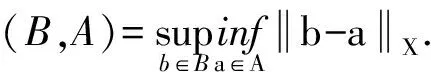
定义2[8,10,14]设n(M,ε)(ε>0)表示在空间X中用半径为ε的球覆盖M的球的最小个数,则M的分形维数为

(11)

定义3[15-18]设{S(t)}t≥0为完备度量空间X中的半群.集合M⊂X称为半群{S(t)}t≥0的指数吸引子,如果:

( i )集合M在X中紧且有有限的分形维数;

( ii )集合M为正不变的,即S(t)M⊂M；

(iii)集合M为半群{S(t)}t≥0的指数吸引集,即对于每一个有界子集B⊂X,存在常数k=k(B)>0,l>0,使得dist(S(t)B,M)≤ke-lt.

定理3[19]设B为{S(t)}t≥0在空间X中的有界吸收集,则以下结论等价:

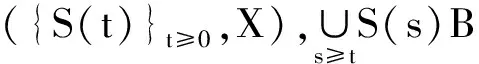
(ii)半群{S(t)}t≥0存在指数吸引子.

定义4[19](强拉平性) 设X为一致凸Banach空间,对于任意有界集B⊂X,存在k,l,T>0及X的有限维子空间X1,使得

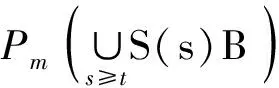
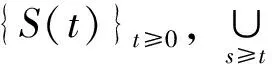
定理5[19]设X为一致凸Banach空间,且{S(t)}t≥0在X中为连续或强弱连续半群,则{S(t)}t≥0存在指数吸引子,如果下列条件成立:

( i )存在有界吸收集B⊂X;

( ii ){S(t)}t≥0满足强拉平性.

2 空间E1中的指数吸引子

2.1 解的存在唯一性

首先给出初-边值问题(9)的强解概念.

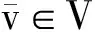
(12)

应用Galerkin逼近方法[20],我们可以得到以下强解的存在唯一性结果:

定理6(强解的存在唯一性) 对∀T>0,定义I=[0,T].设k>0,h∈V,g∈C2(R;R)满足(3)～(5)式且g(0)=0,则对于任意给定的z0∈E1,问题(9)在空间E1中存在唯一强解z=(u,ut)∈L∞(I;E1).进一步,z=(u,ut)从I到E1是弱连续的.

2.2E1中的一致有界吸收集

定理7[12](一致有界吸收集) 设k>0,h∈V,g∈C2(R;R)满足(3)～(5)式,则半群{S(t)}t≥0在E1中存在有界吸收集.

2.3 E1中指数吸引子的存在性

首先需要以下半群的强弱连续性和紧性结果.

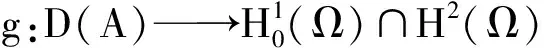
由定理6,在E1中定义

(13)

则半群{S(t)}t≥0将E1映入E1.

引理2[12]由(13)式定义的半群{S(t)}t≥0在E1中是强范连续的.

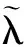
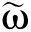
其中(u1,u1t)=(Pmu,Pmut).

引理3 设k>0,h∈H,g∈C3(R;R)满足(3)～(5)式,{S(t)}t≥0为问题(9)的解半群,则半群{S(t)}t≥0在空间E1中满足强拉平性,即对E1中任意的有界集B,存在k,l,T>0和函数q(m),使得对任意的z0∈B,t≥T,有

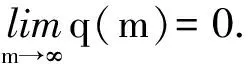
证明 选取0<ρ<1,且0<ρ(α-ρ)<λ1.用Av2(t)=Au2t(t)+ρAu2(t)与(9)式在空间H上作内积,可得

(14)

其中

(15)

(16)

显然,我们可以得到

(17)

(18)

结合(15)～(18)式,根据(14)式可得

(19)

定义泛函:

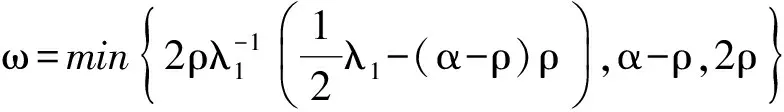
(20)

(21)

(22)

所以

(23)

由Gronwall引理可得

(24)

故

(25)

因此,问题(9)的解半群{S(t)}t≥0在空间E1中满足强拉平性. 】

结合定理7、引理2和引理3,由定理5我们可以得到以下结果:

定理8(强指数吸引子) 设k>0,h∈V,g∈C3(R;R)满足(3)～(5)式,{S(t)}t≥0为问题(9)的解半群,则半群{S(t)}t≥0在空间E1中拥有指数吸引子.

[1] AN Y K,ZHONG C K.Periodic solutions of a nonlinear suspension bridge equation with damping and nonconstant load[J].JMathAnalAppl,2003,279(2):569.

[2] CHOI Q H,JUNG T.A nonlinear suspension bridge equation with nonconstant load[J].NonlinearAnal,1999,35(6):649.

[3] HUMPHREYS L D.Numerical mountain pass solutions of a suspension bridge equation[J].NonlinearAnal(TMA),1997,28(28):1811.

[4] LAZER A C,MCKENNA P J.Large-amplitude periodic oscillations in suspension bridge:Some new connections with nonlinear analysis[J].SiamRev,1990,32(4):537.

[5] LAZER A C,MCKENNA P J.Large scale oscillatory behavior in loaded asymmetric systems[J].AnnalesDeLInstitutHenriPoincareNonLinearAnalysis,1987(3):243.

[6] MCKENNA P J,WALTER W.Nonlinear oscillation in a suspension bridge[J].NonlinearAnal,2000,39:731.

[7] MA Q Z,ZHONG C K.Existence of global attractors for the coupled system of suspension bridge equations[J].JMathAnalAppl,2005,308:365.

[8] CHEPYZHOV V V,VISHIK M I.AttractorsforEquationsofMathematicsandPhysics[M].Rhode Island:American Mathematical Society Colloquium Publication,2002.

[9] HALE J K.AsymptoticBehaviorofDissipativeSystems[M].Providence,Rhode Island:Amer Math Soc,1988.

[10] TEMAM R.Infinite-DimensionalDynamicalSystemsinMechanicsandPhysics[M].New York:Springer,1997.

[11] MA Q Z,ZHONG C K.Existence of global attractors for the suspension bridge equations[J].JSichuanUniv,2006,43(2):271.

[12] ZHONG C K,MA Q Z,SUN C Y.Existence of strong solutions and global attractors for the suspension bridge equations[J].NonlinearAnal,2007,67(2):442.

[13] ZHONG C K,YANG M H,SUN C Y.The existence of global attractors for the norm-to-weak continuous semigroup and application to the nonlinear reaction-diffusion equations[J].JournalofDifferentialEquations,2006,223(2):367.

[14] LADYZHENSKAYA O.AttractorsforSemigroupandEvolutionEquations[M].Cambridge:Cambridge University Press,1991.

[15] EDEN A,FOIAS C,NICOLAENKO B,et al.ExponentialAttractorsforDissipativeEvolutionEquations[M].Research in Applied Mathematics,vol.37.New York:John Wiley,1994.

[16] GRASSELLI M D.Exponential attractors for a class of reaction diffusion problems with time delays[J].JEvolEqu,2007,7(4):649.

[17] DUNG L,NICOLAENKO B.Exponential attractors in Banach spaces[J].JDynamDifferentialEquations,2001,13(4):791.

[18] ZHONG Y S,ZHONG C K.Exponential attractors for reaction-diffusion equations with arbitrary polynomial growth[J].NonlinearAnal,2009,71:3.

[19] LI Y,WU H,ZHAO T.Necessary and sufficient conditions for the existence of exponential attractors for semigroups,and applications[J].NonlinearAnal,2012,75(17):6297.

[20] BORINI S,PATA V.Uniform attractors for a strongly damped wave equations with linear memory[J].AsymptotAnal,1999,20(3/4):263.

(责任编辑 马宇鸿)

The existence of strong exponential attractors for suspension bridge-type equations

WANG Xuan,ZHANG Yu-bao,HU Di-di

(College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,Gansu,China)

The long-time dynamical behavior is discussed for the suspension bridge-type equation in the strong topological space.Moreover,the existence of strong exponential attractor is obtained by applying a new semigroup scheme.

suspension bridge equation;enhanced flattening property;strong exponential attractor

10.16783/j.cnki.nwnuz.2016.06.003

2016-01-17;修改稿收到日期:2016-07-13

国家自然科学基金资助项目(11361053,11261053)；甘肃省自然科学基金资助项目(145RJZA112)

汪璇(1973—)，女，山东临清人，副教授，博士．主要研究方向为应用微分方程和无穷维动力系统．

E-mail:wangxuan@nwnu.edu.cn

O 175.27;O 175.29

A

1001-988Ⅹ(2016)06-0013-05