有限维幂零Hom-李代数的分类

陈 雪，韩 伟

(1.厦门理工学院应用数学学院，福建厦门 361024；2.上海交通大学数学科学学院，上海 200240)



有限维幂零Hom-李代数的分类

陈 雪1，韩 伟2

(1.厦门理工学院应用数学学院，福建厦门 361024；2.上海交通大学数学科学学院，上海 200240)

首先研究了幂零和可解Hom-李代数的一些性质，将经典有限维李代数的可解和幂零的一些结果推广到Hom-李代数上，其次分类了四维和五维幂零Hom-李代数，根据Hom-李代数的半中心的维数，可以将四维和五维幂零Hom-李代数分为3种和4种不同类型.

Hom-李代数；幂零性；分类

0 引言

2006年，Hartwig等为了构造Witt 和 Virasoro代数的形变，引入了Hom-李代数的结构[1].一个Hom-李代数就是一个三元对(g,[·,·]，α),其中α是g上的线性映射，反对称双线性运算[·,·]满足α-扭不变的Jacobi等式，称为Hom-Jacobi等式.当α是恒等映射时，Hom-Jacobi等式退化为一般的Jacobi等式，此时g就是一个李代数.由于Hom-李代数在离散和形变向量场、微积分、Yang-Baxter方程等方面有很多应用，因此最近关于Hom-李代数的研究越来越深入[2-7].

Yau研究了Hom-李代数的包络代数的构造及其性质[7].Jin等研究了半单李代数上的Hom-李代数结构，他们指出有限维单李代数没有任何非平凡的Hom-李代数结构，并且给出了有限维半单李代数具有非平凡Hom-李代数结构的充要条件[8].后来Benayadi等[2]又构造了具有对称不变非退化双线性型的Hom-李代数.Hom-李代数表示部分的研究也有了很大进展，Sheng[3]研究了Hom-李代数的伴随和平凡表示.

本文的目的是研究幂零Hom-李代数.主要结构如下：第1部分列出了一些关于Hom-李代数的基本定义；第2部分给出幂零和可解Hom-李代数的一些性质；第3部分分类了四维幂零Hom-李代数；第4部分分类了部分五维幂零Hom-李代数.本文如非特别说明，所有代数都是有限维的,并且定义在特征为零的代数闭域C上.

1 预备知识

定义1[1-9]Hom-李代数是一个三元对(g,[·,·]，α)，由线性空间g，双线性映射[·,·]：g×g→g，及线性映射α:g→g组成，满足下列条件：

(1)[x,y]=-[y,x] (反对称性)，

(2)对所有x,y,z∈g，有Hom-Jacobi等式，

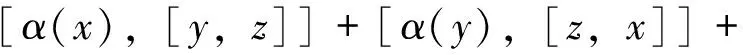
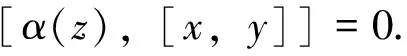
在上述定义中，若α是代数同态，即，对任意x,y∈g，有α([x,y])=[α(x),α(y)],则称(g,[·,·]，α)为保积Hom-李代数.

定义2 设(g,[·,·]，α)是一个Hom-李代数，η是g的一个子空间，若α(η)⊆η, [η,η]⊆η，则称(η,[·,·]，α)为Hom-李子代数.特别地，若[η,g]⊆η，则Hom-李子代数(η,[·,·]，α)称为(g,[·,·]，α)的理想.若对任意x,y∈g，有[x,y]=0，则称(g,[·,·]，α)为交换Hom-李代数.

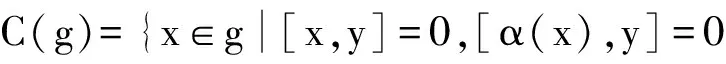
命题1 设(g,[·,·]，α)是一个保积Hom-李代数，则(Ker(α),[·,·]，α)是一个理想.

证明 显然对任意x∈Ker(α)，有α(x)=0∈Ker(α).由于对任意x∈Ker(α),y∈g，有α([x,y])=[α(x),α(y)]=[0,α(y)]=0，得到[x,y]∈Ker(α)，因此(Ker(α),[·,·],α)是(g,[·,·]，α)的一个理想. 】

定义4[8]设(g1,[·,·]，α)和(g2,[·,·]，β)是两个Hom-李代数，设φ:g1→g2是一个线性映射，如果对任意x,y∈g1，有

则称φ是一个Hom-李代数同态.特别地，当φ是一个双射时，Hom-李代数(g1,[·,·]1，α)和(g2,[·,·]2，β)同构.

定义5 设(g,[·,·]，α)是一个Hom-李代数，如果(g,[·,·]，α)没有非平凡理想并且[g,g]=g，则称(g,[·,·]，α)为单Hom-李代数.如果(g,[·,·]，α)可以分解为一些单理想的直和，则称(g,[·,·]，α)为半单Hom-李代数.

2 Hom-李代数的可解性和幂零性

定义6 设(g,[·,·]，α)是一个Hom-李代数，η是g的一个子空间，若[η,η]⊆η，则称η为(g,[·,·]，α)的一个半子代数.特别地，若[η,g]⊆η，则η称为(g,[·,·]，α)的半理想.

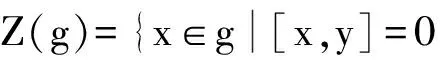
显然C(g)⊆Z(g)，那么何时C(g)=Z(g)成立呢？下面的命题给出了答案.

命题2 设(g,[·,·]，α)是一个Hom-李代数，给出C(g)=Z(g)成立的充分条件，

(1)对任意x,y∈g，α([x,y])=[α(x),y]；

(2)[g,g]=g;

(3)α是(g,[·,·]，α)的一个自同构；

(4)α是(g,[·,·]，α)的一个自同态，并且g=Z(g)+Im(α).

证明 显然由(1)可以推出C(g)=Z(g)成立.

(2)对任意x∈Z(g),y∈g，存在u,v∈Z(g)使得[u,v]=y，则[α(x),y]=[α(x),[u,v]]=-[α(u),[v,x]]-[α(v),[x,u]]=0，因此x∈C(g).

(3)对任意x∈Z(g),y∈g，由于[α(x),y]=α([x,α-1(y)])=0，于是有x∈C(g).

(4)对任意x∈Z(g),y∈g，存在u∈g,v∈Z(g),使得y=α(u)+v,则[α(x),y]=[α(x),α(u)+v]=α([x,u])=0，因此x∈C(g). 】

定义8 设(g,[·,·]，α)是一个Hom-李代数，定义导出列：g(0)=g，g(1)=[g,g],g(2)=[g(1),g(1)],…,g(i)=[g(i-1),g(i-1)].如果存在g(n)=0， 则称Hom-李代数(g,[·,·]，α)是可解的.定义降中心列：g0=g,g1=[g,g],g2=[g,g1],…,gj=[g,gi-1].如果存在gn=0， 则称Hom-李代数(g,[·,·]，α)是幂零的.

显然幂零Hom-李代数是可解的，而且导出列和降中心列的各项以及Z(g)都是半理想.对Hom-李代数(g,[·,·]，α)，由于可解性和幂零性都是用运算[·,·]定义的，没有用到线性映射α，那么我们能够很自然地将有限维李代数的可解和幂零的一些结果推广到Hom-李代数上.

命题3 设(g,[·,·]，α)是一个Hom-李代数，

(1)如果(g,[·,·]，α)是可解的，则g的所有半子代数和同态像也是可解的.

(2)如果η是g的一个可解的半理想并且g/η可解，则g也是可解的.

(3)如果η1和η2是g的一个可解的半理想，则η1+η2也是可解的.

命题4 设(g,[·,·]，α)是一个Hom-李代数，

(1)如果(g,[·,·]，α)是幂零的，则g的所有半子代数和同态像也是幂零的.

(2)如果g/Z(g)是幂零的，则g也是幂零的.

(3)如果g是幂零的且非零，则Z(g)≠0.

3 四维幂零 Hom-李代数的分类

本部分我们总是假设(g,[·,·]，α)是四维幂零Hom-李代数，则根据命题4(3)知道Z(g)≠0.因此根据dim(Z(g))，四维幂零Hom-李代数至多可以分为3类：

(Ⅰ)dim(Z(g))=4(或3);

(Ⅱ)dim(Z(g))=2;

(Ⅲ)dim(Z(g))=1.

显然我们有下面的结论.

定理1 设dim(Z(g))=4(或3)，则四维幂零Hom-李代数(g,[·,·]，α)是交换的.设(g1,[·,·]，α)和(g2,[·,·]，β)是2个四维幂零Hom-李代数且dim(Z(g1))=dim(Z(g2))=4(或3)，设A(或B)是α(或β)在g1(或g2)的任意一组基下对应的矩阵，则2个四维幂零Hom-李代数(g1,[·,·]，α)和(g2,[·,·]，β)同构当且仅当A和B是相似矩阵.

证明 显然由假设条件可以得到结论. 】

定理2 设dim(Z(g))=2.

(1)对四维幂零Hom-李代数(g,[·,·]，α)，可以选择一组基{x1,x2,x3,x4}，使得方括号运算满足[x3,x4]=x1，其余为零.

(2)设g=Cx1⊕Cx2⊕Cx3⊕Cx4是一个复数域上的向量空间，定义方括号运算：[x3,x4]=x1，其余为零，则对g上的任意线性映射α，(g,[·,·]，α)是四维幂零Hom-李代数.

(3)由向量空间g，(2)中方括号运算和g上的线性映射α1和α2定义的四维幂零Hom-李代数(g,[·,·]，α1)和(g,[·,·]，α2)同构当且仅当存在φ∈Ψ，使得φ∘α1=α2∘φ，其中

Ψ={φ是g上的可逆线性映射：

证明 (1)当dim(Z(g))=2，显然可以得到dim([g,g])=1,并且[g,g]⊆Z(g).因此可以选择两个非零向量x1∈[g,g],x2∈Z(g)使得{x1,x2}线性无关，然后将{x1,x}扩充为g的一组基{x1,x2,x3,x4}使得方括号运算为[x3,x4]=x1，其余为零.

(2)对g上的任意线性映射α，显然Hom-Jacobi等式成立，因此 (g,[·,·]，α)是Hom-李代数，由方括号运算，显然g2=0，所以(g,[·,·]，α)是幂零的.

(3)由(2)，对g上的任意线性映射α1和α2，(g,[·,·]，α1)和(g,[·,·]，α2)都是四维幂零Hom-李代数.设φ是g上的可逆线性映射，容易验证对任意x,y∈g,φ([x,y])=[φ(x),φ(y)]，当且仅当

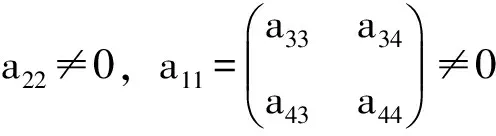
定理3 设dim(Z(g))=1.

(1)则dim([g,g])=2，可以选择四维幂零Hom-李代数(g,[·,·]，α)的一组基{x1∈Z(g),x2,x3,x4}，使得方括号运算满足[x2,x3]=x1,[x3,x4]=x2，其余为零.

(2)设g=Cx1⊕Cx2⊕Cx3⊕Cx4是复数域上的向量空间，定义方括号运算：[x2,x3]=x1,[x3,x4]=x2，其余为零.则对任意α∈Φ，(g,[·,·]，α)是一个四维幂零Hom-李代数，其中

Φ={α是g上的线性映射:

*表示任意复数}.

(3)由向量空间g，(2)中方括号运算以及g上的线性映射α1和α2(α1,α2∈Φ)定义的四维幂零Hom-李代数(g,[·,·]，α1)和(g,[·,·]，α2)同构,当且仅当存在φ∈Γ，使得φ∘α1=α2∘φ，其中

Γ={φ是g上的可逆线性映射:

证明 (1)当dim(Z(g))=1，显然dim([g,g])≤3，如果dim([g,g])=3，则g不是幂零的，与已知条件矛盾.

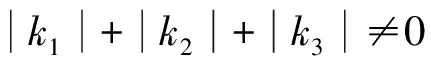
如果dim([g,g])=2，则根据g的幂零性,显然有Z(g)⊂[g,g].因此可以选择[g,g]的一组基{x1∈Z(g),x2}并将其扩充为g的一组基{x1,x2,x3,x4}.设

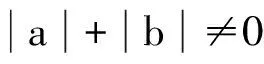
(2)设α是g上的一个线性映射，显然α只需要对x1,x3,x4和x2,x3,x4满足Hom-Jacobi等式即可，即

由方括号运算，上面的算式可以化简为

因此

则α满足Hom-Jacobi等式当且仅当α∈Φ，所以推出(g,[·,·]，α)是Hom-李代数，另外g3=0，故g是幂零的.

(3) 由(2)，对线性映射α1,α2∈Φ，(g,[·,·]，α1)和(g,[·,·]，α2)都是四维幂零Hom-李代数.设φ是g上的可逆线性映射，容易验证对任意x,y∈g,φ([x,y])=[φ(x),φ(y)]当且仅当

其中a11a22≠0.因此φ是(g,[·,·]，α1)到(g,[·,·]，α2)的同构,当且仅当φ∈Γ并且φ∘α1=α2∘φ. 】

4 五维幂零Hom-李代数的分类

本部分假设(g,[·,·]，α)是一个五维幂零Hom-李代数，则根据命题4(3)，知道Z(g)≠0.因此根据dim(Z(g))，五维幂零Hom-李代数至多可以分为4类：

(Ⅰ)dim(Z(g))=5(或4);

(Ⅱ)dim(Z(g))=3;

(Ⅲ)dim(Z(g))=2,

(Ⅳ)dim(Z(g))=1.

显然有下面的结论:

定理4 设dim(Z(g))=5(或4)，则五维幂零Hom-李代数(g,[·,·]，α)是交换的.设(g1,[·,·]1，α)和(g2,[·,·]2，β)是2个五维幂零Hom-李代数,且dim(Z(g1))=dim(Z(g2))=5(或4)，设A(或B)是α(或β)在g1(或g2)的任意一组基下对应的矩阵，则2个五维幂零Hom-李代数(g1,[·,·]1，α)和(g2,[·,·]2，β)同构,当且仅当A和B是相似矩阵.

证明 显然由假设条件可以得到结论. 】

定理5 设dim(Z(g))=3.

(1)对五维幂零Hom-李代数(g,[·,·]，α)，可以选择一组基{x1∈[g,g],x2,x3,x4,x5}，使得方括号运算满足[x4,x5]=x1，其余为零.

(2)设g=Cx1⊕Cx2⊕Cx3⊕Cx4⊕Cx5是一个复数域上的向量空间，定义方括号运算：[x4,x5]=x1，其余为零，则对g上的任意线性映射α，(g,[·,·]，α)是五维幂零Hom-李代数.

(3)由向量空间g，(2)中方括号运算和g上的线性映射α1和α2定义的五维幂零Hom-李代数(g,[·,·]，α1)和(g,[·,·]，α2)同构当且仅当存在φ∈Π，使得φ∘α1=α2∘φ，其中

Π={φ是g上的可逆线性映射：

证明 (1)当dim(Z(g))=3，显然可以得到dim([g,g])=1并且[g,g]⊆Z(g).因此可以选择2个非零向量x1∈[g,g],x2,x3∈Z(g)使得{x1,x2,x3}线性无关，然后将{x1,x2,x3}扩充为g的一组基{x1,x2,x3,x4,x5}使得方括号运算为[x4,x5]=x1，其余为零.

(2)对g上的任意线性映射α，显然Hom-Jacobi等式成立，因此 (g,[·,·]，α)是Hom-李代数，由方括号运算，显然g2=0，所以(g,[·,·]，α)是幂零的.

(3)由(2)，对g上的任意线性映射α1和α2，(g,[·,·]，α1)和(g,[·,·]，α2)都是五维幂零Hom-李代数.设φ是g上的可逆线性映射，容易验证对任意x,y∈g,φ([x,y])=[φ(x),φ(y)]，当且仅当

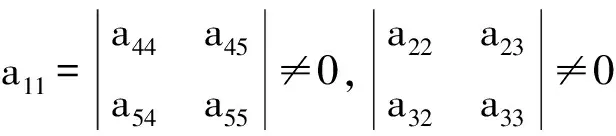
定理6 设dim(Z(g))=2.

(1)五维幂零Hom-李代数按方括号运算的形式可分为互不同构的3类:设{{x1,x2}∈Z(g),x3,x4,x5}是一组基

(a)[x3,x4]=x1,[x3,x5]=x2，其余为零;

(b)[x3,x4]=x1,[x4,x5]=x3，其余为零;

(c)[x3,x4]=x1,[x3,x5]=x2,[x4,x5]=x3，其余为零.

(2)设g=Cx1⊕Cx2⊕Cx3⊕Cx4⊕Cx5是复数域上的向量空间，定义上述(a),(b)或(c)型方括号运算.则对任意线性映射α(α∈T1或α∈T2)，(g,[·,·]，α)是一个五维幂零Hom-李代数，其中

*表示任意复数}.

*表示任意复数}.

(3)由向量空间g，(2)中(a),(b)或(c)型方括号运算以及g上的线性映射α1和α2(α1,α2∈T1，或α1,α2∈T2)定义的五维幂零Hom-李代数(g,[·,·]，α1)和(g,[·,·]，α2)同构当且仅当存在φ∈Π1(ψ∈Π2或η∈Π3)，使得φ∘α1=α2∘φ(ψ∘α1=α2∘ψ或η∘α1=α2∘η)，其中

Π1={φ是g上的可逆线性映射:

Π2={Ψ是g上的可逆线性映射:

Π3={η是g上的可逆线性映射:

证明 (1)当dim(Z(g))=2，显然dim([g,g])≤4，如果dim([g,g])=4，则g不是幂零的，与已知条件矛盾.

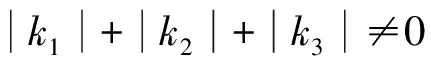
如果dim([g,g])=2，则分为2种情况，[g,g]=Z(g)和[g,g]≠Z(g).

(Ⅰ)当[g,g]=Z(g)时，可以选择g的一组基{x1,x2,x3,x4,x5}使得方括号运算满足：[x3,x4]=x1, [x3,x5]=x2，其余为零，这就是(a)型；

(Ⅱ)当[g,g]≠Z(g)，可以选择非零向量x1∈Z(g)∩[g,g]，x2∈Z(g),x3∈[g,g]使得{x1,x2,x3}线性无关，再将其扩充为g的一组基{x1,x2,x3,x4,x5}.设

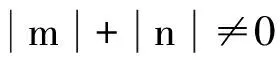
(Ⅲ)如果dim([g,g])=3，则由g的幂零性可以得到Z(g)⊆[g,g].因此可以选择g的一组基{x1∈Z(g),x2∈Z(g),x3∈[g,g],x4,x5}使得方括号运算为[x3,x4]=x1, [x3,x5]=x2, [x4,x5]=x3，其余为零，这就是(c)型.

(2)对(a)型，显然Hom-Jacobi等式对g上的任意线性映射α都成立，而且由方括号运算得g3=0，所以(g,[·,·],α)是一个五维幂零Hom-李代数.

对(b)型，设α是g上的一个线性映射，则只要证明α对{x1,x4,x5}，{x2,x4,x5},{x3,x4,x5}满足Hom-Jacobi等式即可，即

由方括号运算，上面的算式可以化简为

因此，

则α满足Hom-Jacobi等式当且仅当α∈T1，故推出(g,[·,·],α1)是Hom-李代数，由于g3=0，所以g是幂零的.

(c)型的证明与(b)型类似，我们在此省略.

(3)对(a)型，由(2)，对g上的任意线性映射α1和α2，(g,[·,·],α1)和(g,[·,·],α2)都是五维幂零Hom-李代数.设φ是g上的可逆线性映射，容易验证对任意x,y∈g,φ[x,y]=[φ(x),φ(y)]当且仅当

其中:

因此φ是(g,[·,·],α1)到(g,[·,·],α2)的同构当且仅当φ∈Π1,并且φ∘α1=α2∘φ.

类似于(a)型的证明，我们很容易验证(b)型和(c)型，因此(b)型和(c)型的证明省略. 】

注：当dim(Z(g))=1时，五维幂零Hom-李代数的分类更加复杂，对这种类型以及更一般的n维幂零Hom-李代数的分类，我们将在以后的论文中给出.

[1]HARTWIGJT,LARSSOND,SILVESTROVSD.DeformationsofLiealgebrasusing-derivations[J].J Algebra,2006,295:314.

[2] BENAYADI S, MAKHLOUF A.Hom-Lie algebras with symmetric invariant nondegenerate bilinear forms[J].JofGeometryandPhys,2014,76:38.

[3] SHENG Y H. Representations of Hom-Lie algebras[J].AlgebraRepresentTheory,2012,15(6):1081.

[4] MAKHLOUF A,SILVESTROV S.Notes on formal deformations of Hom-associative and Hom-Lie algebras[J].ForumMath,2010,22(4):715.

[5] YAU D.Hom-Yang-Baxter equation,Hom-Lie algebras,and quasi-triangular bialgebras[J].JPhysA:MathTheor,2009,42(16):1076.

[6] YAU D.Hom-algebras and homology[J].JLieTheory,2009,19(2):409.

[7] YAU D.Enveloping algebras of Hom-Lie algebras[J].JGenLieTheoryAppl,2008,2:95.

[8] JIN Q Q,LI X C. Hom-Lie algebra structures on semi-simple Lie algebras[J].JAlgebra,2008,319(4):1398.

[9] MAKHLOUF A,SILVESTROV S. Hom-algebra structures[J].JGenLieTheoryAppl,2008,2(2):51.

(责任编辑 陆泉芳)

Classification of finite-dimensional nilpotent Hom-Lie algebras

CHEN Xue1,HAN Wei2

(1.School of Applied Mathematics,Xiamen University of Technology,Xiamen 361024,Fujian,China；2.School of Mathematical Sciences,Shanghai Jiaotong University,Shanghai 200240,China)

Some properties on nilpotent and solvable Hom-Lie algebras are presented in this paper.The results on solvability and nilpotency of classical finite dimensional Lie algebras are generalized to Hom-Lie algebras.Furthermore,four dimensional and five dimensional nilpotent Hom-Lie algebras are classified.By the dimension of the half center of Hom-Lie algebras,four dimensional and five dimensional nilpotent Hom-Lie algebras can be divided into three and four different classes.

Hom-Lie algebra;nilpotency;classification

10.16783/j.cnki.nwnuz.2016.06.002

2016-05-10;修改稿收到日期:2016-09-06

国家自然科学基金资助项目(11426191)；厦门理工学院高层次人才引进项目(YKJ13028R)

陈雪(1984—),女，安徽六安人，讲师，博士.主要研究方向为李代数及其表示理论.

E-mail:xuechen@xmut.edu.cn

O 152.5

A

1001-988Ⅹ(2016)06-0006-07