高超声速飞行器热环境与结构传热的多场耦合数值研究

周印佳，孟松鹤＊，解维华，杨强

哈尔滨工业大学 复合材料与结构研究所，哈尔滨 150080

高超声速飞行器热环境与结构传热的多场耦合数值研究

周印佳，孟松鹤＊，解维华，杨强

哈尔滨工业大学 复合材料与结构研究所，哈尔滨 150080

为了准确预测高超声速飞行器面临的严峻气动热／力环境以及结构的热力响应，发展了高超声速流动与结构传热耦合框架。采用分区求解方法，通过耦合界面的实时数据传递，实现了基于Navier－Stokes方程的高超声速化学非平衡计算流体力学（CFD）求解器与结构的热力全耦合有限元法（FEM）求解器的多场耦合计算，建立了高超声速飞行器的多场耦合数值分析方法。首先对经典高超声速圆柱绕流实验进行了耦合计算，结果与实验值吻合良好。然后针对典型的超高温陶瓷（UHTC）材料的耦合传热问题进行了数值研究，考虑热传导效应对气动热环境和结构热响应预测的影响，结果表明对于复杂外形且热导率相对较高的UHTC材料，结构内部热传导对热环境和表面温度分布的影响不可忽略。最后针对UHTC材料热物性（比热和热导率）非线性对高超声速流动传热过程的影响进行了研究，结果表明当比热和热导率处于合理的误差范围内时，材料表面温度响应对其变化并不敏感。

高超声速飞行器；多场耦合；气动热；数值模拟；热防护

高超声速飞行器的快速发展给热防护设计带来了更为严峻的挑战［1］。准确地预测气动热／力环境、结构温度和应力状态，能够在提高飞行器安全性能的同时减小热防护系统设计冗余，对提高飞行器的性能有着极为重要的意义。

传统的高超声速飞行器的热／力载荷环境的预测与热防护结构性能的分析基本还处于分离状态。这种方法实际上把多场耦合的事实人为地分割成多个独立的物理场。在这种情况下，既无法得到精确的气动热／力载荷环境，也无法正确评价热防护材料及其结构的服役特征。

高超声速飞行热防护设计是一个涉及到真实气体效应、耦合传热和结构热力响应的复杂的多场耦合问题，必须采用多场耦合的方法求解。国外较早开展了多场耦合方法的研究，并在1987年首次发表了关于多场耦合分析研究方面的成果。Wieting等［2－3］做了高超声速圆柱绕流试验，此后经常被用于高超声速流动－传热耦合数值模拟的验证。Thornton等［4－5］采用流－热－固一体化有限元法（FEM）研究了飞行器面板以及前缘的气动热－结构相互作用，得到了与实验相符的冷壁热流。Loehner等［6］通过在每个时间步对耦合界面处的变量进行插值，成功地将已有的计算流体力学（CFD）、计算热力学和计算结构动力学程序耦合在一起。近期的研究有，Miller等［7］发展了多物理场时间推进的流动－传热－结构分区松耦合方法。该方法充分利用了流－热－结构的时间尺度差异，在每个传热分析时间步内有多个结构分析时间步，每个结构时间步内有多个流动时间步，兼顾了计算精度和效率。

21世纪初，国内学者首先对流场、热、结构一体化数值模拟方法展开研究。黄唐［8］和夏刚［9］等开展了二维流动－传热耦合模拟，二者的研究中固体传热均采用FEM，流体则分别采用有限差分法和有限体积法。桂业伟［10］、耿湘人［11］、Zhao［12］和张兵［13］等相继开展了流场、热、结构多场耦合计算研究和分析。国内学者最近的研究有，Zhang等［14］开发了预测高超声速气动热环境的流动－传热－结构一体化分析方法，采用松耦合方法耦合了稳态的CFD求解器与瞬态热结构力学求解器。董维中等［15］基于流场的非平衡Navier－Stokes方程、表面的能量守恒方程和内部的热传导方程建立了表面温度分布与气动热的耦合计算方法，并考虑了流场的非平衡效应、表面的热辐射效应、催化效应和烧蚀效应以及热防护层内部的热传导效应。

由于多场耦合问题的复杂性，还需要进一步开展分析方法研究，深刻把握防热系统多场耦合规律及其效应。需要指出的是，高超声速飞行器面临严峻的气动热环境，材料在高温下的热物性（热导率和比热）非线性对耦合传热过程的影响目前尚未见到相关研究。

本文发展了高超声速流动和结构传热的耦合框架，实现了高超声速非平衡流动求解器与结构热力全耦合的多场耦合计算，建立了高超声速飞行器的多场耦合数值分析方法。考虑热传导效应对气动热环境和结构热响应预测的影响，并针对材料的比热和热导率非线性对高超声速流动传热过程的影响进行了研究。

1 耦合分析模型与耦合策略

本文的耦合分析模型如图1所示。在该模型中，流场采用同时求解连续、动量、能量等守恒方程的耦合解格式得到热流qw和压力pw，结构场采用热力全耦合的方法进行求解得到壁面温度Tw和结构位移us。这两个独立的模型通过在流－固耦合界面上实时交换参数来表征外部高超声速流动与内部结构响应和热响应的耦合作用。热流和压力的联合载荷影响结构的热力行为，相应的壁面温度和位移影响外部流场的气动热力学行为。

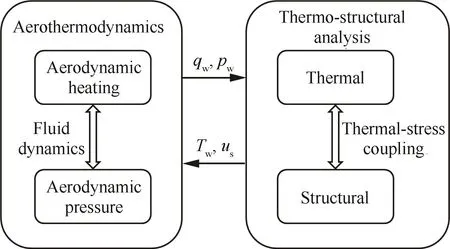
图1 多场耦合分析模型Fig．1 Multi－field coupling analysis model

采用分区求解方法完成对高超声速流动与结构传热的耦合分析。流体和固体区域的求解器均为瞬态求解，每个求解器所需要的下一步计算的数据在耦合界面上反复交换。图2中给出了耦合策略示意图，详细描述如下：

1）在等温壁面边界条件下（结构温度确定的定常壁温）进行稳态流动计算，结果作为瞬态耦合分析的初始条件。在耦合起始点，进行瞬态流动计算，得到初始时刻热流qw和壁面压力pw。

2）qw和pw在流体－固体耦合界面进行插值，作为结构求解器的边界条件，在热流和压力联合载荷下进行热－结构耦合分析。一个时间步Δt后，结构求解器得出壁面温度Tw和结构位移us。

3）us通过界面插值进行传递，更新流场网格，Tw更新流体求解的壁面温度边界条件，进行下一步流场计算。经过一个时间步Δt后得到新的qw和pw，提取出来用于下一时间步的结构计算。

该过程不断重复直到计算时间结束。

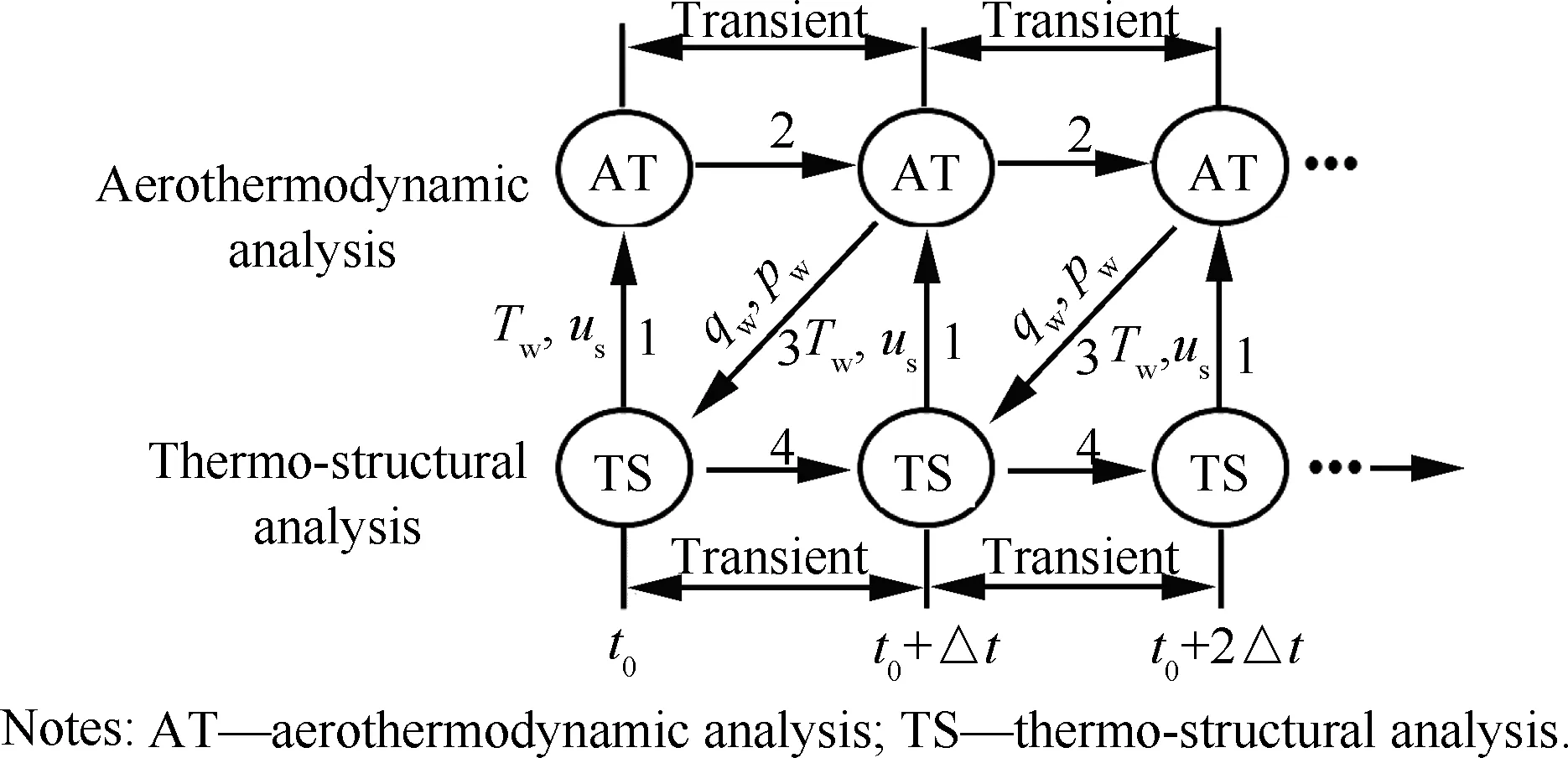
图2 本文所用耦合策略Fig．2 Coupling strategy in this paper

2 非平衡流场计算

2．1 流动方程

文中考虑高超声速飞行器周围的流场为化学非平衡、热力学平衡的黏性可压缩连续流动，连续、动量、能量守恒方程分别为对于包含组分混合或反应的流动，还需要组

分守恒方程，即

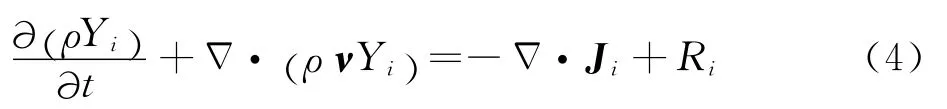
式（1）～式（4）中：p和ρ分别为混合气体的压力和密度；ν为速度向量；τ为应力张量；E为比总能量；λ为气体热导率；h为焓；Ji为组分i的质量扩散通量；Yi为组分i的质量分数；Ri为组分i的净生产率。

组分的分压由组分密度和混合气体的温度求得，混合气体的压力由Dalton定律［16］给出。

2．2 化学动力学模型

由于存在动能耗散和激波，高超声速飞行器周围的空气会达到极高的温度，高温使气体离解甚至电离。化学非平衡假设即特征化学反应时间与流动的特征时间相当。采用Park和Lee［17］的5组分（O，N，NO，O2，N2）17反应化学动力学模型，并考虑第三体效应。如表1所示，反应机制包括3个分解反应和2个交换反应。Park动力学模型中的常数Ar、βr和Er在表1中给出。

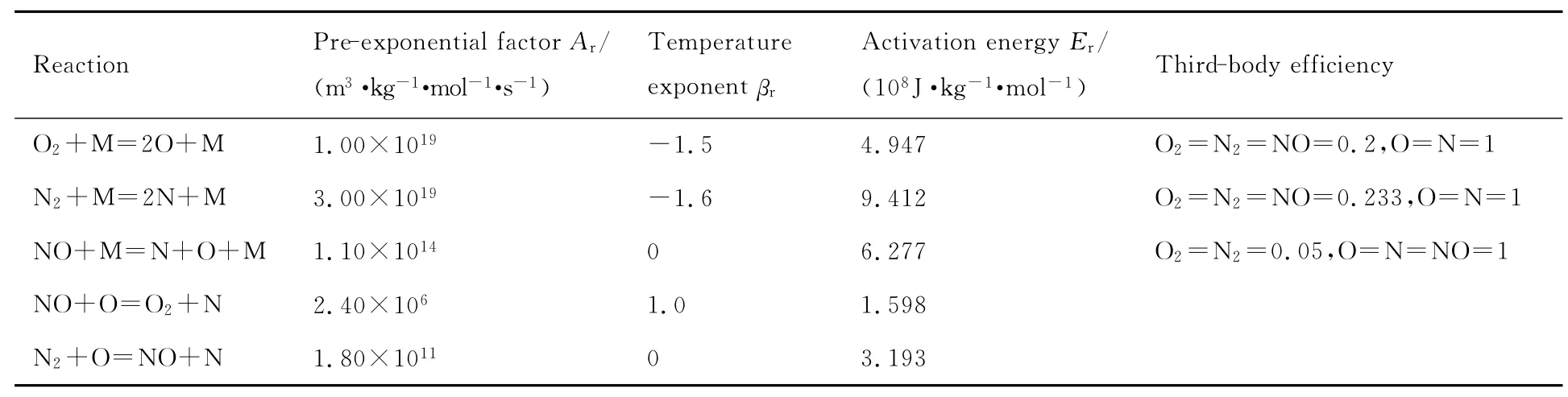
表1 Park 5组分动力学模型及反应速率参数Table 1 Reaction－rate parameters based on Park’s 5－species kinetic model

2．3 输运属性

单一组分的黏性系数μi、热导率λi和扩散系数Dij由气体分子动力论［18］计算得到。

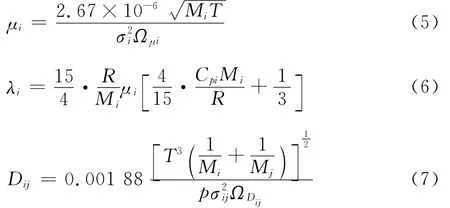
式中：R为普适气体常数；Cpi为组分i的比热；Mi为组分i的分子量；σij＝（σi＋σj）／2，σi为组分i的特征分子直径；Ω为碰撞积分。

混合气体的系数可以由半经验Wilke公式［19］给出，即

式中：Xi为组分i的摩尔分数。

混合气体的多组分扩散系数由式（11）的近似表达式计算。

2．4 热力学模型

有限速率化学反应流动的计算需要每种单一组分的热力学属性（比热Cpi和焓hi）。本文中只考虑流动为化学非平衡、热力学平衡状态的反应气体，每种组分的热力学属性由当地静温计算。高温气体的Cpi和hi可以通过温度的多项式曲线拟合函数［20］计算：

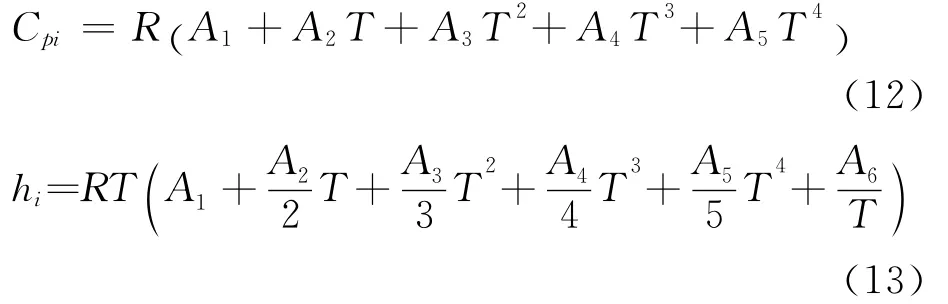
式中：Ai（i＝1～6）为拟合系数。

混合气体的属性可由单一组分的属性确定：

式中：NS为组分数量。

2．5 数值方法

对于高超声速化学非平衡流动计算，连续、动量、能量和组分方程采用有限体积法同时求解。已有研究［21］表明，不同数值格式对热流计算精度有较大影响。通过大量数值结果与实验数据对比，表明AUSM＋格式在热流计算精确性方面具有优势。因此，本文计算采用AUSM＋格式。

3 热－结构控制方程

3．1 热传导

基于能量守恒定律和Fourier定律，可以得到结构瞬态热传导方程

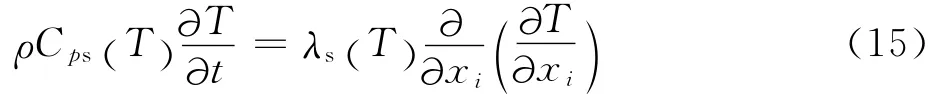
式中：λs为固体热导率；Cps为固体比热容。

3．2 结构响应

当固体结构受到加热时，它的体内温度会发生变化，这时在结构内部会有温差存在。由于热膨胀以及结构的约束作用，固体结构产生热应力，热应力又导致了热变形的发生。对于二维结构的响应方程为

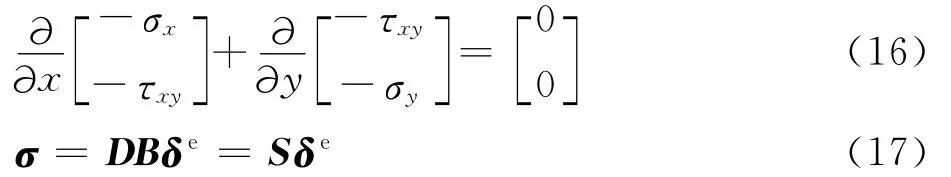
式中：σx、σy和τxy为固体结构的应力分量；而D为弹性矩阵；B和S分别为应变和应力矩阵；δe为位移矩阵。

在本文计算中，暂不考虑模量和泊松比等弹性参数随温度的变化。

固体区域内，采用有限元法进行热－结构分析。在本文研究中，应力分析与温度分布相关，而温度分布对应力为弱相关。但是在当前工作中，仍然考虑应力与温度分布之间的双向耦合关系，进行了热力全耦合分析。温度用向后差分格式积分，非线性耦合系统采用牛顿法求解。牛顿迭代法采用非对称雅克比矩阵，描述为如式（18）所示的矩阵方程组。

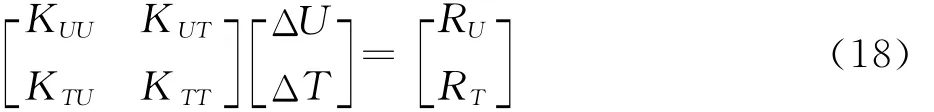
式中：ΔU和ΔT分别为修正后的位移和温度增量；Kij（i，j＝U，T）为完全耦合雅克比矩阵的子阵；RU和RT分别为计算结构力与热的残差。采用这种方式求解方程组，热力与结构问题是同时求解的。

4 耦合框架验证

为了验证耦合策略和数值方法，选择了经典的圆柱绕流实验作为算例。实验来流马赫数、压力和温度分别为6．47、648Pa和241．5K，不锈钢管长度、直径和厚度分别为0．609 6m、0．076 2m和0．012 7m。计算中采用标准钢材的热力学参数，其中：热导率为16．27W／（m·K），比热为502．48J／（kg·K），密度为8 030kg／m3，弹性模量为1．2×1013Pa，热膨胀系数为1．68×10－51／K，泊松比为0．3。实验的更多细节由文献［3］给出。

流体区域为结构网格，固体区域采用四边形单元，二者在耦合界面处不匹配。边界层网格进行加密以保证计算结果的网格无关性，并使其具有足够的分辨率。流场和圆柱的计算模型如图3所示。计算中采用了SST k－ω 湍流模型。

图4给出了不同耦合时间步长时驻点处的温度随时间变化曲线，图5为驻点热流变化趋势。可以看出，随着加热时间增长，驻点温度逐渐升高，而热流变化趋势则相反。另外，温度和热流都在初始的一小段时间内变化剧烈，而后变化趋于缓和。基于不同耦合时间步长得到了不同的温度分布结果，其中Δt＝0．000 1s时得到t＝2s时的

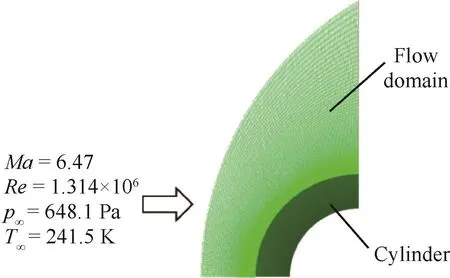
图3 圆柱绕流计算模型Fig．3 Calculation model for flow over a cylinder

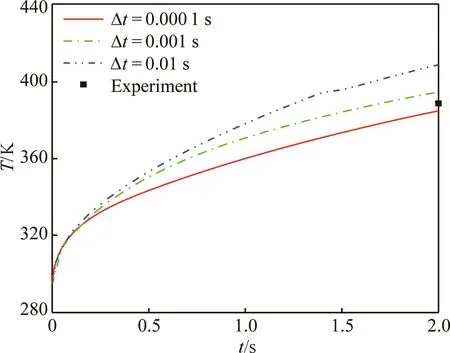
图4 驻点温度随时间变化曲线Fig．4 Time histories of stagnation point temperature

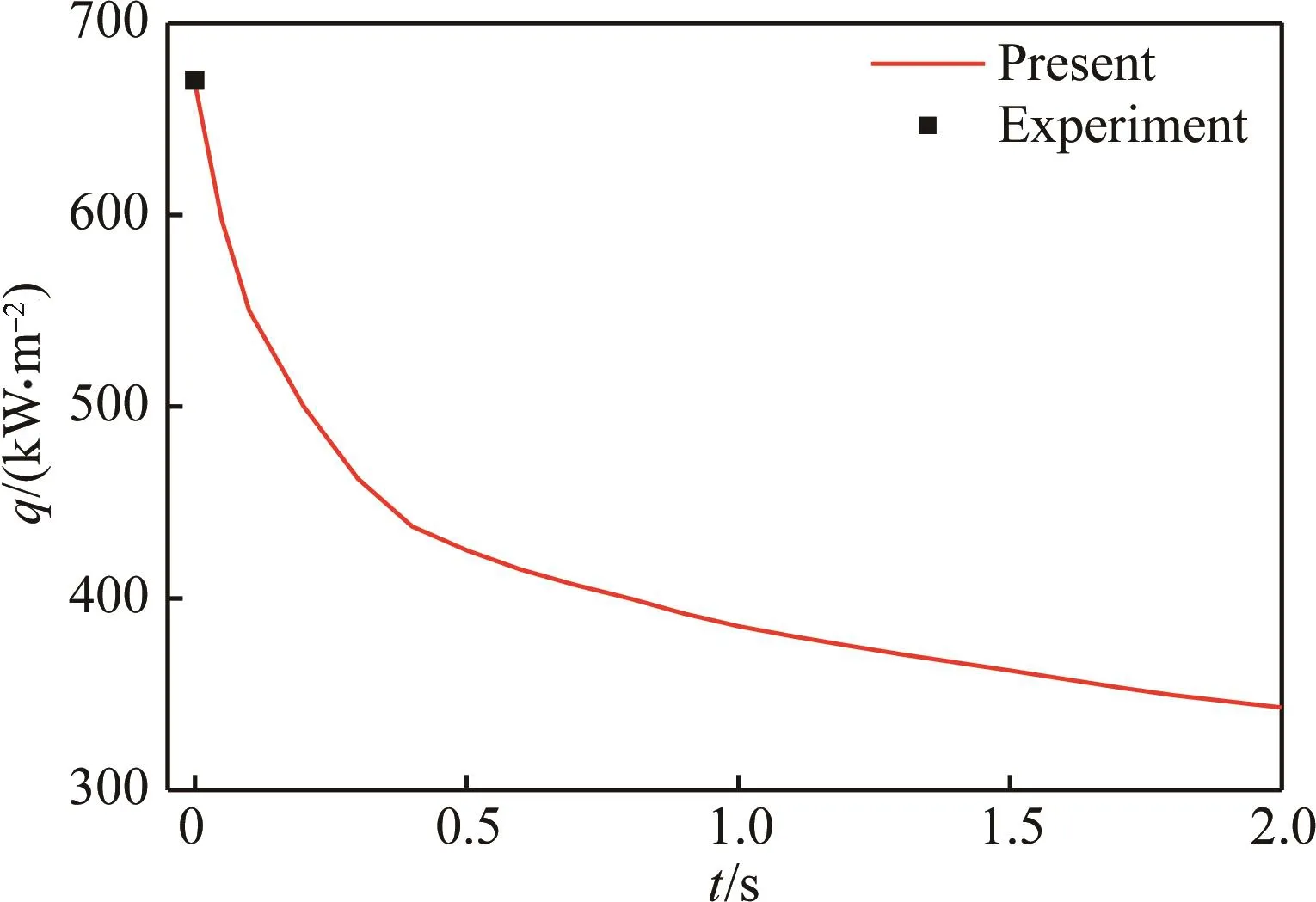
图5 驻点热流随时间变化曲线Fig．5 Time histories of stagnation point heat flux

结果（384．9K）与实验结果（约为388．72K）最为接近，而对于Δt＝0．001s和Δt＝0．01s，得到了略偏高的温度结果。可以得出结论，随着时间步长偏离某个合适的特定值逐渐增大，预测的结构温度相应会逐渐偏高。以下取Δt＝0．000 1s的结果进行分析。

图6和图7给出了不同时间点的温度和热流分布。在气动加热开始后的前0．5s内，温度和热流变化比较明显。

图8显示，在热力联合载荷下，驻点处的位移和Mises应力都随时间逐渐增大，但是在当前工况下位移量较小，不足以明显影响流场。图9给出了流体域中心线上的压力和温度分布，所预测的激波后温度和压力与实验值非常吻合。

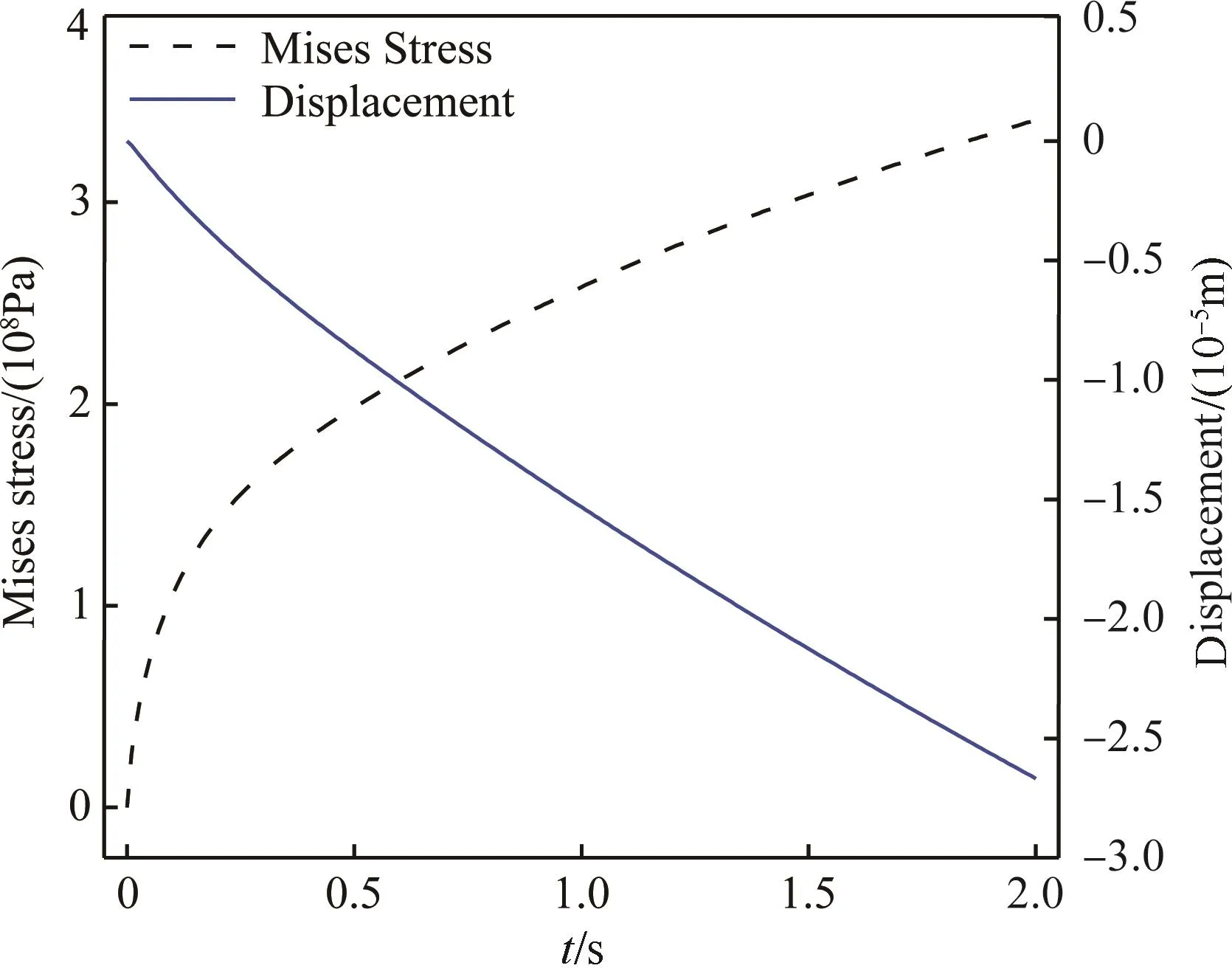
图8 结构Mises应力和位移Fig．8 Mises stress and displacement

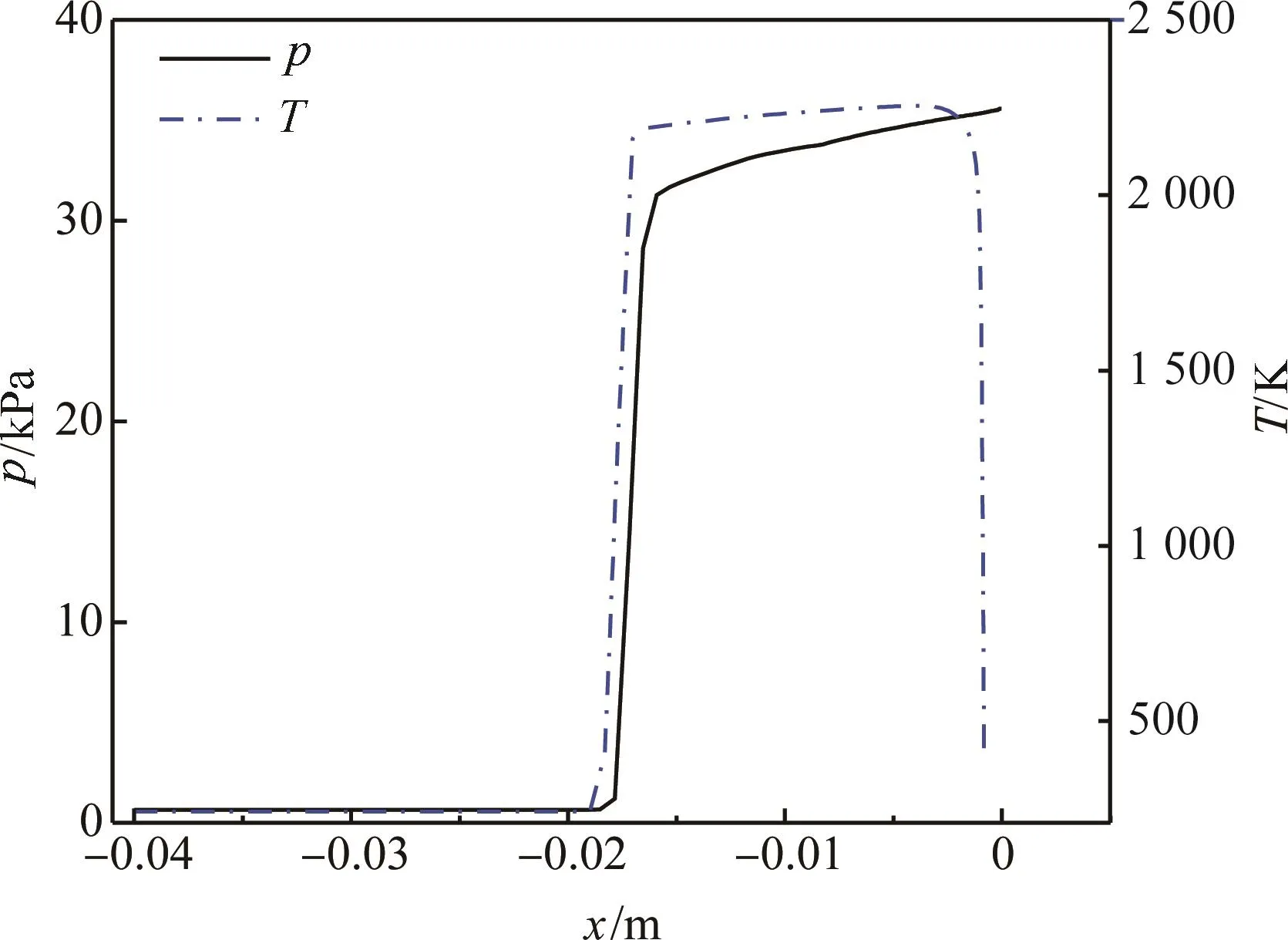
图9 驻点线温度和压力分布Fig．9 Fluid temperature and pressure distributions along stagnation line

5 材料热物性对耦合传热的影响

本算例主要分析超高温陶瓷（UHTC）双锥的耦合传热问题，计算对象为德国L2K高温风洞中的轴对称UHTC双锥。双锥几何尺寸如图10

图10 双锥几何示意图Fig．10 Schematic of double cone geometry

所示，后部有铜质夹具支撑。来流马赫数、压力和温度分别为4．57，272Pa和764K，混合气体中N2、O2和O组分的质量分数分别为0．739、0．113和0．092。材料表面为完全催化壁面，其辐射率为0．85。更多试验细节和计算结果见文献［22］和文献［23］。

为了能够精确地预测结构的热流和温度分布，采用了温度相关的材料热物性［24］，如图11所示。本次计算采用ZrB2－30vol．%SiC的材料物性，其余参数用于后面对比分析热物性对传热影响的研究。计算过程中的流动为层流状态。

由前面的算例可知，耦合时间步长Δt＝0．001s可以得到比较准确的结果并具有较高的效率，因此计算采用耦合时间步长Δt＝0．001s，计算时间总长为90s。壁面设为完全催化壁面，即所有原子均在壁面发生复合，则壁面处的组分浓度与来流组分相同，即（Yi）w＝Yi，∞。

图12给出的是本文方法计算的距离前缘4mm和35mm处的壁面温度，与文献［12］中的数值结果及实验测得结果的对比。在x＝4mm处，本文计算所得壁面温度结果低于实验值。在t＜40s时计算结果与实验值比较接近，但是在t＞40s时，与实验值偏差逐渐加大，直到t＝90s时最大相差约91K。而在x＝35mm处，本文结果与实验值和文献值［22］都吻合得较好。造成头部最终温度偏低的原因可能与采用热力平衡模型有关。

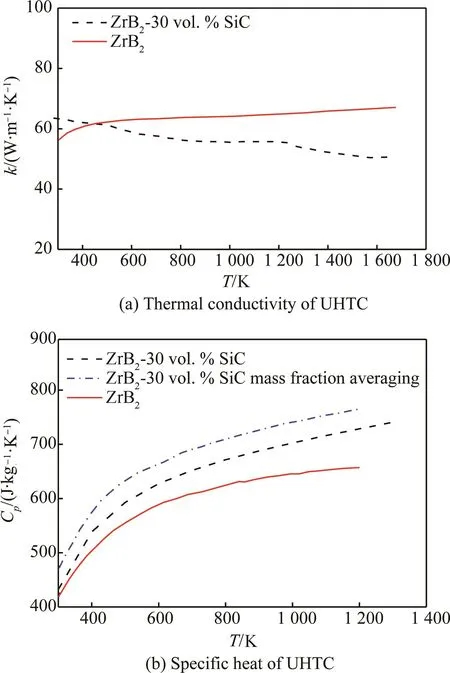
图11 超高温陶瓷（UHTC）材料随温度变化的热物性Fig．11 Temperature dependent thermophysical properties of ultra high temperature ceramics（UHTC）

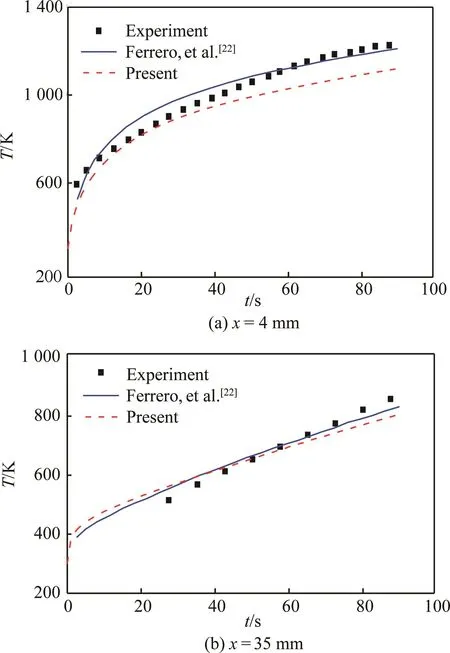
图12 壁面温度随时间变化曲线Fig．12 Time histories of wall temperature

传统的热防护系统一般是良好的隔热体，热导率较小，并能够有效地辐射热量。因此计算热载荷与表面温度时通常忽略固体内部热传导，对流传热与向外辐射热之间形成局部热平衡。此时计算得到的局部辐射平衡壁面温度能够满足工程需求。而对于如UHTC这类热导率较高的新型防热材料，表面对流加热一部分向固体内部传导，另一部分辐射回大气。当系统达到稳态时，形成全局辐射热平衡。因此，对于超高温陶瓷类前缘结构，局部热辐射平衡被打破，需要考虑结构内部热传导。

图13给出了是否考虑热传导情况下表面温度分布和热流对比。可以看到，考虑热传导以后，双锥的头部和肩部的大量热量传导到温度较低的中间部分和尾部，从而使头部和肩部的温度显著降低，其中驻点处温度比辐射平衡状态的温度降低了500K左右。由于头部和肩部温度变化幅度较大，因此导致其热流增大明显；而热流相对较小的中部和尾部，表面热流由于温度升高而略有降低。因此，对于外部环境变化剧烈或者热导率较高且外形复杂的结构，结构内部热传导对热环境和表面温度分布的影响不可忽略。

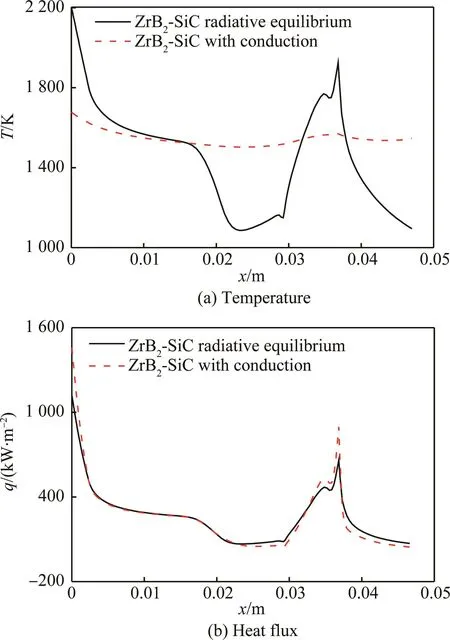
图13 有无热传导情况下双锥表面温度和热流分布对比Fig．13 Comparison of surface temperature and surface heat flux distribution with and without heat conduction

在高超声速流动引起的严峻气动热环境中，材料热物性非线性会对传热过程产生显著影响。目前对于该问题研究的相关报道还不多见。下面主要针对材料热导率、比热容等热物性的非线性对高超声速流动传热过程的影响进行了研究。

共进 行 4 组计 算，分 别 为：①ZrB2－SiC，Cp（T）和k（T）均采用ZrB2－30vol．%SiC的物性，作为基础物性和参照对象；②ZrB2，Cp（T）和k（T）均采用ZrB2的物性，考察热导率和比热物性同时作用的影响；③ZrB2－SiC＿Cp，k（T）取基础物性，Cp（T）采用 ZrB2－30vol．%SiC的质量分数平均计算得到的比热值，考察比热在合理的物性偏差内的影响；④ZrB2－SiC＿k，Cp（T）取基础物性，k（T）采用ZrB2的物性，考察热导率对传热的影响。计算所用的各物性参数如图11所示。

图14给出的是以上不同物性参数情况下计算的表面温度对比。可以看出在初始的一段时间内物性参数的变化对热响应的影响甚微，基本可以忽略不计，差别在一定时间后即结构达到一定温度（大于800K）时开始显现。整体上看，在90s时间内热导率和比热对材料表面最终温度的影响有限。

通过曲线ZrB2－SiC与曲线 ZrB2－SiC＿k的对比可以看出，较高的热导率使头部热量得以向低温区转移，使其温度降低了约40K，变化量为3．6%；而在温度较低的肩部，各组计算结果差异很小，热导率造成的差异仅为8K，降低了1%。

通过曲 线 ZrB2－SiC 与曲线 ZrB2－SiC＿Cp的对比可以看出，使用质量分数平均比热值计算的表面温度低于对照值。这是因为由质量分数平均预测的比热值高于作为基础物性的ZrB2－30vol．%SiC实际测量值，因此每升高一度所需要的能量更多，因此在同样来流条件下，高比热容能够降低材料表面的温度。但是从结果可以看出，材料表面温度对合理范围内的比热值变化并不敏感，在超出比热测量误差±3%范围、比热值平均相差50J／（kg·K）的情况下，造成的温度差异在头部最大为11K，偏差为0．98%，肩部仅为11．3 K，偏差为1．4%。

图14 不同热物性参数作用时的表面温度分布对比Fig．14 Comparison of surface temperature distribution for different thermophysical properties

最后，曲线ZrB2－SiC与曲线ZrB2的对比显示，ZrB2的热导率高于ZrB2－SiC，使其头部温度有低于ZrB2－SiC的趋势，而ZrB2的比热低于ZrB2－SiC，有使其温度高于ZrB2－SiC的趋势。二者共同作用，其表面温度介于比热和热导率单独作用的曲线之间。

6 结 论

1）传统的先流场再结构的耦合方法无法得到精确的气动热力载荷环境，也无法正确评价热防护材料及其结构的服役特征。采用高超声速流动和结构传热耦合的方法，对高超声速飞行器的气动热力环境和结构热力响应的预测更符合物理实际，保证计算精度。

2）对于如超高温陶瓷（UHTC）这类热导率较高的新型防热材料，必须考虑热传导效应对气动热环境和结构热响应预测的影响。考虑热传导效应后表面温度和热流相差分别可达500K和330kW／m2。

3）对UHTC类材料热物性非线性对高超声速流动传热过程的影响进行了研究，结果表明比热和热导率在合理误差范围内的变化对材料表面温度响应的影响有限。在比热变化±3%范围、比热值平均相差50J／（kg·K）的情况下，造成的温度差异最大仅为0．98%

［1］ 彭治雨，石义雷，龚红明，等．高超声速气动热预测技术及发展趋势［J］．航空学报，2015，36（1）：325－345．PENG Z Y，SHI Y L，GONG H M，et al．Hypersonic aeroheating prediction technique and its trend of development［J］．Acta Aeronautica et Astronautica Sinica，2015，36（1）：325－345（in Chinese）．

［2］ WIETING A R．Experimental study of shock wave interference heating on a cylindrical leading edge：NASA－TM－100484［R］．Washington，D．C．：NASA，1987．

［3］ WIETING A R，HOLDEN M S．Experimental study of shock wave interference heating on a cylindrical leading edge at Mach 6and 8：AIAA－1987－1511［R］．Reston：AIAA，1987．

［4］ THORNTON E A，DECHAUMPHAI P．Finite element prediction of aerothermal－structural interaction of aerodynamically heated panels：AIAA－1987－1610［R］．Reston：AIAA，1987．

［5］ DECHAUMPHAI P，THORNTON E A，WIETING A R．Flow－thermal－structural study of aerodynamically heated leading edges［J］．Journal of Spacecraft and Rockets，1989，26（4）：201－209．

［6］ LOEHNER R，YANG C，CEBRAL J，et al．Fluid－structure－thermal interaction using a loose coupling algorithm and adaptive unstructured grids：AIAA－1998－2419［R］．Reston：AIAA，1998．

［7］ MILLER B A，CROWELL A R，MCNAMARA J J．Loosely coupled time－marching of fluid－thermal－structural interactions： AIAA－2013－1666［R］． Reston： AIAA，1998．

［8］ 黄唐，毛国良，姜贵庆，等．二维流场、热、结构一体化数值模拟［J］．空气动力学学报，2000，18（1）：115－119．HUANG T，MAO G L，JIANG G Q，et al．Two dimensional coupled flow－thermal structural numerical simulation［J］．Acta Aerodynamica Sinica，2000，18（1）：115－119（in Chinese）．

［9］ 夏刚，刘新建，程文科，等．钝体高超声速气动加热与结构热传递耦合的数值计算［J］．国防科技大学学报，2003，25（1）：35－39．XIA G，LIU X J，CHENG W K，et al．Numerical simulation of coupled aeroheating and solid heat penetration for a hypersonic blunt body［J］．Journal of National University of Defense Technology，2003，25（1）：35－39（in Chinese）．

［10］ 桂业伟，袁湘江．类前缘防热层流场与热响应耦合计算研究［J］．工程热物理学报，2002，23（6）：733－735．GUI Y W，YUAN X J．Numerical simulation on the coupling phenomena of aerodynamic heating with thermal response in the region of the leading edge［J］．Journal of Engineering Thermophysics，2002，23（6）：733－735（in Chinese）．

［11］ 耿湘人，张涵信，沈清，等．高速飞行器流场和固体结构温度场一体化计算新方法的初步研究［J］．空气动力学学报，2002，20（4）：422－427．GENG X R，ZHANG H X，SHEN Q，et al．Study on an integrated algorithm for the flowfields of high speed vehicles and the heat transfer in solid structures［J］．Acta Aerodynamica Sinica，2002，20（4）：422－427 （in Chinese）．

［12］ ZHAO X L，SUN Z X，TANG L S，et al．Coupled flowthermal－structural analysis of hypersonic aerodynamically heated cylindrical leading edge［J］．Engineering Applications of Computational Fluid Mechanics，2011，5（2）：170－179．

［13］ 张兵，韩景龙．多场耦合计算平台与高超声速热防护结构传热问题研究［J］．航空学报，2011，32（3）：400－409．ZHANG B，HAN J L．Multi－field coupled computing platform and thermal transfer of hypersonic thermal protection structures［J］．Acta Aeronautica et Astronautica Sinica，2011，32（3）：400－409（in Chinese）．

［14］ ZHANG S T，CHEN F，LIU H．Integrated fluid－thermal－structural analysis for predicting aerothermal environment of hypersonic vehicles：AIAA－2014－1394［R］．Reston：AIAA，2014．

［15］ 董维中，高铁锁，丁明松，等．高超声速飞行器表面温度分布与气动热耦合数值研究［J］．航空学报，2015，36（1）：311－324．DONG W Z，GAO T S，DING M S，et al．Numerical study of coupled surface temperature distribution and aerodynamic heat for hypersonic vehicles［J］．Acta Aeronautica et Astronautica Sinica，2015，36（1）：311－324（in Chinese）．

［16］ SILBERBERG M．Chemistry：The molecular nature of matter and change［M］．New York：McGraw－Hill，2009．

［17］ PARK C，LEE S H．Validation of multi－temperature nozzle flow code NOZNT：AIAA－1993－2862［R］．Reston：AIAA，1993．

［18］ FRANCESE A．Numerical and experimental study of UHTC materials for atmospheric re－entry［D］．Napoli：University of Napoli，2007：94－95．

［19］ ANDERSON J D．Hypersonic and high temperature gas dynamics［M］．New York：McGraw－Hill，2006：697－699．

［20］ GUPTA R N，YOS M，THOMPSON R A．A review of reaction rates and thermodynamic and transport properties for the 11－species air model for chemical and thermal nonequilibrium calculations to 30000K：NASA TM－101528［R］．Washington，D．C．：NASA，1989：13－14．

［21］ 阎超，禹建军，李君哲．热流CFD计算中格式和网格效应若干问题研究［J］．空气动力学报，2006，24（1）：125－130．YAN C，YU J J，LI J Z．Scheme effect and grid dependency in CFD computations of heat transfer［J］．Acta Aerodynamica Sinica，2006，24（1）：125－130（in Chinese）．

［22］ FERRERO P，D’AMBROSIO D．A numerical method for conjugate heat transfer problems in hypersonic flows：AIAA－2008－4247［R］．Reston：AIAA，2008．

［23］ MURTY M C，MANNA P，CHAKRABORTY D．Conjugate heat transfer analysis in high speed flows［J］．Proceedings of the Institution of Mechanical Engineers，Part G：Journal of Aerospace Engineering，2013，227（10）：1672－1681．

［24］ ZIMMERMANN J W．Thermophysical properties of ZrB2and ZrB2－SiC ceramics［J］．Journal of the American Ceramic Society，2008，91（5）：1551－2916．

Multi－field coupling numerical analysis of aerothermal environment and structural heat transfer of hypersonic vehicles

ZHOU Yinjia，MENG Songhe＊，XIE Weihua，YANG Qiang
Center for Composite Materials，Harbin Institute of Technology，Harbin 150080，China

A coupling framework of hypersonic flow，heat transfer and structural response is presented in this paper in order to accurately predict aerodynamic environment，extreme aerothermal environment，as well as thermal and structural response for hypersonic flight．Multi－field coupling analysis is implemented in conjunction with the hypersonic chemical nonequilibrium computational fluid dynamics（CFD）solver and the fully coupled thermo－structural finite element method（FEM）solver by using partition algorithm，with a real time data exchange between non－matched meshes．This coupling method is validated by comparison with the experiment of a turbulent flow over a circular cylinder and good agreements with experiment are achieved．Coupling analysis of ultra high temperature ceramics（UHTC）is also conducted，and the effects of thermal conductivity on the prediction of aerothermal environment and structural thermal response have been considered．The results show that the effects of structural internal heat conduction on aerothermal environment and surface temperature distribution cannot be neglected for a structure with high thermal conductivity and complex geometry．At last，the effects of non－linear thermophysical properties（specific heat and thermal conductivity）of UHTC on hypersonic flow and heat transfer process have been studied．The results show that the surface temperature of structure is not sensitive to thermal conductivity and specific heat when thermal conductivity and specific heat are in a limit of allowable error．

hypersonic vehicles；multi－field coupling；aeroheating；numerical simulation；thermal protection

2015－09－08；Revised：2015－11－22；Accepted：2016－02－15；Published online：2016－02－23 09：00

URL：www．cnki．net／kcms／detail／11．1929．V．20160223．0900．008．html

s：National Natural Science Foundation of China（11272107）；National Basic Research Program of China（2015CB655200）

V434＋．11

A

1000－6893（2016）09－2739－10

10．7527／S1000－6893．2016．0040

2015－09－08；退修日期：2015－11－22；录用日期：2016－02－15；网络出版时间：2016－02－23 09：00

www．cnki．net／kcms／detail／11．1929．V．20160223．0900．008．html

国家自然科学基金（11272107）；国家“973”计划（2015CB655200）

＊通讯作者．Tel．：0451－86417560 E－mail：mengsh＠hit．edu．cn

周印佳，孟松鹤，解维华，等．高超声速飞行器热环境与结构传热的多场耦合数值研究［J］．航空学报，2016，37（9）：2739－2748．ZHOU Y J，MENG S H，XIE W H，et al．Multif－ield coupling numerical analysis of aerothermal environment and structural heat transfer of hypersonic vehicles［J］．Acta Aeronautica et Astronautica Sinica，2016，37（9）：27392－748．

周印佳 男，博士研究生。主要研究方向：高超声速气动热与热防护、高超声速多物理场耦合。Tel．：0451－86402432 E－mail：12B918024＠hit．edu．cn孟松鹤 男，博士，教授，博士生导师。主要研究方向：极端环境与材料响应的耦合问题、新型热防护系统及材料的设计与优化、先进复合材料结构分析与评价。Tel．：0451－86417560 E－mail：mengsh＠hit．edu．cn

＊Corresponding author．Tel．：0451－86417560 E－mail：mengsh＠hit．edu．cn