TMD对大跨径人行桥竖向振动控制效果研究

樊 慧

（山西省交通科学研究院，山西 太原 030006）

0 引言

随着经济发展和城镇化进程加快，城市人口和车辆快速增加，城市道路红线宽度日益加大，为保障机动车车流畅通和行人过街安全，在快速路、车流人流密集主干路往往需要设置人行过街天桥。随着道路宽度增加，大跨度人行天桥日益增多。由于桥梁跨度大、施工环境复杂、上部荷载小，所以往往以钢结构简支梁居多。钢结构材料具有的轻质纤柔特点，降低了桥梁整体的刚度，降低了桥梁的固有频率[1]。导致桥梁自振频率接近人行走的频率，容易产生共振，出现行人行走舒适度下降、桥梁结构安全性降低、桥梁使用寿命降低等后果。《城市人行天桥与人行地道技术规范》[2]要求天桥上部结构竖向自振频率不应小于3 Hz，因此需要采取措施，提高桥梁固有频率。但在人行桥的跨度受到比较严格的控制情况下，通过提高截面的刚度往往附带结构质量的增加，因此很难有效提高人行桥自振频率。相比之下，采用调频质量阻尼器(TMD)限制人行桥动力响应的方法可以保证桥梁结构在发生共振时振幅和加速度满足设计要求，保护桥梁结构安全和保障桥梁使用舒适性，同时具有很大的灵活性、造价较小等优点，近年来在实际工程中得到广泛的应用。

本文首先介绍不同规范对人行荷载模型和人行桥舒适性指标的规定，阐述了TMD的振动控制机理和参数优化，然后以西安某大跨人行拱桥为研究对象，选择合理的人群激励荷载，分析对比了TMD安装前后人行桥的通行舒适性，为人行桥的减振控制设计提供依据。

1 行人荷载模型及人行桥舒适性评价指标

1.1 行人荷载模型

目前各国对人行激励荷载的规定均采用傅里叶级数形式表示荷载模型，且各种荷载模型均只考虑一阶谐波激励，高阶谐波激励并未考虑。

1.1.1 德国行人荷载模型标准

德国人行桥设计指南EN03(2007)依据人流密度，给出了两种不同的荷载模型。人流密度划分为：人流密度d＜1.0人/m2的正常通行人流；人流密度d≥1.0人/m2的高密度人流。两种荷载都是均匀分布的谐波荷载，单位:N/m2，代表在进一步计算中的等效行人流。两者具有相同的表达式：

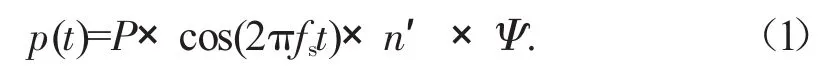
其中：d＜1.0人/m2时，n′1/m2；当 d≥1.0人/m2时，n′

式中：fs为步频；P为当步频为fs时，单个行人产生的荷载幅值，竖向作用时为280 N；S为加载面积；n′为加载面积为S时的等效行人密度；n为加载面积为S时的人数；Ψ为折减系数，当步频接近基频临界值的概率而引入；ξ为结构的阻尼比。

1.1.2 英国行人荷载模型标准

英国规范将桥梁分为简单人行桥 (上部结构为简支，对称单跨，或两到三跨的连续等截面梁桥)和其他人行桥，简单人行桥的最大竖向加速度由简化方法算得。其他人行桥假设行人荷载为一个沿着桥梁纵向以匀速作用在人行桥上的动荷载，且规定单个行人竖向荷载为：

当时 f＜4 Hz时，

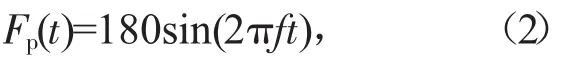
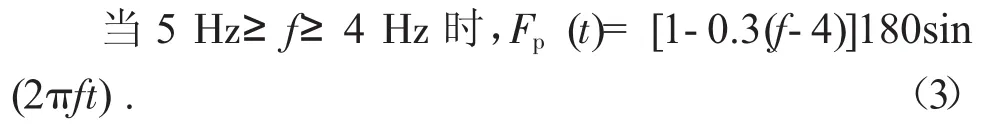
式中假定人行步幅为0.9 m，分析中偏安全地将行人步频取无活载时的人行桥的竖弯基频。该规范没有考虑人群荷载的影响。

1.2 人行桥舒适性评价指标的规定

尽管德国EN03（2007）规范、英国BS5400规范均采用峰值加速度作为评判人行桥通行舒适度的指标，但规范具体的规定有所不同。德国规范共推荐了4个舒适度级别，英国规范只对基本固有频率竖向小于等于5 Hz或横向小于等于1.5 Hz的情况作出要求。具体要求如表1。

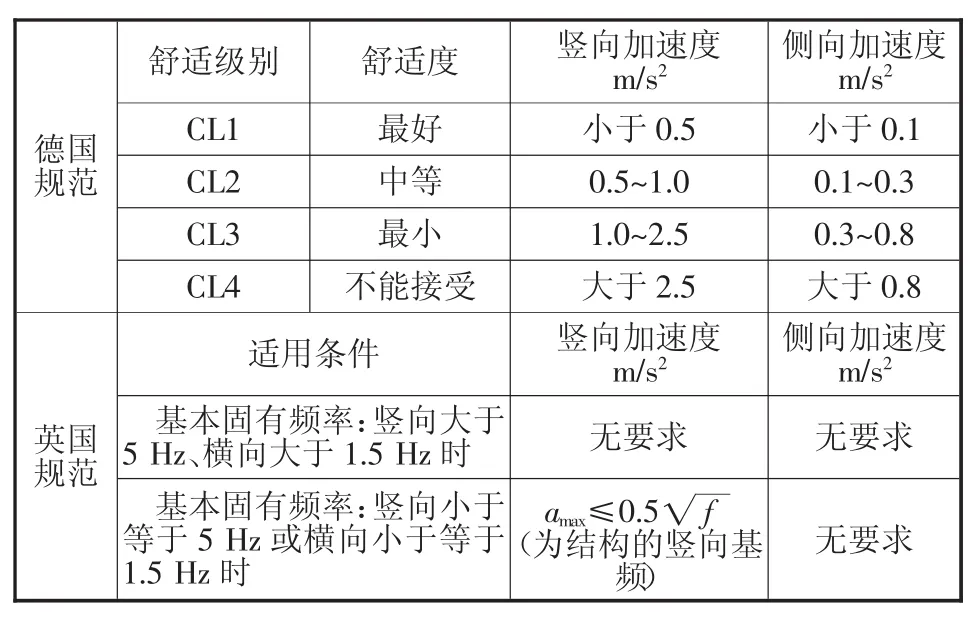
表1 德国、英国规范中舒适度指标

2 调频质量阻尼器（TMD）的参数优化

调频质量阻尼器（TMD）是一种被动控制体系，由主结构和附加在结构上的子结构（固体质量和弹簧减振器等）组成。通过调整子结构的自振频率，使其尽量接近主结构的基本频率或激励频率。当主结构受激励而振动时，子结构就会产生一个与结构振动方向相反的惯性力作用在结构上，使主结构的振动反应衰减并受到控制，如图1所示。调频质量阻尼器减振控制存在有效控制的激励频宽问题，一般来说，装设一个子结构，只能对以某个频率为主的外部激励进行有效减振控制。其主要参数包括TMD阻尼器的质量与主结构的质量比μ、最优频率比fopt和最优阻尼比 ξopt。

图1 TMD系统减振示意图

Den Hartog[3]给出TMD的最优参数设计解析解，如式（4）、式（5）所示：

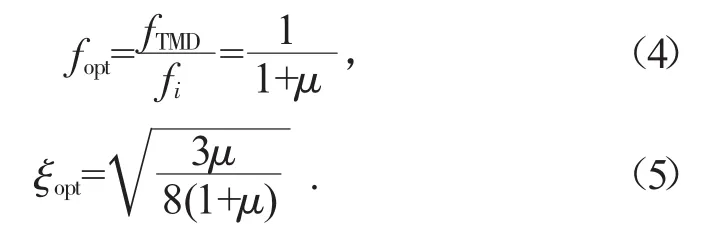
首先确定结构的自振频率及标准化振型，并求得广义振型质量Mi；选取想要控制的第i阶振型，相应的频率为fi，由此计算TMD系统的质量、刚度、阻尼分别为：

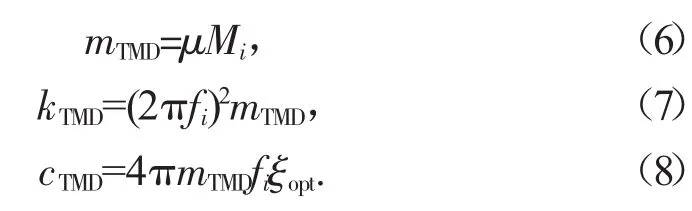
值得注意的是，式（4）和式（5）是在外部激励为简谐荷载，以主体结构位移在一定激励频率范围内最小为目标推导得到的，且该解析近似成立的条件是主体结构的阻尼比为零或者较小。

3 TMD对人行桥的振动控制分析

3.1 桥梁模型的建立

本文以西安某主跨87 m人行天桥为研究对象，通过迈达斯（Midas Civil 2015）软件建模进行分析。在模型中，用桁架单元模拟吊杆和系杆，用空间梁单元模拟其余构件。对空间模型进行特征值分析，结构前四阶的主要振型及频率模拟结果如表2。

表2 模拟桥梁前四阶的主要振型及频率 Hz

从表中可以看出，人行桥的面内一阶竖向频率仅为1.45 Hz，不满足《城市人行天桥与人行地道技术规范》规定的不小于3 Hz要求。

3.2 行人荷载及TMD系统参数计算

3.2.1 行人荷载参数计算

依据人流密度和TMD按照情况，将计算工况分为表3所示4个工况。

表3 模拟桥梁前四阶的主要振型及频率

然后对各工况条件下人群的具体参数进行计算。依据德国规范，将行人荷载作为人群激励荷载，将振幅方向相同的均布面荷载等效为一个作用在振动最大处集中力。根据一阶振型，在桥梁1/4和3/4处附近振幅最大处施加与振幅方向相同的简谐集中力荷载。其中Ψ考虑偏安全取1，简谐力的频率取桥梁一阶振型的频率1.45 Hz。人群荷载的计算如表4所示。

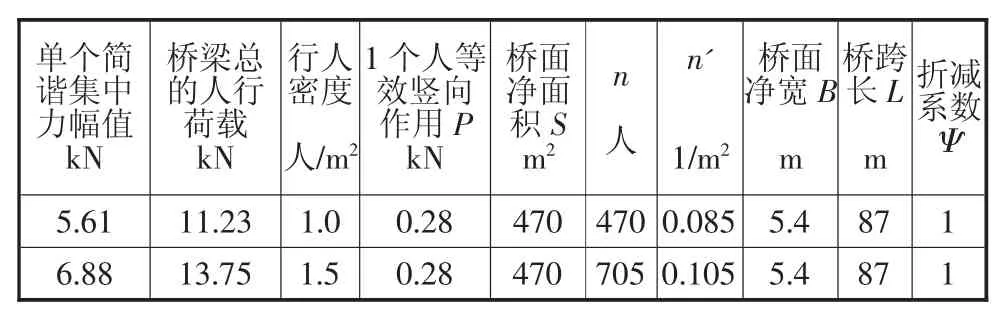
表4 人群荷载计算

3.2.2 TMD系统参数计算

本文采用一般连接特性中的“弹簧和线性阻尼器”，并在连接一端附上TMD的质量来模拟TMD系统，如图2所示。

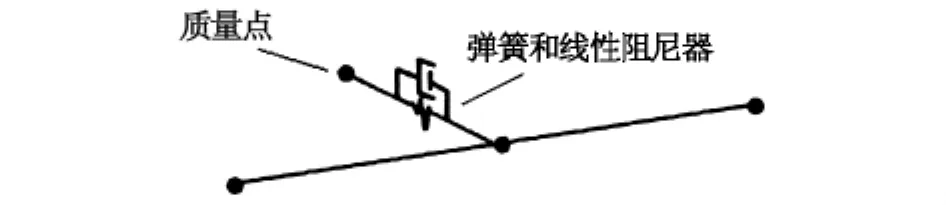
图2 TMD模拟示意图

单个TMD的质量为2.3 t，依据上述TMD的最优参数计算公式，计算出TMD的刚度和阻尼系数为163 kN/m和6.26 kN·s/m。依据设计在距跨中20 m的两侧分别设置两组TMD，全桥共设置4组。

3.3 计算结果分析

各个工况的控制点加速度时程如图3所示。

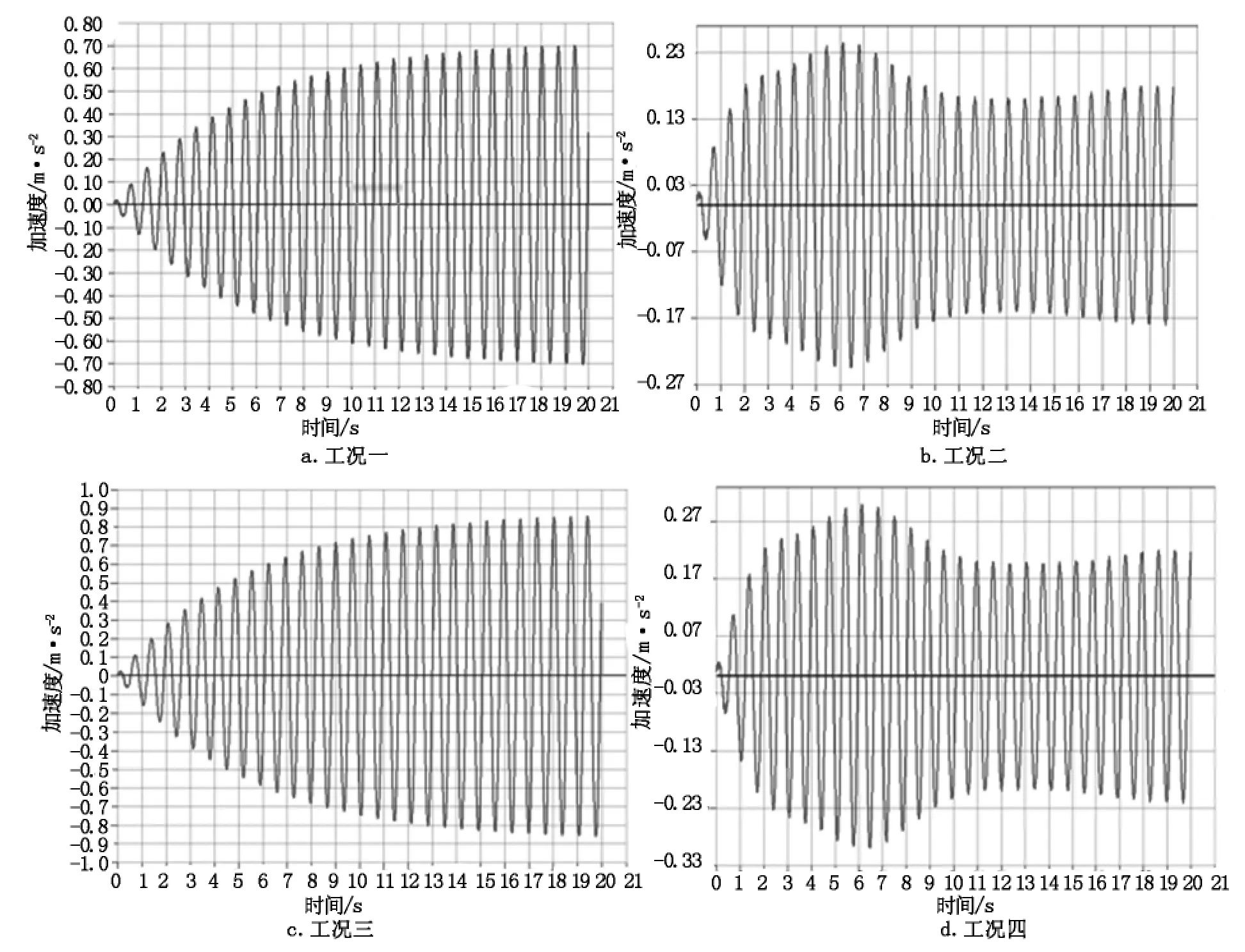
图3 各个工况的控制节点加速度时程图

从图3可以看出，工况一至工况四的结构最大加速度分别为为 0.70 m/s2、0.25 m/s2、0.86 m/s2和0.30 m/s2。从计算结果可以看出，当不采用TMD时，工况一和工况三的最大加速度均大于0.5 m/s2，不满足人群最优舒适度的要求；当采用TMD后，工况二和工况四的人行桥的最大加速度均小于0.5 m/s2，人行桥的振动得到有效控制，满足人群最优舒适度的要求。可见TMD对人行桥振动控制有很好的效果。

4 结论

本文通过对采用TMD的人行桥竖向振动控制的研究，得到以下结论：

a）针对人行桥激励荷载和舒适性评价，各国规范有不同标准，但激励荷载方面均采用未考虑高阶谐波激励的一阶谐波激励荷载模型，人行桥舒适性评价方面均采用峰值加速度指标作为评判标准。

b）将西安某人行桥实际工程作为对象，验证了TMD对大跨度人行桥竖向加速度控制效果，表明TMD能有效提高人行桥的通行舒适度。