教育“无痕”精彩“有迹”（三）——以“平均数”一课的教学为例

江苏苏州工业园区车坊实验小学　徐斌

教育“无痕”精彩“有迹”（三）——以“平均数”一课的教学为例

江苏苏州工业园区车坊实验小学徐斌

徐斌江苏省特级教师，中学高级教师，江苏“人民教育家工程”培养对象，教育部“国培计划”首批特聘专家，人大复印报刊资料《小学数学教与学》编委。

1992年获江苏省小学数学优质课比赛第一名，2000年获全国小学数学观摩课评比一等奖。曾应邀为全国第五届小学数学学术年会上观摩课，在《小学教学研究》等20余家刊物发表论文400余篇，应邀到全国20多个省、市、区讲学400余次。教育事迹在《人民教育》“名师人生”栏目专题报道，《中国教育报》曾七次连载“徐斌教育教学艺术系列报道”。出版有专著《追寻无痕教育》《为学生的数学学习服务》《推敲新课程课堂》《另类课堂》及“中国名师”系列教学光盘。其教育主张是无痕教育，课堂教学风格稳健厚实。

编者注：《小学教学研究》（教学版）2012年第8期和2015年第9期分别刊登过著名特级教师徐斌的两篇同题文章，副标题分别是“以数与代数的教学为例”“以解决问题的策略教学为例”。

无痕教育，从字面上理解是把教育的目的与意图隐蔽起来，通过间接和暗示的方式，对学生进行教育的一种形态。其实无痕教育不仅是一种教育方式，更是一种教育思想，是一种教育心理学的规律和原则，是一种教育的美学和哲学境界，是一种对教育本原的追寻。

为什么在小学数学教育中可以实施无痕教育呢？主要基于以下三点：

一是数学学科的特点。数学是研究客观世界中的数量关系和空间形式的一门科学。小学数学属于初等数学的范畴，它揭示的是现实世界中最简单的数量关系和几何形体等知识，小学数学课程在内容呈现上具有由浅入深、由易到难、循序渐进和螺旋上升的特性。可见，小学数学的学科特征为在数学教学中实施无痕教育提供了充分的可能。

二是儿童认知的规律。数学是思维的体操，儿童学习数学的过程是数学思维活动的过程。儿童思维的发展经历着从低级到高级、从不完善到完善的发展过程。小学儿童思维的基本特点是从以具体形象思维为主要形式逐步过渡到以抽象逻辑思维为主要形式。数学思维是一种内隐性活动，而且各种思维方式之间的彼此相连、融会贯通和发展变化本身就处于一种无痕的状态。

三是课堂学习的本质。学习的本质是发展，课堂学习是为了促进儿童的发展。小学数学教学的过程应该是遵循儿童数学学习的思维规律和小学数学学科课程的基本特性，通过教师的智慧，把作为科学的数学转化为作为学科的数学，把“学术形态的数学”转化为“教育形态的数学”，引导学生在无痕中学习数学和发展能力，感悟思想和提升素养，同时使他们获得丰富的情智体验。

在小学数学教学中，如何实施“无痕教育”呢？笔者试以“平均数”一课的教学为例，谈四点教学策略。

1.不知不觉中开始

有效的课堂学习是如何开始的？让学生在悄无声息中自然而然地开始学习是无痕教育的基本追求。要做到不知不觉中开始学习，需要老师根据儿童的数学现实和生活经验，设计生动丰富的课堂引入环节，让学生油然而生学习热情，使学习的开始像呼吸一样自然无痕。

《平均数》一课的引入部分，我采用了儿童喜闻乐见的套圈游戏情境，通过四次套圈比赛，让学生担任比赛评委，逐渐产生了学习平均数的内在需要。

图1

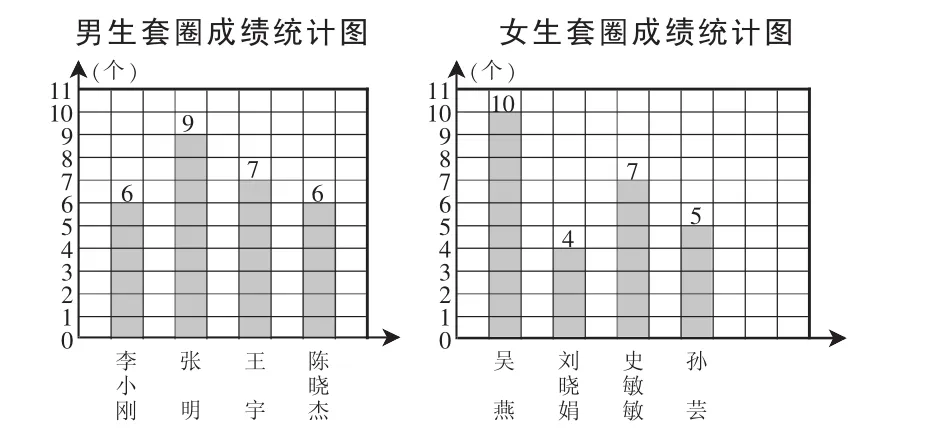
图2

图3

图4

第一场比赛（图1），人数相同，每人套中个数也相同，观察条形图就一目了然，可以判定男生整体水平高；第二场比赛（图2），人数相同，每人套中个数不同，分别求和可以判定男生队获胜；第三场比赛（图3），人数不同，每人套中个数相同，观察条形图也能判定男生队整体水平高；第四场比赛（图4），人数不同，每人套中个数也不同，无法分别求和比较，也不能直接观察统计图获得结果。这样，就迫切需要学习一个新的统计量——平均数来判定结果。

纵观以上课堂引入部分的设计，紧紧围绕与新知相关的数学问题展开：为什么需要学习平均数？平均数与哪些旧知相关？生活中的平均数是怎样产生的？如何从旧知中自然生长出新知？如何通过问题情境产生认知冲突？这样的课堂起始阶段设计，看上去是师生之间不经意的谈话聊天，看上去是生活中常见的游戏比赛，看上去是邀请学生担任套圈比赛的评委，看上去是学生之间讨论并评判比赛结果，实际上，学生不知不觉中产生了对数据统计的需要，并在数据分析中产生了认知矛盾和冲突，使得新知在旧知中自然无痕地生长出来。

2.潜移默化中理解

“为理解而教”一直是课堂教学的重要目标。儿童是如何理解知识的？儿童的思维过程有着怎样的规律？研究表明，小学阶段儿童的认知水平属于“具体运算思维”阶段，其最大特点是思维离不开具体事物的支持，这也导致儿童的感知觉、观察力和记忆均处于初步发展水平，其学习数学的动机和兴趣很不稳定。乌申斯基说过：“儿童是依靠形状、颜色、声音和感觉来进行思维的。”因此，要让儿童获得对知识的理解，需要充分借助形象直观的教学手段，充分利用新旧知识的相互作用，让儿童在不露痕迹中获得新知意义，在潜移默化中理解数学本质。

平均数作为刻画一组数据集中趋势的一种统计量，学生在学习过程中常常有三种理解水平：一是概念理解，二是算术理解，三是统计理解。概念理解十分抽象，不符合儿童的认知特征；算术理解则主要体现为先求和再平均分的程序性计算，比较单一；而统计理解则是建立在数据分析的基础上，寻找能够表达一组数据的代表，从而刻画这组数据的整体水平。

为帮助学生理解平均数的意义，教者采用直观的条形统计图，让学生结合图形进行观察和思考，通过移多补少的方法，得出每人都同样多，再通过移动后得到的平均数画线活动，直观感知平均数的范围。在此基础上进一步提问：除了在统计图上用移动小方格的方法求出平均数，还可以怎样算出平均数呢？学生讨论并尝试后得出：6+9+ 7+6=28（个），28÷4=7（个）。然后比较：用移多补少与求和平分的方法都能求平均数，你觉得这两种方法各有什么特点？

这样的新知教学过程，学生不仅了解了平均数的产生源头，还直观理解了平均数的范围和含义，进而掌握了求平均数的基本方法，获得了对平均数的深刻理解。同时也启示我们，良好的数学理解过程需要依托儿童的思维特征，发挥动作思维和形象思维的作用，在潜移默化中逐步发展抽象思维能力，达成对数学知识和方法的本质理解。

3.循序渐进中掌握

从理解知识到掌握技能，是学生学习数学过程中不可或缺的环节，而掌握技能的过程，既不可能一蹴而就，也不能机械重复单调操练，而应让学生在层层递进中循序渐进地掌握方法、形成技能。

在学生初步理解了平均数的含义之后，知道求平均数可以有两种方法：移多补少法与求和平分法。移多补少法比较直观，有利于学生在求平均数的过程中判断平均数的范围，了解平均数的由来；求和平分法比较抽象，有利于学生用算术思维简便快速地计算出平均数。但是对于初学平均数的学生来说，主要问题是：何时运用移多补少法？何时运用求和平分法？鉴于此，教者做了如下细腻的层次性设计。

第一层次：观察笔筒的实物图（如图5），快速求出平均数。（大多数学生采用移多补少法）

图5

第二层次：笔筒图渐变为竖着画的条形图（如图6）。（大多数学生继续采用移多补少法）

第三层次：竖着画的条形图渐变为横着画的条形图（如图7）。（由移多补少到取长补短）

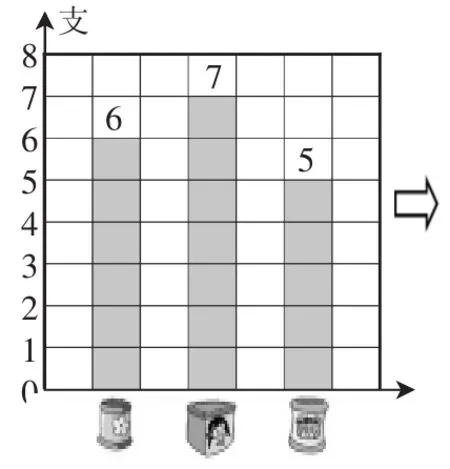
图6

图7

第四层次：由条形图渐变为无数据的丝带图（如图8）。（学生用移多补少法尝试多次，但总是不能准确得出三条丝带的平均长度）

第五层次：丝带图从无数据到有数据（如图9）。（学生自觉采用求和平分法计算）

图8

图9

以上五个层次的设计，从实物图到条形图再到丝带图，从生活到数学再回到生活；从竖着画的条形图到横着画的条形图，从移多补少联想到取长补短；从无数据的丝带图到有数据的丝带图，从移多补少法的不便到求和平分法的简便。在循序渐进的过程中，学生既了解了移多补少法的不足，也产生了对数据的内在需要，从而体验了求和平分法的价值，在不露痕迹中完成了从移多补少法到求和平分法的过渡，进而掌握两种方法的内在本质。

4.春风化雨中提升

无痕教育理念指导下的数学课堂，是学生享受教师悉心服务的过程，也是学生自主学习主动发展的过程，是师生之间和谐互动走向智慧的过程。建立了数学模型之后，为了让学生对初建模型有充分的感性积累，应该让学生运用数学模型解决问题。在解决问题的过程中，积累数学活动经验，获得对数学模型的深刻理解，形成初步运用数学模型的相关技能，感悟数学思想，培养数学素养。

本课在学生理解了平均数的意义与方法之后，设计了三个应用性很强的问题情境：

首先是模拟担任水果店经理。呈现了水果店上周5天里卖出苹果和橘子的数量统计图（如图10），让学生观察思考，主要解决三个方面的实际问题：（1）水果店上周哪天生意最好？哪天生意不太好？请推测一下原因。（2）面对上周的经营现状，作为经理，你会采取什么经营手段？（3）仓库里缺货了，需要多进一些苹果还是橘子？请用数据说明道理。

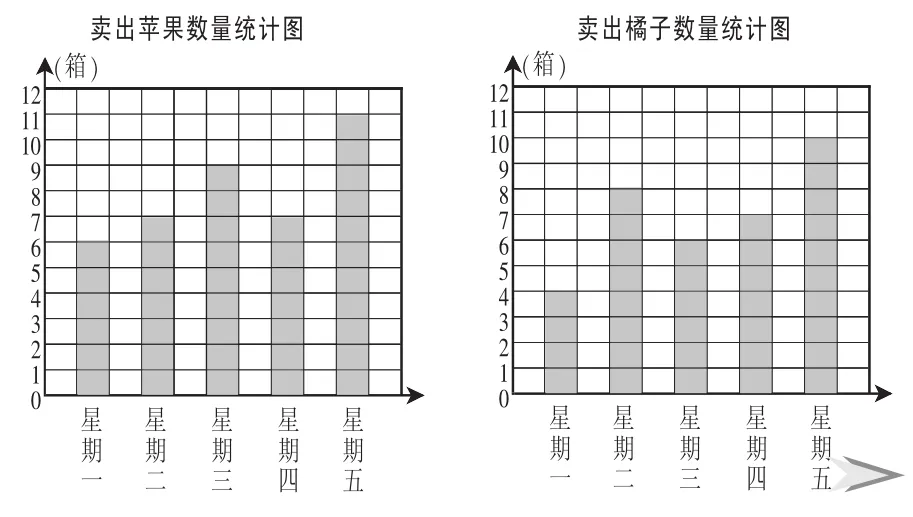
图10

其次是模拟担任篮球队队长（如图11）。提问：李强是篮球队队员，他身高155厘米，可能吗？篮球队可能有身高超过161厘米的队员吗？（显示篮球队5名队员的具体身高统计表）思考：如果姚明加入学校篮球队，平均身高会如何变化？160×5＝800（厘米），800＋226＝1026（厘米），1026÷ 6＝171（厘米）。这时得到的平均身高，具有什么样的特点？为什么原来5名同学的身高都达不到新的平均身高呢？

图11

最后是设计一次套圈决赛活动。比赛规则是：男生人数不变且在第四次比赛的基础上不再重新套圈，又新来了一个女生，据说是高手。要使得女生套圈成绩提高到和男生一样，她必须套中多少个呢？如果女生套圈的准确程度要超过男生，她至少要套中多少个？

良好的数学学习不能止步于教材，应让学生透过数学知识技能的学习获得更为丰富的思想方法，就需要学以致用与融会贯通。以上三个解决实际问题的教学设计，都是在教材的基础上向着思维的深处迈进了一步：从简单的水果数量的平均数计算拓展为数据分析观念的培养，从已知平均数推测数据分布到极端数据干扰带来新的问题思考，从直接计算平均数问题到灵活推理计算与逆向思维发展以及形象思维介入。这样的迈进，使得学生在层层递进中走向了数学的本质，在润物无声中发展了思维能力，在春风化雨中提升了数学素养。♪