有现金流追加的具有随机时域的均值-方差投资策略的研究

梁雪，付文豪，陆晨曦

（苏州科技大学数理学院，江苏苏州215009）

有现金流追加的具有随机时域的均值-方差投资策略的研究

梁雪，付文豪，陆晨曦

（苏州科技大学数理学院，江苏苏州215009）

考虑有随机现金流追加情形下随机时域的均值-方差投资选择问题。首先，建立一个均值-方差模型，用一个随机过程来表示随机现金流；然后，将模型转化为一个确定时域的均值-方差模型；最后，用动态规划的方法得到了最优策略，并进行了数值计算。

M-V模型；动态规划；随机现金流

1952年，马柯维茨证券组合理论的产生标志着现代组合投资理论的开端[1-2]，由此，数理化方法真正进入到投资领域，并迅速发展起来，均值-方差模型因此也成为现代主流金融学的理论基石。可是该模型与实际市场情况还是有一定的差距，计算结果与实际最优策略还是有偏差。为了更贴近证券投资市场的实际情况，许多学者考虑了更加复杂的均值-方差模型，例如郭文旌[3]考虑投资者可能随时终止投资和具有特殊消费的均值-方差模型，王艳萍[4]等提出了多因子结构下的静态均值-方差模型，刘利敏[5]等考虑了基准过程的均值-方差最优投资策略问题，李腊生[6]等考虑了不同类型的投资者对投资策略的影响，伍慧玲[7]等在机制转换模型中用一个随机过程来刻画投资者在投资过程中可能发生的资金的抽出或追加的情况。受此启发，笔者将在随机时域模型中考虑有随机现金流追加情况下的均值-方差投资选择问题。

1 模型的建立

假设一投资者从0时刻开始进市场投资，到T时刻结束，该投资者的初始财富值为x0，xt为t时刻的财富值，t=0，1，2，…，T-1。设该市场上一共有n+1种证券，其中第0种为无风险证券，其余n种为风险证券，其在t阶段的收益分别为：，t=1，2，…，T，令，投资者在t阶段投资到第i个证券的资金比例为，令，称ut为t阶段的一个投资组合，各个阶段的投资组合的集合称为投资策略，记为u。投资者随时可能停止投资，因而可能只进行了r（≤T）个阶段的投资，假定r的分布概率为：p0=P（r＝0），pi=P（r＝i），（i=1，2，…，T），记r的分布函数为F（t），，t=0，1，2，…，T，pT=1-F（T-1）。除此之外，文中还在t时刻追加一笔随机财富St且与et、ut独立（t=0，1，2，…，T-1），设S0=0。

2 模型的求解

投资者的目的是在随机时域[0，r]内找一个投资策略，使得最终期望最大、风险最小，为此建立模型

E（ω）：maxE（xr）-ωVar（xr），其中

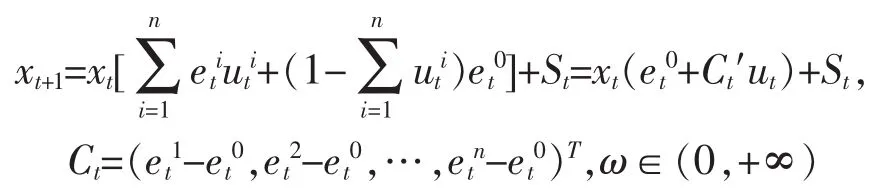
引理1u*∈∏ω，那么u*∈∏A。

引理2如果u*∈∏A，那么u*∈∏ω，其中λ*=1+2ωE（xr）|u*。

由引理1，引理2，可以通过求解问题A（λ，ω）来求得E（ω）的最优策略，A（λ，ω）则通过动态规划来求解。首先，将这个不确定时域的问题转化为确定时域的问题

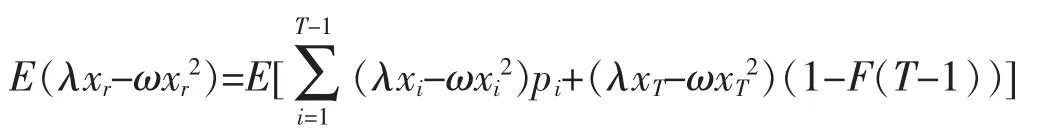
于是A（λ，ω）就等价于以下确定时域的模型

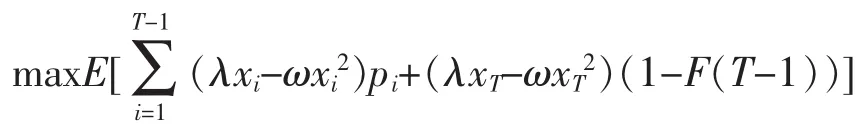
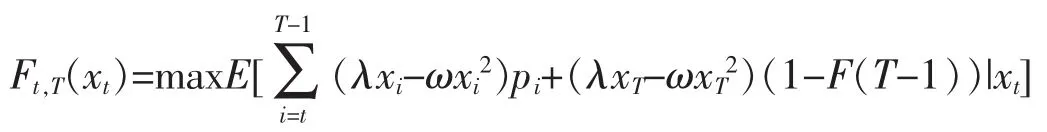
于是

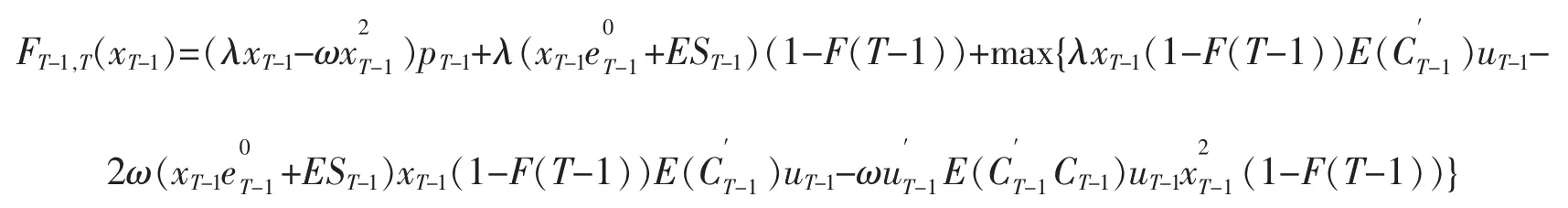
求uT-1的值使FT-1，T（xT-1）达到最大

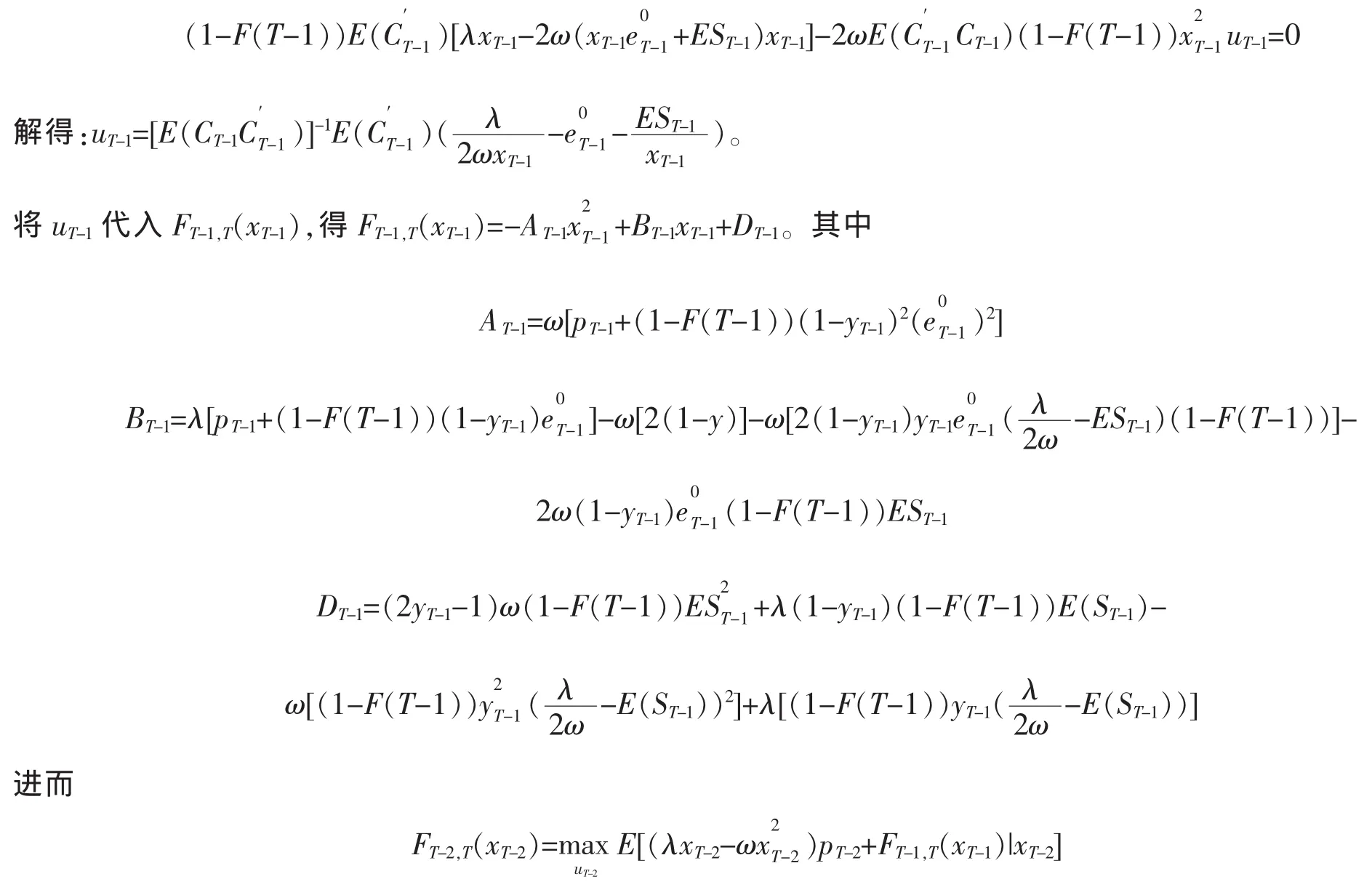
由后往前重复上述过程，反复迭代计算得到

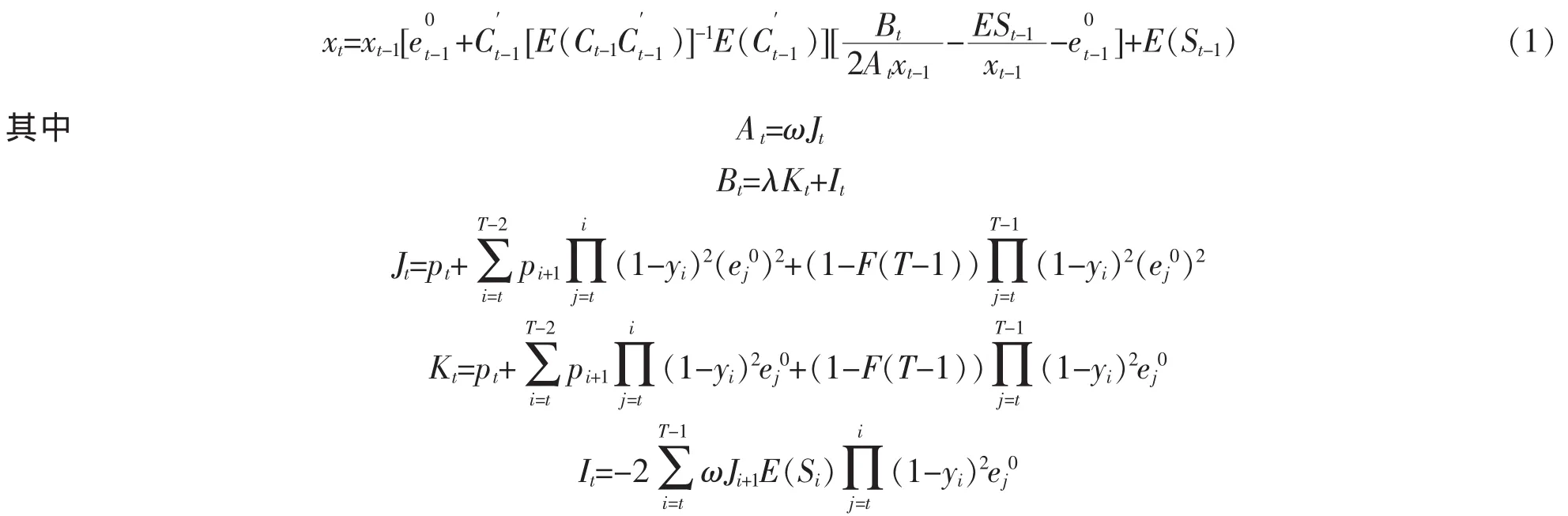
对（1）式两边取期望

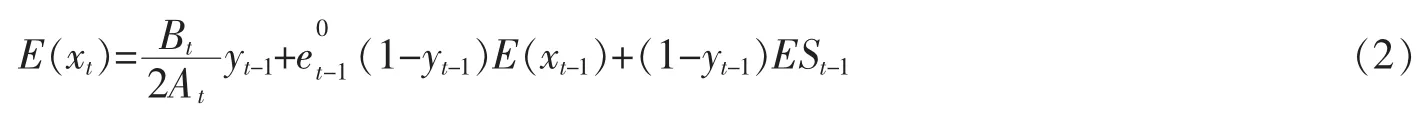
对（2）式反复迭代

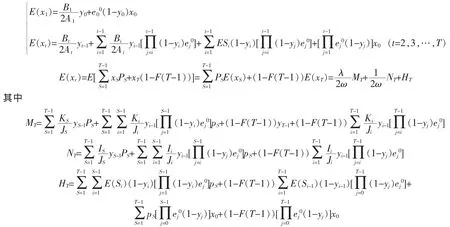
由引理2可知，如果λ*=1+2ωE（xr）|λ＝λ*，即时，u*∈π（λ，ω），u*∈π（ω）。对于给定的参数ω，原问题的最优策略为。其中：。最终财富。

3 数值计算

假设，某投资者要进行为期三年的投资，他的初始资金为20万元，有四种可选择的证券，一种证券是无

风险的，它的利率为1.05，另外三种是风险证券，它的平均收益率与风险分别为

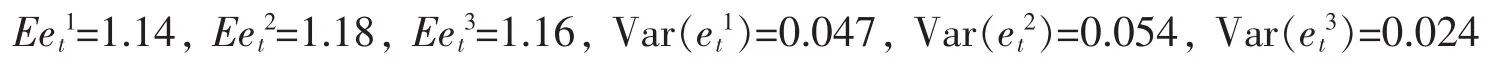
在上面设定的参数下进行数值计算，考虑随机现金流对各阶段投资策略的影响，结果如图1-图4。前三个图的横坐标均表示追加现金流的期望值，纵坐标均表示个资产的最优投资比例，第四个图是有随机时域的均值-方差问题的有效前沿。从这四个图可以看出追加的现金流确实对最优投资策略、有效前沿产生影响。

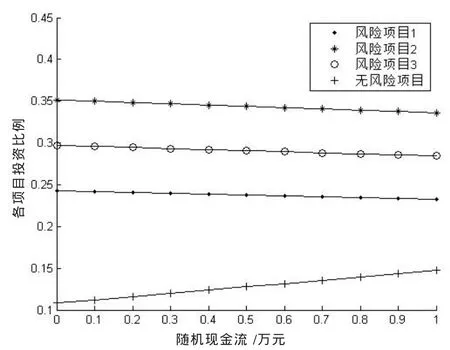
图1 不同现金流，1时刻下的投资方案

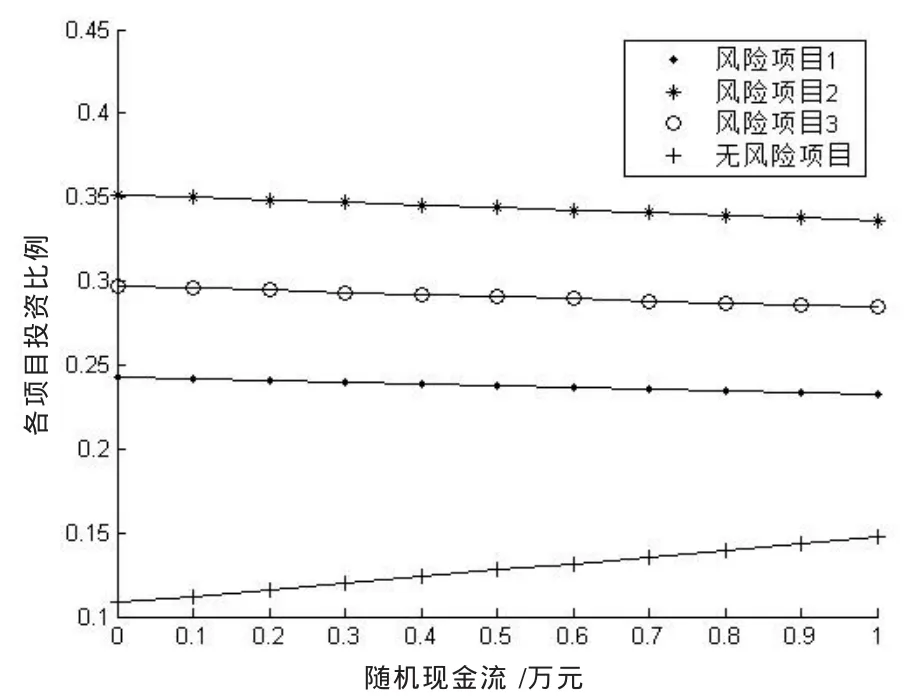
图2 不同现金流，2时刻下的投资方案

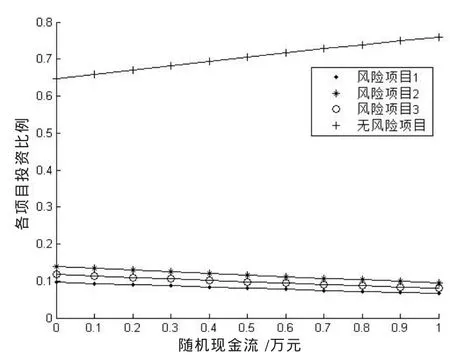
图3 不同现金流，3时刻下的投资方案

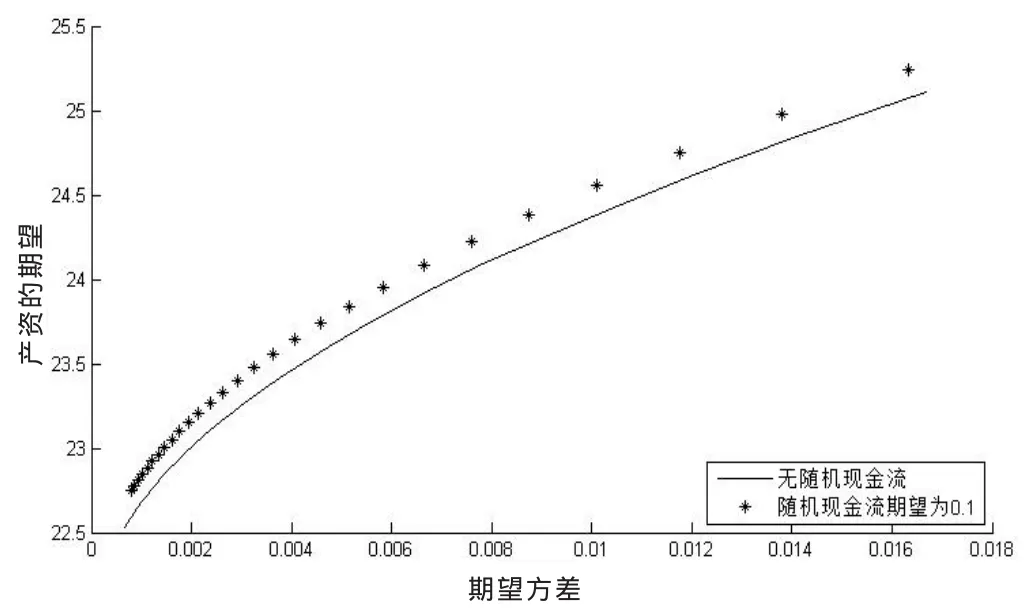
图4 有效前沿

[1]朱书尚，李端，周迅宇，等.论投资组合与金融优化——对理论研究和实践的分析与反思[J].管理科学学报，2004，7（6）：1-12.

[2]郑振龙，陈志英.现代投资组合理论最新进展评述[J].厦门大学学报（哲学社会科学版），2012（2）：17-24.

[3]郭文旌.M-V最优投资组合选择与最优投资消费决策[D].西安：西安电子科技大学，2003：43-55.

[4]王艳萍，陈志平，陈玉娜.多因子投资组合选择模型研究[J].工程数学学报，2012，29（6）：807-814.

[5]刘利敏，肖庆宪.基于基准过程的动态均值-方差最优投资组合选择[J].数学的实践与认识，2013，43（1）：1-8.

[6]李腊生，刘磊，李婷.基于投资者异质性的投资组合选择与证券市场价格[J].统计研究，2013，30（2）：40-48.

[7]WU Huiling，LIZhongfei.Multi-period mean-variance portfolio selection with regime switching and a stochastic cash flow[J].Insurance：Mathematics and Economics，2012，50：371-384.

[8]LIDuan，NG Wanlung Ng.Option dynamic portfolio selection:multiperiod Mean-Variance formulation[J].Mathematical Finance，2000，10（3）：387-406.Study on investing strategies of mean-variance selection with a stochastic cash flow and random time horizon

LIANG Xue，FU Wenhao，LU Chenxi
（School of Mathematics and Physics，SUST，Suzhou 215009，China）

In this paper，we have studied the multi－period mean－variance portfolio selection with a stochastic cash flow and random time horizon.Firstly,we built a mean－variance model,and represented the stochastic cash flow by a stochastic process.Then，we transformed the model into one with determined time domain.Finally，we obtained the analytical optimal multi－period portfolio strategy with the method of dynamic programming and provided the numerical results.

M－V model；dynamic planning；stochastic cash flow

O224MR（2000）Subject Classification：91B28；91B70

A

1672－0687（2016）04－0009－04

责任编辑：谢金春

2014－07－16

国家自然青年科学基金资助项目（11401419）；江苏省自然科学青年基金资助项目（BK20140279）；本科生“实践创新训练计划项目”（201410332060X）；“本科教学工程”教学改革与研究项目（2013JGZ-10）

梁雪（1978-），女，湖北麻城人，副教授，博士，研究方向：金融数学。