Multisource least-squares reverse-time migration with structure-oriented filtering*

Fan Jing-Wen, Li Zhen-Chun, Zhang Kai♦, Zhang Min, and Liu Xue-Tong

Multisource least-squares reverse-time migration with structure-oriented filtering*

Fan Jing-Wen1,2, Li Zhen-Chun1,2, Zhang Kai♦1,2, Zhang Min1,2, and Liu Xue-Tong3

The technology of simultaneous-source acquisition of seismic data excited by several sources can significantly improve the data collection efficiency. However, direct imaging of simultaneous-source data or blended data may introduce crosstalk noise and affect the imaging quality. To address this problem, we introduce a structure-oriented filtering operator as preconditioner into the multisource least-squares reverse-time migration (LSRTM). The structure-oriented filtering operator is a nonstationary filter along structural trends that suppresses crosstalk noise while maintaining structural information. The proposed method uses the conjugate-gradient method to minimize the mismatch between predicted and observed data, while effectively attenuating the interference noise caused by exciting several sources simultaneously. Numerical experiments using synthetic data suggest that the proposed method can suppress the crosstalk noise and produce highly accurate images.

Simultaneous-source acquisition, blended data, least-squares migration, structureoriented filtering

Introduction

Compared with the one-way wave equation migration, reverse-time migration (RTM) (Baysal et al., 1983; McMechan, 1983; Whitmore, 1983; Zhang et al., 2007; Casasanta et al., 2015; Xue et al., 2015) directly solves the two-way wave equation. Consequently, it is a powerful method for highly accurate imaging of complex subsurface structures. RTM typically uses cross-correlation as imaging conditions, whereas the imaging conditions of conventional cross-correlations are the adjoint operator of the Born modeling operator rather than its inverse (Lailly, 1983). When the acquisition aperture and bandwidth of the wavefield are limited, the conventional cross-correlation imaging condition only images the subsurface structure fuzzily. To solve this problem, we regard the seismic migration as a linear inverse problem and then minimize the error functional by the gradient method to obtain the imaging results. This approach is often called least-squares migration (LSM). The early development of the leastsquares migration was primarily based on the Kirchhoff migration operator (Lambare et al., 1992; Nemeth etal., 1999). Then, the one-way wave equation migration was developed (Kueh and Sacchi, 2003; Wang et al., 2005; Huang et al., 2014).The least-squares reversetime migration (LSRTM) based on the two-way wave operator method was recently implemented (Dai et al., 2012; Liu et al., 2013; Zhang et al., 2013b; Xue et al., 2014; Li et al., 2014; Hou and Symes, 2015; Huang et al., 2015; Liu et al., 2016).

The imaging results with LSM have better amplitude balance, better resolution, higher fidelity, and fewer migration artifacts than in conventional migration. Therefore, it can be applied to suppress the crosstalk noise caused by the direct imaging of simultaneoussource data. Beasley (2008) proposed the simultaneoussource acquisition technique, which allows more than one source to be activated at different points and at the same time to obtain the blended data from multiple sources. This approach can effectively reduce the acquisition cost. Currently, the imaging of blended data is divided into two kinds. The first method firstly separates the blended data and then applies conventional migration for imaging, whereas the second method directly images the blended data (Wang et al., 2013; Wang et al., 2014; Lu et al., 2015). The first method reduces the processing efficiency and the separation becomes more difficult when the blended source interval is small. Therefore, we study the direct imaging of blended data because of the high efficiency of the method. Nevertheless, the disadvantage of this method is that it introduces coherent crosstalk noise into the migration section owing to the different gathers, which affects the imaging accuracy.To suppress the crosstalk noise, we use LSM to perform direct imaging of simultaneous-source data (Dai and Schuster, 2009; Tang and Biondi, 2009; Schuster et al., 2011; Huang and Schuster, 2012). However, conventional least-squares migration cannot quickly eliminate the effect of crosstalk noise on the imaging results. Therefore, to ensure the stability of the inversion and improve the inversion results, it is important to select reasonable constraint conditions.

Reasonable constraints are important in inversion. Since the least-squares migration was proposed, many have worked on the least-squares migration constraint conditions. Kuehl and Sacchi (2003) used smoothing regularization along the ray parameter axis in LSM to suppress migration artifacts because of irregular sampling. Wang and Sacchi (2009) used the F–X prediction filtering operator, as a structureenhancing constraint condition, to suppress the acquisition footprints and improve the continuity of the imaging results. Liu et al. (2013a) used two different preconditioners in least-squares migration; they introduced smoothing operators in common image gathers and adopted plane-wave constructors in common offset gathers to suppress the noise owing to irregular sampling. Xue et al. (2016) chose structure-enhancing filtering (Liu et al., 2010) as the shaping regularization operator (Fomel, 2007) and used least-squares reversetime migration to remove the migration artifacts owing to incomplete data or the crosstalk noise owing to simultaneous-source data.

Based on previous studies, we introduce the structureoriented filtering operator (Liu et al., 2014) into the multisource least-squares reverse-time migration as preconditioner and use the conjugate gradient method to solve it. Numerical tests show that the multisource leastsquares reverse-time migration with structure-oriented filtering can suppress the crosstalk noise owing to the direct imaging of blended data, while it preserves the structural information and improves the imaging accuracy.

Theory

Least-squares reverse-time migration

The constant-density acoustic wave equation is

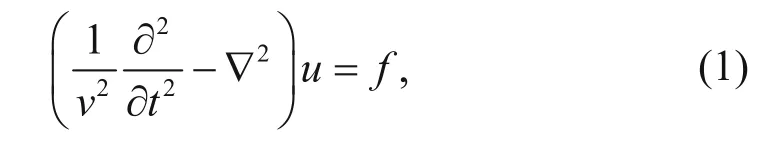
where v is the velocity model, f is the source function, and u is the wavefield.

We assume that the velocity model can be decomposed into the background velocity v0and the velocity perturbation δv (Born approximation) (Beylkin, 1985; Dai et al., 2013)

Similarly, the wavefield can be decomposed into the background wavefield u0and the wavefield perturbation δu (Dai et al., 2013)

Based on the Born approximation, the relation between the wavefield and velocity perturbations are (Dai et al., 2013)

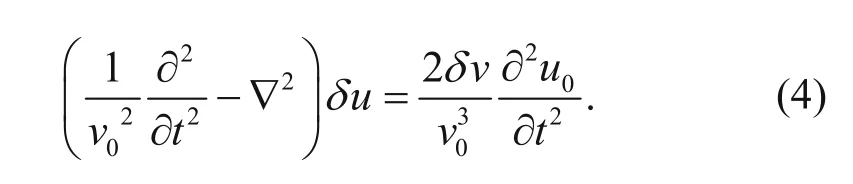
where L is the linear seismic modeling operator and m is the velocity perturbation term. However, the background wavefield typically represents the incident wavefield and the wavefield perturbation represents the reflected wave; therefore, the velocity perturbation term can be used as the reflectivity of the least-squares migration, which is the target model.

The least-squares migration problem is equivalent to the optimization of objective functions. Thus, the regularization objective function of the least-squares reverse-time migration is (Xue et al., 2016)

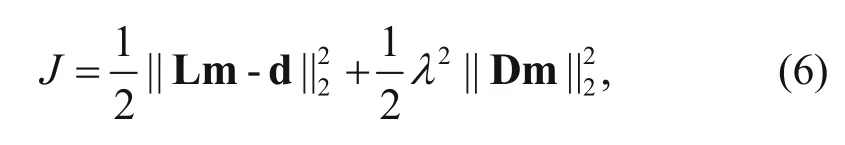
where d is the observed data, λ is the regularization parameter used to adjust the weight between constraints and data residuals, and D is the regularization operator as the a priori information that is used to constrain the imaging results.

The gradient of equation (6) is

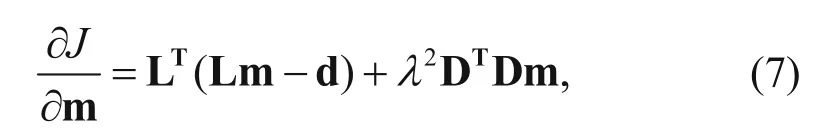
where LTis the adjoint of operator L. In actual solving process, we obtain the gradient using the data residuals of the reverse-time migration.

We make equation (7) equal to zero and obtain the optimal solution of the objective function (6)

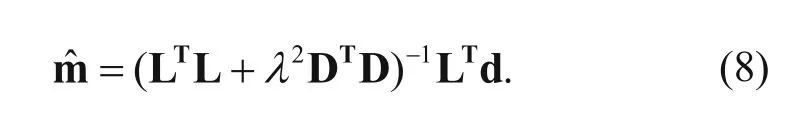
Owing to the difficulty of solving the inverse operator ofdirectly, we normally use multipleiteration optimization methods. In this study, we use the conjugate gradient method.

Multisource least-squares reverse-time migration

Currently, the technology of simultaneous-source acquisition has attracted attention because it allows more than one source to be activated at different points at the same time, and it reduces the acquisition cost and improves the quality of the acquired seismic data. The simultaneous-source data acquisition is expressed as (Berkhout, 2008)

We substitute equation (10) into equation (9) and obtain (Dai and Schuster, 2009)

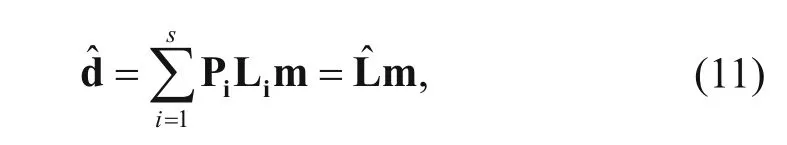
We substitute equation (11) into equation (6) and obtain the objective function of the multisource leastsquares reverse-time migration

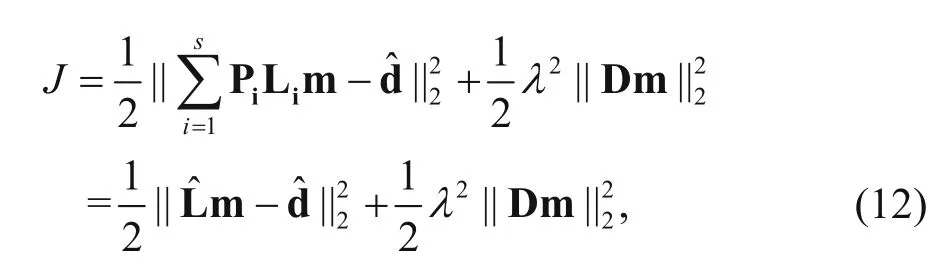
with gradient

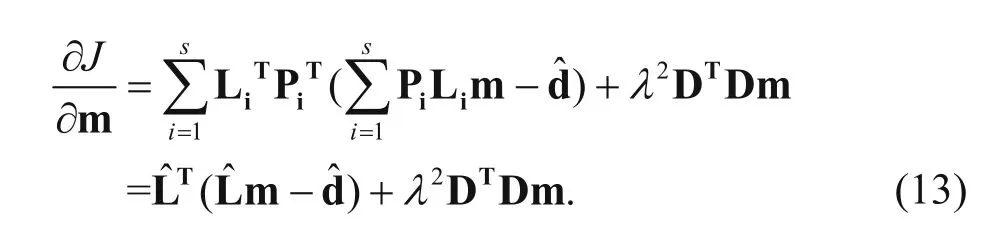
Preconditioning

We introduce a new variable to meet the following relation

We introduce the preconditioner as =-1P D (Liu et al., 2013a) and the objective function is rewritten as

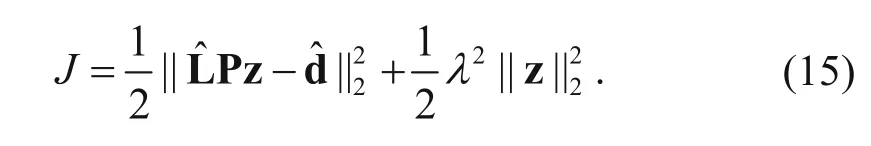
We use the conjugate gradient method to findthe optimal solution z of the objective function. We substitute the solution into equation (14) and then we obtain the final imaging results. To suppress the crosstalk noise owing to the direct imaging of the blended data and preserve structural information as well, we chose structure-oriented filtering as preconditioner.

Structure-oriented filtering

Structural orientation filtering characterizes the structural trend through the local dip of the seismic event. We apply nonstationary filtering along the structural trend to suppress the random noise under the premise of protecting the structural information (Chen, 2015). The structure-oriented filtering is used to extract the formation structure, and Fomel (2010) proposed a structure prediction method based on local dip to obtain the local dip information through the destruction of the plane-wave destruction and to characterize the local plane-wave model of seismic data.

We assume that the seismic section consist of series of seismic tracewhere N is the total number of seismic traces and siis the ith trace data.

The plane-wave destruction can be defined in linear operator notation as (Liu et al., 2010)

where r represents the residuals of the original and predicted seismic traces and D is the nonstationary PWD operator (Fomel, 2002)

where σiis the local dip, Pi,j(σi) is the prediction operator of trace j from trace i, and I is the identity matrix. Therefore, we can estimate the local dip σ by minimizing the residual r using the conjugate gradient method (Fomel, 2002).

We can calculate the prediction operator Pi,jafter we obtain the local slope through equation (17). The prediction of the trace from a distant neighbor can be accomplished by simple recursion. For example, predicting trace k from trace 1 is simply defined as follows (Liu et al., 2010):

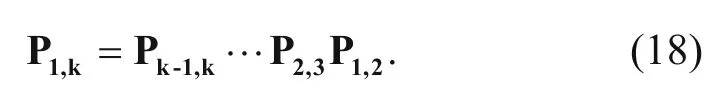
Thus, based on this algorithm and by viewing the prediction steps as the radius, we use the prediction operator to predict the target seismic traces from their neighbors. Compared with the original data, the data volume of the prediction is equivalent to the original data and extended to the dimension of prediction steps (Liu et al., 2010). We can suppress the random noise of the prediction data volume by using the nonstationary filtering along the prediction direction.

Numerical examples

Simple model

As shown in Figure 1, the sample points of the vertical and horizontal velocity models are 350 and 512, respectively, at vertical and horizontal grid intervals of 5 m, the velocity from top to bottom is 1500 m/s, 2000 m/s, 2500 m/s, 3000 m/s, and 3500 m/s. There are 48 shots on the surface, and each shot is recorded by 512 receivers at 5 m intervals. A 25 Hz Ricker wavelet is used as the source wavelet, the recording time is 2.5 s, and the time sampling interval is 0.5 ms. We adapt the simultaneous-source acquisition with two shots excited at the same time to obtain the 24 shot supergathers. Figure 2 shows the blended data.

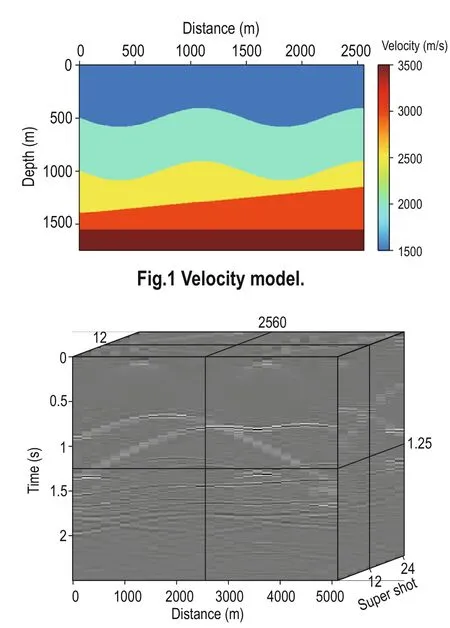
Fig.2 Blended data.

The structure-oriented filtering used in LSRTM requires the local dip information and the accuracy of the local dip information affects the accuracy of the final image. Therefore, we iteratively estimate the local dip information from the result of the previous iteration. The local dip information required for the first iteration can be estimated by the multisource reverse-time migration result.

Figure 3 shows the direct imaging results of simultaneous-source seismic data using different migration methods. Figure 3a shows the RTM image after Laplacian filtering, with high crosstalk noise, amplitude energy imbalance, and low signal-to-noise ratio in the migration section. Figure 3b shows the local dip estimated from the RTM image results, which represents the local dip information required in the first iteration, and we can see from the figure that the local dip information has several large values caused by crosstalk noise. Figure 3c shows the LSRTM image results after 40 iterations. Compared with the RTM image results, the LSRTM effectively compensates the energy of deep reflection events and suppresses parts of the crosstalk noise. We can also see from the figure that the crosstalk noise in the LSRTM migration section remains high. Figures 3d and 3e show the image results after 20 and 40 iterations, respectively, by the multisource LSRTM with structure-oriented filtering. As shown in these figures, the low-frequency noise and crosstalk noise are gradually suppressed when the number of iterations increases. The contrast between Figures 3e and 3c shows that the signal-to-noise of the migration section has significantly improved. Figure 3f shows the local dip information estimated from Figure3e. Compared with Figure 3b, we can see that the large values have disappeared and the estimated local dip information is more accurate.

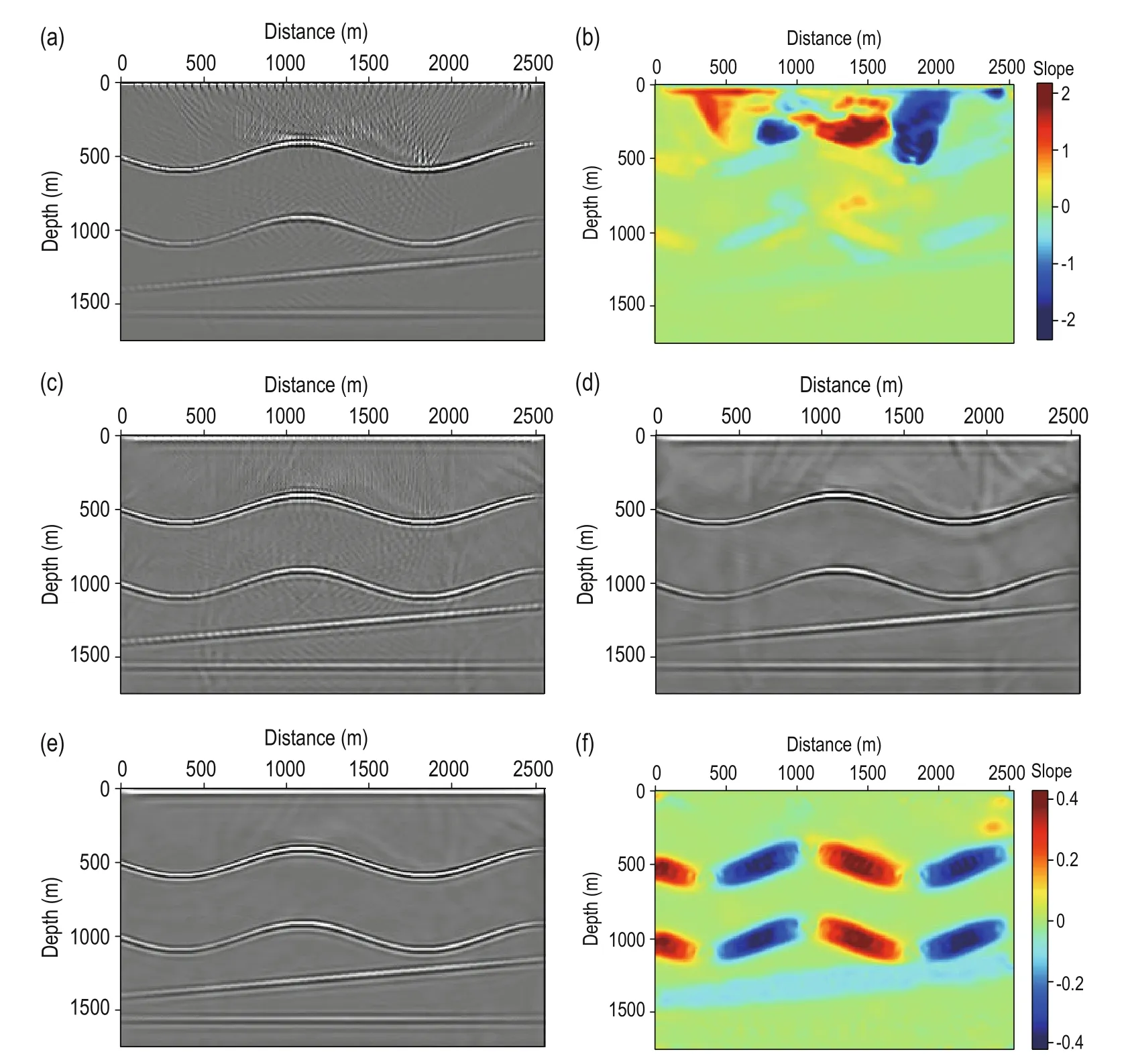
Fig.3 Simple model: (a) RTM image; (b) dip estimated from the RTM image; (c) LSRTM image after 40 iterations; (d) Multisource LSRTM with structure-oriented filtering image after 20 iterations; (e) Multisource LSRTM with structure-oriented filtering image after 40 iterations; and (f) dip estimated from (e).

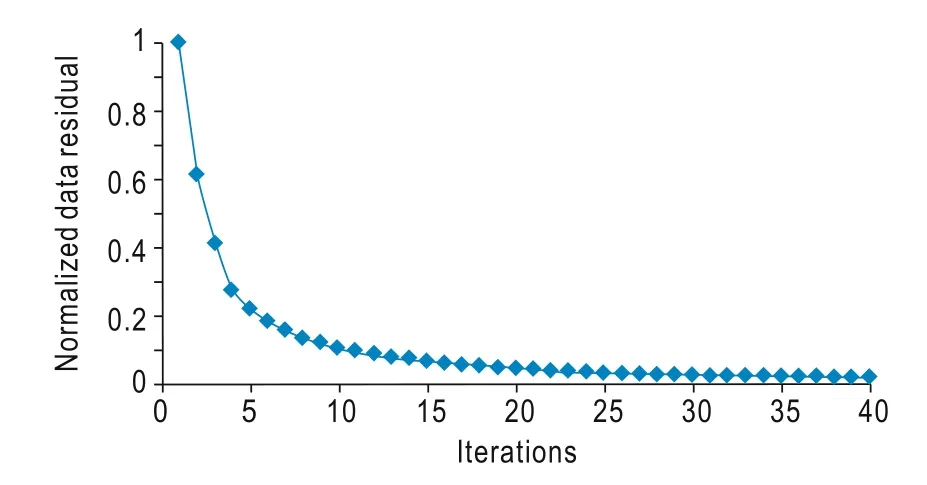
Fig.4 Normalized data-misfit convergence.

Figure 4 shows the convergence of the normalized data residuals for the multisource LSRTM with structureoriented filtering. The figure shows that the normalized data residuals decrease and the inversion results better converge when the number of iterations increases.

Hess model

As shown in Figure 5, the left side of the Hess velocity model contains a high-velocity salt body, with a relatively steep fault plane on the right. The vertical and horizontal sample points are 400 and 905, respectively, with vertical and horizontal grid spacing of 30 m. There are 90 surface shots and each shot is recorded by 905 receivers at 30 m intervals. The source wavelet was a 20 Hz Ricker wavelet, the recording time was 4s, and the time sampling interval was 1ms. For the simultaneoussource acquisition, 5 shots were excited at the same time to produce 18 shot supergathers. Figure 6 shows the blended data.

Figure 7 shows the direct imaging results of the simultaneous-source seismic data using different migration methods. Figure 7a shows the RTM image after Laplacian filtering, with high crosstalk noise in the migration section, amplitude energy imbalance, and subsalt structures that are difficult to image and low signal-to-noise ratio. Figure7b shows the local dipestimated from the RTM image results, which is the local dip information required in the first iteration. We see that the local dip information has large values owing to the crosstalk noise. Figure 7c shows LSRTM image after 60 iterations. Compared with the RTM image results, LSRTM improves the balance of the event energy and suppresses the crosstalk noise, and improves the imaging of the subsalt structure. We can also see that the crosstalk noise on the LSRTM migration section remains high. Figures 7d and show the image results based on the multisource LSRTM with structure-oriented filtering after 30 and 60 iterations. As the number of iterations increases, the low-frequency noise and crosstalk noise are gradually suppressed. From Figures 7e and 7c, wesee that the signal-to-noise ratio of the migration section has significantly improved. The imaging of the fault plane in Figure 7e suggests that the proposed method can effectively suppress the crosstalk noise and preserve the structural information. Figure 7f shows the local dip information estimated from Figure 7e. Comparedwith Figure 7b, we see that the large values have disappeared and the estimated local dip information well characterizes the structural trends.

Fig.6 Blended data.

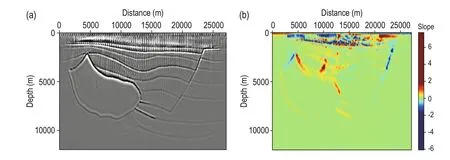
Fig.7 Hess model: (a) RTM image; (b) dip estimated from the RTM image; (c) LSRTM image after 60 iterations; (d) Multisource LSRTM with structure-oriented filtering image after 30 iterations; (e) Multisource LSRTM with structure-oriented filtering image after 60 iterations; and (f) dip estimated from (e).

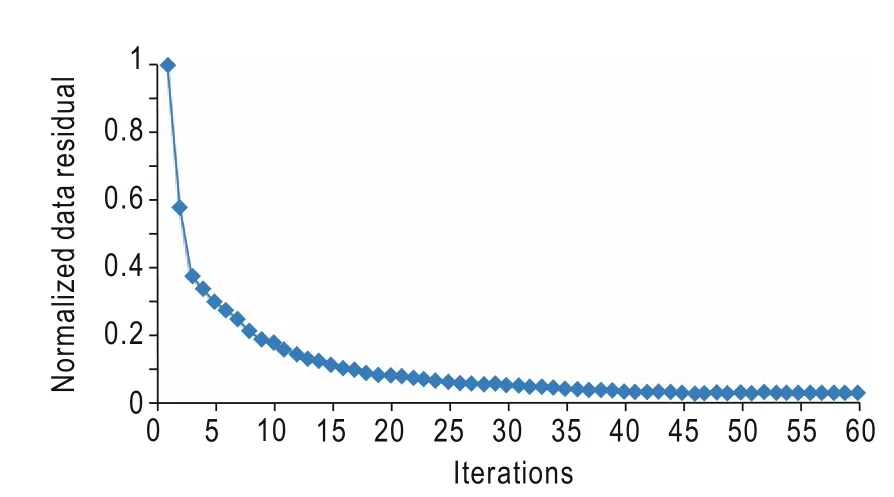
Fig.8 Normalized data residuals convergence.

Figure 8 shows the convergence of the normalized data residuals for multisource LSRTM with structureoriented filtering. The figure shows that the normalized data residuals converge and the inversion imaging is stable.

Conclusions

The simultaneous-source acquisition can greatly reduce the cost of acquisition and obtain blended data from several sources. We discuss the advantage of the multisource least-squares migration with structureoriented filtering to the imaging of blended data. The method negates the error generated during the separation of blended data and has high efficiency. Direct imaging of blended data introduces crosstalk noise; thus, in this paper, we introduce the structure-oriented filtering operator in the multisource least-squares reverse-time migration as preconditioner. The numerical modeling results suggest the following.

LSRTM compensates the energy of deep reflection events, and the structure-oriented filtering operator in the multisource least-squares reverse-time migration effectively suppresses the crosstalk noise owing to thedirect imaging of blended data, improving accuracy.

Structure-oriented filtering uses the local dip of the seismic event to characterize the structural trend. The application of nonstationary filtering along the structural trend suppresses the crosstalk noise and protects the structural information.

The local dip information is important as it affects the accuracy of the final image. Therefore, how to estimate more accurate local dip information will be the focus of the next study.

(4) The proposed method suppresses low-frequency noise and crosstalk noise to improve the accuracy of imaging by gradually increasing the number of iterations. However, comparing with the conventional migration, LSRTM has larger computation. Therefore, the calculation cost and imaging accuracy should be taken into account to select the number of iterations.

Acknowledgements

We wish to thank the SWPI laboratory staff for support and the use of the Madagascar software. We also wish to thank Liang Kai and Liu Linong for their comments.

Baysal, E., Kosloff, D. D., and Sherwood, J. W. C., 1983, Reverse-time migration: Geophysics, 48, 1514-1524.

Beasley, C. J., 2008, A new look at marine simultaneous sources: The Leading Edge, 27, 914-917.

Berkhout, A. J., 2008, Changing the mindset in seismic data acquisition: The Leading Edge, 27, 924-938.

Beylkin, G., 1985, Imaging of discontinuities in the inverse scattering problem by inversion of a generalize Radon transform: Journal of Mathematical Physics, 26, 99-108.

Casasanta, L., Xue, Z., and Gray, S. H., 2015, Converted wave RTM using lowrank wavefield extrapolation: 77th Annual International Meeting, EAGE, Extended Abstracts, N116.

Cheng, C. L., 2015, Key technique and application of structure oriented filter for seismic wave field: PhD Thesis, Jilin University.

Dai, W., Fowler, P., and Schuster, G. T., 2012, Multisource least-squares reverse time migration: Geophysical Prospecting, 60, 681-695.

Dai, W., and Schuster, G. T., 2009, Least-squares migration of simultaneous data with a deblurring filter: 79th Annual International Meeting, SEG, Expanded Abstracts, 2990–2994.

Dai, W., and Schuster, G. T., 2013, Plane-wave leastsquares reverse time migration: Geophysics, 78(4), S165 -S177.

Fomel, S., 2002, Applications of plane-wave destruction filters: Geophysics, 67(6), 1946-1960.

Fomel, S., 2007, Shaping regularization in geophysical estimation problems: Geophysics, 72(2), R29–R36.

Fomel, S., 2010, Predictive painting of 3D seismic volumes: Geophysics, 75(4), A25-A30.

Hou, J., and Symes, W. W., 2015, Accelerating extended least-squares migration with weighted conjugate gradient iteration: 85th Annual International Meeting, SEG, Expanded Abstracts, 4243–4248.

Huang, J. P., Li, C., Li, Q. Y., et al., 2015, Least-squares reverse time migration with static plane-wave encoding: Chinese J. Geophys. (in Chinese), 58(6), 2046-2056.

Huang, J. P., Xue, Z. G., Bu, C. C., et al., 2014, The study of least-squares migration method based on split-step DSR: Journal of Jilin University, Earth Science Edition, 44(1), 369-374.

Huang, Y., and Schuster, G. T., 2012, Multisource leastsquares migration of marine streamer data with frequency-division encoding: Geophysical Prospecting, 60, 663–680.

Kuehl, H., and Sacchi, M. D., 2003, Least-squares waveequation migration for AVP/AVA inversion: Geophysics, 68, 262–273.

Lailly, P., 1983, The seismic inverse problem as a sequence of before stack migrations: Conference on Inverse Scattering: Theory and Application, Society for Industrial and Applied Mathematics, Philadelphia, PA, 15(2), 206-220.

Lambare, G., Virieus, J., Madariaga, R., et al., 1992, Iterative Asymptotic Inversion in the Acoustic Approximation: Geophysics, 57, 1138-1154.

Li, Z. C., Guo, Z. B., and Tian, K., 2014, Least-squares reverse time migration in visco-acoustic medium: Chinese J. Geophys. (in Chinese), 57(1), 214-228.

Liu, Y., Fomel, S., and Liu, G., 2010, Nonlinear structureenhancing filtering using plane-wave prediction: Geophysical Prospecting, 58, 415–427.

Liu, Y. J., Li, Z. C., Wu, D., et al., 2013a, The research on local slope constrained least-squares migration: Chinese J. Geophys. (in Chinese), 56(3), 1003-1011.

Liu, Y, J., Symes, W. W., and Li, Z. C., 2013b, Multisource least-squares extended reverse time migration with preconditioning guided gradient method: 83rd Annual International Meeting, SEG, Expanded Abstracts, 3709-3715.

Liu, Y. S., Teng, J. W., Xu, T., et al., 2016, An efficient step-length formula for correlative least-squares reverse time migration: Geophysics, 81(4), S221-S238.

Liu, Y., Wang, D., Liu, C., et al., 2014, Structure-oriented filtering and fault detection based on nonstationary similarity: Chinese J. Geophys. (in Chinese), 57(4), 1177 -1187.

Lu, X. T., Han, L. G., Zhang, P., et al., 2015, Direct migration method of multi-source blended data based on total variation: Chinese J. Geophys. (in Chinese), 58(9), 3335-3345.

McMechan, G. A., 1983, Migration by extrapolation of time-dependent boundary values: Geophysical Prospecting, 31(3), 413–420.

Nemeth, T., Wu, C., and Schuster, G.T., 1999, Least-squares migration of incomplete reflection data: Geophysics, 64(1), 208–221.

Romero, L. A., Ghiglia, D. C., Ober, C. C., and Morton, S. A., 2000, Phase encoding of shot records in prestack migration: Geophysics, 65, 426–436.

Schuster, G. T., Wang, X., Huang, Y., Dai, W., et al., 2011, Theory of multisource crosstalk reduction by phaseencoded statics: Geophysical Journal International, 184(3), 1289–1303.

Tang, Y., and Biondi, B., 2009, Least-squares migration inversion of blended data: 79th Annual International Meeting, SEG, Expanded Abstracts, 2859–2863.

Wang, J., Kuehl, H., and Sacchi, M. D., 2005, Highresolution wave-equation AVA imaging: Algorithm and tests with a data set from the Western Canadian Sedimentary Basin: Geophysics, 70(5), S91–S99.

Wang, J., and Sacchi, M. D., 2009, Structure constrained least-squares migration. 79th Annual International Meeting, SEG, Expanded Abstracts, 2763–2767.

Wang, H. C., Chen, S. C., Chen, G. X., et al., 2014. Migration methods for blended seismic data of multisource: Chinese J. Geophys. (in Chinese), 57(3), 918-931.

Wang, H. C., Chen, S. C., Zhang, B., et al., 2013. Separation method for multi-source blended seismic data: Applied Geophysics, 10(3), 251-264.

Whitmore, N. D., 1983, Iterative depth migration by backward time propagation: 53rd Annual International Meeting, SEG, Expanded Abstracts, 382–385.

Xue, Z., Chen, Y., Fomel, S., et al., 2014, Imaging incomplete data and simultaneous-source data using least-squares reverse-time migration with shaping regularization: 84th Annual International Meeting, SEG, Expanded Abstracts, 3991–3996.

Xue, Z., Chen, Y., Fomel, S., et al, 2016, Seismic imaging of incomplete data and simultaneous-source data using least-squares reverse time migration with shaping regularization: Geophysics, 81(1), S11–S20.

Xue, Z., Fomel, S., and Sun, J., 2015, RTM interpolation using time-shift gathers: 85th Annual International Meeting, SEG, Expanded Abstracts, 2145–2148.

Zhang, Y., Duan, L., and Xie, Y., 2013, A stable and practical implementation of least-squares reverse time migration: 83rd Annual International Meeting, SEG, Expanded Abstracts, 3716-3720.

Zhang, Y., Sun, J., and Gray, S., 2007, Reverse-time migration: Amplitude and implementation issues: 77th Annual International Meeting, SEG, Expanded Abstracts, 2145–2148.

Fan Jing-Wen, received his B.Sc. from the School of Geosciences, China University of Petroleum (East China) in 2014. Presently, he is pursuing a M.Sc. in the China University of Petroleum (east China). His main research interests are seismic data denoising and least-squares migration. Email: 892872138@qq.com

Manuscript received by the Editor May 8, 2016; revised manuscript received September 17, 2016.

*This work was supported by the National Natural Science Foundation of China (Nos. 41374122 and 41504100).

1. School of Geosciences, China University of Petroleum, Qingdao 266580, China.

2. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China.

3. CNOOC China Limited, Tianjin Branch, Tianjin 300452, China.

♦Corresponding author: Zhang Kai (Email: zhksam@163.com)

© 2016 The Editorial Department of APPLIED GEOPHYSICS. All rights reserved.