3D modeling of geological anomalies based on segmentation of multiattribute fusion*

Liu Zhi-Ning, Song Cheng-Yun, Li Zhi-Yong, Cai Han-Peng, Yao Xing-Miao, and Hu Guang-Min♦

3D modeling of geological anomalies based on segmentation of multiattribute fusion*

Liu Zhi-Ning1, Song Cheng-Yun1, Li Zhi-Yong1, Cai Han-Peng2, Yao Xing-Miao2, and Hu Guang-Min♦1

3D modeling of geological bodies based on 3D seismic data is used to define the shape and volume of the bodies, which then can be directly applied to reservoir prediction, reserve estimation, and exploration. However, multiattributes are not effectively used in 3D modeling. To solve this problem, we propose a novel method for building of 3D model of geological anomalies based on the segmentation of multiattribute fusion. First, we divide the seismic attributes into edge- and region-based seismic attributes. Then, the segmentation model incorporating the edge- and region-based models is constructed within the levelsetbased framework. Finally, the marching cubes algorithm is adopted to extract the zero level set based on the segmentation results and build the 3D model of the geological anomaly. Combining the edge-and region-based attributes to build the segmentation model, we satisfy the independence requirement and avoid the problem of insufficient data of single seismic attribute in capturing the boundaries of geological anomalies. We apply the proposed method to seismic data from the Sichuan Basin in southwestern China and obtain 3D models of caves and channels. Compared with 3D models obtained based on single seismic attributes, the results are better agreement with reality.

Geological anomaly, multiattributes, fusion, segmentation, 3D modeling

Introduction

Three-dimensional (3D) modeling of geological anomalies (e.g., Weng, 2013) allows for the threedimensional spatial interpretation of geological bodies. In oil and gas exploration, 3D seismic data are used for that purpose.

The 3D modeling of geological anomalies comprises the segmentation and surface reconstruction of the anomaly. The commonest and easiest way to divide a geological anomaly is thresholding (Love and Simaan, 1985). Hanning and Pisinger (2002) published a solution for selecting the proper threshold. Hale and Emanuel (2003) first applied the normalized cuts image segmentation method to look for clusters of pixels with similar intensity. Lomask et al. (2004) proposed to extract the boundaries of salt bodies using the normalized cuts image segmentation method. Lomask et al. (2006, 2007) modified this method for processing and interpreting 3Dseismic data. Kadlec (2009) proposed a curvature-guided level set method for channel segmentation and used implicit surfaces for the surface representation instead of explicit surfaces because for the latter’s difficulty to handle topological changes. For accurate segmentation, Halpert et al. (2009) introduced the modified normalized cuts method by integrating multiple seismic attributes. To improve the efficiency of the normalized cuts method, Halpert et al. (2014) proposed to track the boundaries of salt bodies using the pairwise region comparison (PRC) for semiautomatic segmentation.To reconstruct the surfaces of geological anomalies, Frank et al. (2007) proposed to construct the implicit surface field to represent targets using discrete smooth interpolation (DSI) and reconstruct the surface of horizons and salt bodies. To more precisely delineate geological structures, Caumon et al. (2009) combined Delaunay triangulation and DSI to build 3D models of faults and horizons. Hale (2013) introduced a method based on crease surfaces and used this method to reconstruct fault surfaces.

In summary, existing methods mostly have the following shortcomings. (1) In the process of segmentation, the surface reconstruction is not considered (Hale and Emanuel, 2003; Lomask et al., 2007; Halpert et al., 2009, 2014). The segmentation results are scattered points that do not contain any information about the shape or topology of the targets. Moreover, geological anomalies often have complex shapes and topologies, which make the surface reconstruction based on scattered points difficult. (2) Segmentation is limited to single seismic attribute (Hale and Emanuel, 2003; Kadlec, 2009) and, thus, it is hard to obtain the exact shape or capture all the features of the target. (3) The analysis of multiple seismic attributes only focuses on the direct combination of segmentation results obtained from each of the seismic attributes (Lomask et al., 2007; Halpert et al., 2009, 2014) and ignores the characteristics of the different seismic attributes. Besides, these methods do not have rules for selecting the seismic attributes or result in adaptable segmentation models to different kinds of seismic attributes. (4) The application to 3D surveys is prohibitively expensive because of computational complexity (Hale and Emanuel, 2003; Lomask et al., 2007; Halpert et al., 2009). For example, the normalized cuts method requires the establishment of large-scale matrices, whose size is the squared number of voxels in the data volume and the calculation of eigenvectors, which is infeasible for very large 3D volumes.

To solve the above-mentioned problems, we present a multiattribute fusion segmentation method for building 3D models of geological anomalies. We build the segmentation model based on the level set method, which incorporates the segmentation with the surface reconstruction and decreases the difficulty of reconstructing the surface results owing to the implicit surface representation of geological anomalies by the level set method. In addition, we divide the seismic attributes into edge- and region-based seismic attributes, which satisfy the independence requirement (Barnes, 2000). Finally, we construct segmentation models corresponding to each kind of seismic attributes to take advantage of the information they contain.

Segmentation method based on level sets

The level set method is used for motion tracking, surface reconstruction, and image segmentation; it tracks the dynamic evolution of boundaries and is expressed as the deformation of implicit surfaces. A level set of function f is a set of form f (x) = c (c is a constant). In particular, if c = 0, the corresponding level set is called zero level set (Osher and Sethian, 1988). It represents the contours (cut boundary) as the zero level of the level set function. All points on the evolution surface S are expressed implicitly (Osher and Sethian, 1988)

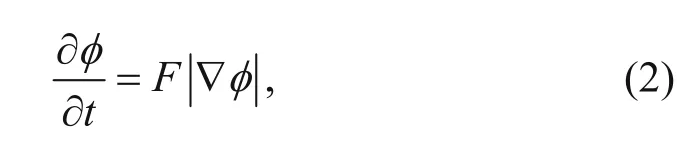
where F is the normal velocity component that guides the motion of the contour, t is the time variable, and∇ is the gradient operator. This PDE is also called the level set evolution equation. The zero level set is able to stop at the boundary of the target and completes the segmentation with the help of a carefully designed function F, which is typically derived from the gradient flow that minimizes an energy functional (Li et al., 2010).

To obtain the 3D model of a geological body, we establish the level set equation based on selected seismic attributes and build the 3D model from the segmentation results. The flowchart for this is shown in Figure 1. The selection of seismic attributes and corresponding segmentation model are the two factors that most affect the performance.

Fig.1 Workflow for the proposed method.

Segmentation model based on seismic attributes

A valid seismic attribute is sensitive to geological features and thereby enables their recognition and subsequent interpretation. Coherence, curvature, dip, and azimuth are commonly used seismic attributes For instance, Gao (2003) used texture homogeneity to analyze channels in turbidites because the texture attributes can show the internal facies variations within channel systems. The recognition of these features assist in understanding the spatial distribution of the channels.

Using a single seismic attribute is often insufficient to obtain the appropriate segmentation results. Considering the analysis of caves, as an example, Figure 2 shows two timeslices (t = t1, t2) of the coherence and texture homogeneity volumes calculated based on post stack data from Sichuan Basin in southwestern China. We hardly recognize the cave boundaries based on the slice of the coherence volume in Figure 2a. Likewise, it is challenging to precisely extract the boundaries using image segmentation algorithms (Kaldec, 2009) based on coherence, especially, when the right part of the cave is easy confused with the background. Nevertheless, the timeslice of the texture homogeneity volume in Figure 2b shows the cave clearly. Based on the texture homogeneity, the cave boundaries can be delineated with high confidence. On the contrary, in Figures 2c and 2d, the coherence volume clearly shows the boundary. Not much useful information is observed from the timeslice of the texture homogeneity volume.

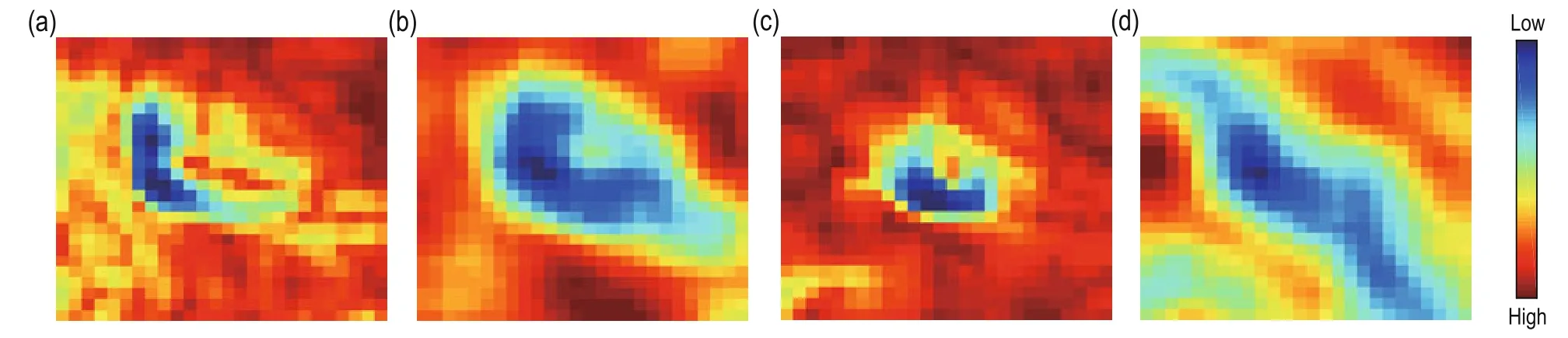
Fig.2 Timeslices of the coherence volume ((a,c) and texture homogeneity volume (b,d) at t = t1 and t = t2, respectively.

It is necessary to simultaneously use multiple attributes for the segmentation of geological bodies. In selecting suitable attributes, Barnes (2000) advised to use attributes that are independent of each other. Chopra and Marfurt (2005) also suggested that each attribute should capture only one type of physical property or feature, which can be combined with geostatistics or other multiattributes analysis tools. In addition, the level set method for image segmentation can be divided into region- and edge-based models (Li et al., 2010) depending on the information used in segmentation. Inspired by these ideas, we also categorize the seismic attributes into edge- and region-based seismic attributes. This classification is based primarily on seismic attributes that delineate the features of internal regions or boundaries that correspond to positions with abnormal values on the seismic attribute volume.

Edge-based seismic attributes typically have abnormal values, such as coherence, similarity, and variance volume, near the boundaries of geological bodies. However, these seismic attributes are quite sensitive to noise and the weakly defined geological anomalies,which leads to serious boundary leakage (Figure 8a) and significantly affects the segmentation results. Regionbased seismic attributes focus on the pattern within the internal regions of geological anomalies, such as texture attributes, energy attributes, and the root-mean-square amplitude. The calculation of region-based seismic attributes is often based on statistics and relatively large window sizes; therefore, region-based seismic attributes are more robust to noise. However, this creates another problem, poor performance in describing the details in region-based seismic attributes, as they change mildly at the vicinity of boundaries (Figure 2b). To overcome the weaknesses of the two kinds of seismic attributes, we establish a robust and combinational segmentation model that integrates the two kinds of seismic attributes to avoid boundary leakage and blurring. After selecting the appropriate seismic attributes, we need to build an image segmentation model that incorporates the regionand edge-based models within the framework of the level set method.

Level set segmentation model based on multiple seismic attributes

The proper level set equation, which is derived from the gradient flow that minimizes the energy functional, is necessary to combine the two kinds of seismic attributes and to divide the geological body using the seismic attributes volume.

ε φ is

where λ ＞ 0, α ＞ 0, and μ ＞ 0 are hyperparameters that need to be determined before segmentation. They represent the weights of L(φ), A(φ), and Rp(φ) in functional ε(φ), respectively. L(φ) and A(φ) are (Li et al., 2010)

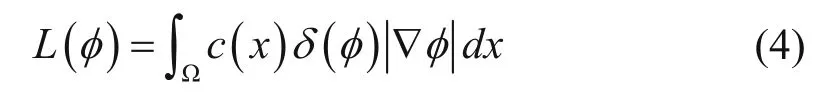
and

where δ and H are the Dirac delta function and Heaviside step function, respectively. The regionrepresents the space outside the geological anomaly and h1is the mean of h(x) in region Ω1. Regionrepresents the interior of the geological anomaly and h2is the mean of h(x) in region Ω2.

Using the Dirac delta function δ, L(φ) computes the surface integral of function c along the zero level set. c represents the edge-based seismic attributes volume, and c(x) represents the value of some point on the seismic attributes volume. We assume that c(x) is smaller near the boundary of the geological anomaly; otherwise, c(x) can be transformed by flipping the sign or taking the reciprocal. Following the gradient descent flow of L( φ), the zero level set is driven to the region with low coherence, which is the boundary of the geological anomaly with the highest probability.

h represents the region-based seismic attributes volume and h(x) represents the value of some point on the seismic attributes volume. The definition of A(φ) is based on the Chan–Vese model (Chan and Vese, 2001). To minimize A(φ), the zero level set will stop evolving when the segmentation is maximum between cluster variances; that is, the segmentation result shows the greatest differences in the region-based features between the interior and the exterior and, therefore, the boundary is likely to match the boundary of the geological anomaly.

The gradient descent flows of L(φ) and A(φ) both guide the zero level set to locate the boundary of the geological anomaly, and produce similar results based on different information. As shown in Figures 2a and 2b, there are parts of the boundary with high coherence, which are similar to the background, and this will result in low gradient descent flow and make the zero level set to stop at the wrong position. Texture homogeneity clearly delineates the cave boundaries and, under the guidance of A(φ), the zero level set will continue to move until it reaches the desired position; thus, preventing boundary leakage problems. The opposite situation is seen in Figures 2c and 2d. Divergent texture features, which reduce the effectiveness of A(φ), often lead to poor segmentation. Owing to the gradient descent flow of L(φ), the zero level set is in the state of motion until it achieves balance between A(φ) and L(φ). The segmentation will yield more appropriate boundary choices for the cave.

Rp(φ) is the level set regularization term that ensures the stable evolution of the level set (Li et al., 2010)

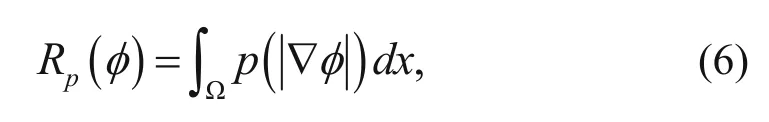
where p is the energy density functionBecause the selection of p is tricky, in this study, we choose the double-well potential function proposed by Li et al. (2010)

The energy functional ε(φ) can be minimized using the gradient descent method and by solving the gradient flow

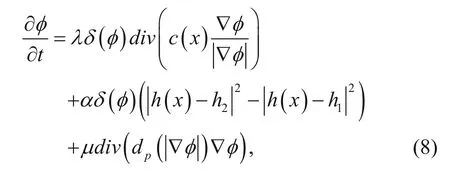
where div(·) is the divergence operator, function dpis defined asand

hiare updated after every iteration of equation (8).

Compared with equation (2), we find that equation (8) is the evolution of the level set equation of the segmentation model; therefore, the motion of the zero level set depends on the gradient descent flow of ε(φ) (Li et al., 2010). After several iterations of updating φ, following the gradient flow, we obtain the signed distance function of the boundary of the geological anomaly.

Compared with the normalized cuts method, the segmentation based on the level set method only needs to update the data volume with size equal to the input data in every iteration. The computational cost of updating is greatly reduced by adopting a narrowband implementation (Li et al., 2010). The level set method is naturally compatible with the parallel implementation (Kaldec, 2009). Using these techniques, real-time interactive interpretation becomes feasible.

In addition, prior information input by users can be easily combined with the proposed segmentation model. For example, the value of c0of the edge-based seismic attributes is set by the user, in advance, and A(φ) can be rewritten aswhich is similar to the model proposed by Kadlec (2009). However, the latter only starts to work after the parameter c0is given. On the contrary, the proposed model can automatically extract the geological anomaly without user input and A(φ) is added to solve the boundary leakage problem. Clearly, the proposed method has much wider applicability and higher accuracy than Kadlec’s method.

Similarly, if the mean of region-based attributes in the internal region of the geological anomaly is predefined, A(φ) can be rewritten as

where h1is defined as above.

In addition, the proposed method can be applied to combine seismic attributes

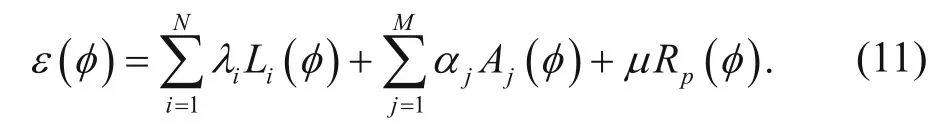
The minimization of the functional ε(φ) leads to the fusion of N edge-based seismic attributes and M regionbased seismic attributes.

Surface reconstruction based on the level set segmentation

After segmentation, the position in space of the geological anomaly is obtained, and we reconstruct the surface based on the scattered points given by the segmentation. By using a triangular mesh, we can visualize it, which is the last step of the workflow in Figure 1. The method proposed by Frank et al. (2007) can be adopted to reconstruct the surface. The triangular mesh can be constructed based on the isosurface of the implicit surface field given by the scattered points. In this study, the level set function φ, which is also a signed distance function, implicitly represents the geological anomaly and the zero level is corresponding to the boundary. We adopt the marching cubes algorithm to extract the zero level set to complete the surface reconstruction (Lorensen et al., 1987). Based on the assumption that the level set function is linear locally, the marching cubes algorithm takes eight neighboring locations at a time and then determines the polygon needed to delineate the isosurface that passes through this cube. These polygons are finally fused into the boundaryof the geological anomaly. A simple illustration of the algorithm is shown in Figure 3. After extracting the isosurface in all cubes, the 3D model of the geological anomaly can be obtained. Figures 4 and 9 show the triangular mesh of the caves and channel, respectively. With the 3D model of the geologicalanomaly and calculating the local illumination model, a computer can easily realize the 3D visualization, shown in Figures 5 and 10.

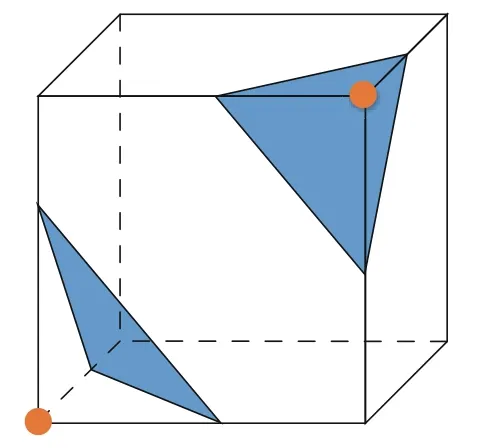
Fig.3 Extraction of the triangular mesh in the marching cubes algorithm; the 256 origins can be reduced to 15 based on the rotational and reflective symmetry. The vertices (brown) suggest that the scalar value of the vertex is lower (or higher) than isovalue and scalar value of the rest vertex is higher (or lower) than the isovalue.

The surface reconstruction based on segmentation, which is obtained within the level set framework, transforms the original task into simple isosurface extraction. Compared with traditional methods based on point cloud, the proposed method greatly simplifies the 3D modeling of a geological anomaly. Moreover, the proposed method incorporates the information on the shape and topology, such as the connectivity among geological anomalies obtained during the segmentation, into the surface reconstruction of the segmentation results based on the level set method in the signed distance field, which indicates the relative position to the boundary using the sign. If we ignore this information and just consider the segmentation results as point cloud, extra work is needed to construct the distance field related to the boundary of the geological anomaly (Zhao et al., 2001), which is a low-efficiency method.

Application

We apply the proposed method to two seismic datasets from Sichuan Basin in China. For edge-based seismic attributes, we choose coherence for extracting caves and channels because it is sensitive to the lateral variations of the waveforms and can easily recognize the boundaries of geological anomalies, which makes coherence suitable for extracting most geological anomalies (Wen et al., 2011). The selection of region-based seismic attributes depends on the characteristics of the geological anomalies. Next, we describe in detail the 3D modeling of the caves and channel.

Cave extraction

We test the proposed method on postseismic data from Sichuan Basin and build a 3D model of caves. The size of the data volume is 250 × 250 × 100. We choose coherence and texture homogeneity to represent the edge- and region-based seismic attributes, respectively. We choose texture homogeneity because the texture inside the cave differs from the one externally to the cave (Figure 2b).

After generating the signed distance field in the space based on the initial surface, we iteratively optimize the objective function once we have selected the three hyperparameters. We take λ = 7, α = 9, μ = 0.1, and the step of iteration Δt = 1. After several iterations, we obtain the segmentation and the 3D model of the caves by extracting the isosurface from the signed distance field using the marching cubes algorithm. The results are shown in Figures 4 and 5. Figure 6 shows the boundary of the cave on the corresponding seismic section and time slice. From the figures, we can conclude that the cave-like regions are precisely identified.

Fig.4 Triangle mesh of a cave.

Figure 7 shows the cave boundary on the timeslice shown in Figure 2. From Figure 7, we observe that the segmentation results benefit from the combination of coherence and texture attributes compared with thesegmentation results based on a single seismic attribute, which is shown in Figure 8. We thus conclude that the proposed method improves the segmentation accuracy.

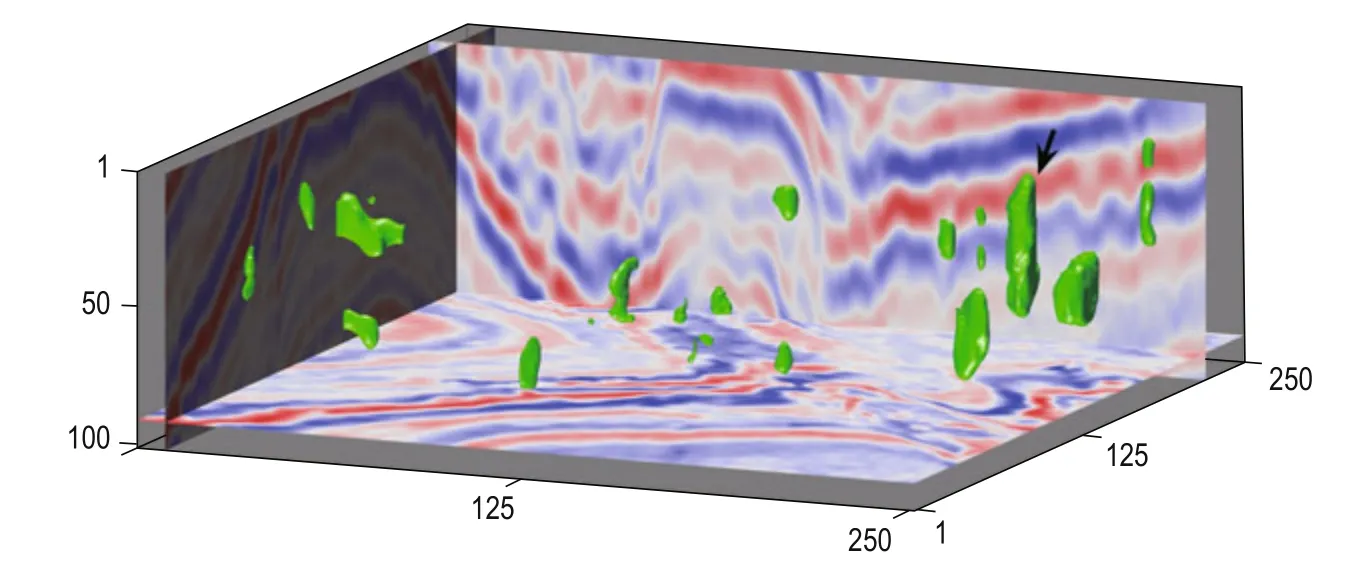
Fig.5 3D model of caves obtained with the proposed method. The timeslices in Figures 2, 6, 7 and 8 are all from the cave indicated by the black arrow.

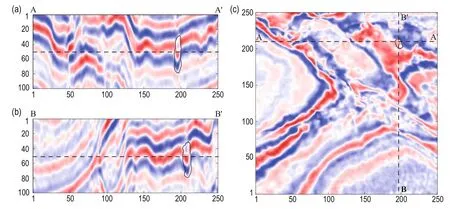
Fig.6 The cave boundary (black solid curve) shown in the seismic section and timeslice. (a) Seismic section along AA’ in (c); (b)seismic section along BB’ in (c); and (c)timeslice of seismic data at t = 50.

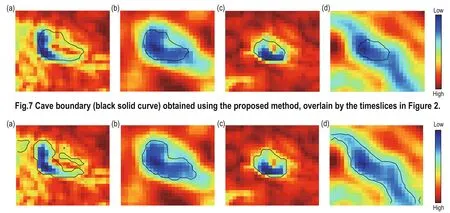
Fig.8 Segmentation results based on the texture homogeneity only, overlain by Figure 2a (a) and Figure 2c (c). Segmentation results based on coherence only, overlain by Figure 2b (b) and Figure 2d (d).

Channel Extraction

Energy (Zhang et al., 2011) and curvature are both able to capture the regional features of channels because channels have features with high amplitude and significant curvature (Kaldec et al., 2008). In this study, we choose the combination of coherence and energy to build the 3D model of a channel. The only difference between the 3D modeling of the cave and the channel is that we choose different combinations of seismic attributes. The size of data volume is 150 × 100 × 25. After several iterations, we obtain the 3D model in Figures 9 and 10. Figure 11 shows the boundary of the channel on the corresponding seismic section and timeslice, and we conclude that the channel characteristics are well identified.

Fig.9 Triangle mesh of channel.

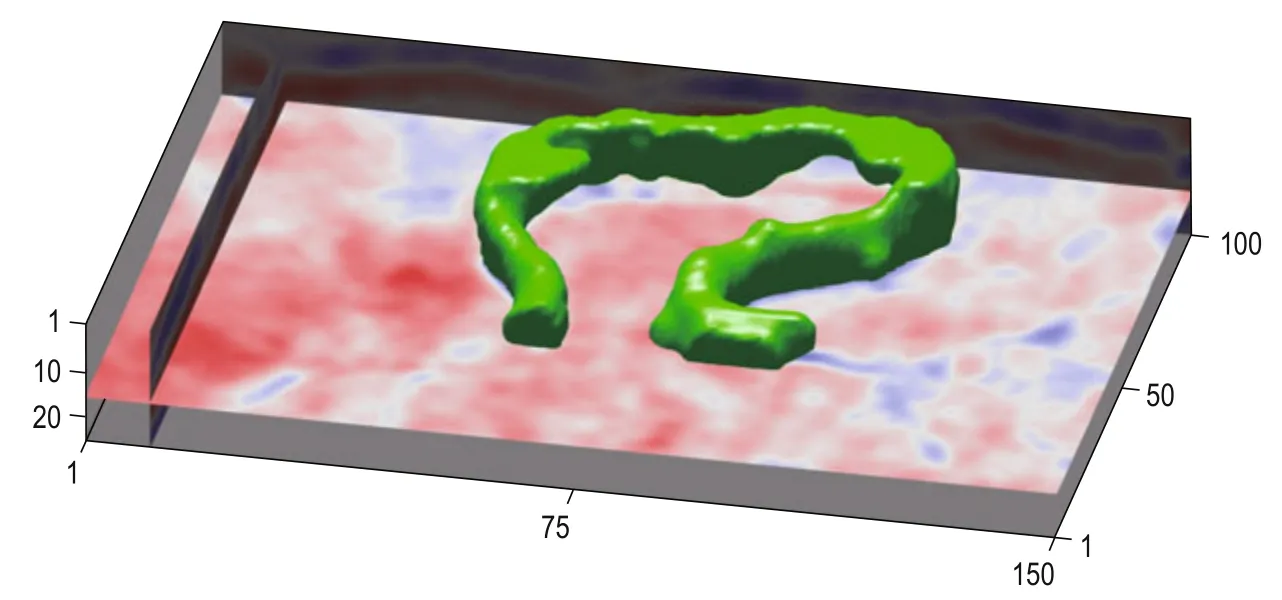
Fig.10 3D model of channel (visualized with illumination) obtained using the proposed method.

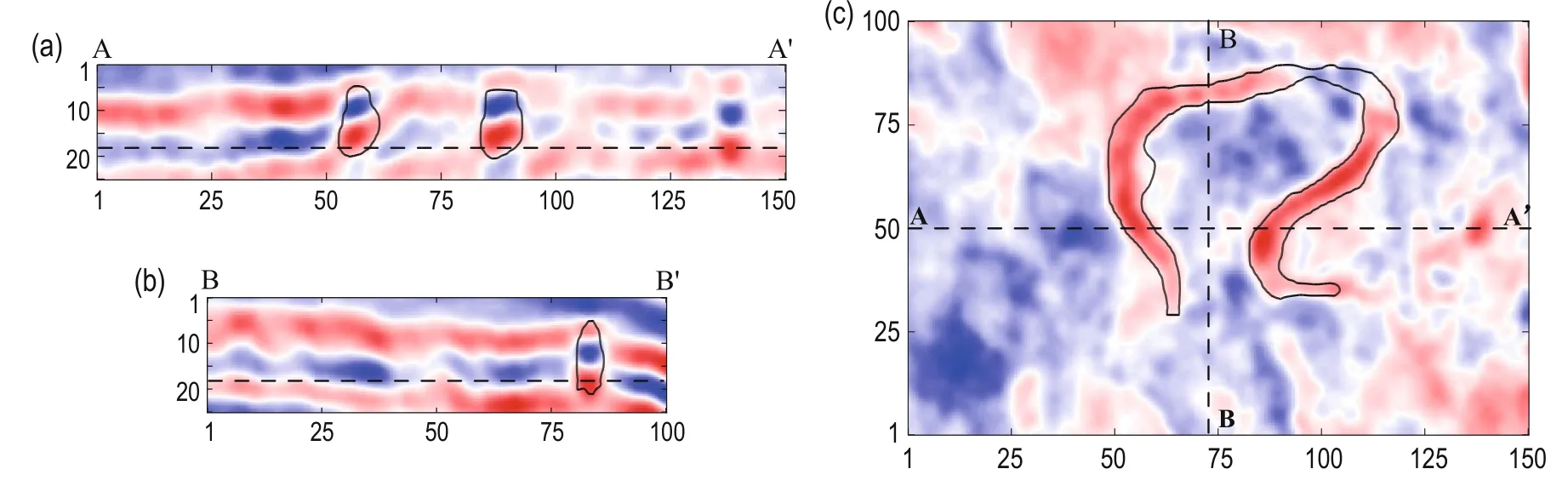
Fig.11 The boundary (black solid curve) of the channel in the seismic section and timeslice.

The reliability of the results can also be verified by the 2D image generated by mapping the 3D segmentation result to the timeslice, shown in Figure 12. In Figure 12a, the region marked by the blue arrow has a serious boundary leakage problem if the channel extraction is only based on low-coherence features, which correspond to the black parts. In Figure 12b, even though the outlying region marked by the yellow arrow has similar values with the internal region of the channel, this is not seen in the final segmentation results. We thus conclude that the combination of the two seismic attributes improves the segmentation accuracy.

Fig.12 Segmentation (region marked by the red curve) at one time slice. Background is time slice from coherence volume (a) and energy volume (b), respectively. The arrows mark the position with segmentation errors when using a single seismic attribute.

Conclusions

To build precise 3D models of geological anomalies, a novel method of constructing 3D models of geological anomalies based on the segmentation of combined attributes is proposed. First, we divide the seismic attributes into two general categories, and construct a segmentation model that incorporates multiple attributes within the level set-based framework. Finally, we adopt the marching cubes algorithm to extract the zero levelset based on the segmentation results and build 3D models of geological anomalies. The experimental results suggest the following.

A single seismic attribute is insufficient to extract 3D models of geological anomalies, which result in inconsistencies between segmentation results and the boundaries of the geological anomaly. The resulting 3D model is not reliable because of its poor performance in characterizing the target. However, reasonable combinations of multiple seismic attributes can complement each other. Therefore, it is necessary to analyze multiple attributes when constructing 3D models of geological anomalies.

The 3D modeling of geological bodies based on the combination of edge- and region-based seismic attributes is feasible. The fusion of multiple attributes satisfies the independence requirements and is closely associated with classical segmentation models.

The analysis of multiple attributes, segmentation, and surface reconstruction are combined within the framework of the level set method. After segmentation, the level set method uses implicit surfaces to represent the segmentation results, while preserving the topology of the geological anomaly. This simplifies the surface reconstruction based on the segmentation results and improves the quality of the reconstructed surface. Using the level set method, we can directly transform 3D seismic data to 3D models without point cloud-based surface reconstruction. Compared with the normalized cuts method, the segmentation-based level set method is more suitable for 3D modeling of geological anomalies.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (No.41604107) and the Scientific Research Staring Foundation of University of Electronic Science and Technology of China (Grant No. ZYGX2015KYQD049). The authors wish to thanks to the Editor and reviewers He Zhenhua, Chen Tiansheng and Cai Xiling for their comments.

Barnes, A. E., 2000, Attributes for automated seismic facies analysis: 70th Annual International Meeting, SEG, Expanded Abstracts, 553–556.

Caumon, G., Collon-Drouaillet, P., De Veslud, C. L. C., and Sausse, J., 2009, Surface-based 3D modeling of geological structures: Mathematical Geosciences, 41(8), 927-945.

Chan, T. F., and Vese, L., 2001, Active contours without edges: Image processing, IEEE transactions on, 10(2), 266-277.

Chopra, S., and Marfurt, K. J., 2005, Seismic attributes—A historical perspective: Geophysics, 70(5), 3-28.

Frank, T., Tertois, A. L., and Mallet, J. L., 2007, 3D-reconstruction of complex geological interfaces from irregularly distributed and noisy point data: Computers & Geosciences, 33(7), 932-943.

Gao, D., 2003, Volume texture extraction for 3D seismic visualization and interpretation: Geophysics, 68(4), 1294 -1302.

Hale, D., and Emanuel, J., 2003, Seismic interpretation using global image segmentation: 73rd Annual International Meeting, SEG, Expanded Abstracts, 2410-2413.

Hale, D., 2013, Methods to compute fault images, extract fault surfaces, and estimate fault throws from 3D seismic images: Geophysics, 78(2), 33-43.

Halpert, A. D., Clapp, R. G., and Biondi, B., 2009, Seismic image segmentation with multiple attributes: 79th Annual International Meeting, SEG, Expanded Abstracts, 3700-3704.

Halpert, A. D., Clapp, R. G., and Biondi, B., 2014, Salt delineation via interpreter-guided 3D seismic image segmentation: Interpretation, 2(2), 79-88.

Hanning, T., and Pisinger, G., 2002, A pixel-based segmentation algorithm of color images by N-levelfitting: 5th IASTED International Conference on Computer Graphics and Imaging (Honolulu, Hawaii), 138-144.

Kadlec, B. J., Dorn, G. A., and Tufo, H. M., 2008, Confidence and curvature-guided level sets for channel segmentation: 78th Annual International Meeting, SEG, Expanded Abstracts, 879-883.

Kadlec, B. J., 2009, Interactive GPU-based visualization and structure analysis of three-dimensional implicit surfaces for seismic interpretation: PhD Thesis, University of Colorado, Colorado.

Li, C., Xu, C., Gui, C., and Fox, M. D., 2010, Distance regularized level set evolution and its application to image segmentation: Image Processing, IEEE Transactions on, 19(12), 3243-3254.

Lomask, J., Biondi, B., and Shragge, J., 2004, Image segmentation for tracking salt boundaries: 74th Annual International Meeting, SEG, Expanded Abstracts, 2443–2446.

Lomask, J., Clapp, R. G., and Biondi, B., 2006, Parallel implementation of image segmentation for tracking 3D salt boundaries: 68th Annual Conference and Exhibition, EAGE, Extended Abstracts, 1402-1405.

Lomask, J., Clapp, R. G., and Biondi, B., 2007, Application of image segmentation to tracking 3D salt boundaries: Geophysics, 72(4), 47-56.

Lorensen, W. E., and Cline, H. E., 1987, Marching cubes: A high resolution 3D surface construction algorithm: ACM siggraph computer graphics, 21(4), 163–169.

Love, P. L., and Simaan, M., 1985, Segmentation of a seismic section using image processing and artificial intelligence techniques: Pattern Recognition, 18(6), 409-419.

Osher, S., and Sethian, J. A., 1988, Fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations: Journal of computational physics, 79(1), 12-49.

Wen, X., He, Z., Huang, D., and Chen, X., 2011, Highlighting display of geologic bodies based on directivity filtering: Applied Geophysics, 8(4), 355-362. Weng, Z. P., 2013, Fast Building and Refreshing Threedimensional Models of Geological Entity: PhD Thesis, China University of Geosciences, Wuhan.

Zhao, H. K., Osher, S., and Fedkiw, R., 2001, Fast surface reconstruction using the level set method: Variational and Level Set Methods in Computer Vision, Proceedings, IEEE Workshop on, 194-201.

Zhang J., Liu, Z., Zhu B, Feng, D., Zhang, M., and Zhang, X., 2011, Fluvial reservoir characterization and identification: A case study from Laohekou Oilfield: Applied Geophysics, 8(3), 181-188.

Liu Zhi-Ning received his B.Sc. in communication engineering from the University of Electronic Science and Technology of China in 2014. He is currently pursuing his doctoral degree in information and communication at the University of Electronic Science and Technologyof China. His research interests are seismic attributes and geological body segmentation. Email: liuzhiningUESTC@gmail.com

Manuscript received by the Editor November 13, 2015; revised manuscript received September 18, 2016.

*This work was supported by the National Natural Science Foundation of China (No. 41604107) and the Scientific Research Staring Foundation of University of Electronic Science and Technology of China (No. ZYGX2015KYQD049).

1. School of Communication and Information Engineering, University of Electronic and Technology of China, Chengdu 611731, China.

2. School of Resources and Environment, University of Electronic and Technology of China, Chengdu 611731, China.

♦Corresponding author: Hu Guang-Min (Email: hgm@uestc.edu.cn)

© 2016 The Editorial Department of APPLIED GEOPHYSICS. All rights reserved.