深部花岗岩巷道两帮稳定性力学模型分析

牟举文 臧传伟 徐国栋 邢宇祺 杨运琦

(1.北京交通大学土木建筑工程学院；2.山东科技大学矿业与安全工程学院；3.北京科技大学土木与环境工程学院)



深部花岗岩巷道两帮稳定性力学模型分析

牟举文1臧传伟2徐国栋3邢宇祺1杨运琦2

(1.北京交通大学土木建筑工程学院；2.山东科技大学矿业与安全工程学院；3.北京科技大学土木与环境工程学院)

依据组成花岗岩岩体矿物的解理特性，探讨了花岗岩巷道两帮层裂板结构的形成机理，并应用材料力学中的压杆稳定性原理，建立了层裂板结构稳定性近似力学模型，分析了花岗岩巷道两帮层裂板结构失稳的力学机制，提出了判断花岗岩巷道两帮稳定性的判据公式，并用ANSYS数值模拟软件的分析结果证实了判据公式的有效性，为类似围岩条件下的隧道工程提供了一定的指导作用。

花岗岩 片帮 压杆稳定性 层裂板结构 临界压力 数值模拟

随着矿山、水利水电、铁路(公路)交通隧道等工程向深部发展，片帮、岩爆作为一种深部灾害现象[1]，其发生越来越频繁。为了有效制定片帮、岩爆的防治技术措施，保证深部隧道工程的安全性，深入开展片帮、岩爆的机制研究非常必要。由于影响片帮、岩爆的因素很多，目前对片帮、岩爆的发生和破坏机制还没有很清楚的认识，对片帮、岩爆的防治措施还不够准确[2]。

通过对大量资料[3-6]分析，发现片帮、岩爆与巷道自由壁面平行裂纹的产生和发展有密切的关系,认为巷道两帮围岩存在压应力,当应力达到一定值,初始裂隙将会平行或偏向最大主应力的方向扩展，并逐渐朝压缩方向产生分叉。随着载荷增加,裂纹长度将相应增长，在裂纹达到一定长度后,自由表面的存在导致裂纹非稳定扩展,从而使裂纹长度突然增长并使岩体分裂形成薄层。左宇军等人[7]建立了洞室层裂屈曲岩爆的突变模型,得出了洞室层裂屈曲岩爆在准静态破坏条件下的演化规律。冯涛等人[8]利用扫描电镜试验对岩爆岩石板状结构形成进行了分析研究，认为岩石解理断裂存在一个明显的主断裂路径,岩爆断裂的微观机制主要是在拉伸、剪切作用下岩石发生低应力脆性断裂。苗金丽、何满潮等人[2]认为岩爆现象多发生在高应力的硬岩岩体中，并对深部高应力条件下的花岗岩片帮、岩爆过程进行实验研究,初步探讨岩爆发生机制。

本文综合上述优秀研究成果的基础上，依据组成花岗岩岩体(花岗岩)矿物的解理特性，探讨花岗岩巷道两帮层裂板结构的形成机理，并应用材料力学中的压杆稳定性原理，建立层裂板结构稳定性的近似力学模型，分析花岗岩巷道两帮层裂板结构失稳的力学机制，提出了花岗岩巷道两帮的稳定性近似判据公式，并用ANSYS数值模拟软件证实判据公式的有效性。

1 花岗岩岩体层裂板结构的形成机理

花岗岩是大陆地壳的主要组成部分，是一种岩浆在地表以下凝结形成的火成岩，属于深层侵入岩，主要组成矿物为长石、石英、黑白云母等，石英含量为10%～50%，长石含量约占总量2/3，分为正长石、斜长石(碱石灰)及微斜长石(钾碱)。在我国无论是煤矿、金属矿开采过程中还是水电站或交通隧道的建设过程中都经常遇到花岗岩[9],且在很多花岗岩类围岩中开挖巷道的工程实践中经常遇到片帮、岩爆的现象[10]。

大量工程实践表明,岩土材料的宏观工程性质在很大程度上受到其微结构系统状态或整体行为的控制,复杂的物理力学性质是其微结构特性的集中体现[11]。通过对花岗岩的矿物分析发现，组成花岗岩的矿物中正长石具有2组彼此成90°正交的解理，斜长石具有2组彼此成86°斜交的解理，云母有一组极完全解理，很容易揭开成薄片[12]。

由于开挖巷道围岩应力重新分布，巷道附近压应力集中，由于花岗岩有上述的矿物组成及解理特性，在巷帮自由壁面附近的围岩内部沿着长石解理面发生穿晶破坏，形成与壁面平行的贯穿型裂纹，使得巷道附近岩体开裂，形成板状劈裂，在近巷道壁围岩中形成岩板结构—层裂板结构。

在野外很容易看到花岗岩岩体的层裂现象(图1)，通过对花岗岩块的片帮、岩爆实验研究，利用电镜扫描试样碎片，经高倍放大后可以发现试样的微观层裂结构，见图2。

图1 花岗岩层裂宏观图

图2 花岗岩层裂微观图

2 层裂板结构稳定性的力学模型及分析

综上花岗岩巷帮层裂板的形成分析，宏观工程性质在很大程度上受到其微结构系统状态或整体行为的控制。从微分的角度来看，具有一定厚度的板状结构可以看成是由无数个细长的杆状结构组成的；从花岗岩的矿物组成及解理特性来看，层裂板是一个内部充满无数细小节理的不连续介质体，当外力达到一定程度，这种细小节理会逐渐贯通，将板状岩体划分成无数细长的杆状结构，在这种应力状态下，细长杆状结构的力学反应成为了控制整个板状岩体稳定性的主要因素。因此，通过研究花岗岩巷道两帮层裂板细长杆状结构的稳定性来讨论层裂板的稳定性具有一定的实际意义。

花岗岩巷道两帮层裂板细长杆状结构的稳定性力学模型可简化为图3所示材料力学压杆稳定性原理的力学模型,根据压杆稳定性原理可解出图中杆件所受的最大弯曲正应力[13]。

图3 压杆稳定性力学模型

设弯曲变形发生在杆件的一个主惯性平面内，抗弯刚度为EI。在杆AC和CB两段内，挠曲线的微分方程为

(1)

(2)

式中，右端第二项即表示轴向力对弯曲变形的影响，如压力F1取绝对值，因w为负值，所以轴向压力事实上是增大了弯矩的数值。

引用记号

(3)

则截面C的挠度及弯矩分别为

(4)

(5)

引用记号

(6)

则δ及Mmax可写成

(7)

(8)

以上公式中,F1为压杆轴向受力，N；F2为压杆横向受力，N；l为压杆长度，m；E为弹性模量，Pa；I为截面惯性矩，m4；c为压杆一端到横向受力点C的距离，m;M为弯矩，N·m；w为挠度，m；δ为截面C的挠度，m。

式(7)、式(8)括号外的项代表不考虑轴向力时的挠度及弯矩，圆括号内的项代表轴向力F1对挠曲及弯矩的影响。

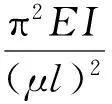
3 巷帮层裂板结构的失稳力学机制

由上述力学模型分析可知，由于围岩应力重新分布及开挖产生的动力荷载的影响，当层裂板内细长杆状结构两端的压力达到临界压力后，细长杆状结构将发生变形失稳，从而导致整个层裂板的变形失稳，最终导致整个巷帮的变形失稳。层裂板在顶底板及巷帮受力模型见图4、图5。

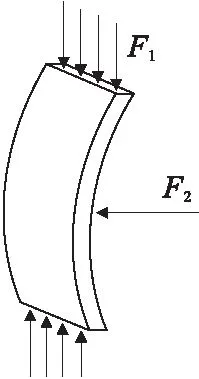
图4 板受力模型

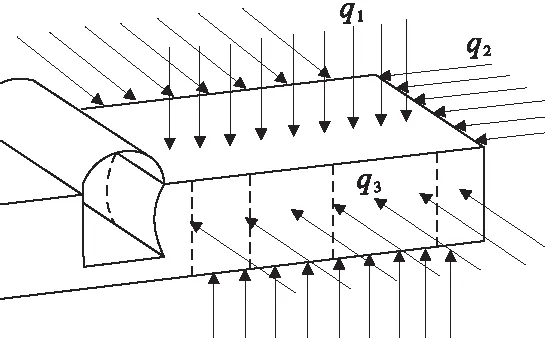
图5 巷道层裂板受力模型

4 花岗岩巷道两帮稳定性判据公式

综上层裂板失稳的力学机制可以发现，层裂板内细长杆状结构的临界压力大小直接决定了层裂板结构的稳定性大小，板内细长杆状结构的临界压力越大则层裂板的稳定性越强，反之则越弱。由于在实际隧道工程中甚至实验室内都很难得出花岗岩层裂板内细长杆状结构的具体参数，使得其临界压力计算变得十分困难。为了简化计算，提出利用花岗岩层裂板的实验数据来计算临界压力，进而评估层裂板的稳定性。

临界压力计算公式为

(9)

其中，

(10)

进一步可得判断花岗岩巷道两帮稳定性计算公式：

(11)

式中，qer为巷帮层裂板临界压力，N；E为围岩弹性模量，由实验测得，Pa；h为层裂板宽度，由实验测得，m；b为层裂板厚度，由实验测得，m；μ为长度因数，0.5～2；l为巷帮高度，m。

实际工程中，由于地质条件的复杂性，由实验室测得的花岗岩层裂板的临界压力并非唯一确定值，本文用ANSYS数值模拟软件对具有不同参数的层裂板模型进行受力分析，得出了系列可供实际隧道施工参考的结论。层裂板参数及结果分别见表1、图6。

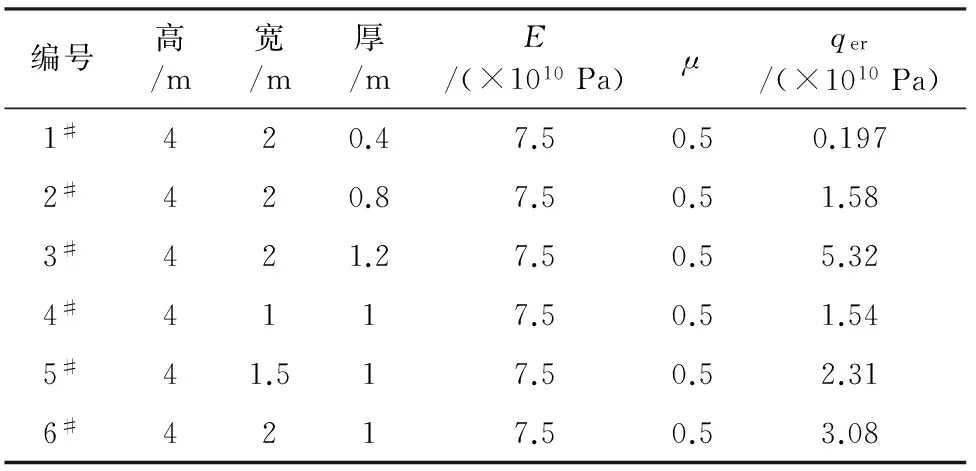
表1 ANSYS数值分析层裂板参数

由图6(a)～图6(c)可知，当层裂板的其他参数一定时，随着层裂板的厚度逐渐增大，层裂板由长杆逐渐变为短杆，临界压力增大，巷道抵抗变形的能力增强。由图6(d)～图6(f)可知，当层裂板其他参数固定时，随着层裂板宽度的增加，临界压力成正比增大，层裂板抵抗变形的能力增强，巷道更加安全。综合图6可知，当加载在层裂板两端的压力量级小于由式(11)计算出的临界压力量级时，层裂板变形很小，处于稳定状态；当加载在层裂板两端的压力量级等于由式(11)计算出的临界压力量级时，层裂板变形很大，失稳。因此，在实际隧道开挖工程施工之前可通过实验测出需开挖的花岗岩层裂板参数，预计可能因开挖造成的围岩扰动及地应力对巷帮顶底板压力的最大值，依据上述判据公式，评估在该岩体条件下实施开挖巷道两帮发生失稳的可能性，可为防治巷道片帮、岩爆提供一定的参考。

5 结 论

(1)花岗岩岩体的矿物组成及解理特性，加之受到因深部开挖而引起的强烈围岩扰动及地应力为花岗岩巷道两帮层裂板的形成提供了条件。

(2)压杆稳定性力学原理模型在花岗岩巷道两帮层裂板变形失稳分析的套用解释了在该围岩条件下巷帮失稳破坏的力学机理，并由此提出了判断花岗岩巷道两帮稳定性的近似计算公式，与ANSYS数值模拟结果相吻合，可为防治巷道片帮、岩爆提供一定的参考。

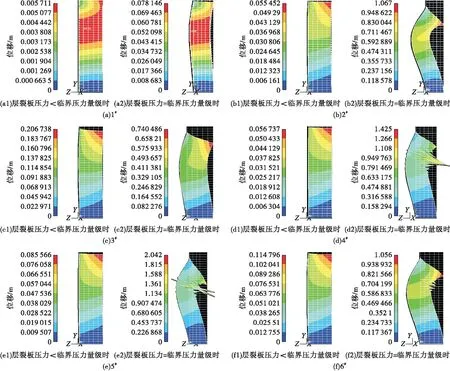
图6 ANSYS数值模拟结果

[1] 何满潮.深部的概念体系及工程评价指标[J].岩石力学与工程学报，2005，24(16)：2854-2858.

[2] 何满朝，苗金丽，李德建，等.深部花岗岩试样岩爆过程实验研究[J].岩石力学与工程学报,2007,26(5)：865-876.

[3] Kemeny J M．A model for non-linear rock deformation under compression due to sub-critical crack growth[J]．Int J Rock Mech Min Sci & Geomech Abstr，1991，28(6)：459-467．

[4] Carlson J M．Time intervals between characteristic earthquakes and correlation with smaller events：an analysis based on a mechanical model of a fault[J]．J Geophysical Res，1991，96(B3)：4255-4267．

[5] Dyskin A V，Gemmanovich L N．Model of rockburst caused by cracks growing near free surface[C]//Young ed．Rockbursts and Seismicity in Mines．NewYork，1993：169-174．

[6] 秦 昊．巷道围岩失稳机制及冲击矿压机理研究[D].徐州：中国矿业大学，2008．

[7] 左宇军,李夕兵，越国彦.洞室层裂屈曲岩爆的突变模型[J].中南大学学报：自然科学版,2005,36(2)：311-316.

[8] 冯 涛，谢学斌，潘长良，等.岩爆岩石断裂机理的电镜分析[J].中南工业大学学报,1999,30(1)：14-17.

[9] 尚嘉兰,沈乐天,赵宇辉.Bukit Timah花岗岩的动态本构关系[J].岩石力学与工程学报,1998,17(6):634-641.

[10] 赵 青.高地应力地区花岗岩强度偏低的成因研究[D].成都：成都理工大学，2009.

[11] 张华杰,孙 秋,胡 晰,等.岩土微结构试验研究综述[J].土工基础,2008,22(4):49-52.

[12] 胡绍祥，李守春.矿山地质学[M].2版.徐州：中国矿业大学出版社，2008.

[13] 刘鸿文.材料力学Ι[M].北京：高等教育出版社，2011.

2016-08-05)

牟举文(1992—)，男，硕士研究生，100044 北京市海淀区上园村3号。