教师“该出手时再出手”

文/郭晓莉

教师“该出手时再出手”

文/郭晓莉

随着新课改的不断深入，学生动手实践、自主探索、合作交流等学习方式常常体现在教学过程中，课堂气氛活跃了，学生的学习热情也提高了……师生角色初步实现了比较理想的转换。但一种奇怪的现象也随之出现了：教师在课堂上一味追求自主、合作、探究的学习方式，以至于有时放任自流，任凭学生自主而不去适时指导；有时又过于注重引导，而使学生处于被动，导致课堂上有的教师整节课无所事事，所有知识全让学生自己“探索”，而不作为；有的教师忙得团团转，但当学生真正需要时，自己却闲而无事，犹如局外人——课堂形式虽属新课程理念下的课堂形式，但教学效果却不理想。

《数学课程标准》（2011版）中明确提出：“教师是数学学习的组织者、引导者与合作者。”学生是数学学习的主人，在数学学习的过程中，教师既要当好学生学习的组织者、合作者，更要不失时机地当好学生学习的引导者。也就是说，在教学的关键环节，教师要适时引导，及时点拨，及时总结，“该出手时就出手”。

关键之处的适时引导

教师作为学生数学活动的组织者、引导者与合作者，在对教材以及教学本质的透彻理解下，要根据学生的具体情况，对教材进行再加工，创造性地设计教学过程，让学生从逐步感悟到恍然大悟。例如，在教学人教版四年级上册《求近似数》一课时，学生估数，凭借的是已有生活经验及对数感的积累，而对“近似数”这一概念的认知仍然处于模糊的状态。为什么要“四舍五入”，看似“简单”，却难以理解。因此，有位教师设计了如下教学活动：

师：一台电脑的价格大约是8000元（出示四张反扣的卡片），猜猜看，准确价格可能是多少元？

生：可能是8001、8002、7999

……

师：还有吗？这个价格好猜吗？有没有好一点的办法？

生：可以先猜千位。

师：能够有条理地思考，很棒！千位可能是几？

生：7、8。

师：为什么不可能是6、9？

生：因为它离8000太远了。

师：（出示数轴标出7000、8000、9000的位置，如下图所示）如果千位数是7，那百位呢？

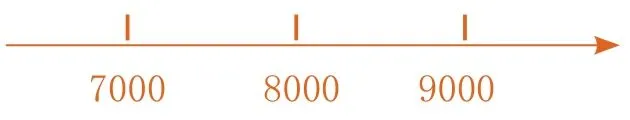
生：如果是7的话，百位可能是0。（其他学生“啊”的一声炸开了）

生：应该是9。

生：5-9。

师：为什么？

生：如果是0的话，就应该约等于7000。

生：0-4的话，近似数应该也是7000。

生：因为电脑的价格大约是8000元，如果是7040，就离8000太远了。

生：（依次在数轴上指出7500、7600、7700、7800、7900的位置）它们越来越接近8000，（在数轴上指出7400、7300、7200、7100的位置）它们越来接近7000。

师：对了，数学是讲道理的，你们说出了为什么要“四舍五入”。

【评析】在本课教学中，作为认识数的最直观的工具——数轴，呈现出了数形之间的对应关系，对学生理解概念起了很关键的作用。在数轴上探究为什么要“四舍五入”这一道理的过程中，通过学生之间、师生之间的辨析、讨论，拨云见日，掀开了近似数的“面纱”：近似数是与实际数最接近的数，它有一定的取值范围。

小组合作时的有效调控

在《倍数和因数》一课的教学时，采用了一种新的课堂结构，改变了原来固有的教学模式。所以，教师在教学时，应突出学生的主体地位，放手让学生去思考，让学生在小组合作交流中真正获得知识，提升自身能力。

下面是“怎样找一个数的因数”的教学片段。

分工合作

师：怎样找一个数的倍数学会了，那怎样找一个数的因数呢？

师：当你们阅读到这一句“你能找出36的所有因数吗？”你是直接往下看材料上的答案，还是先不看自己主动尝试的呢？

（有一部分学生是直接阅读的，也有一部分学生是先自主尝试的）

师：请举例说一说，哪些是36的因数？

师：看来，找出一个数的因数也不难。有什么好办法能够不重复、不遗漏地找出36的所有因数呢？

（出示小组活动要求：讨论：怎样才能不重复、不遗漏地找出36的所有因数？把思考的过程用算式表示出来，填写学习单。尝试：有没有其他的方法）

小组交流

第一组学生：我们是用列乘法算式的方法：1×36=36、2×18=36、3×12=36、4×9=36、6×6=36。因为两个“6”相同，我们只要写一个“6”，36的两个因数有1、2、3、4、6、9、12、18、36。

师：听了他们的汇报，你还有什么想说的？

生：我觉得写出一个乘法算式，我们就可以找到36的两个因数。这样一对一对地找，比较方便。

生：我补充一下，如果两个数相同，比如“6×6=36”，那我们只能找到36的一个因数是“6”。

师：刚才两位同学，一个总结得好，一个补充得好。除了这种方法外，还有没有其他的方法？

第二组学生：我们用的是列除法算式的方法，36÷1=36、36÷2=18、36÷3=12、36÷4=9、36÷6=6。36的因数有1、2、3、4、6、9、12、18、36。

师：两组同学，一乘一除，方法虽有所不同，但也有一些是相同的。

生：他们都是一对一对找的。

生：当两个因数相同时，我们只要写一个就行了。

生：在写出36的所有因数时，都是按从小到大的顺序依次写的。

自主尝试

师：请大家在草稿本上直接写出15、16的所有因数。

（学生汇报）（课件出示：36的因数有1、2、3、4、6、9、12、18、36。15的因数有1、3、5、15。16的因数有1、2、4、8、16。）

我思考

观察上面的例子：这三个数的因数有些什么共同的特点？

师：刚才我们是从哪三个方面来概括一个数的倍数的特点的？那一个数的因数又有什么特点呢？

生：一个数的最小的因数是1，最大的因数是它本身。一个数的因数的个数是有限的。

（根据学生回答，完成板书：因数最小1；最大它本身；个数有限）

【评析】这一片段诠释出一种新型的教学设计观。从“知识”层面看，有些知识是不需要学生探究的，就放手让学生自学；有些知识是需要经历独立思考、相互交流、教师引导才能加深理解的，则要大张旗鼓地进行导学。“自主”则是在教师指导、帮助下的自主。教学真正体现了“教师是数学学习的组织者、引导者与合作者”这一新课程理念，学生不仅学有所得，而且学有所悟。

知识获取后的有效提升

很多数学问题的解决，如果一下子交给学生自主探索，就会出现盲目性的探索活动，如何在引导学生探索之后提升学生的能力，就需要教师在活动之后要给予及时的方法上的总结，以获得有效的活动经验。例如人教版二年级下册解决问题中的《剪手拉手的四个小人》一课。在教学中，教师通过三次动手操作之后，在第四次的动手操作中，是这样帮助学生获得活动经验，提升学生学习能力的：

师：现在我们来理一理思路，你们觉得怎样能保证成功地剪出4个手拉手的小人？

生：要对折三次；小人的图案要画在纸张的封口那侧；小人的手要画到纸张边缘。

师：你们思路很清晰，好，现在开始动手吧！（学生进行操作，多数学生成功剪出作品，惊喜、兴奋的心情溢于言表）

师：祝贺大家都成功剪出4个小人，仔细观察这4个小人，你还有什么发现？

生：是通过把1个小人平移得到4个小人的。

师：你们真厉害，平移的4个手拉手小人我们会剪了，想挑战一下下面的图吗？（出示旋转的手拉手的4个小人图）

（学生进行拓展尝试）

【评析】有了前面的三次动手操作，经过几次的解决问题策略的调整，学生在头脑里已能清晰地对如何剪出手拉手的四个小人有明确的理解，这时教师及时总结提炼，就会更加突出了对几个关键点的认知——对折三次；图案要画在对称轴一侧，且要画至纸张边缘处。学生通过回顾，对此了然于心，空间观念搭建成功，不仅在课堂上获得了成功体验，而且还达成了情感态度方面的教学目的。

有效的课堂教学离不开教师在教学过程中的关键环节的问、讲、点，只有像这样的适时引导、合理调控、及时总结，才会让我们的课堂真正得高效起来。

(作者单位：山西省晋中市寿阳县教研室）