基于导频的OFDM系统信道估计算法的研究

刘国英，李建平，丁鲜花

（国家无线电监测中心陕西监测站，西安 710200）

基于导频的OFDM系统信道估计算法的研究

刘国英，李建平，丁鲜花

（国家无线电监测中心陕西监测站，西安 710200）

本文针对正交频分复用（OFDM）系统中导频信道估计算法，研究了几种常用的导频信道估计算法和插值算法，通过理论分析和实验仿真，分别对比分析了几种导频信道估计算法和插值算法的性能，为工程应用提供理论和实验依据。

正交频分复用；导频；信道估计；插值算法

1 引言

OFDM技术在4G LTE技术中已得到使用，是LTE三大关键技术之一，预计在5G也会延续使用[1]。信道估计技术是无线通信中的关键技术之一[2-3]，最大似然检测、分集接收、自适应的信道均衡估计器等先进的接收技术都需要用到信道估计，信道估计技术是OFDM的关键技术之一。常用的信道估计方法主要有三类，第一类是基于导频辅助调制的信道估计方法[4]，第二类是基于判决指导的信道估计方

法[5-6]，第三类是盲信道估计方法[7]。本文主要研究分析了第一类。

2 OFDM系统中基于导频的信道估计原理

2.1 OFDM系统的组成

OFDM系统的基本框图如图1所示，本文所进行的导频信道估计仿真是在此系统模型下完成的。

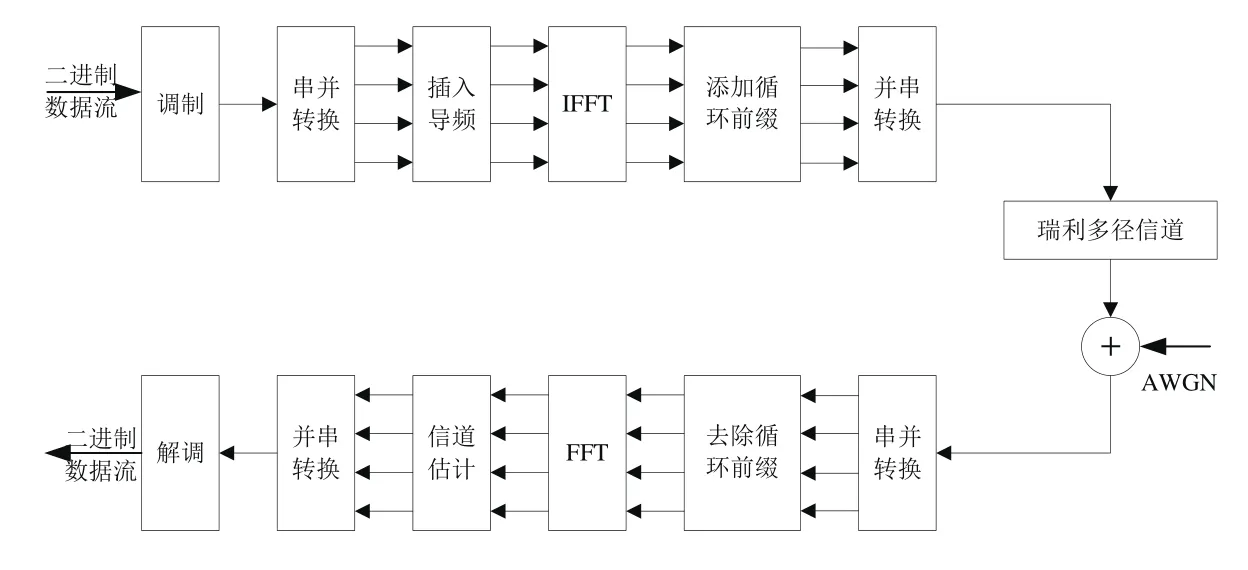
图1 OFDM系统基本模型

2.2 基于导频的信道估计原理

信道估计就是估计从发射端到接收端之间的无线通信链路的时域或频域冲激响应，对于OFDM系统来说，就是估计每个符号或每个子载波的时域响应或频域响应。基于导频的信道估计原理是在发送端的适当位置插入导频符号，在接收端通过接收到的导频符号来估计导频信道的信息，然后再利用插值算法来获取整个数据信道的信息。

3 导频位置处的信道估计算法

在不考虑符号间干扰和子载波间干扰的情况下，OFDM系统模型可以表示为

Yp=XPH+WP（1）

式中，XP为发送的已知导频信号；Yp为接收端接收到的导频信号；WP为导频子信道上叠加的高斯白噪声；H为导频信道处的频率响应值。所谓导频位置的信道估计就是对导频位置处的信道频率响应H进行估计。

3.1 基于LS的信道估计

最小平方信道估计（LS）是从最小平方的意义上得到的信道估计算法。LS准则就是对导频信道响应H进行估计，假设代价函数表达为

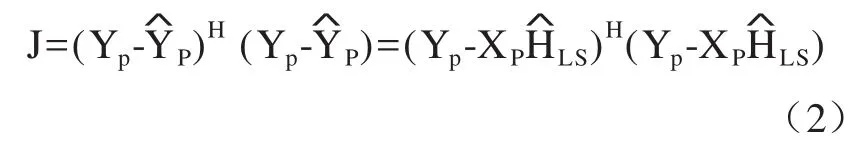
式中，Yp和XP的含义前文有描述；是经过信道估计后得到的导频符号的输出；是导频信道响应H的估计值；LS估计就是要求得在使得上述的代价函数式取得最小值时的取值。

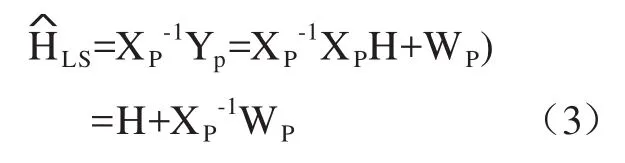
式中，WP是高斯白噪声。

3.2 基于MMSE的信道估计

3.2.1 MMSE算法最小均方误差信道估计（MMSE）

算法采用均方误差（MSE）作为信道估计准则，即使得实际导频信道响应和估计出的导频信道响应差的均方误差值最小。假设代价函数式为

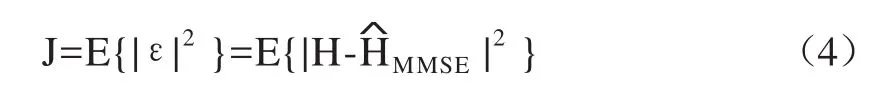
式中，RHY是导频位置信道传输函数与所接受信号的互协方差矩阵；RYY是导频位置处接收信号的自协方差矩阵

式中，RHH是信道传输函数的自协方差矩阵；σn

2是高斯白噪声的方差。

MMSE算法在进行最优化求解时考虑了信道模型和加性噪声的影响，然而MMSE算法需要对矩阵进行求逆运算，当OFDM系统的子载波数目增大时，矩阵的运算量也就变得十分巨大。

3.2.2 LMMSE算法

为了降低MMSE算法的复杂度，出现了一种低阶的基于频域相关的信道估计算法，即LMMSE算法。在计算MMSE时会用到信道的自相关矩阵RHH，是用来表征信道的功率时延谱的，一般不会随着OFDM符号的变化而改变，因而可以看成一个常量，而(XPXP

H)-1则随着OFDM符号的变化而变化，导致计算量增大，假设OFDM符号都采用相同的调制方式，可以用(XPXPH)-1的期望来代替(XPXP

H)-1，并且

式中，I代表单位矩阵。

综上，可得LMMSE估计算法为

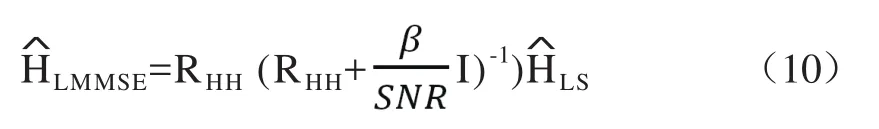
式中，β=E{Xk2}E{|1/Xk|2}，是与调制方式有关的常数；SNR=E{|1/Xk|}/σn2是信噪比。

3.2.3 SVD算法

LMMSE算法的复杂度相比MMSE算法降低了很多，但是当信道发生改变时，（10）式需要重新计算。为了进一步减小复杂度，有学者提出一种更为有效的估计算法，即奇异值分解（SVD）算法。对信道的自相关矩阵进行奇异值分解，得

式中，U是包含奇异向量的归一化矩阵；∧是对角矩阵；对角线上的元素为RHH的特征值，且λ1≥λ2≥…λN。将RHH=U∧UH代入（10）式中得到SVD信道估计为

式中，Δ是一个对角矩阵，对角线上的元素为

式中，λk可以认为是LS经过变换后得到的数据中所包含的信道能量，因而可从N个点中选取P个最大的点，认为这P个点中所包含的信道能量大于噪声，保存下来，而其余的N-P个点信道能量小于噪声，对其进行置零，通常情况下，P取循环前缀的长度，这样矩阵就可以进一步的进行降阶，算法复杂度也会得到进一步的降低，降阶后，对角线上的元素为

这样，就实现了SVD的降阶处理，估计器每一个导频信号只需要2P次乘法运算，既可以降低矩阵阶数，又可以减小噪声的影响。

4 数据位置处的插值算法

基于导频的OFDM信道估计系统中，为了得到完整的信道响应，在通过一定的准则得到导频位置的频率响应估计值后，可以通过插值的方法来估计数据点处的信道信息。采用不同的插值算法，性能是不同的，对系统的影响也很大，常用的插值算法有常值插值、线性插值、高斯插值和FFT插值。

4.1 线性插值

线性插值是一种简单的插值算法，它利用前后相邻的两个导频信道响应的估计值进行线性内插，对于第k个子信道，mL≤k≤(m+1)L，应用线性插值得出信道的频率响应为

式中，L是导频间隔；l是数据子载波相对于前一个相邻导频的偏移量；P(m)是导频位置的频率响应；(k)是相邻两导频间的数据位置处的频率响应。

4.2 高斯插值

高斯插值也称为二阶线性插值，是利用相邻的前后三个导频子信道信息进行二阶插值的方法。对于第k个子信道，高斯插值的算法为

式中，各个系数的定义为

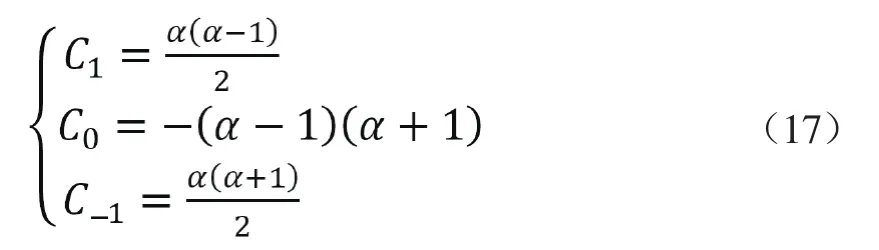
式中，α=m/L；m是数据子载波相对于前一个相邻导频的偏移量，0≤m≤L；L是导频间隔；k是介于第P个导频和第P+1个导频之间的数据位置，PL≤k≤(P+1)L；P是导频的相对位置，P=1,2,…NP-1；NP是导频的个数。

4.3 三次样条插值

三次样条插值属于三次曲线插值，在插值过程中使用了更多的点，估计准确度更高，对于第k个子信道，三次样条插值算法为式中，P'(m+1)是P(m+1)的一阶导数；。

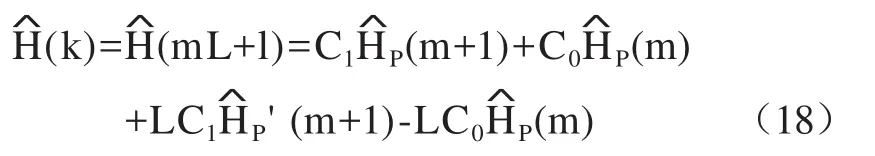
4.4 FFT插值

FFT插值算法利用了信号处理过程中在时域补零等效于在频域进行插值的原理来恢复出信道的频率响应。它的基本思想是：将导频位置处的频率信道响应估计值经过IFFT变换到时域，然后在时域进行补零处理，再通过FFT变换回频域，从而得到所有数据位置处的信道响应估计值。其基本框图如图2所示。

图2 FFT时域插值方法框图

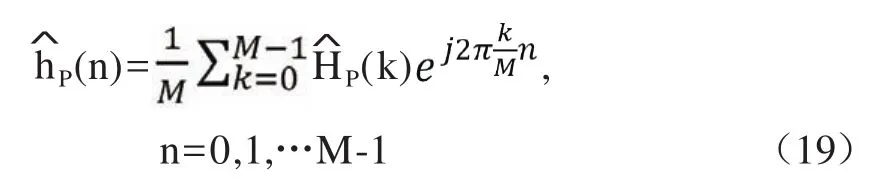
然后，在时域信号中间或者尾部进行补零，就得到了N点的时域序列N(n)，再对N(n)进行N点FFT式中，N(k)为所有位置的频率响应估计值。

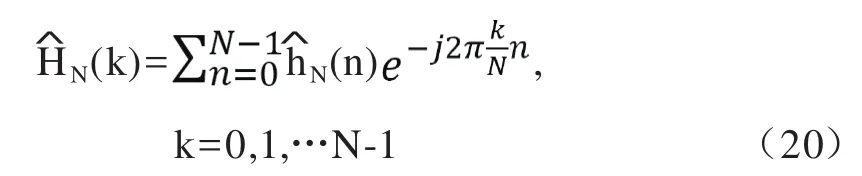
5 仿真分析

5.1 不同导频位置处信道估计算法的仿真与分析

采用块状导频结构，系统带宽为5MHz，载波频率为2GHz，子载波数为128，循环前缀为32。信道模型为带多普勒频移的瑞利多径衰落信道和高斯白噪声的组合信道，最大多普勒频移为50Hz，多径个数为6，最大多径时延为3.5μs，多径信道的幅度相互独立，其满足负指数分布的功率延迟谱p(τ)=exp(-τ)/τrms)，τ为各径的时延，τrms一般取循环前缀长度的1/4。

图4和图5给出了LS算法和MMSE算法以及两种简化的MMSE算法（LMMSE算法和SVD算法）的BER和MSE曲线图。

图3 LS，MMSE，LMMSE，SVD信道估计和无信道估计的误码率比较

图4 LS，MMSE，LMMSE，SVD信道估计算法的均方误差比较

通过图3可以看出信道估计的必要性，在无信道估计的情况下，系统的误比特率较大。在有信道估计的情况下，图3和图4可以看出，LS算法的估计效果最差，MMSE算法考虑了噪声的影响，估计的精度提高，性能最好，当然其算法的复杂度也是最高的。LMMSE算法性能较MMSE算法的性能有一定的损失，SVD算法在性能上和LMMSE相差不多，但算法的复杂度却大大降低。

通过以上仿真结果和分析可以看出，LS准则算法复杂度低，实现简单，适用于信道条件较好时。MMSE准则算法复杂度较大，实现复杂，可以使用它的简化算法，其中，SVD算法较LMMSE算法复杂度降低很多，而性能并没有太大的损失，性价比更高，因而，当信道条件恶劣时，采用SVD准则就可以达到较理想的信道估计性能。

5.2 不同插值算法的仿真与分析

OFDM系统仿真参数：梳妆导频结构，系统带宽为5MHz，载波频率为2GHz，子载波总数为128，循环前缀为16，16QAM调制方式。信道为瑞利多径衰落信道和高斯白噪声的组合信道，多径个数为6，最大多径时延为5μs，最大多普勒频移为100Hz，多径信道的幅度相互独立，其满足负指数分布的功率延迟谱p(τ)=exp(-τ/τrms)。

图5和图6分别是在LS估计导频位置的信道频率响应后，分别进行线性插值，高斯插值，三次样条插值和FFT插值的BER和MSE曲线图。

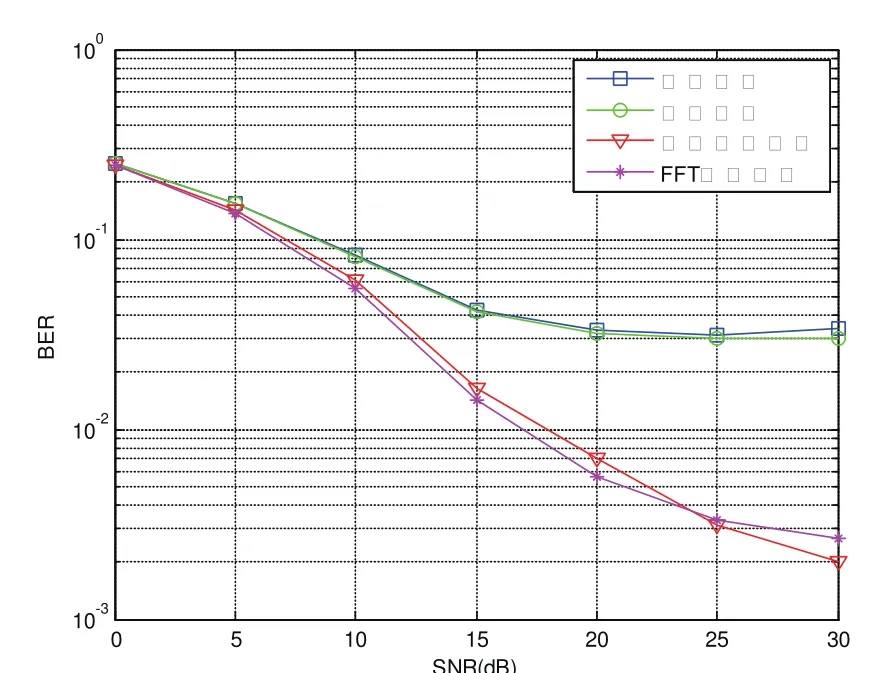
图5 不同插值算法的误码率比较

图6 不同插值算法的均方误差比较

从图5和图6可以看出，线性插值和高斯插值在低信噪比的时候性能和其他算法差别不大，但是在高信噪比的时候会出现地板效应。三次样条插值算法的性能随着信噪比的增大而得到提高，低信噪比的时候性能较差，高信噪比性能显著提高。FFT插值算法无论在低信噪比还是高信噪比的情况下都表现出了较好的性能。

实际在选用插值算法的时候，可以根据具体的信道条件以及实际的需求进行选择，由前文分析可知，线性插值和高斯插值算法复杂度相对较低，在低信噪比时可以选用比较简单的线性插值算法，并且性能良好。对于三次样条插值算法，算法本身的复杂度较高，在低信噪比时的性能较差，其对信道估计性能的影响远大于插值算法本身所能提供的性能改善，因而适合在高信噪比的情况下使用。而FFT时域插值方法无论是在低信噪比还是高信噪比的情况下性能都较好，且复杂度较低，实时性较高，是一种比较折中的估计方法。

6 结束语

本文针对OFDM系统，理论分析和实验仿真了几种不同导频位置的信道估计算法和数据位置的插值算法，每一种算法都有其各自的性能特点，可根据实际需求进行应用。■

[1] 田忠驿．5G关键技术浅谈[J]．移动通信，2015,39(13):92-96

[2] 佟学俭，罗涛．OFDM移动通信技术原理与应用[M]．北京：人民邮电出版社，2003

[3] 罗仁泽．新一代无线移动通信系统关键技术[M]．北京：北京邮电大学出版社，2007

[4] 张继东，郑宝玉．基于导频的OFDM信道估计及其研究进展[J]．通信学报，2003,15(2):25-31

[5] O. Edfom, M. Sandell, JJ. Van de Beek, et al. OFDM channel estimation by singular value decomposition [J], IEEE Transactions on Communications, 1998, 46(7): 931-939.

[6] Ahamad Chini, Yiyan Wu ,et. al. Filtered Decision Feedback Channel Estimation for OFDM Based DTV Terrestrial Broadcasting System [J], IEEE Transactions On Broadcasting, 1998, 44(1):2-11.

[7] R. W. Heath Jr, G. B. Giannakis, Exploiting input cyclostationarity for blind channel identification in OFDM system [J], IEEE Transactions on Signal Processing, 1999, 47(3):848-856.

VMware推出全新云管理平台解决方案

VMware近期宣布正式推出VMware vRealize Automation 7与VMware vRealize Business Standard 7，进一步助力IT部门推动其所在企业的数字业务转型。

Study of Channel Estimation Algorithm Based on Pilot in OFDM System

Liu Guoying, Li Jianping, Ding Xianhua (Shanxi Radio Monitoring Station, The State Radio Monitoring Center., Xi'an, 710200)

This paper is aimed at channel estimation algorithm based on pilot in orthogonal frequency division multiplexing (OFDM) system. Several frequently used channel estimation algorithms based on pilot and interpolation algorithms are studied. The performance comparisons of different channel estimation algorithms are made through theoretical analysis and computer simulation as well as interpolation algorithm. It provides evidence for theory and experiment in engineering applications.

OFDM; pilot; channel estimation; interpolation algorithm

10.3969/J.ISSN.1672-7274.2016.01.015

TN919.3 文献标示码：A

1672-7274（2016）01-0063-05

刘国英，硕士研究生，助理工程师，现任职于国家无线电监测中心陕西监测站。