明渠梯形断面消力池池深和尾坎高度的计算方法

张志昌，赵 莹,2，王学斌

(1.西安理工大学 水利水电学院，西安 710048; 2.中国电建集团西北勘测设计研究院有限公司工程实验检测分院，西安 710000; 3.中国水电建设集团 第十五工程局有限公司，西安 710065)



明渠梯形断面消力池池深和尾坎高度的计算方法

张志昌1，赵 莹1,2，王学斌3

(1.西安理工大学 水利水电学院，西安 710048; 2.中国电建集团西北勘测设计研究院有限公司工程实验检测分院，西安 710000; 3.中国水电建设集团 第十五工程局有限公司，西安 710065)

为研究明渠梯形断面消力池池深和尾坎高度的计算方法，依据前人对梯形断面消力池水跃共轭水深、梯形断面量水堰(槛)的研究成果，采用能量方程研究梯形断面挖深式消力池、消力坎式消力池和综合式消力池深度和坎高的计算方法。给出了梯形断面消力池池深、尾坎高度的计算公式，通过算例说明了计算过程。提出的消力池深度、坎高的计算公式可以作为梯形断面消力池设计的参考。

明渠；梯形断面；消力池；池深；尾坎高度；水力计算

1 问题的提出

明渠梯形断面是明渠最常用的断面形式之一。梯形断面消力池的设计主要为水跃共轭水深、水跃长度和消力池深度或尾坎高度的计算。梯形断面形状比较复杂，水跃共轭水深的计算需求解一元四次或一元五次方程，计算比较繁琐。近年来许多学者对水跃共轭水深的计算做了研究，文献[1-2]通过求解一元四次方程，给出了水跃共轭水深显式精确解；文献[3]根据水跃函数曲线的性质和几何意义，提出了梯形明渠水跃共轭水深的简化计算公式；文献[4]通过引入单位水面宽度的概念，提出了梯形明渠水跃共轭水深的直接计算公式；文献[5]从梯形明渠水跃共轭水深方程出发，给出了最简单的水跃共轭水深的迭代公式。

对矩形断面消力池深度、尾坎高度的计算已有比较成熟的研究成果[6-8]，但对于梯形断面消力池的池深和尾坎高度的计算成果甚少。梯形断面消力池的跃后水深较小，消能率较高。文献[9]比较了矩形、梯形和三角形断面水跃的消能率，认为梯形断面消力池的消能率大于矩形断面；文献[10]通过模型试验，研究了梯形断面消力池跃后水深与下游尾水深的关系，认为梯形断面消力池可显著降低池内的水深，因此可以降低工程造价，但没有给出消力池尾坎高度的计算方法；文献[11]认为，应该利用梯形断面明渠中水跃共轭水深小的优点，对梯形断面水跃消力池做进一步的研究；文献[12]认为，在设计消力池时，应优先考虑矩形断面，若需采用扩散式或梯形断面消力池，应保证池内不发生侧向回流，对消力池深度或尾坎高度需经水工模型试验确定；文献[13]认为，在设计挖深式消力池时，梯形断面消力池深度的计算方法与矩形断面消力池深度的计算方法相同，对于消力坎高度和综合式消力池，没有给出计算方法；文献[14]对梯形断面消力池进行过模型试验，认为在梯形断面消力池的适当位置设置实体坎，梯形消力池比矩形消力池有更大的安全系数，但实体坎的位置、高度需通过水工模型试验确定。

由以上研究可以看出，目前对梯形断面消力池的研究主要集中在消力池水跃的共轭水深方面，对消力池池深、消力坎的高度研究甚少。梯形断面是明渠最重要的断面形式之一，消力池深度和尾坎高度的研究对工程设计具有重要意义，所以本文在总结前人对梯形断面明渠水跃共轭水深、梯形断面量水堰(槛)研究的基础上，根据能量方程寻求梯形断面消力池深度和尾坎高度的计算方法，为工程设计提供基础研究。

2 梯形断面水跃的共轭水深和水跃长度的计算

对于已知跃前水深求跃后水深的情况，梯形断面的水跃方程[15]为

(1)

其中：

式中:m为梯形断面的边坡系数；h1和h2分别为跃前和跃后断面水深；b为梯形断面的底部宽度；Q为流量；g为重力加速度。

(2)

(3)

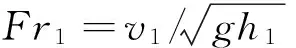
(4)

式(4)为一元四次方程，可以根据一元四次方程的解法，文献[1-2]给出了精确解，但计算过程较繁锁。文献[5]给出了梯形断面水跃共轭水深最简单的迭代公式为

(5)

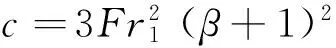
对于已知跃后水深求跃前水深的情况，水跃方程可以写成下列形式：

(6)

其中：

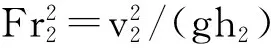
式中v2为跃后断面流速。

文献[5]给出式(6)的迭代式为

(7)

梯形断面的水跃长度可以按照刘韩生等[16]的公式计算，即

(8)

式中B1和B2分别为跃前和跃后断面的水面宽度。

3 梯形断面消力池池深和尾坎高度的计算

3.1 梯形断面挖深式消力池深度的计算

梯形断面挖深式消力池深度的计算方法与矩形断面消力池相同，但梯形断面计算过程比矩形断面更复杂，需用试算法。梯形断面挖深式消力池如图1所示。

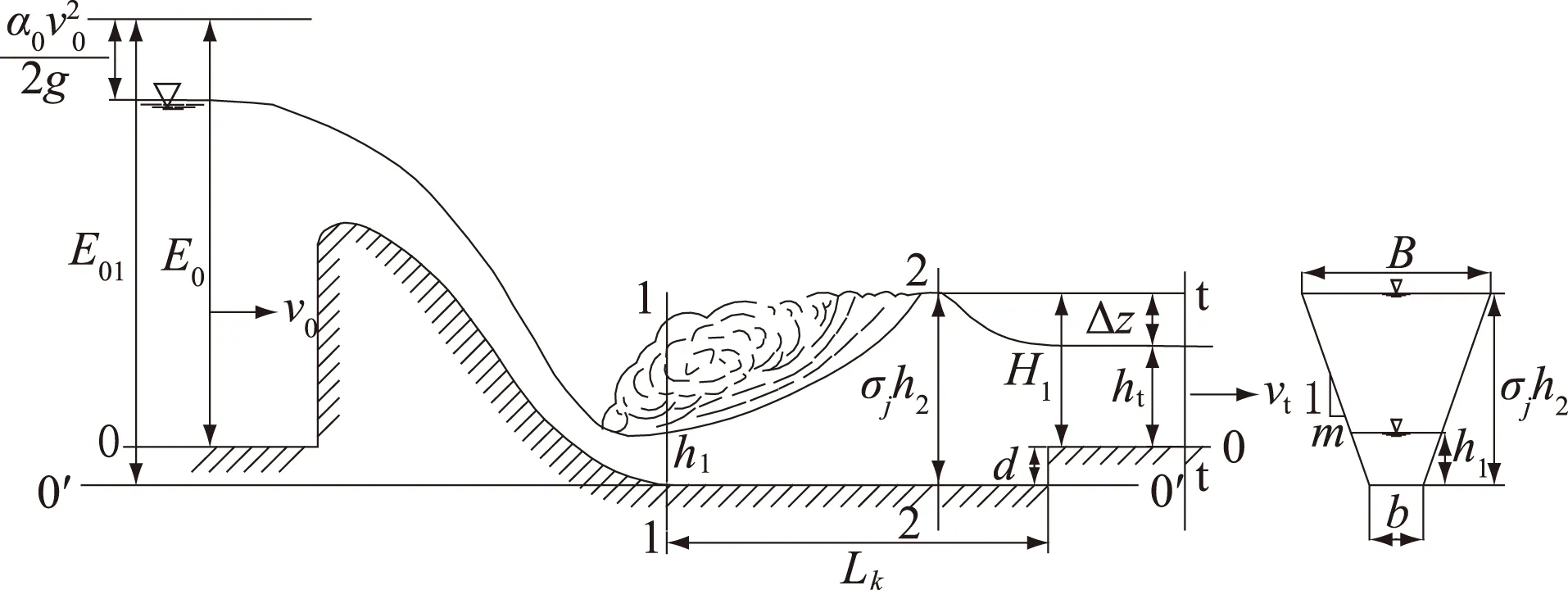
图1 梯形断面挖深式消力池深度计算简图Fig.1 Caculation diagram of deepened stilling basin depth of trapezoidal cross section

消力池深度的计算方法如下：已知梯形断面的底宽为b，边坡系数为m，消力池原河床以上总水头为E0，流量为Q，溢流面的流速系数为φ。设消力池的深度为d，跃前水深为h1，跃后水深为h2，下游水深为ht，消力池出口下游水面降落为△z，由图1的关系中可以看出：

(9)

式中：σj为水跃的淹没系数，一般取σj为1.05～1.1，常采用1.05。以图1中的0′-0′为基准面，写上游断面和消力池1-1断面的能量方程得

(10)

式中：A1为跃前断面的面积；如果已知跃前水深，跃后水深用式(5)计算。以下游河床0-0为基准面，写2-2断面和t-t断面的能量方程得水面降落为

(11)

式中：ht为下游河床水深；φ′为消力池出口的流速系数，一般取0.95；A2为跃后断面的面积；At为下游水深断面处的面积。跃前断面和跃后断面均为梯形断面，断面面积为

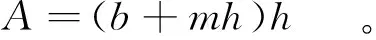
(12)

计算跃前断面面积时，水深用h1，计算跃后断面的面积时，水深用h2。

由以上梯形断面消力池深度的计算方法可以看出，该方法与矩形消力池深度的计算方法完全相同，文献[13]在计算梯形断面消力池深度时，亦采用与本文相同的方法，所不同的是在计算消力池后的水面降落Δz时忽略了跃后断面的行进流速水头，即式(11)中右边的第二项，并建议消力池出口的流速系数φ′=1.0，而我国则多采用φ′=0.95。

算例1：有一底宽b=5 m，边坡系数m=1，通过的流量Q=33.6 m3/s，具有底坡i=0.057的大于临界底坡的梯形渠道与一小于临界底坡的渠道连接。已知第一段渠道末端水深h1=0.5 m，第二渠道水深ht=2.0 m，流速vt=1.2 m/s，溢流面的流速系数φ=0.95，消力池后的流速系数φ′=0.95，试设计一挖深式消力池。

(1) 判断是否需要修建消力池：

A1=(b+mh1)h1=

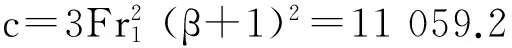
迭代得η=6.532 87，跃后水深h2=ηh1=6.532 87×0.5=3.266 4 m，h2>ht=2.0 m，需要修建消力池。

(2) 计算下游河床以上总水头：

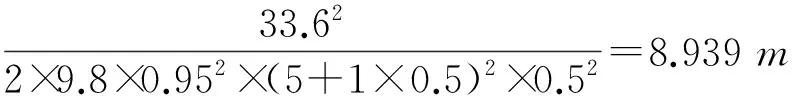
(3) 消力池深度计算过程：

设消力池的深度为di=1.0 m，E01=E0+di=8.939+1.0=9.939 m。因为

由上式得h01的迭代式为

由上式迭代得h01=0.474 354 m。

(5+1×0.474 354)×0.474 354=2.596 78m2；

33.62/(9.8×0.474 354×2.596 782)=36.014 68 ；

a1=(2.5β+1)=27.351 63，

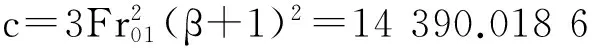
代入式(5)迭代得η=7.082 62，跃后水深为

h02=ηh01=7.082 62×0.474 354=3.359 67m；

取消力池的淹没系数σj=1.05，则有

3.359 67)×1.05×3.359 67=30.082 6m2；

v02=Q/A02=33.6/30.082 6=1.116 925m/s；

1.05×3.359 67-2-0.017 76=1.51m。

与假设不符，重新假设消力池深度di，重复上面的计算过程，列表计算见表1。

由表中可以看出，当di=1.557 955 m时，计算值与假定值相同。实际工程可取消力池深度为1.56 m。

跃前和跃后断面的水面宽度分别为：

B2=b+2mσjh2=

5+2×1×1.05×3.407 8=12.156 4m。

由B1和B2可求得消力池的长度为：

5×1.05×3.407 8×{1+[(12.156 4-

5.923 5)/5.923 5]0.25}=36.011m;

Lk=0.8Lj=0.8×36.011=28.809m。

3.2 梯形断面消力池尾坎高度的计算

梯形断面消力池尾坎高度的计算简图见图2，可以仿照矩形断面消力坎的计算方法来计算梯形断面消力坎的高度。由图2可以看出，消力坎的高度为

(13)

(14)

式中：c为坎高；H1为消力坎顶以上的水深；H10为消力坎顶以上总水头。

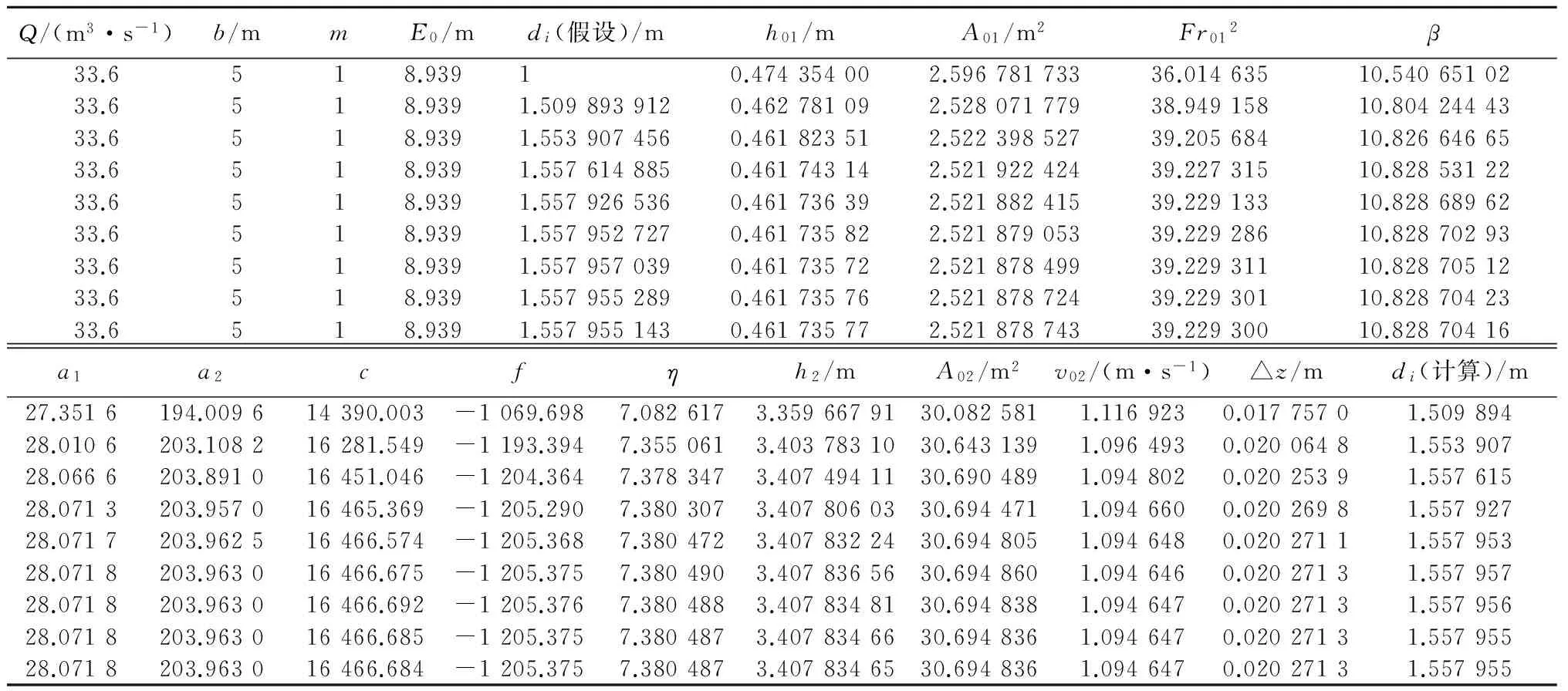
表1 算例1计算结果

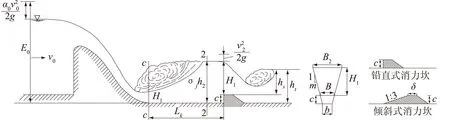
图2 梯形断面消力坎式消力池Fig.2 Stilling basin of trapezoidal cross section with baffle wall style

梯形断面消力坎相当于1个矩形与1个三角形断面组合的梯形堰，文献[17]已给出了流量计算公式为

(15)

式中：m0为流量系数；B为消力坎顶部垂直于水流方向的宽度。将式(14)变形代入式(15)得

(16)

文献[18]介绍了梯形渠道上应用的量水槛，所谓量水槛，实际上就是将平顶堰的上游铅直面改成倾斜面，其倾斜坡比为1∶3，下游面可做成斜面，也可做成铅直面，如图2所示。文献[18]未给出流量计算公式，在渠道设计中采用查表的方法计算流量。目前正在审查的我国灌溉渠道系统量水规范给出了梯形渠道量水槛流量的计算公式为：

(17)

(18)

式中：hk为量水槛上的临界水深；Cd为流量系数；δ为堰顶厚度。式(18)的适应条件为0.1≤H10/δ≤1.0。

梯形断面的临界水深可用下面的迭代公式计算[15]，即

(19)

下面分析流量系数的取值问题。如果将消力坎上游做成1∶3的斜坡式坎，可以应用式(17)计算梯形消力坎通过的流量，用式(18)计算流量系数。消力坎一般为梯形实用堰，其堰顶宽度δ与堰上水头H10的比值应在0.67～2.5之间，根据式(18)的适应条件，如果要把量水槛应用到梯形渠道消力坎的设计中，则1≤δ/H10≤2.5，即0.4≤H10/δ≤1.0，代入式(18)求得流量系数Cd在0.986 45～0.999 33之间，在计算时可以近似取0.99。

如果将消力坎的上游做成铅直面，流量系数m0的取值比较复杂，目前尚未看到这方面的研究成果。文献[17]研究过设在渠道中的缝式堰，所谓缝式堰是指设在渠道中断面为梯形的墩座，当水流通过墩座时，在墩座后产生水面降落，其流量计算公式与式(16)一样，但研究者的流量系数差异较大，根据E. A.窿马林院士的意见[17]，在墩座外形匀缓的条件下，当H1<1.0 m,H1=1.0～1.5 m,H1=1.5～2.0 m和H1=2.0～2.5 m时，流量系数m0分别为0.475，0.485，0.495和0.510；文献[9]认为，对于宽顶堰流量系数m0=0.35～0.37，对于实用堰，m0=0.44～0.50。文献[18]认为，当H1/B=0.5，1.0，1.5，2.0，2.5时，流量系数m0为0.37，0.415，0.43，0.435，0.45，显然，流量系数m0为0.37是宽顶堰的流量系数。缝式堰的流量系数没有体现梯形墩厚度与渠宽的比值对流量系数的影响，且流量系数的选择任意性较大，在实际应用中存在较大的难度。文献[19]认为，在计算消力坎高度时，梯形断面消力坎以上水面宽度应取其平均宽度B+0.8mH1，这对于纵断面为矩形和梯形的消力坎，流量系数m0=0.42。由于目前尚未看到更好的计算梯形渠道流量的量水设施，所以在采用式(16)计算梯形渠道消力池消力坎通过的流量时，仍近似取流量系数m0=0.42。

下面以式(16)计算流量为例，说明计算消力坎高度的步骤：

(1) 假定一个坎高c，求得B=b+2mc，代入式(16)求H1，将式(16)写成迭代形式为

(20)

(2) 将求得的H1代入式(13)求坎高c，如果求得的坎高c与假设相同，坎高即为所求，否则需另假设坎高c，重复上述步骤，直到达到所需的精度为止。

算例2 ：同例题1，试设计一消力坎式消力池。

由算例1已求得跃后水深h2=3.266 4 m，已知边坡系数m=1，取m0=0.42。

设消力坎高度为c=2.0 m，由式(20)得

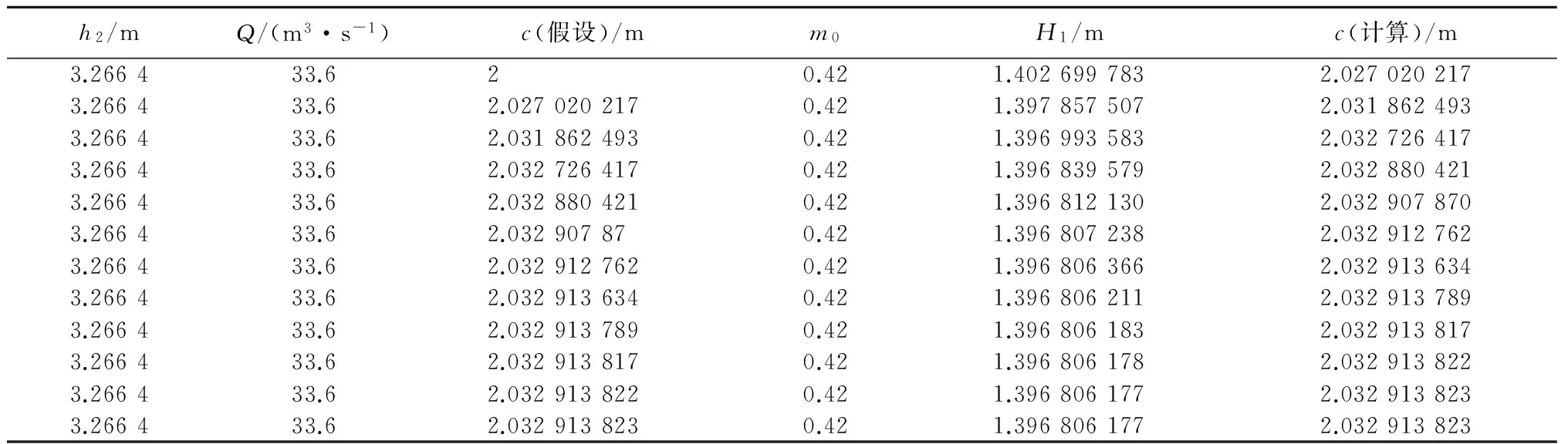
表2 算例2消力坎高度计算结果

由上式迭代得H1=1.402 7 m，则

1.05×3.266 4-1.402 7=2.027 02m。

与假设不符，重新假设c，列表计算见表2。

由表2可以看出，消力坎高度可取c=2.033 m。

如果用式(17)求流量，则计算步骤为：

(1) 假定一个坎高c，求B=b+2mc，根据已知流量用式(19)求临界水深。

(2) 取流量系数Cd=0.99，代入式(17)求H10。

(3) 将H10代入式(14)求H1。

(4) 将H1代入式(13)求坎高c，如果求得的坎高c与假设的相同，坎高即为所求，否则需另假设坎高c，重复上面的步骤，直到达到所需的精度为止。

仍以该算例为研究对象，设消力坎为斜坡式，经试算求得hk=1.093 m，H10=1.595 m，H1=1.526 m，坎高为c=1.904 m。2种算法相差6.3%，一般消力坎上游多为铅直式，在初步设计时可以近似的取m0=0.42。

3.3 梯形断面综合式消力池的计算

综合式消力池见图3，由于梯形断面消力池后水流的衔接形式比较复杂，可能从梯形断面过渡为矩形断面，也可能仍然为梯形断面，如果采用矩形断面综合式消力池的计算方法，计算过程十分复杂。现根据梯形断面综合式消力池的几何关系，计算综合式消力池的坎高和深度，计算过程相对简单一些。

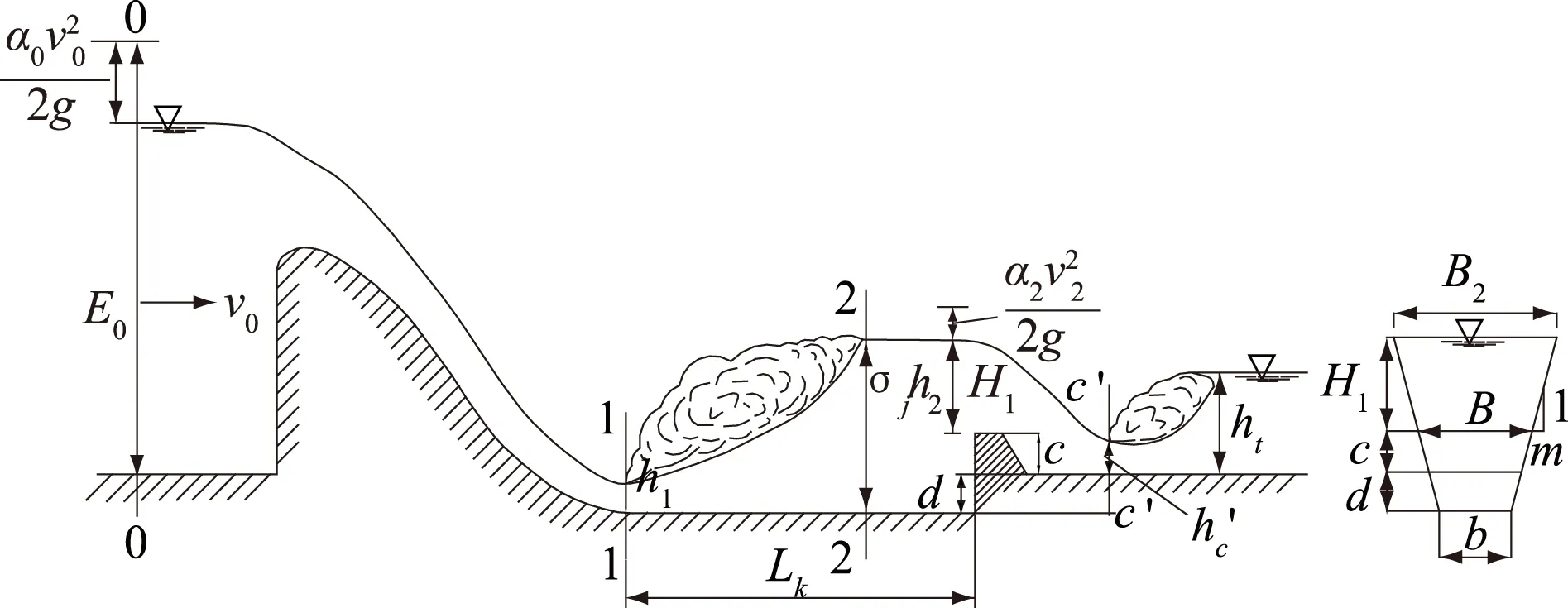
图3 梯形断面综合式消力池Fig.3 Stilling basin of trapezoidal cross section with comprehensive style

由图3可以看出：

(21)

消力坎顶部的宽度B为

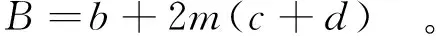
(22)

将式(22)代入式(16)得

(23)

计算时，先假定一个消力池深度d，用式(10)计算跃前断面水深h1，式(10)的迭代式为

有了h1，可以计算β=b/(mh1)，有了β，可以计算a1，a2，c，d，将计算结果代入式(5)求梯形断面的共轭水深比η，从而根据h2=ηh1可求得跃后断面的水深h2。取σj=1.05，代入式(21)变形得

(24)

将式(24)代入式(23)得

(25)

从式(25)中解出H1，得H1的迭代式为：

(26)

(27)

计算时，先假设一个消力池深度d，由式(23)求跃前断面水深h1，由式(5)计算水跃的共轭水深η，则跃后水深为h2=ηh1，由式(26)求消力坎上水深H1，由式(27)求坎高c。

算例3 ：同例题1，试设计一综合式消力池。

由算例1已知，E0=8.939 m，取m0=0.42，假设d=1 m，由算例1已求得d=1.0 m时，跃后水深h2=3.359 67 m，将所求得的h2代入式(26)求出H1为1.382 m，再代入式(27)求得坎高c=1.146 m。

当求出坎高c后，还要校核坎后的水流流态，其方法与矩形断面消力池相同，此处不再赘述。

4 结 语

据文献[16]报道，为了节省工程量，陡坡消力池多数具有梯形断面。但梯形断面消力池池深、尾坎高度至今没有理论计算方法，一般需通过模型试验确定。本文在总结梯形断面水跃共轭水深、梯形断面缝式堰和量水槛的研究成果的基础上，研究了梯形断面挖深式消力池深度、消力坎式消力池尾坎高度和综合式消力池池深和尾坎高度的计算方法。但需注意的是，梯形断面消力池的水流流态具有不对称性，消力池内会发生强烈的立轴旋涡，本文只提供了计算梯形断面消力池深度和尾坎高度的一种理论计算方法，作为梯形断面消力池设计的基础。至于消力池内的流态，可以参照文献[14]在消力池中设置消力坎或者“人”字分流坎[20]等措施加以改善。另外梯形断面尾坎的流量系数的研究成果很少，还需要进一步积累和研究。

[1] 王学斌, 张 毅.梯形明渠水跃共轭水深的精确解[J]. 电网与清洁能源, 2013, 29(11):118-122.

[2] 王兴全. 梯形明渠水跃共扼水深的计算[J]. 农田水利与小水电, 1989,(9)：16-18.

[3] 刘计良, 王正中, 杨晓松, 等. 梯形渠道水跃共轭水深理论计算方法初探[J]. 水力发电学报, 2010, 29(5)：216-219.

[4] 赵延风, 王正中, 芦 琴, 等. 梯形明渠水跃共轭水深的直接计算方法[J]. 山东大学学报, 2009, 39(2)：131-136.

[5] 张志昌, 赵 莹. 梯形断面明渠水跃共轭水深新的迭代方法[J]. 西安理工大学学报, 2014, 30(1)：67-72.

[6] 张志昌, 李若冰. 基于动量方程的挖深式消力池深度的计算[J]. 西北农林科技大学学报(自然科学版), 2012, 40(12):214-218.

[7] 张志昌, 李若冰, 赵 莹, 等. 消力坎式消力池淹没系数和坎高的计算[J]. 长江科学院院报, 2013, 30(11)：50-54.

[8] 张志昌, 李若冰, 赵 莹, 等. 综合式消力池深度和坎高的计算[J]. 西安理工大学学报, 2013, 29(1)：81-85.

[9] 吴持恭. 水力学[M]. 北京：高等教育出版社. 2006：283-341.

[10]何塞L. 桑切斯，彭 军，等.溢洪道设计[J]. 水利水电快报, 1998,19(6)：16-18.

[11]倪汉根, 刘亚坤. 击波、水跃、跌水、消能[M].大连：大连理工大学出版社, 2008.

[12]SL253—2000,溢洪道设计规范[M].北京：中国水利水电出版社, 2000.

[13]И. И. АГРОСΚИН.水力学(下册) [M]. 清华大学水力学教研组, 天津大学水利系水力学教研室译. 上海：商务印书馆, 1954：635-644.

[14]吴建平.提高梯形消力池消能效率的试验研究[J]. 郑州工学院学报, 1995,16(3)：28-31.

[15]张志昌.水力学(下册) [M]. 北京：中国水利水电出版社，2011：87-88.

[16]刘韩生, 花立峰, 纪志强, 等. 跌水与陡坡[M]. 北京：中国水利水电出版社，2004：147-151.

[17]Π.Γ基谢列夫.水力计算手册[M]. 陈肇和，译.北京：电力工业出版社, 1957：182-184.

[18]王常德. 量水技术与设施[M]. 北京：中国水利水电出版社, 2006：218-219.

[19]Μ Д切尔陀乌索夫.水力学专门教程[M]. 沈清廉，译.北京：高等教育出版社,1954：322-323.

[20]冯新民. “人”字分流坎在梯形消力池中的运用[J]. 水力发电, 1986,(1)：52-53.

(编辑：曾小汉)Calculation Methods of Stilling Basin Depth and End Sill Height inOpen Channel of Trapezoidal Cross Section

ZHANG Zhi-chang1, ZHAO Ying1,2, WANG Xue -bin3

(1.Institute of Water Resources and Hydroelectric Engineering , Xi’an University of Technology, Xi’an 710048, China; 2.Branch of Engineering Experiment and Inspection，PowerChina Northwest Engineering Corporation Limited， Xi’an 710000, China; 3.Sinohydro Corporation Engineering Bureau 15 Co. ,Ltd., Xi’an 710065,China)

In order to explore the calculation methods of stilling basin depth and end sill height, we summarize previous research results about conjugate depth of hydraulic jump in trapezoidal stilling basin and measuring weir(sill)of trapezoidal cross section. According to energy equation, we present the calculation methods of stilling basin depth and sill height with trapezoidal cross section for 3 types of stilling basin, namely, deepened style, baffle wall style, and comprehensive style. On the basis of this, we put forward calculation formulas of stilling basin depth and sill height and exhibit the calculation process through examples. Finally, the calculation formulas can be taken as a reference for the design of trapezoidal stilling basins.

open channel；trapezoidal cross section; stilling basin；stilling basin depth; end sill height; hydraulic calculation

2014-08-13；

2014-09-20

张志昌(1954-)，男，陕西西安人，教授级高级工程师，主要从事水工水力学方面的研究，(电话)13991942265(电子信箱)zhangzhichang1954@163.com。

10.11988/ckyyb.20140710

2016,33(01):48-53，60

TV135.2

A

1001-5485(2016)01-0048-06