监利站平滩面积对水沙条件变化的滞后响应
廖治棋,范北林,李凌云,王家生,王俊洲
(1.长江科学院 水利部江湖治理与防洪重点实验室,武汉 430010;2.赣州市水利电力勘测设计研究院,江西 赣州 341000)
监利站平滩面积对水沙条件变化的滞后响应
廖治棋1,2,范北林1,李凌云1,王家生1,王俊洲1
(1.长江科学院 水利部江湖治理与防洪重点实验室,武汉 430010;2.赣州市水利电力勘测设计研究院,江西 赣州 341000)
河床对水沙条件变化的滞后调整过程已被众多研究者通过实测资料分析所证实。以荆江河段上的监利站为研究对象,选定平滩面积作为反映河床调整的参数,通过分析河道平滩面积调整的滞后响应过程与特点,探讨其响应调整规律,并建立与之相适应的滞后响应模型。研究表明,监利站的前期来水来沙条件对当前平滩面积调整的影响真实存在,滞后响应理论同样适用于长江荆江河段的监利站。同时,通过对适用于黄河流域的滞后响应模型(即黄河滞后响应模型)进行改进,建立了适用于监利站的平滩面积滞后响应模型。
水沙条件变化;冲积性河流;监利站;平滩面积;滞后响应;河床演变
1 研究背景
河床演变是由水流与河床相互作用中的输沙不平衡所引起的,在水流与河床这对矛盾的2个方面中,来水来沙条件起着决定性作用[1]。根据Leopold等[2]的观点,可以将冲积河流看作是一个具有物质和能量输入和输出的开放系统,认为来水来沙是流域施加于河道的外部控制变量,河床的冲淤变化和河槽几何形态的调整则是内部变量对外部控制条件的响应,结果会使河槽形态朝着与来水来沙相适应的平衡状态发展。这一概念既反映了河流特性取决于流域因素的观点,又强调了系统的自动调整作用[3]。由于河床的冲淤需要一个时间过程,河床演变一般滞后于来水来沙条件的变化,滞后响应是河床调整过程中的一种普遍现象[4-6]。
多年来,水利科技工作者对河道横断面形态调整开展了大量的研究工作[7-12]。但总体看来,以往研究大多侧重于河道的平衡状态。此外,现有的研究成果在计算方法的理论依据和应用范围都还存在着不足,建立能揭示冲积河流河床演变内在机理的理论显得尤为重要。平滩面积作为反映河槽形态特征和河道过流能力的重要指标,能宏观体现河床横断面上的冲淤变化。平滩面积的大小可由平滩水位以下的过水断面面积采用梯形法求得。本文通过引入滞后响应理论,选用平滩面积作为计算参数,分析监利站处河道断面的平滩面积随水沙条件的响应过程与特点,并建立与之相适应的滞后响应模型,对长江中下游冲积性河流的研究以及完善滞后响应理论都有积极的作用。
2 水沙条件变化及平滩面积的响应
2.1 水沙条件变化分析
2.1.1 水流条件变化
根据监利站历年的实测水沙资料分析可知,1981—2002年多年平均流量12 200 m3/s,历年最大平均流量45 700 m3/s,历年最小流量2 450 m3/s(见图1)。监利站不同时期各月平均流量的分析如图2所示,对比2003年三峡建库运营前后监利站流量变化,可以看出建库后监利站年平均流量变小,为11 460 m3/s,比建库前减少6.1%,年内流量分配规律有所变化。建库前汛期流量占总流量的75%,建库后为71.3%,在主汛期6—9月份其平均流量较建库前减少了9.9%,月平均流量建库后较建库前减少了7.1%~12.8%。其中6月份减少了1 107 m3/s,7月份减少了3 234 m3/s,8月份减少了1 826 m3/s,9月份减少了2 091 m3/s。相应地,枯季流量有所增加,一般主汛前(1—4月份)偏大,主汛后(10—12月份)偏小。1—4月的流量平均增幅在5%~25.3%,如2月份平均流量增加了1 086 m3/s,增幅为25.3%。10月份和11月份流量减小幅度分别为24.2%与6.2%,10月份流量减少了3 819 m3/s,减小量较大,12月份基本不变。对比分析建库后监利站流量过程,可以看出1—5月份、11—12月份监利站流量比入库流量增大,6—10月份流量减小,说明三峡水库的运用起到了加大枯水流量、拦蓄洪水的作用。
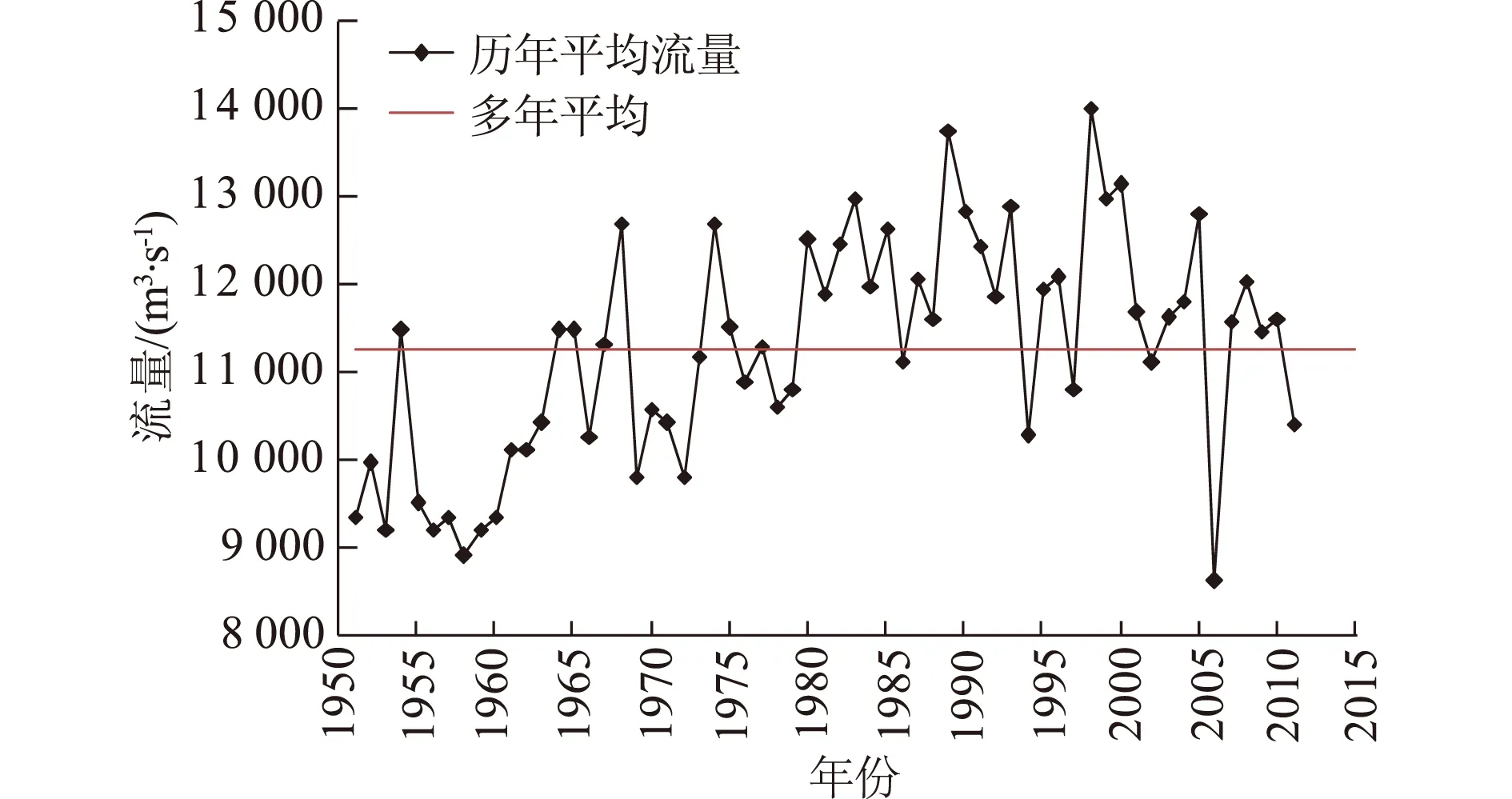
图1 监利站年平均流量变化Fig.1 Variation of mean annual discharge in Jianli station

图2 监利站不同时期各月平均流量对比Fig.2 Comparison of mean monthly discharge at different periods in Jianli station
2.1.2 来沙条件变化
三峡蓄水运用后,坝下游水沙关系发生明显变化。主要表现为同流量下来沙量减小。根据三峡水库蓄水运用以来下游河道观测资料分析,三峡水库运用初期,上游来沙60%被拦蓄在库内[13]。上游来沙中的大量推移质以及悬移质中较粗的部分拦在库内,排往库外的则主要是悬移质中较细的部分,同流量下出库含沙量显著减小,下泄水流挟沙处于次饱和状态。同时,入库沙量较原设计值减少60% ,三峡库区的泥沙淤积大大减轻,出库沙量也比原预测的要少70% ,水流明显变清[14]。分析监利站蓄水前后年平均含沙量变化(图3)可知,含沙量变化规律分3个阶段。
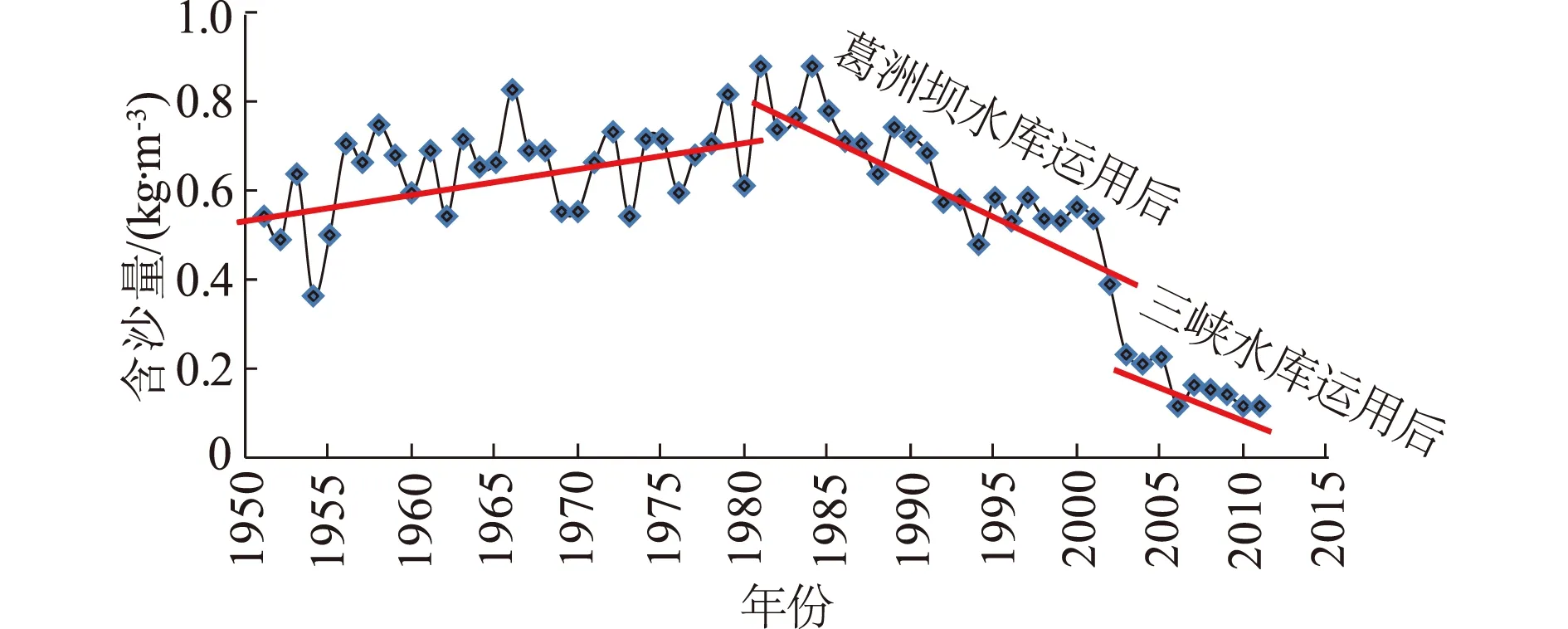
图3 监利站年平均含沙量变化Fig.3 Variation of mean annual sediment concentration in Jianli station
(1) 第1阶段(1950—1980年):监利站含沙量年际变化有增有减,其值围绕着多年平均值0.642 kg/m3上下波动,含沙量整体呈递增趋势。
(2) 第2阶段(1981—2002年):1981年5月葛洲坝水利枢纽开始蓄水,拦蓄了上游水流挟带的部分泥沙,监利河段含沙量呈逐年递减趋势,至2002年监利站含沙量递减至0.393 kg/m3。
(3) 第3阶段(2003至今):2003年三峡水库运用以来,监利河段含沙量大幅降低,2003年递减至0.232 kg/m3。2006年为枯水年,平均含沙量降低至0.118 kg/m3;2007年平均含沙量恢复至0.166 kg/m3。各年平均含沙量递减至0.2 kg/m3以下。
从不同时期各月平均含沙量对比图(图4)可以看出,监利站在三峡蓄水后各月平均含沙量明显低于蓄水前,汛期和枯水期含沙量分配发生改变。蓄水后,河段汛期含沙量占全年比重减少,2002年汛期平均含沙量为0.625 kg/m3,汛期含沙量占全年的81.1%;2003年降低为73.5%,2006年降低为68.5%,2007年降低为77.7%。相应地,枯水期含沙量占全年含沙量的比重增加。
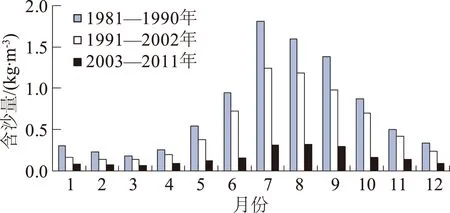
图4 监利站不同时期各月平均含沙量对比Fig.4 Comparison of mean monthly sediment concentration at different periods in Jianli station
2.2 平滩面积对水沙条件的响应
监利河段属于长江中游的冲积性河流,河床演变与河段内的来水来沙条件关系密切。水沙条件的改变会使得河床做出相应的自调整,从而塑造出与之相适应的河床形态,并对应着不同的平滩面积。考虑到长江的年径流量大,含沙量相对较小,本文将以年平均水沙条件作为研究对象。根据监利站实测水沙资料和大断面资料,分析平滩面积与各因子的相关关系,如图5所示。图中,Ab表示平滩面积,Qf表示年平均流量,ζf表示来沙系数。

图5 平滩面积与各因子的相关关系Fig.5 Relationships among bankfull area and different factors
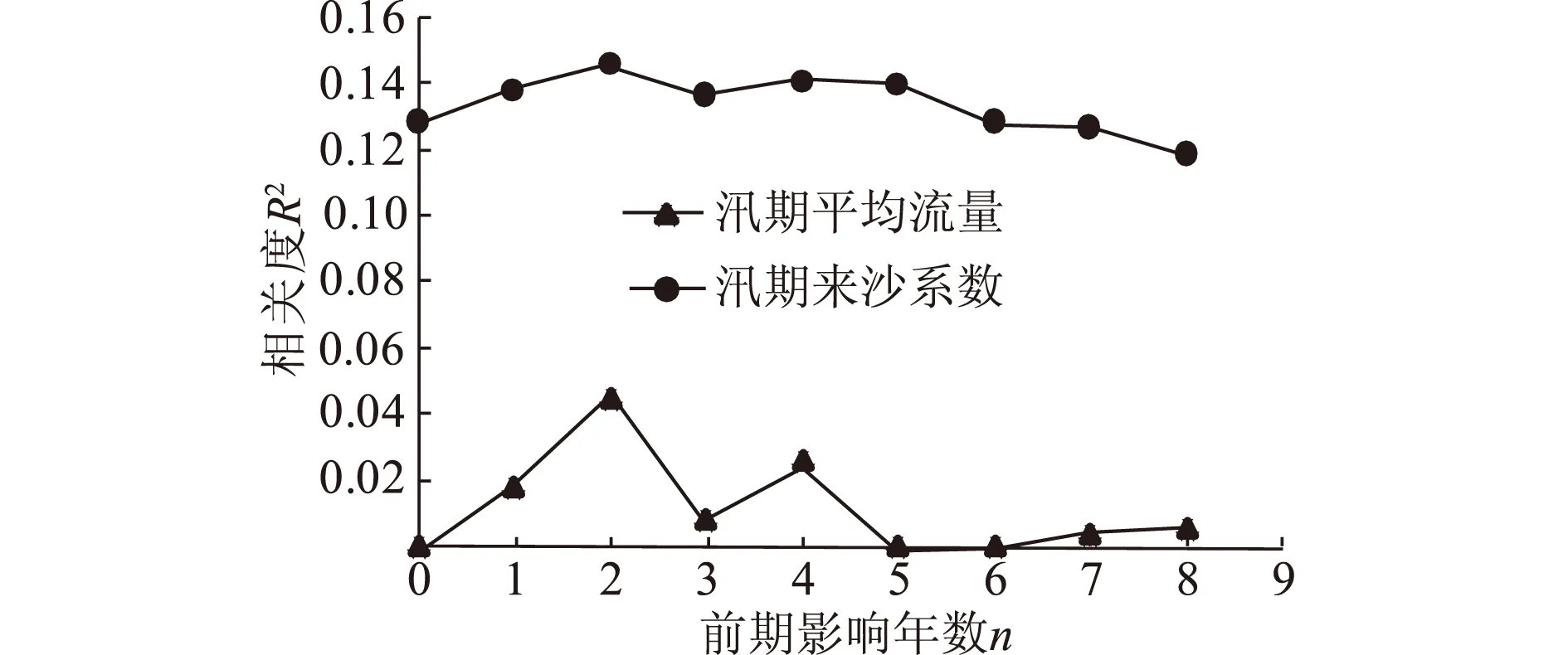
图6 监利站平滩面积与年平均水沙条件滑动平均值的R2变化Fig.6 Variation of R2 between bankfull area and moving average values of mean annual water and sediment factors in Jianli station
由图5和图6可以看出,平滩面积与当年的水沙条件相关性都比较低,但是随着包含的前期影响年数的增加,决定系数R2在受到前期3 a(n=2)内来水来沙条件的影响时取得最大值。监利站平滩面积与当年年均流量的相关度R2为0.000 8,与前期3 a内的年均流量滑动平均值的相关度R2为0.045 3;监利站平滩面积与当年来沙系数的相关度R2约为0.1,与反映年内流量过程参数的1-1/ρ的R2约为0.3。分析表明,随着包含的前期影响年数n的增加,平滩面积与年均流量的相关度R2也在不断增加,但是监利站平滩面积对来沙系数ζf以及反映年内流量过程参数ρ的相关度R2变化不大,因此改进后的滞后响应模型主要考虑流量的不同年影响,将水流来沙系数ζf和反映年内流量过程参数的ρ作为影响因子,其计算成果将在第3节介绍。
3 监利站平滩面积计算
吴保生等[6,15-17]对于冲积河流河床调整中的滞后响应现象进行了大量的研究,并建立了适用于黄河流域的滞后响应理论。李凌云等[18-19]完善了该模型的理论,并在此基础上加以改进,其改进后的模型计算式在黄河流域得到了较好的应用[20-21]。本文利用黄河滞后响应模型进行初步计算,以获得监利站黄河滞后响应模型计算的结果,并使之与改进的模型计算结果进行对比分析。
3.1 滞后响应模型
天然河流系统的来水来沙条件是不断变化的。在一个给定的有限时段Δt内,河道断面不一定能够调整至平衡状态。吴保生[15]基于冲积河流自动调整的基本原理,根据河床在受到外部扰动后的调整速率与河床当前状态和平衡状态之间的差值成正比的基本规律,首先建立了河床演变滞后响应的基本模型。该模型中将河床从原有状态演变到新的平衡状态的过程用以下一阶常微分方程来描述,即
(1)
式中:θ为特征变量(可以是平滩流量Qb或平滩面积Ab);θe为特征变量的平衡值;t为时间;β为系数。
对上式进行积分求解,最终得到在n个时段内河床调整结果的多步递推模式,即
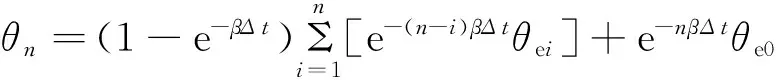
(2)
上式即为滞后响应模型的表达式。该式表明,当前时段的河床演变不仅是当前时段水沙条件的函数,也受前期若干时段内水沙条件的影响,这就是前期影响的实质所在。
李凌云[18]通过引入一维河床冲淤变形方程和不平衡输沙方程推导出了式(2)的基本形式,并在其改进的模型中,将初始时段Ab0的权重调整为(1-eβΔt)e-nβΔt,以消除模型对初始平滩面积的依赖,以及使得前期不同时段水沙条件的影响权重按照时段由近至远时当前权重由大到小的规律分布,由此将式(2)改写为如下形式:
(3)
式(3)即为黄河滞后响应模型。
3.2 黄河滞后响应模型计算
本文收集了监利站1981—2011年实测水沙资料和1975—1987年及2002—2011年实测平滩面积资料。应用黄河滞后响应模型进行计算,并逐步增大前期影响年数n值,其决定系数R2变化如图7所示。由图7可以看出,当n=0时,滞后响应模型的计算精度较低,平滩面积的计算值与实测值之间的R2为0.02。但随着n的增大,模型的计算精度相应提高,并在某一年份取得最大值;当n继续增大,模型的计算精度反而出现递减趋势。由图7还可知,监利站在考虑包含前期3 a(n=2)水沙条件影响时,模型计算值与实测值的精度最高,此时对应的R2为0.11。虽然R2随着计算年数的增加在不断提高,但其相关度仍很低,R2<0.2,计算结果仍属于不相关。
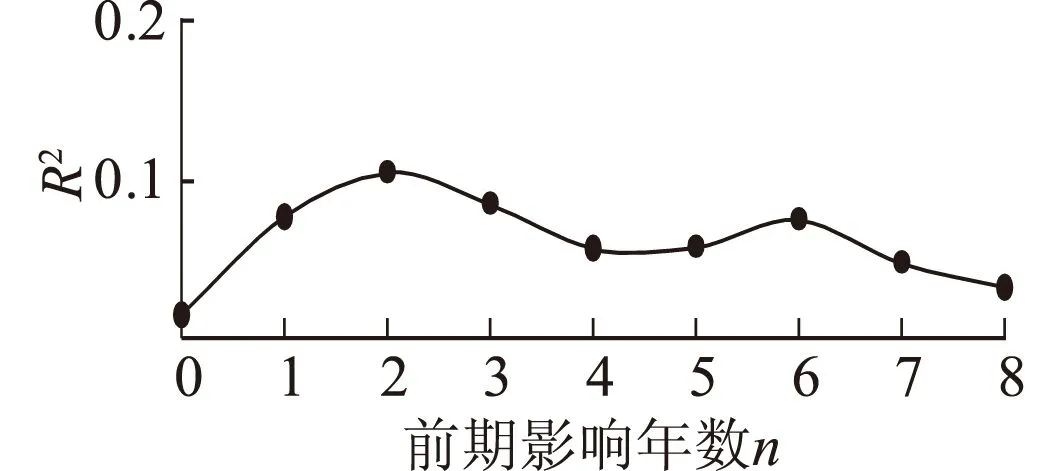
图7 监利站平滩面积计算精度随包含前期影响年数n的变化Fig.7 Variation of computational accuracy of bankfull area in Jianli station with n
由上可知,监利站平滩面积受到前期3 a(n=2)内来水来沙条件的影响较大。此时应用滞后响应模型计算平滩面积时,可取n=2,Δt=1,由此得到适用于监利站的平滩面积计算方程为
(4)
式中:Ab2为考虑前3 a(n=2)内来水来沙条件影响下的平滩面积计算值(m2);εfi为第i年的汛期平均来沙系数(kg·s/m6);Qfi为第i年汛期平均流量(m3/s)。
包含前期影响年数n=3时,由式(4)所得的平滩面积计算值与实测值的历年变化情况及其对比关系如图8所示。由此也可以看出,直接用黄河流域建立起来的滞后响应模型进行计算,其结果并不理想,必须对其进行改进。

图8 平滩面积的计算值与实测值的历年变化及其对比分析(n=3)Fig.8 Comparison analysis of annual variation of calculated value and measured value of bankfull area (n=3)
3.3 改进的滞后响应模型计算
由监利站1981—2011年的实测水沙资料和1975—1987年及2002—2011年的实测平滩面积资料可知,平滩面积的调整对流量的响应明显于对水流含沙量的响应过程。进一步分析可知,上游河段的来水过程对河段断面上的平滩面积调整也有较大的影响。为此,引入年内径流量的绝对变化值ρ作为不同来水过程影响的参数,ρ值越大,表明年内流量的变幅就越大。由此建立的滞后响应模型为
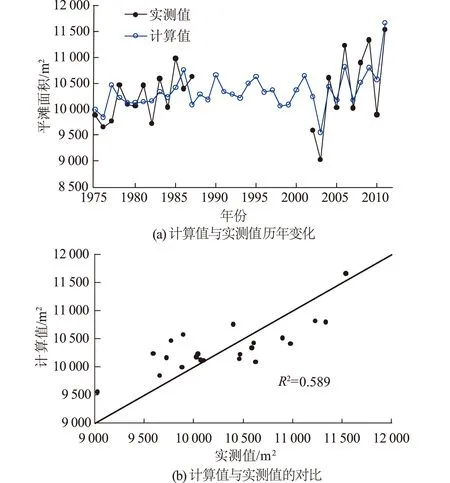
图9 改进后平滩面积的计算值与实测值的历年变化及其对比分析(n=3)Fig.9 Comparison analysis of annual variation of the calculated value by modified model and measured value of bankfull area(n=3)
(5)
式中:ρ为年内径流量的绝对变化值,ρ=Qmax/Qmin,其中Qmax为年内最大日均流量,Qmin为年内最小日均流量;n为滞后响应计算时段,也是前期影响年数;K,a,b,c为相关系数和指数,均是通过实测资料拟合得出。
类似于黄河滞后响应模型的分析,监利站平滩面积受到前期3 a(n=2)内来水来沙条件的影响较大。将改进后的模型应用于监利站,利用所收集的实测水沙资料和实测平滩面积,拟合计算模型中的系数和参数,得到以下计算方程,即
(6)
对比式(6)的计算值与实测平滩面积值,可得到相应的模型计算精度指标R2≈0.6。图9给出了改进后的滞后响应模型计算平滩面积与实测值历年变化情况及其对比分析。 由此可见,相较于直接套用黄河流域建立的模型,改进后的模型计算成果更符合监利站断面平滩面积的调整模式。改进后的模型计算值及其变化趋势都与实测值较为相符,模型计算值与实测值的相关度R2也显著提高,由开始的0.11提高到0.6。从图9(a)也可以发现,模型计算值与实测值的变化规律也较为一致。因此,改进后的滞后响应模型,其计算结果比未改进的计算模型更符合荆江河段的计算。计算值与实测值的相关度R2在区间[0.5,0.8]内,计算成果属于显著相关。
4 结 论
(1) 监利站为荆江河段水沙特征的代表站,处于长江中游,其水量丰富,年径流量大,但水流含沙量较小。分析可知,监利站的水沙条件变化主要源于上游水利枢纽的建立。河段内大型水库的建成,削减了径流过程中的洪峰流量,加大了枯水流量,使得径流年内变化趋于稳定;水利枢纽对水流含沙量的影响更为突出,由于上游来沙中的大量推移质以及悬移质中较粗的部分拦在库内,同流量下出库含沙量显著减小。
(2) 分析表明,通过选用平滩面积参数分析河床形态对水沙条件的响应,监利河段的前期来水来沙条件对当前平滩面积调整的影响真实存在,平滩面积的滞后响应现象在监利站得到了验证,其滞后响应年数为3 a(n=2)。
(3) 通过对比黄河滞后响应模型和改进后的平滩面积模型的计算成果可知,改进后的模型更能符合实测的调整过程,其模型计算值与实测值的相关度R2也显著提高,监利站的相关度R2由0.11提高到0.6,计算成果由不相关提高为显著相关。
(4) 相较于在黄河流域建立的滞后响应模型,改进的滞后响应模型中不仅考虑了水沙条件对平滩面积调整的影响,也引入了年内径流的变化作为不同来水过程的影响。同时,不同于黄河,长江流域水多沙少,因此改进的滞后响应模型只将来沙系数作为影响因子,且只考虑了流量在相应影响年内的滞后响应。实践证明该改进使得模型计算精度提高明显。
(5) 本研究对滞后响应理论在长江上的应用进行了初步探索,其精度仍然不高。由于天然河流的河床调整极其复杂,影响因子众多,监利站改进后的滞后响应模型仍然为概化的计算模型,如何全面考虑各个影响因子以及提高模型的计算精度还需要进一步的分析和研究。
[1] 谢鉴衡.河床演变及整治[M]. 北京:中国水利水电出版社,1990.
[2] LEOPOLD L. B,MADDOCK T. The Hydraulic Geometry of Stream Channels and Some Physiographic Implications[R]. United States Geological Survey Professional Paper, 1953:57.
[3] 钱 宁,张 仁,周志德. 河床演变学[M]. 北京:科学出版社,1987.
[4] HOOKE J M. River Channel Adjustment to Meander Cutoffs on the River Bollin and River Dane, Northwest England[J]. Geomorphology, 1995, 14(3): 235-253.[5]SURIAN N,RINALDI M.Morphological Response to River Engineering and Management in Alluvial Channels in Italy[J]. Geomorphology,2003,50(4): 307-326.[6] 吴保生,游 涛. 水库泥沙淤积滞后响应的理论模型[J]. 水利学报,2008,39(5):627-632.
[7] 梁志勇,杨丽丰,冯普林. 黄河下游平滩河槽形态与水沙搭配之关系[J]. 水力发电学报,2005,24(6):68-71.
[8] 冉立山,王随继. 黄河内蒙古河段河道演变及水力几何形态研究[J]. 泥沙研究,2010,(4): 61-67.
[9] 胡春宏,陈建国,刘大滨,等. 水沙变异条件下黄河下游河道横断面形态特征研究[J]. 水利学报,2006,37(11):1283-1289.
[10]许炯心. 黄河下游洪水的输沙效率及其与水沙组合和河床形态的关系[J]. 泥沙研究,2009,(4):45-50.
[11]HUANG H Q. Reformulation of the Bed Load Equation of Meyer-Peter and Müller in Light of the Linearity Theory for Alluvial Channel Flow[J]. Water Resources Research, 2010, 46: W09533.
[12]刘晓芳,黄河清,邓彩云. 冲积河流稳定平衡条件与断面几何形态的数理分析[J]. 泥沙研究,2012,(1):14-22.
[13]蔺秋生,黄 莉,董耀华. 监利水文站年径流序列多时间尺度分析[J]. 水文,2009,29(4):64-67.
[14]许全喜. 三峡工程蓄水运用前后长江中下游干流河道冲淤规律研究[J]. 水力发电学报,2013,32(2):146-154.
[15]吴保生. 冲积河流河床演变的滞后响应模型——Ⅰ模型建立[J]. 泥沙研究,2008,(6):1-7.
[16]吴保生. 冲积河流河床演变的滞后响应模型——Ⅱ模型应用[J]. 泥沙研究,2008,(6):30-37.
[17]吴保生,张原锋,夏军强. 黄河下游高村站平滩面积变化分析[J]. 泥沙研究,2008,(2):34-40.
[18]李凌云. 黄河平滩流量的计算方法及应用研究[D]. 北京:清华大学,2010.
[19]李凌云,吴保生. 平滩流量滞后响应模型的该进[J]. 泥沙研究,2011,(2):21-26.
[20]李凌云,吴保生. 渭河下游平滩流量的预测[J]. 清华大学学报(自然科学版),2010,50(6):852-856.
[21]李凌云,吴保生,侯素珍. 滞后响应模型在黄河内蒙古河段的应用[J]. 水力发电学报,2011,30(1):70-77.
(编辑:黄 玲)Delayed Response of Bankfull Area Due to Variations ofWater and Sediment in Jianli Station
LIAO Zhi-qi1,2,FAN Bei-lin1,LI Ling-yun1,WANG Jia-sheng1,WANG Jun-zhou1
(1.Key Laboratory of River Regulation and Flood Control of Ministry of Water Resources,Yangtze River Scientific Research Institute,Wuhan 430010,China;2.Ganzhou Survey and Design Institute of Water Conservancy and Hydropower, Ganzhou 341000,China)
It has been proved by analyzing the field data that the adjustment of riverbed in alluvial river is delayed due to variations of water and sediment load. In this paper, Jianli station in Changjiang river was selected as the research object. Through analyzing process and characteristics of delayed response of the bankfull area of Jianli station, we explore the regularity of area regulation response, and establish a delayed response model, which is suitable for the regularity. The results show that, influence of incoming water and sediment of Jianli station at early period on current bankfull area’s regulation really exists, and the delayed response theory can also be used to Jianli station, located at Jingjiang segment, Changjiang river. Meanwhile, after improving the delayed response model for Yellow river, we establish the modified delayed response model of bankfull area for Jianli station.
variations of water and sediment; alluvial river; Jianli hydrological station; bankfull area; delayed response; riverbed evolution
2014-07-17;
2014-10-12
国家自然科学基金项目(51209015,51339001)
廖治棋(1989-),男,江西南康人,硕士研究生,主要从事水力学及河流动力学研究,(电话)027-82926172(电子信箱)cky_liaozhiqi1989@163.com。
10.11988/ckyyb.20140591
2016,33(01):1-5,9
TV148
A
1001-5485(2016)01-0001-05

