干式铁心电抗器结构参数对损耗的影响

徐林峰, 徐晓东, 毛启武, 欧小波, 马志钦, 朱东柏

(广东电网有限责任公司电力科学研究院, 广州 510600;2.哈尔滨理工大学 电气与电子工程学院, 哈尔滨 150080;3.明珠电气有限公司, 广州 511400)



干式铁心电抗器结构参数对损耗的影响

徐林峰1, 徐晓东2, 毛启武3, 欧小波1, 马志钦1, 朱东柏2

(广东电网有限责任公司电力科学研究院, 广州 510600;2.哈尔滨理工大学 电气与电子工程学院, 哈尔滨 150080;3.明珠电气有限公司, 广州 511400)

针对上下移动电抗器线圈和改变气隙分布可使电抗器损耗变化20%以上这一现象,用ANSYS软件对干式铁心电抗器的磁场进行了分析,得出线圈涡流损耗与铁心电抗器结构的关系,并提出了设计电抗器铁心时应考虑安匝平衡,以降低铁心电抗器的损耗。通过电磁场计算,分析了铁饼高度与气隙长度对线圈涡流损耗的影响程度,得出合理的铁饼高度和气隙长度的范围,可为今后电抗器设计提供参考。

ANSYS;安匝平衡;干式铁心电抗器;涡流损耗

根据一些企业使用铁心电抗器的反馈结果,上下移动电抗器线圈可使电抗器损耗变化20%以上,改变气隙尺寸也可使电抗器损耗变化接近20%[1]。通常铁心电抗器夹件引起的附加损耗仅占总损耗的2%～4%[2-3],而由于铁心与线圈布局不合理产生的附加损耗可使总损耗增加20%～30%。根据对铁心电抗器磁场的计算与分析,铁心心柱中的气隙大小、气隙与铁饼的关系、气隙布局与线圈的关系都会对铁心电抗器的损耗产生较大的影响。本文用ANSYS软件对干式铁心电抗器的结构进行磁场计算,从而得出了结构参数对铁心电抗器涡流损耗的影响。

1 铁心电抗器的磁场分布

铁心电抗器铁心中的磁通是由外部线圈产生的,铁心被看成良好的导磁体,而磁阻主要来自气隙[4]。为降低附加损耗,铁心柱有若干个气隙与铁饼组成,每个铁饼中的磁场取决于与之相关线圈的安匝数,如图1所示。当每部分安匝数相同,即IW1=IW2=IW3时,相对应铁心部分的磁场近似相等,因此空间磁场不会存在跳过铁饼绕行,故空间漏磁较小,空间漏磁引起的附加损耗较小。当铁饼中的磁场与铁轭连接伸入线圈部分铁心中的磁场不一致时,空间漏磁场会增大,从而造成附加损耗增大。因此,合理的铁心电抗器结构应考虑铁饼与铁心的安匝平衡。为了便于论述,本文将铁心柱中的铁饼称之为铁饼,将铁心伸入线圈部分称之为柱铁。在ANSYS仿真中,采用轴对称(Axisymmetric)模型,场域为铁心窗体部分。除轴外,均为第二类边界条件[5]。

图1 铁心电抗器的安匝平衡

1.1 柱铁高度与铁饼的关系

铁心电抗器的气隙结构结构与磁场分布如图2所示。

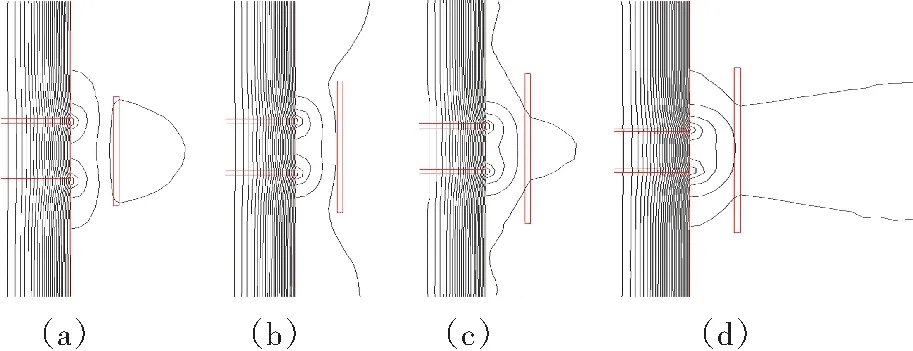
图2 柱铁高度变化引起的空间磁场变化

图2(a)是柱铁高度为铁饼高度2/5时的空间磁场分布。由于柱铁对应的安匝数小于铁饼对应的安匝数,使得部分磁力线不通过铁心构成回路。因此,空间漏磁较大,线圈涡流损耗较大。其特点为线圈端部涡流损耗较大,易发热。中部铁饼损耗较大,温度较高。图2(b)为柱铁高度是铁饼高度4/5时的空间磁场分布。柱铁对应的的安匝数与铁饼对应的安匝数接近,空间漏磁与上下轭铁构成回路,磁力线在线圈端部弯曲程度减轻,因此线圈的涡流损耗减小,其结构相对图2(a)更合理。图2(c)为柱铁高度为铁饼高度6/5时的空间磁场分布。此时,柱铁对应的安匝数略大于铁饼对应的安匝数,空间磁力线有跨过铁饼的趋势,空间磁场在线圈中部穿过,造成线圈中部涡流损耗增加,其特点为线圈中部较热。上下柱铁的磁通大于中间铁饼的磁通,故易发热。图2(d)为柱铁高度为铁饼高度8/5时的空间磁场分布。柱铁对应的安匝数远大于铁饼对应的安匝数,此时磁力线跨过线圈的趋势增加,表明中部空间漏磁较大,造成线圈中部损耗增加,使得线圈中部发热明显。由于跨过铁饼的磁力线增多,上下柱铁更易发热。

选取一个铁饼,铁饼高度为50 mm,气隙长度为5 mm,铁轭到线圈距离为90 mm,导线的宽厚比为3,其涡流损耗倍数与柱铁高度关系如图3所示。

图3 涡流损耗倍数与柱铁高度的关系

在图3中可以看到,当柱铁高度为40 mm时,线圈的涡流损耗最小。这是由于线圈端部到铁轭距离较大,使得此部分铁心对应少部分的安匝数,因此柱铁高度低于铁饼高度。当柱铁对应的安匝数较小时,线圈端部横向漏磁较大;当柱铁对应的安匝数较大时,线圈中部横向漏磁较大。计算表明当柱铁高的80%时,线圈涡流损耗最小;铁心中磁场分布不均匀将造成硅钢片单位损耗增大3%,该值不随结构尺寸变化而大幅度变化。

1.2 上下柱铁高度不对称对线圈涡流损耗的影响

当上下柱铁高度不同时,柱铁高度小的一端,对应的安匝数较小,无法约束空间磁场返回柱铁,导致对应区域空间磁场增加;柱铁较高的一端,对应的安匝数较大,易于吸引空间磁场返回柱铁,产生跨越铁饼的空间磁场。二者叠加会使得局部空间局部磁场增强,造成线圈涡流损耗增大。上下端柱铁高度不等时空间磁场变化如图4所示。

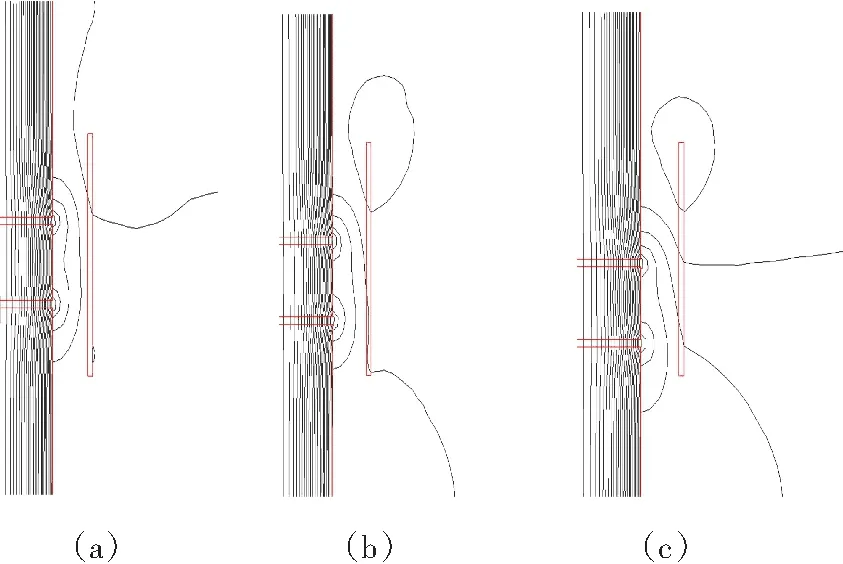
图4 上下端柱铁高度不等时空间磁场变化

图4(a)为上端柱铁55 mm,下端柱铁45 mm时的磁场分布。此时,上、下柱铁高度相差不大,柱铁高度小的一端,空间磁场存在扩散现象。图4(b)为上端柱铁70 mm,下端柱铁30 mm时的磁场分布。图中柱铁高度小的一端空间磁场扩散进一步加强。图4(c)为上端柱铁80 mm,下端柱铁20 mm 时的磁场分布。可见,扩散的磁力线由图4(a)的一根变为三根。根据此磁力线变化可知,随着上、下柱铁高度差值增加,对于柱铁高度小的一端,对应的线圈横向漏磁增加,会产生柱铁高度小的一端对应的线圈涡流损耗增加,温度增加;柱铁高度高的一端,柱铁表面横向磁场集中,损耗较大,温度较高。上下柱铁高度偏差与线圈涡流损耗关系如图5所示。

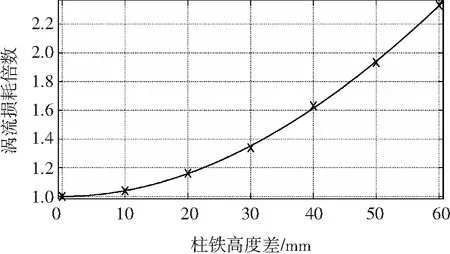
图5 线圈涡流损耗倍数与柱铁高度偏差的关系

由图5可见,线圈涡流损耗倍数随柱铁高度差升高而增大,故在优化电抗器结构时,要考虑使上、下柱铁高度相等。

2 气隙、铁饼与磁场的关系

单个铁饼高度增加会使气隙磁场衍射增加且空间磁场减小,单个气隙长度增加也会使气隙磁场衍射增加,两者都会影响线圈的涡流损耗。因此合理选取铁饼高度与气隙长度,对铁心电抗器的设计非常有意义。

2.1 铁饼高度对线圈涡流损耗的影响

气隙均为5 mm,铁饼高度分别为30、70、90、130 mm的空间磁场分布如图6所示。由图6可见,随着铁饼高度的增加,空间纵向磁场减小,但横向磁场增加。影响涡流损耗的因素一个减小,另一个增加,因此存在一个最优铁饼高度问题,线圈涡流损耗比与铁饼高度的关系如图7所示。

由图7可知,线圈涡流损耗比初始时随铁饼高度的增加而减小,这是由于铁饼高度增加,明显降低纵向漏磁,使得线圈涡流损耗降低[6],即随着铁饼高度增加,气隙导致的磁场衍射范围增大,横向漏磁增加,使得线圈涡流损耗增大,损耗比降低幅度随铁饼高度增加变化趋缓。当铁饼高度继续增加时,横向漏磁场进一步增大,导致损耗比增大。当导线宽厚比增大时,横向漏磁场引起的损耗比变化更加明显,线圈涡流损耗比最小值位置逐渐向左偏移。

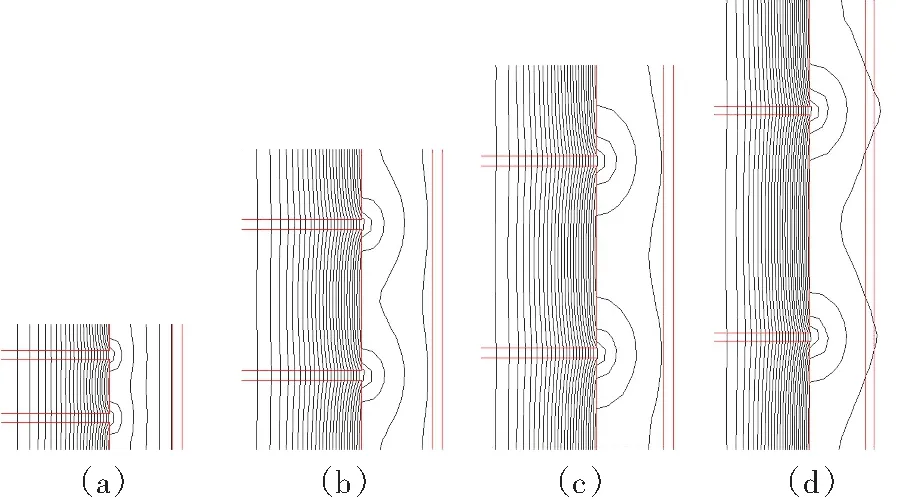
图6 铁饼高度与空间磁场的关系

图7 线圈涡流损耗比与铁饼高度的关系

综上所述,当气隙为5 mm时,铁饼高度宜选择在50～100 mm,线圈宽厚比小于7为佳。

2.2 气隙长度对线圈涡流损耗的影响

随着气隙长度增加,气隙处磁场衍射程度增加,并且空间漏磁增加,同时磁场畸变程度加剧,当铁饼厚度为100 mm时,其变化过程如图8所示。由图8可知,涡流损耗会随着气隙长度的增加而增加,当导线厚度为3 mm,电流密度为2 A/mm2时,气隙长度对线圈涡流损耗占总损耗百分比的影响如图9所示。由图9可知,随着气隙长度的增加,线圈损耗所占百分比也不断增大,且导线宽厚比越大,增大趋势越明显。因此,铁饼高度为100 mm,导线宽厚比为3、5、7时,若要控制线圈涡流损耗占总损耗3%以下,气隙长度分别不宜超过14、10和8 mm。

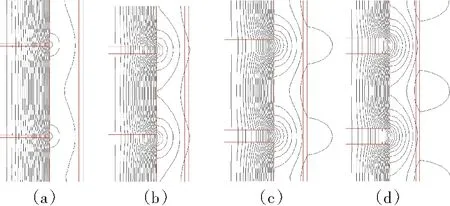
图8 气隙长度与空间磁场的关系

图9 线圈涡流损耗所占百分比与气隙长度的关系

3 结 论

1) 为降低线圈涡流损耗,柱铁与铁饼在设计上要考虑安匝平衡。

2) 合理的铁心电抗器设计应考虑上、下柱铁对应的线圈高度相等。

3) 在设计铁心电抗器时,上、下柱铁高度选择铁饼高度为4/5为佳。

4) 当气隙为5 mm时,铁饼高度宜选择在50～100 mm,线圈宽厚比小于7为佳。

5) 铁饼高度为100 mm,导线宽厚比为3、5、7时,若要控制线圈涡流损耗占总损耗3%以下,气隙长度分别不宜超过14、10和8 mm。

[1] 胡仁喜.ANSYS13.0电磁学有限元分析从入门到精通[M].北京:机械工业出版社.2012.HU Renxi. ANSYS13.0 Electromagnetics finite element analysis[M]. Beijing: China Machine Press, 2012.

[2] 唐兴伦,范群波.ANSYS工程应用教程热与电磁学篇[M].北京:中国铁道出版社,2003.

TANG Xinglun, FAN Qunbo. ANSYS Engineering Application: Thermology and Electromagnetics [M]. Beijing: China Railway Publishing House, 2003.

[3] 程志光,髙桥泽雄,博扎德.弗甘尼.电气工程电磁热场模拟与应用[M].北京:科学出版社,1997.

CHENG Zhiguang, Hashi Sawashio, Bozhade Fuganni. Electromagnetic and thermal field modeling and application in electrical engineering [M]. Beijing: Science Press, 1997.

[4] 王泽忠,全玉生,卢斌先.工程电磁场[M].北京:清华大学出版社,2008.

WANG Zezhong, QUAN Yusheng, LU Binxian. Engineering magnetic field [M]. Beijing: Tsinghua University Press, 2008.

[5] 徐基泰.40年来电抗器技术的发展[J].变压器,2004,21(3):45-49.XU Jitai. Development of reactor technology in recent 40 yea-rs [J]. Voltage, 2004,21(3):45-49.

[6] 周丽霞.磁阀可控电抗器仿真分析及理论研究[D].北京：华北电力大学，2006.

ZHOU Lixia. Simulation analysis and theoretical research on magnetism valve controllable reactor [D]. Beijing: NCEPU, 2006.

(责任编辑 侯世春)

Impact of dry-core reactor structural parameters on losses

XU Linfeng1, XU Xiaodong2, MAO Qiwu3, OU Xiaobo1, MA Zhiqin1, ZHU Dongbai2

(1.Electric Power Research Institute of Guangdong Power Grid Co. Ltd., Guangzhou 510600, China; 2.Electrical and Electronic Engineering Institute, Harbin University of Science and Technology, Harbin 150080, China; 3.Pearl Electric Co., Ltd., Guangzhou 511400, China)

Since moving up and down the reactor coils and changing the distribution of the air gap can change reactor loss of more than 20%, the author used ANSYS software to analyze dry core reactor magnetic field, thus acquired the relationship between coil eddy current losses and core reactor structure, and proposed that balanced ampere-turns should be considered in the design so as to reduce core reactor losses. Through the electromagnetic field calculation, it also analyzed the impact of the discus height and gap length on the coil eddy current loss so as to acquire the range of reasonable discus height and gap length, which provides the reference for reactor design.

ANSYS; ampere-turns balance; dry-core reactor; eddy current loss

2015-05-08。

徐林峰(1957—),男,高级工程师,从事电力系统无功补偿技术研究工作。

TM47

A

2095-6843(2016)01-0073-04