基于平衡补偿法的负载不平衡度测量

李 勇,程汉湘,钟 榜,彭洁锋,阳海彪

(广东工业大学 自动化学院,广州 510006)



基于平衡补偿法的负载不平衡度测量

李 勇,程汉湘,钟 榜,彭洁锋,阳海彪

(广东工业大学 自动化学院,广州 510006)

针对变电站三相电流源出现的不对称负载情况,在基于现有处理方法基础上,提出采用并联补偿装置进行补偿,以求得补偿后系统平衡电流和平衡阻抗,即由不对称负载和补偿电抗的星三角变换对不对称负载进行修正,然后依据补偿前不对称电流等于负载电流为条件重复迭代计算精确求出不对称负载。这样在测出负载不平衡度的同时系统功率因数也得到了补偿。以广东某变电站为例,计算并用Matlab仿真证明了该方法的正确性。

中性点电压;不对称负载;平衡补偿法;并联补偿;Matlab

作为电能质量重要指标之一的“三相不平衡”是针对正常不平衡运行工况而定的[1]。当三相电路中的电源、负载、输电线路阻抗三部分有一部分或几个部分不对称时,电路为不对称三相电路。电力系统正常性三相不平衡主要是由三相负荷不对称所致,电力用户中单相负载在三相系统中的不均衡分配也是导致三相电压不平衡的主要原因之一。文献[2-3]分别采用负荷负序容量与正序容量之比来求负荷电流不平衡度和3个相电压的幅值来求电压不平衡度。这种方法在理论上是可行的,但由于在实际变电站中没有那么多已知量,所以实用性低。文献[4]采用2种谐波(75、125 Hz)电流注入来测量阻抗的方案。这种方法虽然可以精确测量出负载阻抗,但操作十分复杂,在实际的配电站中不可能同时注入不同频率的谐波电流来测量。文献[5]采用对称分量法对不平衡负载进行检测,可以准确测出负载端的变化,但不对称系统得不到补偿。文献[6]在电网电压和阻抗不变的前提下直接利用正序电流注入的方式,并采用递推算法计算电网阻抗,但是电网电压和阻抗的变化降低了递推算法计算的准确性,从而影响了该方法的实用性。文献[7]利用LCL滤波器的谐振特性实现阻抗检测,但检测值为谐振频率下的阻抗值,同时降低了系统稳定性。文献[6-7]只是对三相对称条件下的阻抗检测方法进行了研究,未分析三相电网不对称的情况。针对上述方法存在的缺陷,本文依据变电站实际情况进行了合理假设,分析求得了负载的不平衡程度,并同时得到了并联补偿各电抗的值。

1 平衡补偿原理

不对称系统的运行是电力系统普遍存在的问题。发电机和变压器输出的三相电压或多或少存在不对称,称为电源不对称;负载大小和功率因数的不一致所产生的不对称称为负载不对称。负载电压的不对称现象一般不会太严重,在电能质量中,关注更多的是电流的不平衡。所以本文所讨论的“平衡补偿”是指在三相电压源对称的条件下,通过各种不同的方式使流过电源的三相不平衡电流得到平衡。这种平衡控制的前提条件是,平衡补偿系统不能产生附加的有功损耗。负载自身不对称现象是由负载本身的特性所决定的,也是无法实施平衡控制的。

理论上讲,不对称系统中的平衡补偿目标至少应包含以下几点特征:

1) 补偿后系统的三相线电流幅值相同;

2) 补偿后系统的三相线电流相角相差120°;

3) 在可能的情况下,应尽量使各相功率因数为1;

4) 系统中所有运行设备经平衡补偿后都能稳定工作在额定运行状态;

5) 补偿系统自身不产生任何有功损耗。

负载的不对称无外乎有以下几种表现形式:

1) 三相线路电流幅值相同,功率因数有差异;

2) 线路电流的幅值不同,功率因数各异;

3) 线路电流的幅值不同,功率因数相同。

从三相电路的基本概念出发,任何三相三线制的复杂结构(其中包括负载由多个三角形和多个星形负载的并联结构)的三相负载都可以等效为星形连接的三相负载,而每相负载的等效阻抗均可表示为ZLk=rLk+jxLk,其中k为a、b或c三相线路中的任何一相。对于上面提到的3种不对称表现形式的平衡补偿,最重要的是检测三相等效阻抗中的rLk是否相同,如果相同,则完全可以通过无功补偿的方法得到理想的平衡效果。但以上3种形式的不对称均不能说明三相负载的rLk是否相同,即使检测到的每相负载有功功率相同,但由于系统为不对称运行状态,也不能简单认为各相负载的等效电阻相同。因为在不对称运行条件下,等效星形连接负载的中性点已发生偏移,所以简单地通过线路电流幅值和相位很难直接判断出负载实际阻抗的组成,此时,无功补偿所能起到的平衡作用只能通过具体情况进行分析。准确地讲,只有判断出三相负载的rLk相同,才可能通过无功补偿的方法平衡掉等效阻抗中的xLk,从而实现理想平衡控制。

无论是怎样的不对称表现形式,要实现系统的平衡补偿,一般可采取以下3种形式之一实现平衡控制:

1) 通过幅值和相位均可调节的电流源注入到线路之中,通过电流合成的方法取得线路电流平衡,这种方法一般由在线路上并联的电抗来实现平衡补偿。

2) 在线路中串联一个幅值和相位均可调节的电压源,通过电压的矢量合成改变负载电压的幅值和相位,从而达到三相线路电流的平衡,一般通过电磁耦合的方式得到不同相位电压源。

3) 通过串并联组合方式实现平衡补偿,例如采用独立三相电压输出的统一潮流控制器UPFC来进行平衡补偿控制。

第1种平衡补偿方法的成本最低,可在配电网中广泛推广应用,但补偿所取得的效果必须经过最优运算,本文主要介绍此方法;第2种方法由于主要应用电磁耦合的原理得到不同相位和幅值串联电压源,所需设备的体积较大、质量较重,绕组也比较多,不容易实现精确平衡补偿,但运行的可靠性一般较高;第3种方法是目前比较看好的一种方法,它不仅能实现智能无功的平衡补偿,还能在同一条线路的不同相之间进行有功功率传递,但成本较高。

三相四线制不对称平衡补偿与三相三线制相似,所以本文重点讨论三相三线制平衡补偿。

2 三相三线制不对称系统平衡补偿

在三相三线制配电线路中,沿线负载众多,连接方式错综复杂,有的是星形连接,有的是三角形连接,但无论实际负载是星形连接还是三角形连接,都可以统一转换成星形连接或三角形连接。为方便起见,本文一般先将三角形连接的负载转换为星形连接的方式来进行分析,但负载中性点仍是悬浮的。

2.1 并联电抗平衡补偿

电抗型平衡补偿的实质就是将纯电感或纯电容的各种串、并联结构直接并接在不对称三相系统中,使补偿后的实际运行系统对电源而言近似为对称负荷,最好还能纠正系统的功率因数。欲实现或达到这一目的,要求并接在电路中的电感或电容应该能实现无级变化,这样不仅能对补偿电抗的幅值进行有效控制,还能通过容性和感性变化实现电流方向的改变。从某种意义上来讲,仅通过纯电容或纯电感实现包括有功功率在内的平衡控制是不太可能的,因为阻抗补偿性的补偿支路电流矢量总是与它两端的电压矢量正交,所以通过取线电压或相电压,以及所形成的补偿支路等效中性点的电位偏移,使垂直于电压矢量的补偿电流与负载电流的合成矢量对电源矢量而言能够产生一定范围的相位调节。只要合理地选择补偿支路的感抗或容抗参数,采用最优平衡补偿控制策略,就会使三相电源中的电流不平衡现象得到改善。三相三线制星型负载的补偿结构如图1所示。

图1 三相三线制星型负载的补偿结构

为方便分析计算，将图1中的线路阻抗与负载阻抗合在一起考虑。将三角形连接的负载Zab、Zbc、Zca分别转换为星形连接的三相负载ZLa、ZLb和ZLc,且它们的幅值和相位均不相同。对负载之所以进行这样的转换,主要是为了能方便地获取负载中性点的电位偏移信息,以分析在不同不对称运行条件下补偿控制得到的补偿效果。为了校正三相三线制的不对称三相负载,假设所采用的三角形连接平衡补偿电抗值分别为xqab、xqbc和xqca(正值为感抗,负值为容抗)。平衡补偿的目标就是为了使三相电源输出的三相电流ia(t)、ib(t)和ic(t)幅值要么相等,要么使这三个电流的相角相同。

三相三线制补偿矢量图如图2所示。该矢量图反映了在某一不对称运行负载下的负载中性点电位的偏移情况。如果按图2所示的负载电流和补偿电流的幅值和相位进行合成,以c相电源电流为例,可得到合成电流如图2中左下角的虚线内的幅值和相位。如果改变各补偿支路的电抗幅值,则仍有可能通过电抗性器件的串并联合成效果来满足基本平衡的条件,即使不能得到较为理想的平衡补偿效果,也能够进行最优的平衡补偿控制,使之接近对称运行的条件。

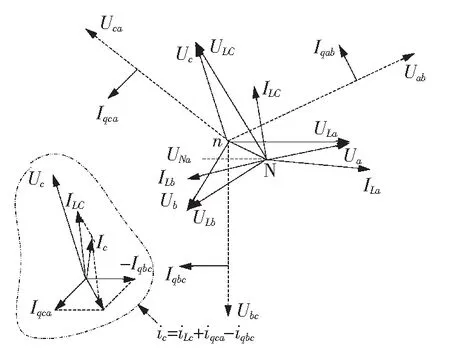
图2 三相三线制补偿矢量图

2.2 三相电源电流数学模型的建立

由图1根据KCL可得三相电源电流的表达式为

(1)

式中:星形三相负载的等效阻抗分别为ZLa=rLa+jxLa=zLa∠φLa;ZLb=rLb+jxLb=zLb∠φLb;ZLc=rLc+jxLc=zLc∠φLc。根据基尔霍夫电流定律可得负载中性点对电源中性点的电压为

(2)

负载中性点的电压矢量还可以按a、b、c三个不同的相电压矢量分别表示为

(3)

式中:yNLa=y1a/yΣ;φNLa=φ1a-φΣ;yNLb=y1b/yΣ;φNLb=φ1b-φΣ;yNLc=y1c/yΣ;φNLc=φ1c-φΣ。

将式(3)代入式(1)中并整理得

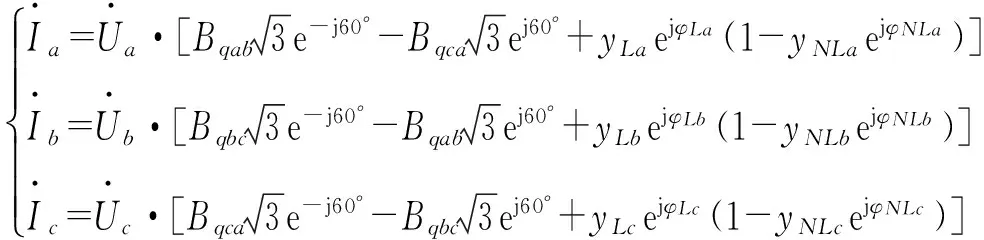
(4)

式中:Bqab=1/xqab,Bqbc=1/xqbc,Bqca=1/xqca。

在式(4)中,将各相电压矢量直接转换为以a相电压矢量所标示的形式,并令a相电压的初相角为零,即可得到各相电源电流的复数表达式:

(5)

根据上文给出的补偿目标的第一和第二点可列方程:

(6)

式(6)为4个方程3个未知数,可以根据最小二乘法求最优解得并联补偿电纳Bqab、Bqbc、Bqca的值,从而可以根据所得参数设计出并联补偿装置。

3 负载不平衡度计算

在变电站中一般已知三相电压以及三相功率潮流,不能测出负载端中性点偏移电压,而建立并求解三相电源电流数学模型的前提是必须已知中性点偏移电压。由图1可知补偿前负载端的电流不变且等于三相电源端补偿前电流,即

(7)

由于不对称负载阻抗和负载中性点偏移电压均未知,但可以猜想在该不对称三相电流情况下存在对应的不对称负载ZLK,使得此中性点电压UNn=0。代入式(1)并建立式(5)三相电源电流数学模型,根据式(6)求出并联电抗数值xqab、xqbc和xqca以及三相电源平衡电流值Ik。

将图1的负载经星三角变换得到图3,再将各相补偿电抗与各相负载阻抗并联得到图4,最后将所得负载经星三角变换得到图5,其阻抗计算表达式为

(8)

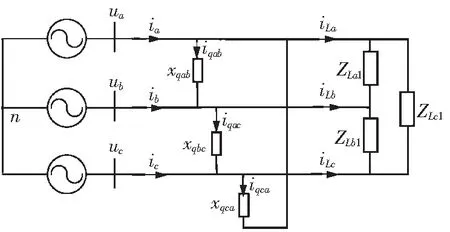
图3 负载变为三角形

图4 负载与补偿电抗并联

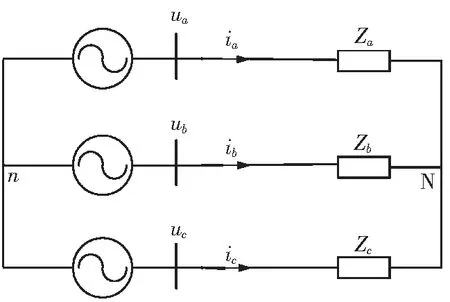
图5 整体对称星型负载

根据上述星三角变换的逆过程可以求出图1中ZLa、ZLb、ZLc,代入式(2)可得在此不对称负载时的负载中性点电压UNn,此时的负载电流为

(9)

与式(7)比较,若电流不相等则根据所求的ZLk、UNn重复迭代计算,直到满足式(7)。具体编程迭代流程如图6所示。此时输出的不对称负载ZLk接近于实际负载端阻抗值,从而测出了负载不平衡度。

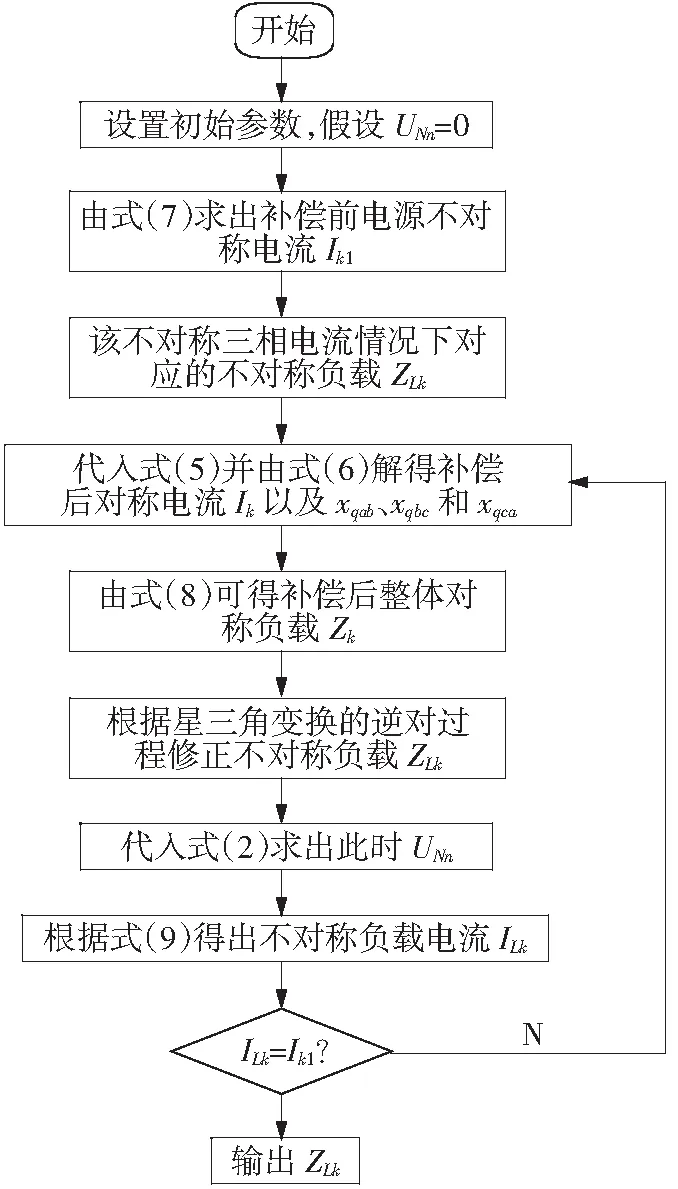
图6 负载阻抗迭代流程图

Fig.6 Load impedance iteration flow chart

4 算 例

广东某35 kV大型企业专用线路的设计容量为10 MVA,采用三相三线制传输方式。在某一时段变电站所测得的a、b、c三相的有功潮流数据分别为1.2 MW、2.3 MW、1.68 MW,无功功率分别为滞后的0.23 MVar、0.31 MVar、1.22 MVar,实时测得的三相电压均为35.6 kV。现要在该变电站设计出并联电抗补偿装置对其进行平衡补偿,并要测出负载不平衡程度。

由式(7)可得补偿前不对称电流为

猜想在该不对称三相电流情况下存在对应的不对称负载ZLK,使得此中性点电压UNn=0，则

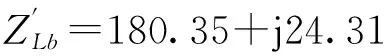
代入式(5)得

Iar=20.55×(0.866Bqab-0.866Bqca+4.34),A

Ibr=20.55×(-0.866Bqab-1.732Bqbc-0.37),A

Icr=20.55×(0.866Bqca+1.732Bqbc+2.025),A

Iaj=20.55×(1.5Bqca+1.5Bqab-0.79),A

Ibj=20.55×(-1.5Bqab+2.34),A

Icj=20.55×(-1.5Bqca-7.76),A

由式(6)解最小二乘法求最优解得补偿电抗为Zqab=j640 Ω;Zqbc=j1.01·1019Ω;Zqca=j7900 Ω。同时求得平衡补偿后电流为

代入式(8)得补偿后整体对称负载为

Za=Zb=Zc=195.22∠37.035°,Ω。根据上文的流程图编程迭代最终求得不对称负载为

ZLa=249.44-j13.93,Ω

ZLb=239.12+j1.4537,Ω

ZLc=122.13+j175.96,Ω

依据变电站的实际数据以及所得参数,使用Matlab仿真得到平衡补偿后各电流波形如图7所示。

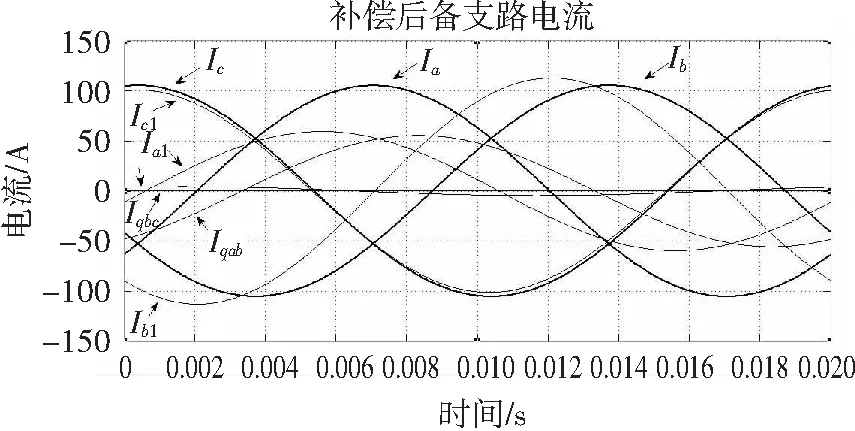
图7 平衡补偿后各电流波形

5 结 语

在变电站中,一般已知三相电压以及三相功率潮流,但未知负载的不平衡程度,也测不出负载端中性点偏移电压。因此,本文根据有限的条件加上合理的假设精确求出了各相负载的阻抗值,同时得出并联补偿电抗的参数值,使得系统功率因数也得到了很好补偿。案例分析表明,该方法可以达到较为理想的效果,且并联电抗平衡补偿方法的成本较低,可在配电网中推广应用。

[1] 肖湘宁. 电能质量分析与控制[M]. 北京:中国电力出版社,2004.

XIAO Xiangning. Power quality analysis and control [M]. Beijing: China Electric Power Press, 2004.

[2] 同向前,王海燕, 尹军. 基于负荷功率的三相不平衡度的计算方法[J].电力系统及其自动化学报,2011,32(2):24-30.

TONG Xiangqian, WANG Haiyan, YIN Jun. Calculation method of three phase unbalance based on load power [J]. Power System and Its Automation, 2011,32(2): 24-30.

[3] 张有玉,郭珂,周林,等. 三相三线制系统电压不平衡度计算方法[J].电网技术,2010,4(7):123-128.

ZHANG Youyu, GUO Ke,ZHOU Lin, et al. Voltage unbalance of three-phase three wire system [J]. Power System Technology, 2010,4(7): 123-128.

[4] 蔡文,刘邦银,段善旭,等. 三相不对称条件下的电网阻抗检测方法[J].中国电机工程学报,2012,32(18):37-42.

CAI Wen, LIU Bangyin,DUAN Shanxu, et al. Method of impedance measurement for three phase asymmetric conditions [J]. Chinese Journal of Electrical Engineering, 2012,32(18): 37-42.

[5] 邹文学,庞兵,陈庆国. 非线性电力系统中对称分量法的应用[J].电机与控制学报,2011,5(5):83-88.

ZOU Wenxue, PANG Bing, CHEN Qingguo. Application of in nonlinear power system in the application of symmetrical component method[J]. Motor and Control Journal, 2011,5(5): 83-88.

[6] COBRECES S,BUENO J,PIZARRO D.Grid Impedance monitoring system for distributed power generation electronic interfac-es [J]. IEEE Transactions on Instrumentation and Measurement,2009,58(9): 3112-3121.

[7] LISERRE M,BLAABJERY F,TEODORESCU R.Grid impedance estimation via excitation of LCL-filter resonance [J].IEEE Transactions on Industry Applications,2007,43(5):1401-1407.

(责任编辑 郭金光)

Measurement of load imbalance degree based onbalance compensation method

LI Yong, CHENG Hanxiang, ZHONG Bang, PENG Jiefeng, YANG Haibiao

(Faculty of Automation,Guangdong University of Technology,Guangzhou,510006,China)

For stubstation three-phase current source of asymmetric load. Based on the existing processing method based on, the author uses parallel compensation device to compensate, to obtain compensation system balancing current and impedance balance, namely asymmetric load and compensation reactance of star delta transformation of asymmetric load correction, and then on the basis of compensation of asymmetric current is equal to the load current conditions are repeated iteratively calculated accurately calculate unsymmetrical load. In this way, the system power factor is compensated by the load imbalance degree. Based on the case of a substation in Guangdong, the correctness of the method is proved by Matlab simulation.

neutral point voltage; asymmetric load; balance compensation method; parallel compensation; matlab

2015-07-21。

李 勇(1991—),男,硕士研究生,研究方向为电力系统及其自动化。

TM714.3

A

2095-6843(2016)01-0023-05