基于公共信息模型拓扑收缩的合环电流计算方法

裴星宇,梁志鹏,彭显刚,翁奕珊

(1. 广东电网有限责任公司珠海供电局,广东 珠海 519000;2.广东工业大学 自动化学院,广州 510006)



基于公共信息模型拓扑收缩的合环电流计算方法

裴星宇1,梁志鹏2,彭显刚2,翁奕珊1

(1. 广东电网有限责任公司珠海供电局,广东 珠海 519000;2.广东工业大学 自动化学院,广州 510006)

针对目前离线的合环研究缺乏时效性的问题,提出了一种配电网在线合环电流计算方法,即利用主网公共信息模型(CIM)数据和SCADA系统实时数据,对主网进行实时拓扑分析,实现节点归并、网络收缩,形成一个实时环网计算模型。同时,以该模型为基础,采用状态估计方法,解决实时数据量测误差影响合环母线电压相角计算精度的问题。经案例应用验证,该方法准确、有效,且为地区电网在线合环辅助决策系统的开发提供了理论依据。

CIM模型; 开关状态; 状态估计; 合环电流

国内城市电网主要采用环网结构、开环运行的方式[1]。当线路需要检修或发生故障时,为了保证供电可靠性,需要进行带电合环操作实现负荷转移。

目前对配电网带电合环操作的研究主要分为离线合环研究和在线合环研究。文献[2-5]主要介绍了离线状态下的合环研究,其研究成果为电力部门合环操作提供了参考依据,但是由于离线合环计算需要运行操作人员手工操作,缺乏时效性,无法反映电网实时运行状态,其计算结果实用性较为局限。因此基于CIM模型的在线合环电流计算方法研究则成为当前合环研究的重点。文献[6]详细阐述了基于CIM 模型的拓扑分析的过程。文献[7]提出了一种基于CIM模型拓扑收缩的方法。文献[8-9]介绍了基于CIM模型的合环软件的设计方案。但这些基于CIM模型的拓扑分析方法和方案并没有应用于实际工程中。因此,本文提出一种在线合环电流计算方法,该方法利用CIM模型的网络拓扑关系,结合SCADA系统提供的在线开关遥信状态,对合环母线两侧的网络进行动态拓扑分析,并对复杂的CIM模型进行拓扑收缩,形成一个实用的实时环网计算模型。同时,针对SCADA系统提供的实时数据存在量测误差且个别环网设备实时数据缺失的问题,采用状态估计的方法进行合环母线电压相角计算,从而实现实时的环网稳态电流计算。

1 CIM模型简介

公共信息模型描述了电力系统生产过程涉及到的各类对象,并用对象类和属性及其之间的关系来描述电力系统资源[10]。各类之间通过简单关联、泛化和聚合相互联系在一起[11]。CIM模型中的电网对象模型，主要包括电力设备模型、连接关系模型。电力设备模型是指电力网络中的一次元件模型,包括线路、母线、变压器等，所有的设备实体类均继承于设备类。连接关系模型由CIM模型中定义的端点和连接点模型来表示。导电设备具有不同数量的端点,例如线路和开关有两个端点,而发电机和变压器绕组只有一个端点。连接节点是指这些节点上的导电设备的端点通过零阻抗连接在一起的节点。一个连接节点可以连接几个端点,但是跟导电设备没有直接连接关系。CIM模型的这种导电设备类与端点、连接点之间的连接关系构成了设备之间的电气连接关系。简单电力网络的CIM模型如图1所示。

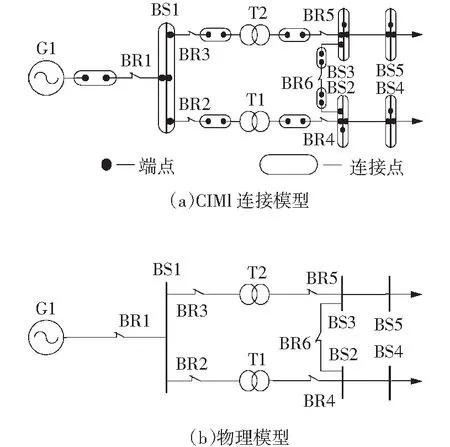
图1 简单电力网络的CIM模型

从CIM模型的解析结果可以看出,根据各对象类的属性及之间的关系,可以通过其“设备——端点——连接点——端点——设备”的电气连接关系,将其转化为物理模型。

2 基于在线开关状态的网络拓扑收缩

在基于CIM模型的配电网合环操作的研究中,由于电网CIM模型数据量大,因此在对合环网络进行拓扑搜索的过程中,需对网架结构进行简化处理。本文提出的基于在线开关状态的网络拓扑收缩方法是利用基于IEC61970标准的CIM模型数据,结合SCADA系统提供的开关位状态信息,通过深度优先算法进行合环网络动态拓扑收缩[12-13]。实现实时网络拓扑收缩的具体步骤如下:

1) 以电源为基本单位,分别进行拓扑分析,即以未遍历的电源点作为遍历起点。

2) 根据CIM模型中的连接关系模型,从电源端点出发搜索端点所属的连接节点,然后根据连接节点搜索连接节点连接的所有端点,即可找到相连的导电设备,根据此方法采用深度优先算法进行搜索。

3) 当遍历到开关设备时,判断开关的状态。若开关闭合,则将闭合的开关设备删除,并以开关的另外一个端点为起点进行遍历,直到搜索到非零阻抗元件,此处形成一个拓扑节点;若开关断开,则此处为开路,按照深度优先算法进行退栈操作。

4) 若遇到闭合开关设备两侧端点所属的连接节点都与母线连接,则两条母线直接相连,并将其合并,既删除其中一条母线。

5) 若遍历到一个未记录(未遍历)的连接节点,此连接节点能搜到导电设备,则形成新的拓扑节点,并按照步骤2)、3)、4)进行拓扑收缩。

6) 查看是否还有未遍历的电源,若全部记录,则拓扑收缩完成,否则,返回步骤1)。

根据上述步骤对图1所示的简单电力网络进行网络拓扑收缩,假设开关BR4断开,其余开关全部闭合,则其拓扑收缩结果如图2所示。

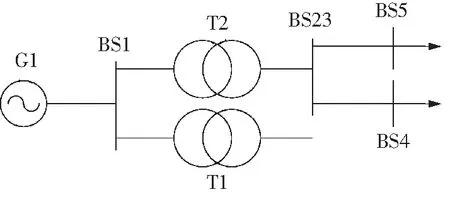
图2 简单电力网络简化模型

Fig.2 Simplified model of simple electric power network

由图2,可以看出,母线联络开关BR6为闭合状态,所以母线BS2和BS3合并为一条母线BS23;开关BR4断开,变压器T1低压侧开路,无法搜到母线BS2,母线BS2与BS3合并,其输出由变压器T2转供。通过此方法进行网络拓扑收缩,不仅可以简化网络的结构,还可以根据实时的开关状态建立与实际电网运行状态相符的计算模型。

3 拓扑收缩方法在实时合环计算中的应用

将基于在线开关状态的拓扑收缩应用于合环网络的搜索,形成由母线、线路、变压器、负荷节点组成的合环计算模型,然后对实时合环网络进行状态估计并计算合环稳态电流。配电网在线合环电流计算整体流程如图3所示。

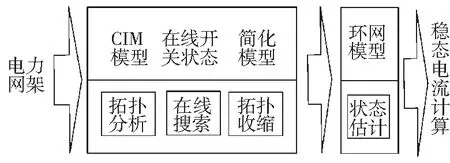
图3 整体流程图

3.1 合环母线电压计算

在电力网架进行拓扑收缩以后,形成的简化网架可以直接进行研究和计算。但是在对配电网实时合环电流计算的研究中,考虑SCADA系统的量测误差和个别环网设备实时数据的缺失,本文通过状态估计的方法对合环母线电压相角进行计算。

基于CIM模型进行拓扑收缩形成的合环网络,其主网结构主要包括两部分:通过网络拓扑收缩形成的两侧10 kV母线到220 kV母线之间的辐射型网络结构;由两侧220 kV母线拓扑收缩形成的网络结构。将主网结构中的220 kV以下电压等级的辐射型网络部分称为内网,220 kV以上电压等级的网络结构称为外网。其中,内网部分各段的等效阻抗可以根据网络拓扑过程中搜索到的CIM模型中的设备类参数进行计算。因而,外网部分的等值计算是状态估计的关键。本文将通过Ward等值法对220 kV电压等级以上的外网进行等值[14-15]。多端口Ward等值网络如图4所示。

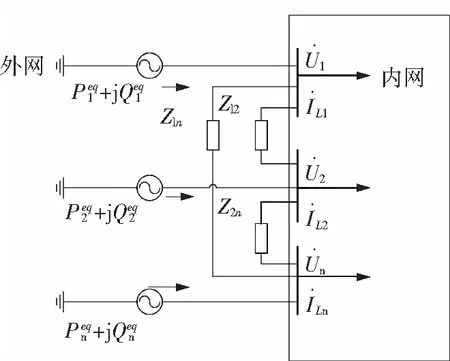
图4 外网Ward等值模型

通过拓扑收缩、等值形成的环网可视为一个小型的电力系统。鉴于最小二乘法状态估计[16-17]的基本算法可以直接用于较小的电力系统,在给定量测系统、支路参数和网络结构的条件下,其非线性量测方程可表示为

z=h(x)+u

(1)

式中,z为m维量测向量;x为n维状态变量向量;u为m维量测误差向量,其服从正态分布。

电力系统状态估计中的量测量主要包括节点电压幅值、支路功率、节点注入功率等。本文将SCADA系统获得环网等值模型中量测设备的实时遥测数据,作为系统的量测量,其量测值可表示为

z=[V1P1Q1P12Q12…VmPmQmPmnQmn]T

(2)

式中,Vm为节点电压幅值量测值,Pm、Qm分别为节点注入有功功率和注入无功功率,Pmn、Qmn分别为支路有功功率和无功功率。

将节点电压幅值和相角作为状态变量,其算术表达式为

x=[V1θ1V2θ2…Vnθn]T

(3)

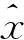
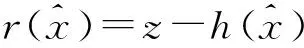
(4)

J(x)=[z-h(x)]TR-1[z-h(x)]

(5)

一般来说,量测函数h(x)为非线性函数。因此通过牛顿法可以得到状态修正方程,即

(6)

(7)

式中,H(x)为m*n阶量测矢量的雅克比矩阵。

按照式(6)对状态量x进行迭代修正,以式(8)为收敛依据,不断迭代直到满足收敛条件。

(8)

3.2 稳态电流计算

配电网合环稳态电流主要包括合环前辐射型网络的馈线电流和合环后形成的环流,其中合环环流的计算是合环稳态电流计算的重点。合环稳态电流计算模型如图5所示。

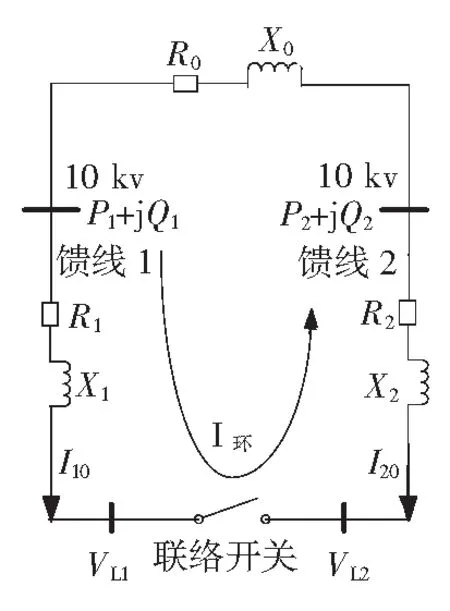
I10和I20——合环点两侧馈线初始电流;VL1和VL2——合环点两侧的电压。

合环开关两侧电压差引起的环流为

(9)

合环后流经馈线1的稳态电流为

(10)

合环后流经馈线2的稳态电流为

(11)

4 应用实例

本文以广东省某市港北站黄茅海线F16馈线与南化站南水线F6馈线的合环联络开关的合环操作为例进行计算,其合环电流计算的系统流程如图6所示。

图6 系统流程图

从图6可以看出,当选定合环开关后,系统将根据本文提出的合环电流计算方法,通过在线环网拓扑收缩、合环网络等值、合环母线电压计算、合环电流计算等步骤,实现合环馈线实时稳态电流的准确计算,并生成实时环网拓扑图，如图7所示。

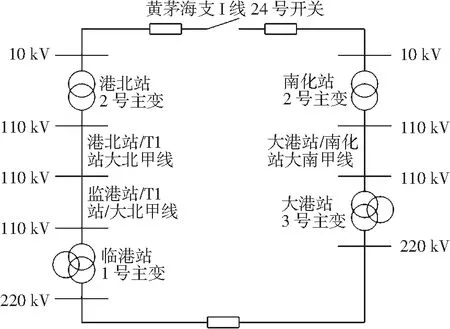
图7 环网拓扑图

Fig.7 Topology architecture of ring network

根据从主网SCADA系统中读取的电网实时遥测数据,通过环网等值模型进行状态估计,其计算结果如表1所示。

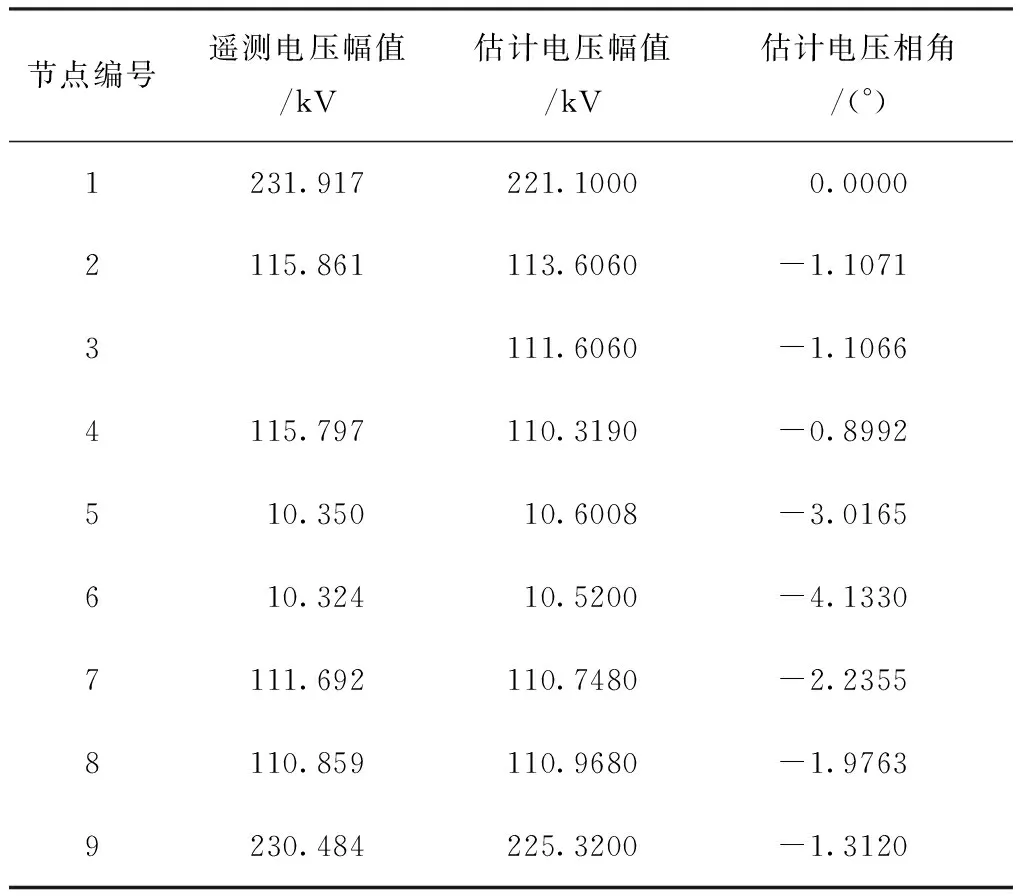
表1 状态估计结果

从表1可以看到,节点3电压数据缺失;节点5为港北站黄茅海线F16的10 kV母线节点,其母线电压幅值和相角分别为10.6008 kV和-3.0165°;节点6为南化站南水线F6的10 kV母线节点,其母线电压幅值和相角分别为10.52 kV和-4.133°。合环电流计算结果如表2所示。

表2 合环电流计算结果

由计算结果可以看出,由于合环开关两侧电压差引起的环流使南化站南水线F6馈线的稳态电流从215.53A增加到270.39A,增加了25.5%((稳态电流-初始电流)/初始电流=(270.39-215.53)/215.53=25.5%),但是合环稳态电流没有超过电流保护整定值,因此可以进行合环操作。

5 结 语

本文提出的利用主网CIM模型和SCADA系统遥信开关状态进行实时拓扑收缩的方法,经案例应用验证,该方法能有效地利用SCADA系统提供在线遥测、遥信数据,其形成的动态模型真实地反应了合环电流计算时间点的实际环网结构;而且对实时网络进行状态估计,既可以对不良遥测数据进行修正,实现合环母线电压相角的计算,又降低了由于不良数据造成的计算误差。

[1] 贺翔, 刘永强， 樊利民. 基于主网CIM的配电网合环潮流计算[J]. 电力系统及其自动化学报, 2011, 23(3): 35-38.

HE Xiang, LIU Yongqiang, FAN Limin. Loop power flow calculation for distribution network based on higher grid CIM [J]. Proceedings of the CSU-EPSA, 2011, 23(3): 35-39.

[2] 邹俊雄, 周冠波, 付轲，等. 10 kV配网合环转电计算模型与试验分析[J]. 电力系统保护与控制, 2010, 33(8): 144-148.

ZOU Junxiong, ZHOU Guanbo, FU Ke, et al. Electromagnetic loop closing calculation model and experimental analysis on 10 kV distribution network [J]. Power System Protection and Control, 2010, 33(8): 144-148.

[3] 叶清华, 唐国庆. 配电网合环操作环流分析系统的开发和应用[J]. 电力系统自动化, 2002, 26(22): 66-69.YE Qinghua, TANG Guoqing. Development and application of the analysis system for closed loop operation of distribution network [J]. Automation of Electric Power Systems, 2002, 26(22): 66-69.

[4] 刘健, 孙泉, 张小庆， 等. 配电网合环分析与合环条件判断[J].电力系统自动化, 2014, 38(11): 130-135.

LIU Jian, SUN Quan, ZHANG Xiaoqing, et al. Analysis on and criteria for loop closing operation for distribution grid [J]. Automation of Electric Power Systems, 2014, 38(11): 130-135.

[5] 将瀚书, 孙崇也, 贾彦兵， 等. 10 kV配电网合环电流暂态过程的分析与仿真[J]. 黑龙江电力, 2011, 33(2): 88-90.

JIANG Hanshu, SUN Chongye, JIA Yanbing, et al. Transient analysis and simulation of surge current due to closing loop in 10 kV distribution network [J]. Heilongjiang Electric Power, 2011. 33(2): 88-90.

[6] 陈根军, 顾全. 基于CIM的配电网一体化追踪拓扑[J].电力系统自动化, 2009, 33(3): 59-63.

CHEN Genjun, GU Quan. A CIM-based integrative network-tracing method for power distribution systems [J]. Automation of Electric Power Systems, 2009, 33(3): 59-63.

[7] 廖怀庆, 刘东, 黄玉辉， 等. 基于公共信息模型拓扑收缩的配电网转供能力分析[J]. 电网技术, 2012, 36(6): 51-55.LIAO Huaiqing, LIU Dong, HUANG Yuhui, et al. Analysis on transfer capability of distribution network based on CIM topological contraction [J]. Power System Technology, 2012, 36(6): 51-55.

[8] 钱兵, 程浩忠, 杨镜非， 等. 电网合环辅助决策软件研究[J]. 电力系统自动化, 2002, 22(3): 8-11.

QIAN Bing, CHENG Haozhong, YANG Jingfei, et al. Research on object-oriented and visual assistant decision-making software for power system linkage [J]. Automation of Electric Power Systems, 2002, 22(3): 8-11.

[9] 陈清鹤, 刘东, 李荔芳. 基于CIM建模的配电网三相潮流计算[J]. 电力系统自动化, 2005, 29(23): 49-53.

CHEN Qinghe, LIU Dong, LI Lifang. CIM based three-phase power flow for distribution systems [J]. Automation of Electric Power Systems, 2005, 29(23): 49-53.

[10] 娄宗明, 章坚民. 基于在线开关状态和 DG 角色的动态配电网拓扑分析[J]. 电力系统保护与控制, 2014, 42(13): 64-69.

LOU Zongming, ZHANG Jianmin. Dynamic topologic analysis of distribution network based on on-line switch and DG states [J]. Power System Protection and Control, 2014, 42(13): 64-69.

[11] Draft IEC61970, Energy management system application program interface Part 301: Common Information Model Base[S].

[12] ALAN W. MCMORRAN, GRAHAM W. Ault. Translating CIM XML Power System Data to a Proprietary Format for System Simulation[J]. IEEE Transactions on Power Systems, 2004: 229-234.

[13] 李盟, 秦立军, 郭庆， 等. 基于CIM模型的电网拓扑分析[J].电力科学与工程, 2011, 27(9): 18-22.

LI Meng, QIN Lijun, GUO Qing, et al. CIM-based Network Topology Analysis [J]. Electric Power Science and Engineering, 2011, 27(9): 18-22.

[14] 余娟, 朱柳, 颜伟, 等. 基于内网实测信息的多端口外网静态等值方法[J]. 电力自动化设备, 2013, 33(6): 32-36.

YU Juan, ZHU Liu, YAN Wei, et al. Static equivalence of external multi-port network based on measured information of internal network [J]. Electric Power Automation Equipment, 2013, 33(6): 32-36.

[15] 颜伟, 李世明, 陈俊, 等. 基于内网实测信息的两端口外网静态等值参数估计方法[J]. 中国电机工程学报, 2011, 31(13): 101-106.

YAN Wei, LI Shiming, CHEN Jun, et al. Parameter estimation for two-port external network static equivalent model on the basis of internal network measured information [J]. Proceedings of the CSEE, 2011, 31(13): 101-106.

[16] 于尔铿. 电力系统状态估计[M]. 北京: 水利水电出版社,1985.

YU Erkeng. State estimation of power system [M]. Beijing: WaterPower Press, 1985.

[17] 任轲轲. 输、配电网状态估计算法研究[D]. 合肥: 合肥工业大学, 2013.

REN Keke. Research on the algorithm of transmission and distribution state estimation[D]. Hefei: Hefei University of Technology, 2013.

(责任编辑 郭金光,王莹莹)

Method for closed loop current calculation based on CIM topological contraction

PEI Xingyu1, LIANG Zhipeng2, PENG Xiangang2, WENG Yishan1

(1. Zhuhai Power Supply Bureau of Guangdong Power Grid Corporation, Zhuhai 519000, China; 2. School of Automation, Guangdong University of Technology, Guangzhou 510006, China)

Aiming at the lack of timeliness for the offline study on closed loop current, this paper proposed a kind of on-line method for closed loop current calculation for distribution networks. It was a method that carried out real-time topology analysis of the higher grid, based on the data from CIM and SCADA, to achieve node merge and network contraction and got a ring network real-time calculation model. Based on the ring network real-time calculation model, at the meantime, it adopted the method of state estimation to solve the influence of real-time data measurement error on the calculation accuracy of closed loop bus voltage phase angle. The example analysis proves the accuracy and effectiveness, which provide theoretical evidence for the development of regional power grid on-line closed loop auxiliary decision system.

CIM model; switch information; state estimation; closed loop current

2015-09-17。

中国南方电网公司科技项目 (K-GD2014-0891)。

裴星宇(1982—),男,工程师,主要从事电力系统运行分析与控制研究工作。

TM727.2

A

2095-6843(2016)01-0006-05