基于吸引度搜索的汽车滚装码头堆场车位分配优化

陈 晓 静， 胡 志 华*， 李 功 君

( 1.上海海事大学 物流研究中心， 上海 201306；2.上海海通国际汽车码头有限公司， 上海 200137 )



基于吸引度搜索的汽车滚装码头堆场车位分配优化

陈 晓 静1， 胡 志 华*1， 李 功 君2

( 1.上海海事大学 物流研究中心， 上海 201306；2.上海海通国际汽车码头有限公司， 上海 200137 )

为加快滚装运输过程中汽车装卸滚装船舶的周转率，促进滚装码头堆场车位资源的高效利用，研究了滚装码头堆场车位分配问题．按照成组集中分配原则，以提高成组汽车停放集中度为目标，建立了衡量成组汽车停放集中度的混合整数规划模型．进而设计吸引度搜索算法对模型进行了求解．与分支定界法相比，吸引度搜索算法在高效求解规模化算例的同时可实现解的质量较优．以上海海通汽车滚装码头堆场的车位实际布局及作业情况为背景，验证了所提模型与算法的合理性及有效性，拓展了汽车滚装码头堆场车位分配管理的理论研究．

滚装码头堆场；车位分配；集中度；混合整数规划；吸引度搜索算法

0 引 言

汽车滚装码头堆场车位分配作业是影响滚装运输作业过程中汽车装卸船舶周转率及堆场车位资源利用率的关键环节．在实际滚装运输过程中，部分水道和港湾因受潮汐影响，使得滚装船舶必须在高潮前后才能航行和进出码头，这就对汽车装卸滚装船舶的时效性具有较高的要求．此外，随着汽车滚装码头年吞吐量的增长，加之汽车无法在堆场内堆垛存储的特性，使得堆场车位资源趋紧的现象也日益凸显．研究滚装码头堆场车位分配作业对加快汽车装卸过程的周转速度，提高堆场车位资源利用率具有重要意义．

滚装运输业务量的增长促使堆场车位分配作业的工作量加大，采用合理的算法可实现对数学模型规模化算例的高效求解．与集装箱作业相比，目前国内外关于汽车滚装作业的研究仍相对较少，且多数属于早期文献．Mattfeld等[1]参考不来梅港的汽车调度机制，针对库存控制及人力计划建立决策模型，并将其分层处理，设计启发式算法加以求解；Fischer等[2]详细描述了汽车转运港口的多Agent系统，探究了堆场车位的分配及调度计划，并通过算例设计对随机生成的汽车储位问题加以检验；Mattfeld等[3]提出了基于启发式算法的堆场容量利用策略来平衡计划期内堆场车位的分配，指出与遗传算法相比，启发式算法能够在较短的时间内找到更好的解决方案；Cordeau等[4]从管理层、战略层的角度出发，分析了汽车堆场中存在的管理问题，采用自适应大规模邻域搜索算法对所建立的数学模型加以求解．

本文针对滚装码头堆场车位分配问题，按照成组集中分配原则，以提高堆场内成组汽车停放集中度为目标，建立混合整数规划模型．设计吸引度搜索算法，分别采用分支定界法与吸引度搜索算法对多组实验场景进行求解，验证其合理性及有效性．

1 问题描述

滚装码头作为汽车供销渠道，为整车运输提供中转节点，能够对车辆流通过程中的时间和空间加以压缩，减少汽车物流中的阻碍[5]．其堆场作为汽车运输物流链中的重要节点，具有库存缓冲作用[6]，可吸收或缓解牛鞭效应，大幅度降低汽车物流成本，促进汽车物流利润实现最大化[7]．随着汽车滚装业务的发展，模块化布置方式的滚装码头堆场车位布局逐渐成为主流．图1给出了上海海通汽车滚装码头外四堆场的部分车位布局图，各模块的周边都设有通道，每个模块内的车位呈矩形集中布置．

经同一滚装船卸载的相同类型的汽车一般具备相同的出港时间要求，将其按型号划分成不同的组别，分别停放于一个辐射范围尽可能小，集中度尽可能大的停车区域内，可满足汽车堆存量及提取、停放便捷的双重要求，从而加快汽车装卸过程的周转速度，提高堆场车位资源利用率．基于此，按照成组集中分配原则，建立数学规划模型，在使同一组别的汽车在堆场内集中停放的基础上，达到各组汽车同时集中停放的效果，优化堆场车位分配作业．

目前已有的文献中尚未发现以成组集中分配为指标的堆场车位分配问题的研究．而在实际堆场操作作业中，堆场车位的分配也大都依赖于调度人员的实际操作经验．堆场车位分配问题实质上是将不同组别的车辆分配至堆场的各个车位，形成堆场车位分配计划．就模型建立方面，必然涉及以0-1变量来描述各个车辆在堆场中被分配的位置，从而形成混合整数规划模型．而在其他领域中大多数此类问题都具有NP-hard性质，因此，如何设计高效的算法对模型进行有效求解也是本文需要解决的难点．

图1 上海海通汽车滚装码头堆场部分车位布局图

2 模型建立

(1)集合说明

①{(r,c)}为每个停车位所对应的行列位置集合，r=1,2,…,R，c=1,2,…,C．

②A为待作业的汽车集合，由a∈A索引．

③G为相同型号的汽车组别集合，由g∈G索引．

(2)参数说明

①Bg,a：0-1参数，汽车a属于g组时取1，否则为0．

③R,C：分别表示汽车堆场的行数、列数．

④Xr,c∈G：堆场内第r行第c列的车位对应取值为已停放其内的汽车组别．

(3)变量说明

①xa,r,c：0-1变量，汽车a停放于堆场内第r行第c列的车位时取1，否则为0．

⑩yg,r1,r2,c1,c2：0-1变量，g组内所有汽车均被停放于堆场内由行[r1,r2]和列[c1,c2]所构成的区域时取1，否则为0．

图2给出了各变量间的逻辑关系．

图2 变量间逻辑关系

(4)衡量每组汽车集中度的函数描述

(1)

(2)

(3)

(5)成组集中策略下汽车滚装码头堆场车位分配模型

(4)

约束条件为

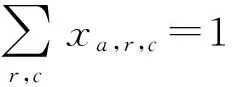
(5)

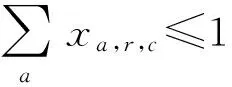
(6)

(7)

(8)

(9)

(10)

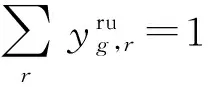
(11)

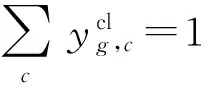
(12)

(13)

(14)

(15)

(16)

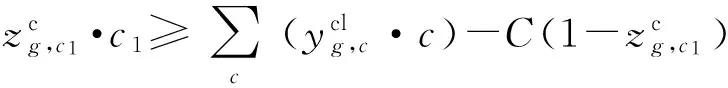
(17)

(18)

(19)

(20)

3 基于吸引度搜索的启发式算法设计

3.1 堆场车位分配特征分析

根据汽车滚装码头堆场车位布局特点，将堆场车位布置抽象为二维网络格局，如图3所示．每个格子代表一个车位，每个车位坐标可由具体的行列数(r,c)表示，并被赋予不同的状态．其中-1代表作业前初始堆场内已被占据的车位，不再参与分配作业；0代表作业结束后，堆场内未被分配的车位；其余数字则分别代表了待作业的各组汽车组别．根据本文模型中的目标函数，堆场车位分配的目标在于尽可能使同组内的汽车在堆场中集聚放置．因此，对于任何一个可行解，建立堆场车位分配吸引度的概念去表征同组汽车在堆场内存放的局部集聚水平，具体定义与计算方法可见3.2、3.3．同时，基于堆场中各位置的车位对不同组别汽车的吸引度，采用交换的策略以使得局部集聚水平不断得到提高．通过遍历搜索，最终使得堆场车位的分配布局达到次最优的状态．

3.2 吸引度定义

(1)符号说明

③ψ(r,c)：堆场内(r,c)位置车位的邻域空间．

④ψg,a：0-1参数，g组中第a辆汽车的车位属于ψ(r,c)时取1，否则为0．

⑤s：0-1参数，堆场内(r,c)位置的车位属于ψ(r,c)时取1，否则为0．

(2)吸引度水平

(21)

(22)

(3)总吸引度指标

(23)

图3给出了4行6列的堆场内(1,1)、(2,6)、(3,4)3个位置车位对各组汽车吸引度水平的计算示例．

3.3 算法步骤

Step 1 (初始化)将待作业汽车随机存放到堆场内未被占据的车位中，得到堆场车位分配方案P．

图4给出了4行6列的堆场内(3,4)位置车位依据吸引度水平对各组汽车进行搜索交换的示例．

图3 吸引度水平计算示例

Fig.3Calculatingdemonstrationsofattractiondegreelevel

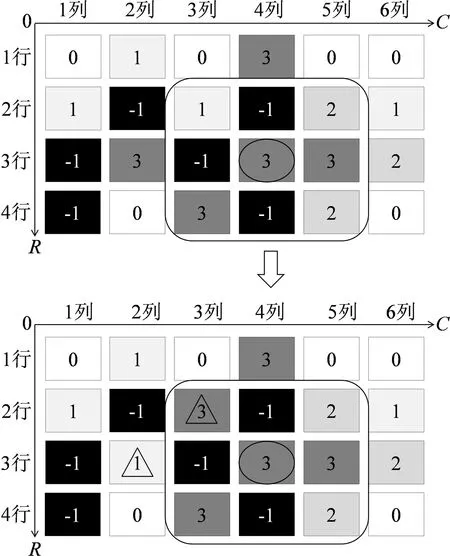
图4 基于吸引度水平的滚装码头堆场汽车搜索交换示例

Fig.4 A demonstration of vehicles search and swap in ro-ro yard based on attraction degree level

4 数值实验设计与分析

4.1 数值实验设计

4.2 实验结果分析

采用分支定界法与吸引度搜索算法求解上述数值实验，其中分支定界法通过CPLEX来实现．图5、6分别给出了采用吸引度搜索算法求解实验场景1算例3及实验场景3算例2所得到的滚装

表1 数值实验设计

图5 实验场景1算例3滚装码头堆场车位

Fig.5 Distribution scheme of parking space in ro-ro yard based on the third example in the first experiment scene

图6 实验场景3算例2滚装码头堆场车位

Fig.6 Distribution scheme of parking space in ro-ro yard based on the second example in the third experiment scene

码头堆场车位分配方案，与分支定界法计算结果(表2)作比，前者获得了最优解，误差为0，后者误差为0.03．从计算结果及计算时间来看，随着待作业汽车组数、待作业汽车总数的增加，以及堆场布局规模的扩大，吸引度搜索算法的计算时间远远小于分支定界法．且在堆场规模依次递增的实验场景3中，算例5、6计算时间长达72 h，分支定界法仍未得到最优解．实验结果证明了吸引度搜索算法在高效求解规模化算例的同时可实现解的质量较优．

5 实际应用

根据海通码头外四堆场布局及汽车分配作业的实际情况，仿照表1实验场景1设计应用算例(表3)．如图1中B4区所示，选取13行10列的堆场布局，通过调整已占车位坐标，控制已占车位率为0.3，已占车位分散度为0.5，运用吸引度搜索算法求解．从计算结果(图7)可以看出， 在每组实验中，随着待作业汽车组数的增加，f值逐渐增大，这与成组集中分配策略下滚装码头堆场车位分配模型表征意义相符．此外，待作业汽车组数的增加导致堆场内每个车位具备的吸引度水平种类增多，堆场内不同组别的汽车搜索交换过程变复杂，从而采用吸引度搜索算法求解所需要的CPU计算时间也依次递增(图8)．

表2 分支定界法与吸引度搜索算法结果对比

表3 实际应用算例设计

图7 计算结果统计

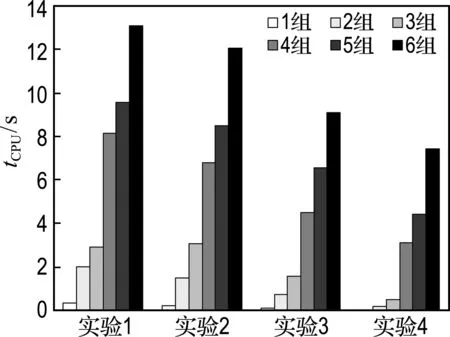
图8 计算时间统计

6 结 语

本文针对滚装码头堆场车位分配问题，按照成组集中分配原则，建立了衡量成组汽车停放集中度的混合整数规划模型，并设计吸引度搜索算法求解．与分支定界法对比的数值实验结果表明，吸引度搜索算法在解的质量上趋近于分支定界法，且运算时间远小于分支定界法，能够高效处理大规模算例．根据海通码头外四堆场的实际布局及作业情况设计算例，进一步分析了研究成果的应用情况．验证了堆场车位分配模型的合理性及吸引度搜索算法的有效性，拓展了汽车滚装码头堆场车位分配管理的理论研究，在优化车位分配的基础上促进了滚装运输作业的高效运行．

[1] Mattfeld D C, Kopfer H. Terminal operations management in vehicle transshipment [J]. Transportation Research Part A:Policy and Practice, 2003, 37(5):435-452.

[2] Fischer T, Gehring H. Planning vehicle transshipment in a seaport automobile terminal using a multi-agent system [J]. European Journal of Operational Research, 2005, 166(3):726-740.

[3] Mattfeld D C, Bierwirth C. An efficient genetic algorithm for job shop scheduling with tardiness objectives [J]. European Journal of Operational Research, 2004, 155(3):616-630.

[4] Cordeau J-F, Laporte G, Moccia L,etal. Optimizing yard assignment in an automotive transshipment terminal [J]. European Journal of Operational Research, 2011, 215(1):149-160.

[5] Dias J C Q, Calado J M F, Mendonca M C. The role of Europeanro-roport terminals in the automotive supply chain management [J]. Journal of Transport Geography, 2010, 18(1):116-124.

[6] Mendonca M C, Dias J C Q. ′Postponement′ in the logistical systems of new automobiles marketed in Portugal:the brands and quality [J]. Total Quality Management & Business Excellence, 2007, 18(6):681-696.

[7] Chen I J, Paulraj A. Understanding supply chain management:Critical research and a theoretical framework [J]. International Journal of Production Research, 2004, 42(1):131-163.

Optimization for parking space distribution in automotive ro-ro yard based on attraction degree search

CHEN Xiao-jing1, HU Zhi-hua*1, LI Gong-jun2

( 1.Logistics Research Center, Shanghai Maritime University, Shanghai 201306, China；2.Shanghai Haitong International Automotive Terminal Co., Ltd., Shanghai 200137, China )

In order to speed up the turnover ratio when automobiles roll up and roll down ro-ro ships in the process of ro-ro transportation and promote the utilization of parking space in ro-ro yard efficiently, the problem of parking space distribution in ro-ro yard is explored. According to the principle of centralized allocation of gathered groups,focusing on improving concentration degree of batch automobiles, a mixed-integer programming model is constructed to measure concentration degree of batch automobiles. Then attraction degree search algorithm is designed to solve the model. Compared with branch and bound method,the attraction degree search algorithm can deal with large-scale numerical examples efficiently and get satisfied solutions at the same time. Using the layout of parking space and operation conditions in Shanghai Haitong automotive ro-ro yard as research background, the proposed model and algorithm are proved to be reasonable and valid, which expand the theoretical research of parking space distribution management in automotive ro-ro yard.

ro-ro yard;parking space distribution;concentration degree;mixed-integer programming; attraction degree search algorithm

1000-8608(2016)02-0118-09

2015-09-03；

2016-01-12．

国家自然科学基金资助项目(71471109)；国家自然科学基金青年基金资助项目(71101088)；教育部博士点基金资助项目(20113121120002)；上海市教委科研创新项目(14YZ100)；交通部应用基础研究项目(2015329810260)；上海市曙光计划项目(13SG48).

陈晓静(1990-)，女，硕士生，E-mail:990598065@qq.com；胡志华*(1977-)，男，博士，教授，E-mail:zhhu@shmtu.edu.cn.

U651

A

10.7511/dllgxb201602002