分子动力学模拟高温高压下水的粘度

张钧惠，张欣，兰美华

（1.黑龙江八一农垦大学工程学院，大庆163319；2.大庆钻探工程公司钻井工程技术研究院；3.大庆钻探工程公司地质录井一公司）

将旋转矩阵和相关物理量分别由代换变量q1、q2、q3、q4表示。再结合刚体转动的欧拉方程，经过数学推导，可以得到加速度与四参数系统、角速度之间的相互关系如下：

分子动力学模拟高温高压下水的粘度

张钧惠1，张欣2，兰美华3

（1.黑龙江八一农垦大学工程学院，大庆163319；2.大庆钻探工程公司钻井工程技术研究院；3.大庆钻探工程公司地质录井一公司）

由于高温高压的极端条件实验室很难实现，因此应用分子动力学方法模拟计算水在高温高压下的粘度成为一种重要的手段。模拟实验基于分子动力学方法，针对水分子的特殊结构，引入Ewald法求长程作用力和四元素法，采用等温等压条件，最终模拟得到不同温度、压强下水的粘度并与实验值进行比较分析。

分子动力学；长程作用力；等温等压；四元素法；剪切应力；粘度

分子动力学模拟（molecular dynamics simulation，MD）以经典牛顿力学为理论基础，系统中各粒子的运动服从拉格朗日方程或哈密顿方程，通过粒子运动与轨迹的联系模拟系统中粒子的相关热力学性质。由于分子动力学模拟可以有效弥补理论分析和实验观察的不足，能够获得分子运动的各种微观特性，揭示各种现象的本质。因此，分子动力学模拟逐渐成为国内外学术界的研究热点，在材料科学、物理学、化学、生物学等领域得到广泛应用［1-5］，已逐步成为第三种科学研究手段。

水在农业、工业等各个领域都起着不可替代的作用［6］，水在各种极端条件下性质的研究迫在眉睫。然而超高温高压、超临界状态等极端条件在实验室很难甚至不能达到，因此水的分子动力学模拟便成为研究极端条件下水的相关性质的唯一方法。目前，针对极端条件下的分子动力学模拟研究日益增多，马静等［7］模拟了超（近）临界水溶剂特性，给出了水在常温、近临界和超临界状态的内聚能、溶解度参数与温度、压力的关系。孙炜等［8］模拟了温度为673.15～873.15 K，压力为22.1～131.3 MPa条件下水的密度和自扩散系数。然而，对高温高压下水的粘度的研究仍未进行，针对以上情况，推导了分子动力学模拟时长程作用力的计算公式和粘度计算公式，并分别模拟了温度为473.16 K、573.16 K，压强为10 MPa、20 MPa的高温高压条件下水的粘度。

1 模型建立及理论基础

1.1 初始条件、边界条件

采用各端自由的三维模型，系综为NPT系综。系统的初始位置采用面心立方排布，初始速度满足Maxwell-Boltzmann分布，周期性边界条件。

1.2 势函数

采用TIP4P型势函数［9］：

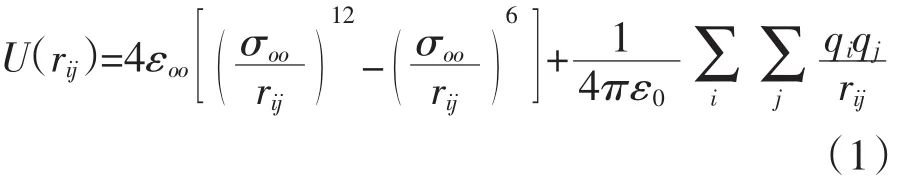
TIP4P型势函数参数为：εoo=1.077 2×10-21J，σoo= 0.315 4 nm，rOH=0.095 72 nm，rOH=0.015 nm，∠HOH= 104.52°，ε0=8.854×10-12C2·J-1·m-1，qH=0.52 e，qM= -1.04 e，e=1.602 19×10-19C。

1.3 分子间相互作用力

对势函数求导可得相邻水分子间的非键结力和静电力。由叠加原理可得水分子i在x方向所受合力为

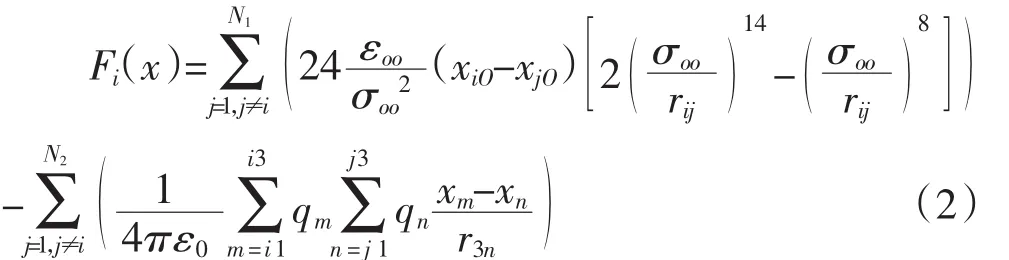
式中，第一项为非键结力，在模拟过程中只需考虑截断半径内的非键结力即可；第二项为静电力，由于静电力随半径收敛速度较慢，因此引入长程作用力，采用Ewald加和法来计算分子间的长程作用力。

考虑边长为L，含有N个水分子的立方体元胞盒子，则系统盒内的水分子以Ewald方法计算的系统电荷作用势的表达式为：

式中的势能分为三项为Ur、Uk、Us，其中，Ur为系统中水分子间的相互作用，n=L（nx，ny，nz），nx，ny，nz=0， ±1，±2…，erfc为余误差函数，α为控制收敛速度的经验参数，取α=5/L；Uk为系统中水分子与其他水分子的镜像水分子间的相互作用，其中k=2π（nx，ny，nz）/L，为保证模拟结果的准确性和提高模拟效率，取nx，ny，nz=0，±1，±2，±3。

分别对Ur、Uk、Us求导，可得水分子i在x方向所受的长程作用力Fix的表达式：

1.4 等温等压调节

在每个时间步，速度乘以速度标定因子，逐步调整系统温度达到恒定。速度标定因子的表达式为：

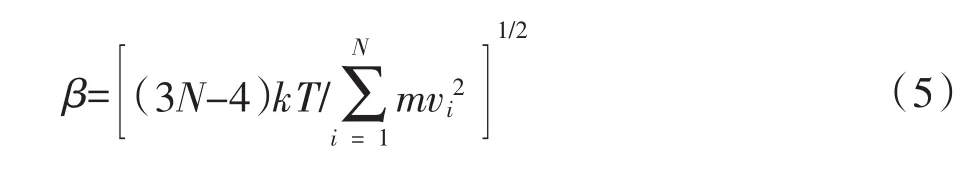
式中，β为速度标定因子；波尔兹曼常数k=1.38× 10-23J·K-1；T为温度；水分子质量m=2.987×10-23g。

采用Anderson方法对系统压力进行调整。在每个时间步，将水分子质心坐标乘以一个系数调整系统体积，进而达到调整系统压强的目的。

引入变量V后，系统的Lagrange方程调整为：

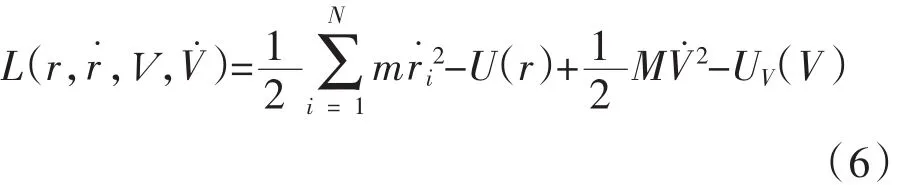
采用Velocity-Verlet算法［10］分别对S，V，s˙，V˙进行离散，可得等压调整的模拟计算公式：

1.5 四元素法

考虑水分子的平移运动和自身的旋转运动建立全局坐标系oxyz和原点在水分子质心上的局部坐标系o′x′y′z′。由理论力学可知，旋转变换矩阵中含有大量欧拉角的三角函数，而计算机计算三角函数非常耗机时，因此引入四个与欧拉角θ、φ、φ相关的变量q1、q2、q3、q4，

这四个变量q1、q2、q3、q4满足

将旋转矩阵和相关物理量分别由代换变量q1、q2、q3、q4表示。再结合刚体转动的欧拉方程，经过数学推导，可以得到加速度与四参数系统、角速度之间的相互关系如下：

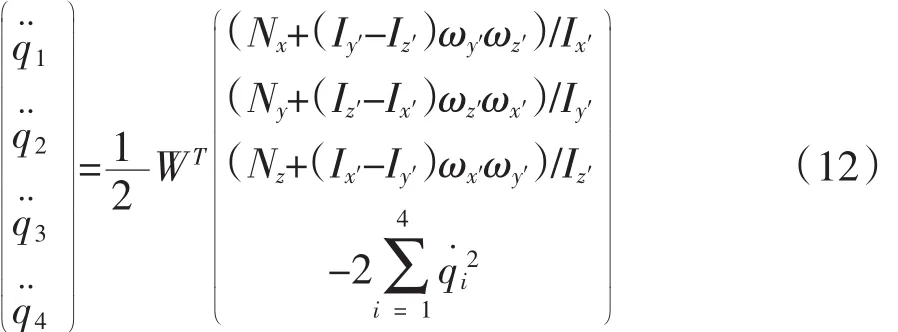
1.6 粘度计算

在模拟过程中，计算并记录系统的应力数据后，通过对时间取平均的方法求得物质的粘度，以下是粘度的计算公式：

式中，ηs为粘度为系统的应力分量，当α=β时，Pαβ为正应力；当α≠β时，Pαβ为剪切应力，〈Pαβ（0）Pαβ（t）〉表示应力的自相关函数。

把n组应力模拟数据平分为两组：Pαβ（1）、Pαβ（2）…Pαβ（n/2）和Pαβ（n/2+1）、Pαβ（n/2+2）…Pαβ（n）。令Qαβ（t）=〈Pαβ（0）Pαβ（t）〉，经过离散计算得到模拟计算的粘度公式：

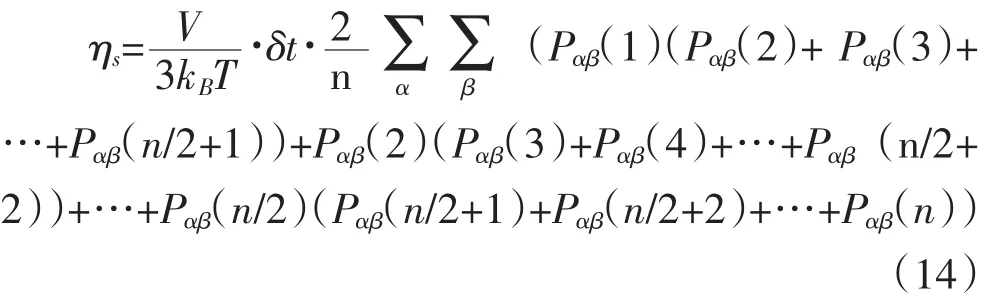
由于粘度是一个宏观统计量，需要进行足够时间的循环，记录大量的剪切应力值，才能得到比较准确的粘度值。

2 模型结果与分析

选取7×7×7的分子动力学模型，系统中含有1 688个水分子，取截断半径取为2.5σoo。实例分别模拟了温度为573.16 K、473.16 K，压强为10 MPa、20 MPa条件下水的粘度。模拟先经过10万步的弛豫过程，使分子动力学模拟系统达到平衡，再循环30万步统计平均正应力和平均剪切应力数据，并根据应力与粘度的关系计算水在不同温度和压强下的粘度。在对水的应力计算时，只统计距离各边界0.5α0以内区域的受力。

图1 平均正应力Fig.1Average normal stress

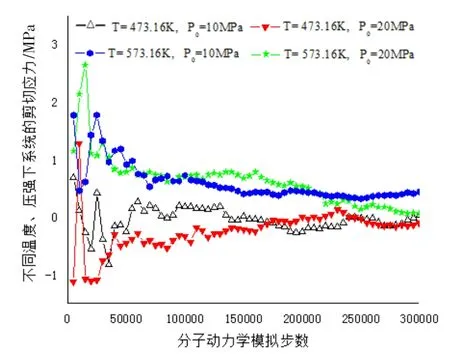
图2 平均剪切应力Fig.2Average shear stress

图1、2分别给出不同温度、压强下，系统平均正应力、平均剪切应力的变化情况。由图可得：在四种给定的温度、压强条件下，系统的平均正应力和平均剪切应力在模拟的初始阶段波动较大，随着模拟时间步的推移，波动逐渐变小，最终，平均正应力逐步趋向期望的压强值10 MPa和20 MPa，平均剪切应力在0 MPa附近上下波动。

图3给出不同温度、压强下水的模拟粘度的变化情况，图中图像表明：模拟的初始阶段水的模拟粘度值波动较大，随着模拟时间步的推移，水的模拟粘度值上、下波动越来越缓，逐步趋向稳定。

表1给出不同的温度、压力下水的粘度模拟值及其与化学化工物性数据手册［11］中的试验值的比较分析。

图3 水的粘度Fig.3Viscosity of water

表1 不同温度、压强下系统的剪切粘度Table 1Viscosity under different temperatures and pressure

综合观察图3和表1可得，当模拟系统的温度保持不变时，压强增大则水的模拟粘度值增大；当模拟系统的压强保持不变时，温度升高则水的模拟粘度值减小。这与化学化工物性数据手册中的粘度的变化规律一致。

3 结论

基于分子动力学模拟理论，针对水分子特殊的极性分子结构，引入Ewald加和法计算长程作用力，为避免水分子平移和旋转运动相关的大量三角函数的计算，引入四元素法。模拟通过温度压力调整达到等温等压，最终根据粘度的模拟计算公式，由剪切应力的统计数据求得在高温高压下水的粘度值。取7× 7×7的模拟系统，系统温度、压强分别为：473.16、573.16 K，10、20 MPa时，水的模拟粘度值与实验粘度数据的相对误差分别在1.88%～6.97%之间，且水的模拟粘度随着温度的升高而减小，随着压强的增大而增大，与实验所得粘度的变化规律一致。

［1］徐尧，刘跃龙，刘够生.水分子在白云母表面吸附的分子动力学模拟［J］.化工学报，2014（12）：4814-4822.

［2］Song H L.The Rheology of Liquid Pentane Isomers by Non-Equilibrium Molecular Dynamics Simulations［J］. Molecular Simulation，2000，23（4）：243-256.

［3］李健，杨延清，罗贤，等.分子动力学模拟在复合材料界面研究中的进展［J］.稀有金属材料与工程，2013，42（3）：644-648.

［4］Wei L，Yang C L，Zhu Y T，et al.Interactions Between Single-Walled Carbon Nanotubes and Polyethylene/Polypropylene/Polystyrene/Poly（phenylacetylene）/Poly（p-phenylenevinylene）Considering Repeat UnitArrangements and Conformations：A Molecular Dynamics Simulation Study［J］.The Journal of Chemical Physics，2008，112：1803-1811.

［5］Susumu Kotake.Molecular Simulation Engineering［J］. JSME International Journal，1995（1）：38-48.

［6］黄富才，吕艳东，郭晓红，等.结实期水分供应对寒地水稻灌浆动态和产量的影响［J］.黑龙江八一农垦大学学报，2013，25（1）：12-18.

［7］马静，董秀芹，张敏华.超（近）临界水溶剂特性的分子动力学模拟［J］.计算机与应用化学，2007，24（7）：872-874.

［8］孙炜，黄素逸，王存文，等.超临界水密度和自扩散系数预测的分子动力学模拟［J］.华中科技大学学报：自然科学版，2008，36（5）：103-105.［9］Chen C K，Lin D T.TIP4P Potential For Lid-Driven Cavity Flow［J］.Acta Mechanica，2004（178）：223-237.

［10］Swope W C，Anderson H C.Computer Simulation Method for the Calculation of Equilibrium Constants for the Formation of Physical Clusters of Molecules：Application to Small Water Clusters［J］.The Journal of Chemical Physics，1982（76）：637-649.

［11］刘光启.化学化工物性数据手册（无机卷）［M］.北京：化学工业出版社，2002.

Water Viscosity of Molecular Dynamics Calculations under Different Temperatures and Pressure

Zhang Junhui1，Zhang Xin2，Lan Meihua3
（1.College of Engineering，Heilongjiang Bayi Agricultural University，Daqing 163319；2.Daqing Oilfield Drilling Engineering and Technology Institute；3.No.1 Logging Company，Daqing Drilling and Exploration Engineering Corporation）

It is difficult to achieve in the lab under the extreme conditions of high temperature and high pressure，therefore，it is an important method to calculate the water viscosity in high temperature and high pressure by using molecular dynamics simulation. Based on molecular dynamics simulation and special structure of water molecules，this paper introduced Ewald method for long-range force and four-element method.Finally，the viscosity under different temperature and pressure was simulated in the isothermal isobaric system，and the results were compared with the experimental value.

molecular dynamics；long-range force；isothermal pressure control；four-element method；shear stress；viscosity

O313

A

1002-2090（2016）04-0089-04

10.3969/j.issn.1002-2090.2016.04.020

2015-06-06

张钧惠（1981-），女，助教，燕山大学毕业，现主要从事力学方向的教学与研究工作。