HIGHT算法的积分攻击
郭建胜,崔竞一,潘志舒,刘翼鹏
(1. 解放军信息工程大学三院,河南 郑州 450001;2. 信息保障技术重点实验室,北京 100072;3. 西安卫星测控中心,陕西 西安 710043)
HIGHT算法的积分攻击
郭建胜1,2,崔竞一1,潘志舒3,刘翼鹏1
(1. 解放军信息工程大学三院,河南 郑州 450001;2. 信息保障技术重点实验室,北京 100072;3. 西安卫星测控中心,陕西 西安 710043)
对轻量级分组密码算法 HIGHT在积分攻击方法下的安全性进行了研究。首先纠正了现有研究成果在构造区分器时的不当之处,重新构造了HIGHT算法的11轮积分区分器,并构造了相应高阶积分扩展下的17轮区分器;其次利用所构造的17轮区分器,结合“时空折中”原理对25轮HIGHT算法进行了积分攻击;最后对攻击算法的复杂度进行了分析,攻击算法需要的数据复杂度为262.92,时间复杂度为266.20,空间复杂度为2119。分析结果表明,所给出的攻击算法的攻击轮数和时间复杂度要优于现有研究结果。
密码分析;分组密码;积分攻击;HIGHT算法
1 引言
HIGHT算法是由Hong等[1]在CHES 2006上提出的轻量级分组密码,其采用一种广义Feistel结构,轮函数输入和输出均为8 bit,规模很小,且没有用S盒,只使用循环移位、异或和模加操作,在8位处理器的环境中表现出很好的效率。子密钥是在加密过程中通过密钥扩展算法得到的,密钥寄存器只需要存储128 bit的主密钥。
针对 HIGHT的分析方面,最初由设计者给出了 HIGHT算法的差分分析、线性分析、截段差分分析、不可能差分分析、积分分析等结果[1]。其积分分析构造了 12轮的积分区分器,并对 16轮HIGHT算法进行了攻击。2009年,文献[2]指出了算法设计者在构造积分区分器时的错误,利用高阶积分扩展构造了 17轮的积分区分器,并利用密钥扩展算法攻击了22轮HIGHT算法。在ICISC 2010上,Koo等[3]在相关密钥条件下给出了全轮HIGHT算法的攻击结果。在单密钥条件下,Hong等[4]在ICISC 2011上利用Biclique攻击给出了全轮HIGHT算法的攻击结果,但其时间复杂度较高。Chen等[5]在2012年非洲密码年会上提出了HIGHT算法不可能差分分析的相关结论。在 2015年,由 Igarashi等[6]提出了对19轮HIGHT算法的中间相遇攻击结果。同时,HIGHT算法也有在故障分析下安全性的相关研究成果[7,8]。
本文对 HIGHT算法在积分攻击下的安全性进行了研究。首先,对文献[2]所构造的积分区分器进行了分析,指出了文献[2]在构造区分器时的不当之处,重新构造了HIGHT算法的11轮积分区分器,并构造了相应高阶积分扩展下的 17轮区分器;然后,根据高阶积分扩展构造的 17轮区分器,攻击了25轮HIGHT算法。其中,根据“时空折中”的原理,利用存储空间分担了部分计算时间,降低了整个攻击算法的计算复杂度。攻击25轮HIGHT算法的数据复杂度、时间复杂度和空间复杂度分别为262.92、266.20和2119。攻击轮数和时间复杂度都要优于文献[2]与文献[11]的结果。
2 相关知识
2.1 HIGHT算法结构简介
HIGHT算法采用了具有8分支的广义 Feistel结构。其分组长度为64 bit,密钥长度为128 bit,加密轮数为32轮。每一轮包含2个不同的F函数(F :{0,1}8→{0,1}8, F :{0,1}8→ {0,1}8)、异或
0
1运算⊕、模28加运算以及内部位置变换。其F函数为: F0( x) =x <<<1 ⊕ x <<<2 ⊕ x<<<7,F1( x) = x <<< 3 ⊕ x <<< 4 ⊕ x<<< 6。设64 bit明文为经过32轮算法后变换成64 bit密文具体结构如图1所示。
HIGHT算法具体加密流程如下。
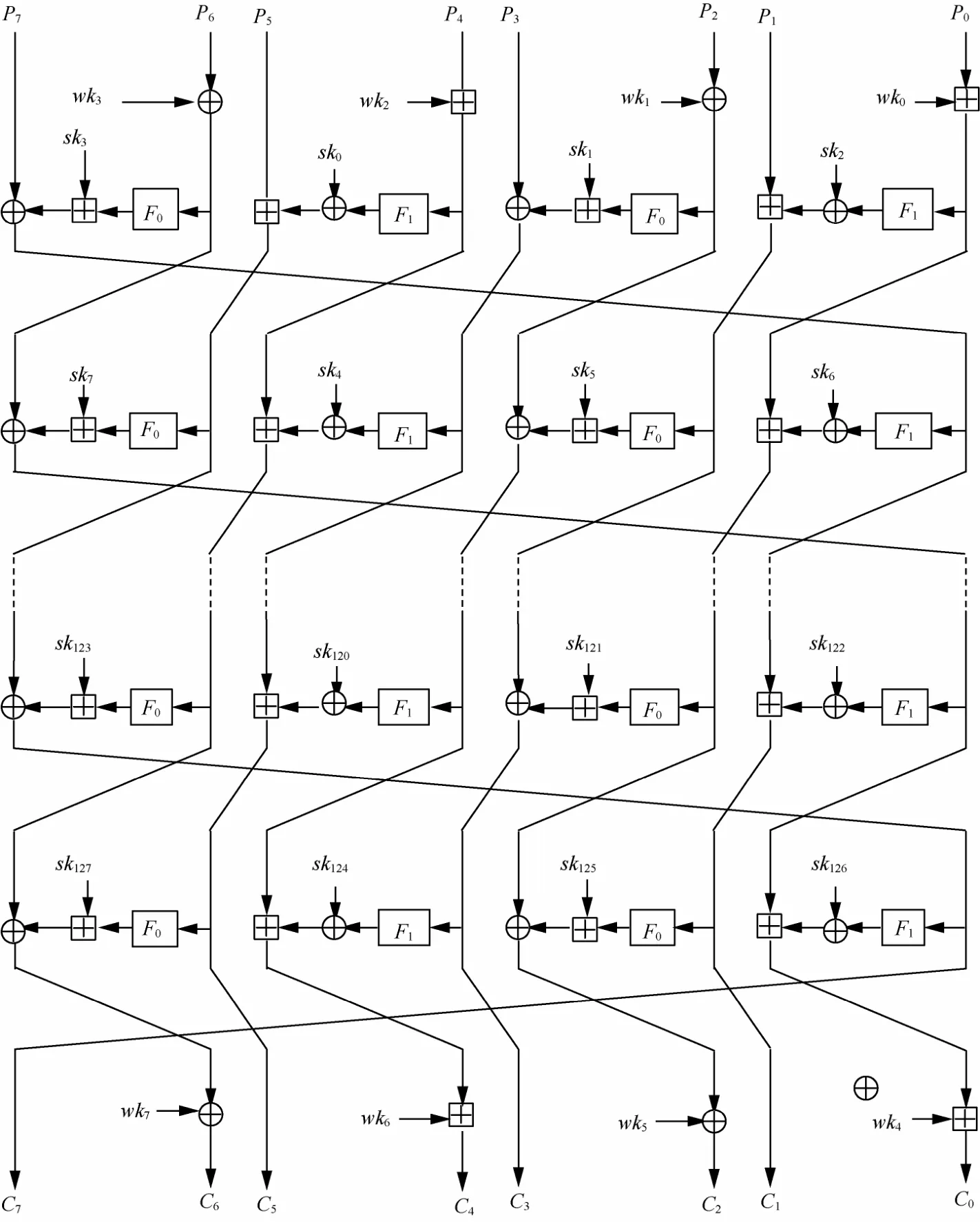
图1 HIGHT算法加密流程
1) 初始白化密钥加变换
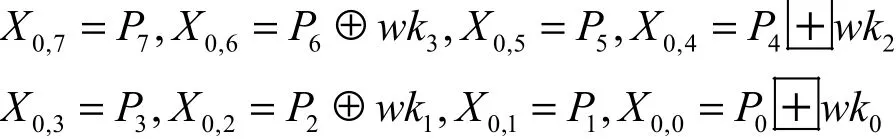
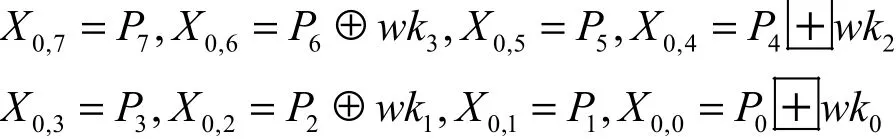
2) 轮变换
(Xi−1,7,Xi−1,6,Xi−1,5,Xi−1,4,Xi−1,3,Xi−1,2,Xi−1,1,Xi−1,0)为第i轮的输入,其中, i= 1,2,… ,31,则输出为
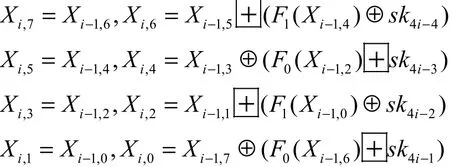
(X31,7,X31,6,X31,5,X31,4,X31,3,X31,2,X31,1,X31,0)为第32轮的输入,则对应的输出为
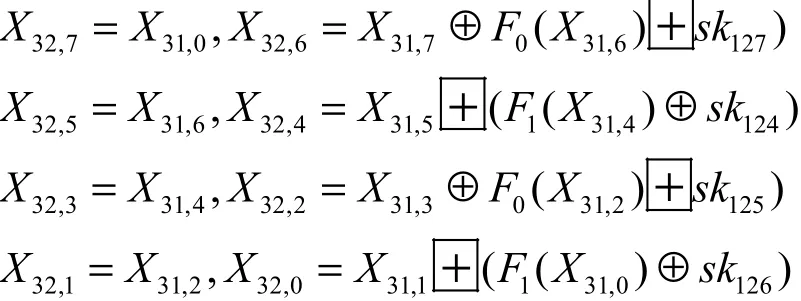
3) 结尾白化密钥加变换
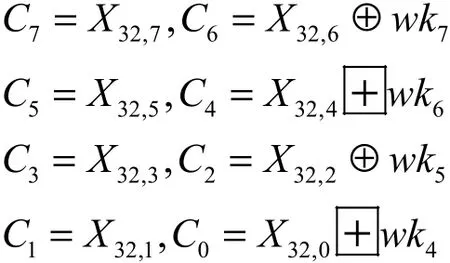
HIGHT算法的密钥扩展算法由两部分组成。第一部分是常数生成部分,利用线性反馈移位寄存器生成128个7 bit常数δ0,δ1… ,δ127;第二部分为白化密钥和子密钥生成部分,通过主密钥MK与第一部分生成的常数生成白化密钥和子密钥。首先将主密钥MK化分为16 byte,即 MK =(M K15,M K14,… ,M K0)。
白化密钥生成部分: wki= MKi+12(i = 0,1,2,3),wki= MKi−4(i = 4,5,6,7)。
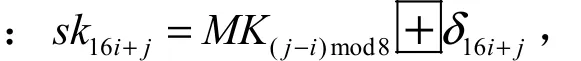
2.2 积分攻击
积分攻击是Knudsen等[9]总结提出的一种分组密码选择明文攻击方法,自提出以来,其得到了越来越广泛的关注,该攻击方法被应用于许多算法的安全性分析中,例如 AES[10]、LBlock[11]、E2[12]和MIBS[13]等。
积分攻击就是选择特定形式的明文进行加密,再对所得密文求和(积分),通过积分值的不随机性将密码算法与随机置换区分开。在构造积分区分器时,需要定义一些符号。
定义1[9,14]一些特殊形式的集合
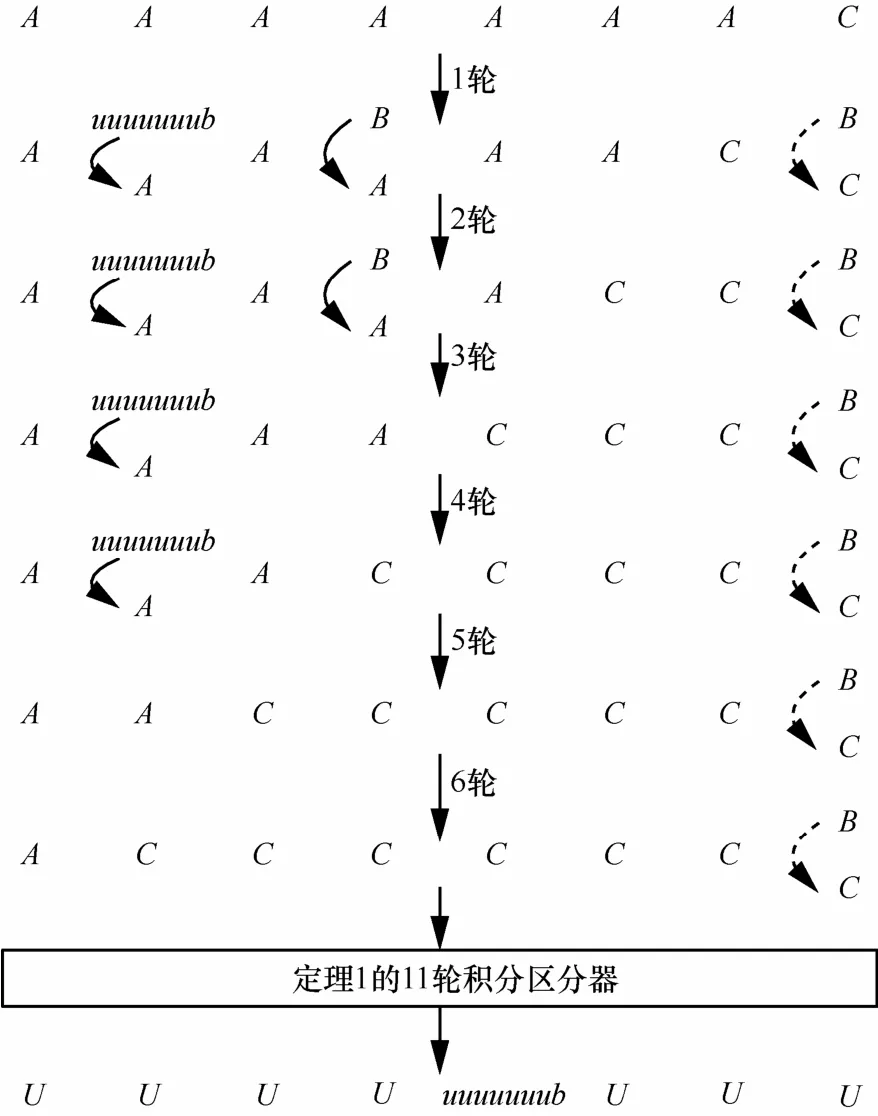
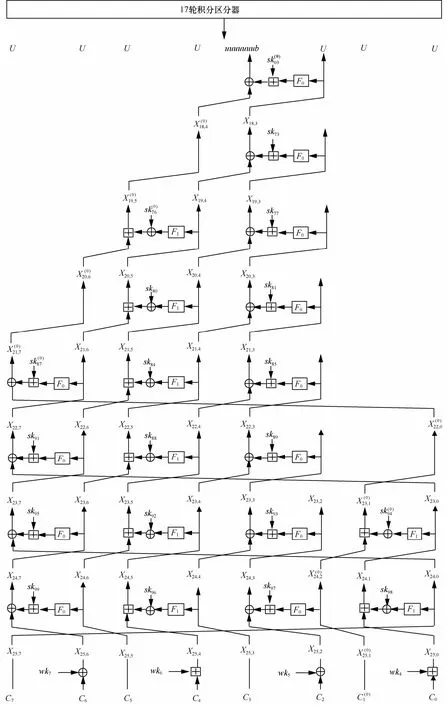
1) 活跃集:若对任意的0 ≤ i iji i2n集,记为A。 2) 稳定集:若对任意的0 i 0i i2n记为C。 0 ≤ i≤ 2n−1}是平衡集,记为B。 此外,记不能确定是否平衡的集合为U。这些集合之间的运算遵循一些基本原则。性质1[9,14]不同集合之间满足如下性质。1) 集合 A通过双射(如密钥加)后,仍是集合A;集合C通过双射后,仍是集合C。 2) 2个集合A的异或和不一定为集合A,但一定是集合B;集合A与集合C的异或和仍是集合A;2个集合B的异或和仍为集合B。 3) 集合B通过非线性双射(如模28加),将无法确定其平衡性。 本文讨论的 HIGHT算法以字节为操作单位,即将定义1中的n取8。 由于HIGHT算法涉及到模28加运算,有必要对不同形式集合间的模28加运算原则进行归纳,由性质1的3)进一步得到性质2。 性质2 不同集合类型的字节之间进行模28加运算遵循以下性质。 1)集合A与集合C的模28加和仍是集合A;集合B与集合C的模28加和仍是集合B。 2)集合B与集合A的模28加和无法确定其平衡性,但其最低比特仍保持平衡,记为 uuuuuuub;2个B集合的模28加和无法确定其平衡性,但其最低比特仍保持平衡,记为uuuuuuub。 证明 2个集合间的模28加运算结果:最低比特为2个集合最低比特之间进行异或加运算所得,其余比特为2个集合对应比特之间进行异或加运算再加上低比特的进位所得。由于集合B与集合A最低比特均为平衡比特,所以根据性质1的2) 可得,集合B与集合A进行模28加运算后,最低比特仍保持平衡,其余比特由于涉及到低比特的进位,平衡性不能确定。同理可得2个集合B的模28加运算的结果。 证毕 文献[2]给出了 HIGHT算法的 11轮积分区分器,在构造过程中,认为集合A经过F函数仍为集合A,根据性质1的2)可知,集合A经过F函数后应为集合B,据此,本文重新构造HIGHT算法的11轮积分区分器(定理1),所得结果与文献[2]仍相同。如图2所示。 定理1 (11轮积分区分器) 选择28个明文,满足条件:7P遍历所有 28个取值,即为集合均为固定值,即为集合C。则经过11轮HIGHT算法后,则输出的X11,3最低比特仍保持平衡。 图2 HIGHT算法的11轮积分区分器 进一步,文献[2]将 11轮区分器向前做高阶积分扩展,得到17轮积分区分器(定理2)。如图3所示。 定理2 (17轮积分区分器)选择256个明文,满足条件: P7, P6, P5, P4, P3,P2, P1分别遍历所有 28个取值,P0为固定值,即为集合C。则经过17轮HIGHT后,输出的X17,3最低比特仍保持平衡。 图3 17轮积分区分器 文献[2]在17轮积分区分器的基础上攻击了22轮 HIGHT算法,本文利用“时空折中”的原理降低攻击的计算复杂度,实现对25轮HIGHT算法的积分攻击。选取构造 17轮区分器时需要的明文,得到25轮加密的密文,通过猜测相关密钥,从25轮加密的结果恢复出第 17轮的结果,验证其中X17,3的最低比特是否平衡。 记字节X的最低比特为(0)X 。根据算法加密流程,攻击算法如下。 算法1 25轮HIGHT算法积分攻击 步骤1 选择构造17轮积分区分器时的明文(256个),进行25轮加密得到256个密文。 步骤2 猜测结尾密钥 wk7,w k6, w k5, wk4,对256个密文解密,计算第 25轮的输出: X25,7=C7, 步骤3 猜测第25轮子密钥 sk99,s k96,s k97,sk98,用步骤2的结果解密第25轮,得到256个第24轮部分输出步骤 4 猜测第 24轮子密钥 sk95,s k92,sk93和sk(0),用步骤3的结果解密第24轮,得到256个第 94 步骤5 猜测第23轮子密钥 sk91,s k88,sk89,用步骤4的结果解密第23轮,得到256个第22轮部分输出 步骤6 猜测第22轮子密钥 sk84, sk85, sk8(7 0),用步骤5的结果解密第22轮,得到256个第21轮部 分输 出其中, F0( X22,7)(0)表示 F0( X22,7)的最低比特。 步骤7 猜测第21轮子密钥 sk80, sk81,用步骤6的结果解密第21轮,得到256个第20轮部分输出: 步骤8 猜测第20轮子密钥sk77, sk7(60),用步骤7的结果解密第20轮,得到256个第19轮部分输出:表示 F1( X20,5)的最低比特。 步骤9 猜测第19轮子密钥sk73,用步骤8的结果解密第19轮,得到256个第18轮部分输出: (70,)3是否为平衡比特,若是,则所猜测的密钥为候选密钥,否则为错误密钥,删除。 步骤11 选择另一组构造17轮区分器时的明文,重复步骤1~步骤10,直至密钥唯一确定。 攻击流程如图4所示。 对算法1进行分析,利用存储空间分担算法的计算时间:单独计算算法中每一步骤的时间复杂度,存储每一步的计算结果,在下一步计算中调用上一步存储的结果,最后将每一步的时间复杂度相加得到整个算法的时间复杂度。得到定理3。 定理3 利用算法1对25轮HIGHT算法进行积分攻击,攻击的数据复杂度为262.92,时间复杂度为266.20,空间复杂度为2119。 证明 算法 1需要猜测 8 bit密钥 wk7, wk6,wk5, w k4,s k73,s k77,s k80,s k81,s k84,s k85,s k88,sk89,sk91,sk92,s k93,s k95,s k96,s k97,s k98,sk99和1 bit密钥 sk6(90),sk(0),s k(0),sk(0)。根据密钥扩展算法,这些密钥由某 76 87 94些主密钥生成,如表1所示。 根据算法1及表1可知,攻击过程中需要先后 猜 测 wk7, w k6, w k5, wk4; sk99, sk98; sk95,sk92,sk, sk(0);sk ,s k ,sk ;sk;sk的前 7 bit,sk, 9394918889847773共120 bit密钥。对于正确密钥,一定能保证为平衡比特;对于错误密钥,其使平衡的概率为,所以经过一组明密文淘汰后,剩余错误密钥数目为为了唯一确定正确密钥,需要121组明文,从而攻击的数据复杂度为121组( 256× 121 ≈ 262.92个明文)。 图4 25轮HIGHT算法的积分攻击 攻击的时间复杂度按如下方法估计:对第一组明文,步骤1需要256次25轮加密,步骤2需要猜测 wk7, w k6, w k5, wk4共32 bit密钥,共232个可能值,在密钥固定的情况下,结尾密钥模28加运算只依赖于C4和C0,取值最多216种(相同的不重复计算),最多需 232× 216× 2 = 249次模28加运算,步骤3需要猜测 sk99, sk98共16 bit密钥,216个可能值,在密钥固定的情况下,模28加运算依赖于 F0( X25,5),X24,4,共48 bit,最多248个可能值,最多需 216× 248× 4 = 266次模28加运算,步骤4需要猜测 sk95,s k92,s k93,sk9(40)共25 bit密钥,共225个可能值,在密钥固定的情况下,模28加运算依赖于共32 bit,最多232个可能值,最多需要 225× 232×3 = 258.58次模28加运算,同理,步骤 5需要猜测 sk91s k88,sk89共24 bit密钥,最多需要 224× 232× 3 = 257.58次模28加运算,步骤 6需要猜测sk84这 8 bit密钥,最多需28× 224× 2 = 233次模28加运算,步骤7需要猜测0 bit密钥,最多需 224×2=225次模28加运算,步骤8需要猜测sk77的前7 bit密钥,最多需 27×28=215次模28加运算,步骤9需要猜测sk73这8 bit密钥,最多需 28×28=216次模28加运算,步骤10计算量可忽略不计,由于25轮算法一共有4× 25 + 4 =104次模28加运算,因此,在忽略其他运算所耗时间的情况下,模28加运算转换为25轮加密操作,相当于次25轮加密;处理完第一组明文后,错误密钥还剩2119个(大于232),同理处理第二组明文最多需259.45次 25轮加密;只要候选密钥剩余个数不小于232,处理每组明文均最多需259.45次25轮加密,因此当处理完89组明文后,剩余候选密钥231个,处理第90组最多需次25轮加密;处理完90组明文后,剩余候选密钥230个,处理第91组最多仍需259.45次25轮加密;类似地,处理后30组明文分别最多需 259.45, 259.45,259.45, 259.45, 259.45, 259.45, 259.44, 259.44, 259.44,259.44, 259.44, 259.44, 259.44, 258.57, 257.79, 257.16,256.69, 256.39, 256.21, 256.17, 256.05, 256.03, 256.01,256.01, 256, 256, 256, 256, 256次25轮加密。所以攻击过程时间复杂度不超过 259.45× 97 + 259.44×8+ 258.57+257.79+ 257.16+ 256.69+ 256.39+ 256.21+ 256.17+ 256.05+ 256.03+256.01× 2 + 256× 5 ≈ 266.20。此外,攻击过程中还需要2119的存储空间存储候选密钥,模28加运算的表以及攻击过程中每一步骤的某些中间数据。 表1 算法1所猜密钥与主密钥的关系 证毕 同理,可利用区分器I对25轮HIGHT算法进行攻击。 本文对HIGHT算法在积分攻击下的安全性进行了研究,纠正了文献[2]中构造 11轮区分器时的错误,通过向前做高阶积分将 11轮区分器扩展至17轮。依据17轮区分器,利用“时空折中”的原理降低计算复杂度,攻击了25轮HIGHT算法。攻击算法的数据复杂度、时间复杂度和空间复杂度分别为262.92、266.20和2119。攻击轮数和时间复杂度都要优于文献[2]的结果。 本文结果表明,针对广义 Feistel结构的算法,在拥有足够的存储空间的情况下,可以利用“时空折中”的原理攻击更多轮算法结构。在未来的工作中,将利用这一原理,对其他结构分组密码算法(SPN结构、Feistel结构等)进行分析,以达到在降低时间复杂度的同时,攻击更多轮算法的研究目的,进一步推广积分攻击算法的应用范围。 表2将本文积分攻击的结果与文献[2]的结果做了比较。 表2 HIGHT算法积分攻击的结果比较 [1] HONG D, SUNG J, HONG S, et al. HIGHT: a new block cipher suitable for low-resource device[C]//Cryptographic Hardware and Embedded Systems - CHES 2006. c2006: 46-59. [2] ZHANG P, SUN B, LI C. Saturation attack on the block cipher HIGHT[C]//The 8th International Conference on Cryptology and Network Security. c2009:76-86. [3] KOO B, HONG D, KWON D. Related-key attack on the full HIGHT[C]//Information Security and Cryptology - ICISC 2010. c2010:49-67. [4] HONG D, KOO B, KWON D. Biclique attack on the full HIGHT[C]//Information Security and Cryptology - ICISC 2011. c2011: 365-374. [5] CHEN J, WANG M, PRENEEL B. Impossible differential cryptanalysis of the lightweight block ciphers TEA, XTEA and HIGHT[C]// AFRICACRYPT 2012. c2012: 117-137. [6] IGARASHI Y, SUEYOSHI R, KANEKO T, et al. Meet-in-the-middle attack with splice-and-cut technique on the 19-round variant of block cipher HIGHT[J]. Infromation Science and Applications, 2015, 339: 423-429. [7] 范伟杰, 吴文玲, 张蕾. HIGHT算法的差分故障攻击[J]. 中国科学院研究生院学报, 2012, 29(2): 271-276.FAN W J, WU W L, ZHANG L. Differential fault analysis on HIGHT[J]. Journal of Graduate University of Chinese Academy of Science. 2012, 29(2): 271-276. [8] 陈浩, 王韬, 张帆, 等. HIGHT密码代数故障分析[J]. 上海交通大学学报. 2015, 49(12): 1817-1825.CHEN H, WANG T, ZHANG F, et al. Algebraic fault analysis of HIGHT[J]. Journal of Shanghai Jiaotong University, 2015, 49(12):1817-1825. [9] KNUDSEN L, WAGNER D. Integral cryptanalysis[C]//FSE 2002.Leuven, Belgium, c2002: 112-127. [10] MINER M, PHAN R W, POUSSE B. On integral distinguishers of rijndael family of ciphers[J]. Cryptologia, 2012, 36(2): 104-118. [11] YU S, LEI W. Meet-in-the-middle technique for integral attacks against feistel ciphers[C]//Selected Areas in Cryptography 2012. c2012: 234-251. [12] YI W, CHEN S. Integral cryptanalysis of the block cipher E2[EB/OL].http://arxiv.org/pdf/1404.6100.pdf. [13] YI W, CHEN S. Improved results on integral and zero-correlation linear cryptanalysis of the block cipher MIBS[EB/OL]. http://arxiv.org/pdf/1404.6100.pdf. [14] 李超, 孙兵, 李瑞林. 分组密码的攻击方法与实例分析[M]. 北京:北京科学出版社, 2010: 175-207.LI C, SUN B, LI R L. Block cipher attack method and example analysis[M]. Beijing: Beijing Science Press, 2010:175-207. Integral attack on HIGHT block cipher GUO Jian-sheng1,2, CUI Jing-yi1, PAN Zhi-shu3, LIU Yi-peng1 The security of HIGHT block cipher under integral attack was studied. Firstly, the flaw in the existing results on building the distinguisher was corrected. And a new 11-round integral distinguisher of HIGHT was built. Based on this new distinguisher, a 17-round multiple-integral distinguisher was built. By using the 17-round distinguisher, 25-round integral attack on HIGHT was proposed based on the principle of time memory trade-off, with the data, time and memory complexity of 262.92, 266.20and 2119respectively. The results show that the attack was better than results before on the number of round and time complexity. cryptanalysis, bock cipher, integral attack, HIGHT block cipher China Postdoctoral Science Foundation (No.2014M562582) TN918.1 A 10.11959/j.issn.1000-436x.2016135 2015-01-27; 2016-06-04 中国博士后科学基金资助项目(No.2014M562582) 郭建胜(1972-),男,河南沁阳人,解放军信息工程大学教授,主要研究方向为信息安全与密码学。 崔竞一(1992-),男,河南登封人,解放军信息工程大学硕士生,主要研究方向为分组密码设计与分析。 潘志舒(1985-),男,江苏镇江人,西安卫星测控中心助理工程师,主要研究方向为分组密码设计与分析。 刘翼鹏(1992-),男,山东烟台人,解放军信息工程大学硕士生,主要研究方向为信息安全与量子密码。3 HIGHT算法17轮积分区分器的构造

4 对25轮HIGHT算法的积分攻击
4.1 积分攻击流程
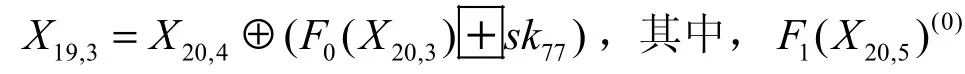
4.2 积分攻击算法的分析

5 结束语

(1. The Third Department, The PLA Information Engineering University, Zhengzhou 450001, China;2. Science and Technology on Information Assurance Laboratory, Beijing 100072, China;3. Xi’an Satellite Control Center, Xi’an 710043, China)




