一种基于稀疏自编码网络的数据降维方法研究
朱啸天,张艳珠,王凡迪
(沈阳理工大学 信息科学与工程学院,沈阳 110159)
一种基于稀疏自编码网络的数据降维方法研究
朱啸天,张艳珠,王凡迪
(沈阳理工大学 信息科学与工程学院,沈阳 110159)
高维数据的“维数灾难”问题制约了机器学习、模式识别等诸多研究领域的发展研究。因此高维数据的降维方法,即将高维的特征数据化简投射到低维空间中,成为当前研究热点之一。稀疏自动编码器(Sparse Autoencoder)网络通过训练具有多隐含层的神经网络将高维数据进行降维,能有效地解决了高维数据由于维数过大导致的识别率低的问题。将网络用于手写体数字图像识别及人脸图像识别实验,取得了较好地识别结果,表明稀疏自动编码网络能有效地对高维数据降维。
高维数据降维 ;稀疏编码;图像识别
近年来,随着科学技术的发展,在实际应用中经常会碰到高维数据,但由于“维数灾难”的影响,使得高维数据在机器学习及识别分类领域变得异常困难。传统方法是采用一些特殊的手段进行处理,而最常见的处理方式之一就是降维。通过数据降维可以减轻维数灾难以及高维数据中相关性较弱的冗余特征,从而促进高维数据的分类、压缩以及可视化。
目前已提出的许多降维方法[1-2],主要可分为线性和非线性两类, 线性降维方法主要有主成分分析(PCA)和线性判别分析(LDA)等。它们在具有线性结构以及高斯分布的高维数据集上具有好的降维效果。然而当高维数据呈现复杂以及非线性结构时,这些方法则难以发现能够表现数据集的主要特征[3],从而无法对其进行有效降维[4]。而根据先前的研究表明,大多数情况特征数据是分布在弯曲的流形空间中,因此流形学习方法即非线性降维方法如等度规映射(ISOMAP)[5]和局部线性嵌入算法(LLE)[4]等得到了广泛的应用。流形学习通常认为数据集具有能表达数据本质的维数,然后可以通过将数据集降维至低维空间来避免维数灾难问题,并发现隐含在数据中的内在物理意义。然而,现有大多流形学习方法[6-7]也存在缺陷。例如ISOMAP具有拓扑不稳定性而且短环路会严重影响它的执行;而LLE要求所学习的数据流行空间不能闭合而且局部要求线性,并且对噪声敏感。因此,采用这类降维方法必须联合运用其他复杂的技术来改进这些缺陷。
本文引入一种新的非线性降维方法——稀疏编码网络方法。该网络在自编码网络的基础上加入约束条件,使自编码网络每次得到的表达数据尽量稀疏,即通过少量的特征来表达输入。从而达到数据降维的效果。而将稀疏自编码网络用于手写体数字识别和人脸图像识别的实验也表明,稀疏编码网络具有很好的降维功能。
本文在介绍稀疏编码深层神经网络和它的结构以及工作原理的基础上,主要利用手写体数字和人脸图像数据库来检测稀疏自编码网络对高维数据的降维效果。
1 稀疏自编码网络结构和工作原理
1.1 稀疏自编码机
稀疏自编码机结构和自编码机结构大体相同,如图1所示,自动编码机将数据输入到解码器中得到一个输入的表达信息,并通过调整参数使这个信息与原始数据误差变小,从而达到对原始输入数据的良好表达,不同的是稀疏自编码机在该基础上加入了稀疏编码算法。
稀疏编码算法其实就是寻找一些基础特征来更高效地表示样本数据,它是一种无监督的学习方法。即找到一组基向量φi,使得能采用这些基向量线性的组合来表示[8]输入向量X:

图1 稀疏自编码机
换句话说就是用一组基的线性组合来表示一个信号,而且尽可能少的几个基就可以将信号表示出来。通过实验表明绝大部分感官数据,例如自然图像,都可以用少量基本元素的线性组合来表示。所以选择具有稀疏性的分量来表示高维数据可以在不丢失高维数据本质特征的基础上减少数据的维数。
虽然PCA技术也能方便地找到一组基向量来表达高维数据,但是稀疏算法能够找到一组更好的基向量。它们能够更加有效地挖掘高维数据的本质特征,并通过少量的特征来表达数据。
1.2 稀疏自编码网络
稀疏自编码网络结构如图2所示,整个系统由多个稀疏自编码机构成(虚框为一个稀疏编码机)。

图2 稀疏自编码网络结构
稀疏自编码网络工作原理如下:首先初始化编码器的权值ω1,…,ωn,然后给定一组样本数据[χ1,χ2,…],通过稀疏编码算法训练学习得到一组基[φ1,φ2,…],接着通过这组基向量得到对样本数据[χ1,χ2,…]的稀疏表达向量[α1,α2,…]。然后对编码网络进行多次训练,使原始训练数据与重构数据之间误差达到最小。最后利用反向传播误差导数的链规则,很容易得到期望的梯度值,这样就可以将稀疏自编码网络的权值调节到最佳。
2 稀疏自编码网络的实现
2.1 对Mnist数据集的实验
为了表明稀疏自编码网络能够有效地对数据降维,利用Mnist数据集来训练一个稀疏自编码网络并在网络最后接入分类器,通过Matlab软件仿真来观察识别率,进而反映稀疏网络对原始数据的稀疏表达,也就是对数据降维的效果。Mnist数据集包含0到9不同种手写体数字图片,如图3所示,其中训练数据60000张,测试数据10000张。图片分辨率均为28×28。

图3 部分Mnist数据库图像
首先对训练图片进行归一化,则每一张图片变为784维,则训练样本数据归一化为60000×784的矩阵,如图4所示。

图4 样本数据矩阵(部分)
由于样本包含10类,为方便进行分类,将样本最终降到维数为10,则稀疏自编码网络各层大小依次为784-500-100-10。然后利用稀疏编码算法来对网络权值进行初始化:⑴首先随机赋予网络权值初值;⑵对每个隐含层逐个进行无监督学习,使得这些初始权值能尽可能接近最优解(如图5所示)。

图5 网络权值初始化和训练后数据
接着通过多次执行反向传播算法来调整网络权值,使得网络达到最佳状态,这样稀疏自编码网络对原始数据进行了稀疏表达,也就是降维。得到的稀疏表达向量如图6所示。
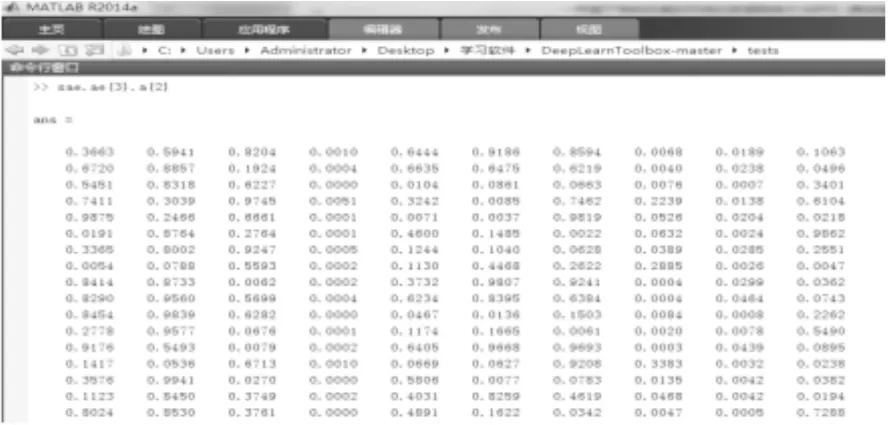
图6 稀疏表达向量
最后用获得最优权值的网络对10000张测试图片进行分类识别,识别率计算公式为

得到的结果如表1所示。
由表1可知,稀疏自编码网络可以较好地识别手写体数字,而且随着迭代次数的增加,识别率提高,由此可知稀疏自编码网络可以对Mnist数据集较好地降维。

表1 Mnist数据集识别结果
2.2 对人脸识别的实验
为了表明稀疏自编码网络不仅能够有效地对数据降维,而且与传统的方法比较,稀疏自编码网络有更好的降维效果。采用ORL人脸图像库进行实验,通过几种常见的降维方法和本文引入的稀疏自编码网络对训练图像进行降维,并利用测试集对比识别率来验证本文方法的可行性。
ORL人脸图像库是由英国剑桥大学工程部在不同时间、光照、面部表情下对40个人进行拍摄,每人10幅,一共400幅灰度人脸图像构成的,每幅图像的分辨率是112×92(如图7所示)。本文取每个人的前5幅图,共200幅图组成训练图像数据库,后5幅图为测试数据集。

图7 部分ORL数据库人脸图像
人脸识别的关键在于将人脸图片的大量冗余信息去除,从中找到具有代表性的、与其他类有明显差异的特征,所以降维的好坏直接影响到人脸识别的效果。
首先采用传统的降维方法进行人脸图像的降维,通过实验表明:PCA和LDA降维方法在子空间维数为60时识别率最大,达到79%和80.5%;ISOMAP算法在子空间维数为12时取得89.5%的识别率;而LLE算法在子空间维数为14时取得86.5%的识别率。
本文采用的稀疏自编码网络由于训练集图片像素为112×92,因此网络结构变为112×92-2576-500-100-40,与上个实验一样,首先通过归一化将112×92的图像转化为10304维实向量,不同的是模型最后一层将图像分为40类,因此将维数降维40。然后通过稀疏编码算法对网络进行训练(图8为训练得到的稀疏向量)。最终识别率达到了94.5% (图9为仿真结果)。

图8 ORL训练图片稀疏表达向量

图9 人脸识别仿真结果
表2为传统降维方法和本文降维方法对ORL人脸图像库的实验结果对比。

表2 ORL人脸识别实验结果对比
从表2可看出,线性降维方法PCA和LDA方法虽然取得了接近80%的识别率。但PCA对图像的光照的变化鲁棒性不理想,一旦光照发生明显改变,识别率就会受到很大的影响[9]。而LDA算法需将人脸图像矩阵转化为列向量或者行向量,这样就会增加运算的复杂性,容易导致矩阵奇异[10-11],从而影响识别率。而作为非线性降维方法的ISOMAP和LLE算法,取得了超过85%的识别率,原因在于人脸图像是一种由光照、表情等变量构成的流形非线性结构[12]。而本文引入的稀疏自编码网络(SAE网络)通过稀疏编码理论对人脸的数据进行了抽象表达,去除了图像的冗杂信息,在将数据降维的同时保留了人脸的主要特征,所以取得了接近95%的识别率。
3 结束语
根据稀疏理论算法,改进了自编码网络,在自编码网络的基础上加入稀疏算法,用以挖掘高维连续数据的抽象特征,去除冗余信息,从而达到数据降维的作用。将稀疏自编码网络用于手写体数字数据识别和人脸图像识别的实验表明,稀疏自编码网络对图像数据具有很好的降维功能。而如何快速地对更高维度的数据降维将成为下一步研究重点。
[1]Hotelling H.Analys is of a complex of statistical variables into principal components[J].Journal of Educational Psychology,1933(24):417-441.
[2]胡昭华,宋耀良.基于一种连续自编码网络的图像降维和重构[J].数据采集与处理,2010,25(3):310-323.
[3]胡昭华.基于粒子滤波的视频目标跟踪技术研究[D].南京:南京理工大学,2008.
[4]Roweis S T,Saul L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290 (5500):2323-2326.
[5]Tenenbaum J B,Silva V de,Langfo rd J C.A global geometric framework for nonlinear dimensionality reduction[J].Science,2000,290(5500):2319-2323.
[6]Rahimi A,Recht B,Darrell T.Learning to transform time series with a few examples[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(10):1759-1775.
[7]Liang W,David S.Learning and matching of dynamic shape manifolds for human action recog nition[J].IEEE Transactions on Image Processing,2007,16(6):1646-1661.
[8]尹远,廖敏江,李校林.基于无监督学习的行人检测算法[J].广东通信技术,2015(2):43-47.
[9]张珍.基于数据降维的人脸图像检索及识别[D].天津:河北工业大学,2011.
[10]张博.基于2DLDA的人脸识别快速算法研究[J].电脑知识与技术,2009,5(1):186-188.
[11]温福喜,刘宏伟.基于2D-PCA和2D-LDA的人脸识别方法[J].计算机应用研究,2007,24(8):201-203.[12]胡昭华,宋耀良.基于Autoencoder网络的数据降维和重构[J].电子与信息学报,2009,31(5):1189-1192.
(责任编辑:马金发)
Reducing the Dimensionality of Data with Sparse Autoencoder Network
ZHU Xiaotian,ZHANG Yanzhu,WANG Fandi
(Shenyang Ligong University,Shenyang 110159,China)
High-dimensional data of "dimension disaster" problem has restricted the machine learning,pattern recognition,and many other research developments in research field.So the dimension reduction method becomes one of the current research hotspots,which reduces the characteristic of high dimensional projection into low-dimensional space.The Sparse autoencoder network can convert high-dimensional data to low-dimensional codes by training a neural network with multiple hidden layers,which solves the problem of high-dimensional data’s lower recognition rate by large dimension effective.Sparse autoencoder network has good effect on handwritten digit image recognition and face image recognition.Simulation results show that the sparse autoencoder network can convert high-dimensional data to low-dimensional codes effective.
high-dimensional data dimension;sparse coding;image recognition
2015-07-17
朱啸天(1990—),男,硕士研究生;通讯作者:张艳珠(1971—),女,副教授,博士,研究方向:目标识别,分数阶控制,智能算法。
1003-1251(2016)05-0039-05
TP391
A

