大数据背景下政府补偿与企业努力程度关系的博弈研究
祖 峰,刘力钢,李 昕
(1.辽宁大学商学院,辽宁沈阳 110136; 2.渤海大学管理学院,辽宁锦州 121013)
大数据背景下政府补偿与企业努力程度关系的博弈研究
祖 峰1,2,刘力钢1,李 昕1,2
(1.辽宁大学商学院,辽宁沈阳 110136; 2.渤海大学管理学院,辽宁锦州 121013)
为了研究政府补偿与企业努力程度的关系,通过分析大数据决策系统构建与运行中政府与企业的合作方式,基于博弈论中的“委托-代理”理论模型,对大数据决策系统中政府与企业的合作关系进行了博弈分析,并设计了政府对企业补偿函数,即政府补偿与企业努力程度的函数关系,以企业与政府双方的利益最大化为基础,通过数值仿真分析的方法,得到博弈的均衡解——企业最优的努力程度和政府补偿,旨在为政府和企业的合作提供决策支持。
决策论;企业与政府博弈;大数据;委托代理;补偿函数;努力程度
祖 峰,刘力钢,李 昕. 大数据背景下政府补偿与企业努力程度关系的博弈研究[J].河北工业科技,2016,33(5):359-364.
ZU Feng,LIU Ligang,LI Xin.Study on the game of relationship between government compensation and the level of firms’ effort under the background of big data[J].Hebei Journal of Industrial Science and Technology,2016,33(5):359-364.
企业向政府缴纳税收,政府制定政策,维护企业发展的宏观环境,以保证和促进企业成长[1]。 中国政府对经济的主导地位导致了政企关系是支配与被支配的关系,企业所面临的不仅仅是企业内部的治理结构问题,更重要的是企业与政府之间的政治经济关系问题[2]。企业为谋求有利于自己的市场环境而影响政府政策法规制定过程的策略被称为企业政治战略[3],目的是依靠政府所具有的政治能力帮助企业实现自己的目标。中国企业特别是民营企业对政治关联的热衷甚至高过了自身的能力建设[4]。
大数据及其分析有效拓展了政府决策的主体范围,使得政府能够不再依据于传统经验和主观性的直觉做出决策,而是收集大量、实时的数据信息,以提升政府的预测准确度。这种开放式数据的分享与全样本的数据分析模式,使政府决策变得更为客观与透明,政府决策依据的变化趋势是“让数据说话”,这也为政企合作提供了新的契机。由于政府在数据量、数据处理和分析能力等方面的局限性,迫切需要大数据价值链上的企业的支持,共建决策系统。由此政企的关系转化为一种新型“委托-代理”关系,企业努力为系统的建设和运行提供服务,政府给企业提供补偿。那么政府应该提供怎样的补偿水平,以使企业的努力程度既能满足自身利润的最大化,又能达到政府的期望值?这些正是本文要解决的问题。
1 理论回顾
GRADUS[5]认为企业缴纳的税率与企业的投资及与企业未来缴纳的税收水平之间存在着一种关系,若缴纳税收增加则会降低投资水平,进而导致企业未来缴纳的税收水平的下降,因此应权衡现有的税收收入、企业投资水平、未来的税收收入三者之间的关系,由此GRADUS根据企业与政府之间的相互作用关系构建了一个微分博弈模型,以处理时间不一致性问题。
彭正银等[6]提出在“双轨制”阶段即政府计划与市场导向转轨阶段,企业与政府之间必存在博弈关系,政府既可以通过市场调节引导企业,又可以通过行政手段干预企业,由此提出了政府企业的双轨制动态博弈过程模型。
目前针对企业与政府的博弈方面的研究主要集中于以下几个方面。一些学者针对政府对企业的监管行为进行了一系列的博弈分析,提出企业的违规收益与监管力度之间存在着相互关系[7-8]。刘雯[9]提出在企业的运营过程中,如果企业通过违规行为所获收益小于其正常运营所获收益越多,则企业发生违规行为的可能性就越小;同时政府的监管程度越高,企业发生违规的可能性亦越小。另有些学者就政府与企业关于社会责任方面的博弈进行了研究,伍旭中[10]认为企业履行其社会责任既是为了回报社会、政府等利益相关者,又是为了获得他们的认同,同时由于地方政府从自身利益行为出发,往往对不履行社会责任的企业不予监督,因此中央政府需要加大对这种地方政府的惩罚和激励力度;章辉美等[11]针对汽车企业的社会责任问题,应用完全信息动态博弈模型,指出企业履行社会责任的概率与企业履行社会责任时所付出的成本有直接关系[12]。还有一些学者关注于企业与政府之间关于研发补贴方面的博弈分析[13],史安娜等[14]认为不同类型的企业从研发中获得的收益不同,其研发的积极性也不同,这致使政府对企业的研发补贴政策产生的效用亦有差异,因此政府应改变其传统的“选择性”资助方式,对不同企业的研发活动进行动态资助;吴晓园等[15]引入了完全不完美信息动态博弈模型,发现企业技术创新活动的开展取决于其创新所获得的相应收益、自身的创新能力和竞争对手的创新能力及政府的研发补贴的激励性等。
综上可知,众多学者在研究企业与政府的关系时未考虑信息技术的应用对二者关系的影响,亦脱离了时代背景。在大数据的时代背景下,政府和企业的关系不再是“领导与被领导”关系,而是一种基于“委托-代理”关系的博弈,这是政企合作的新趋势,如“云上贵州系统平台”等项目。
笔者从大数据的特征及思维模式出发,论证了政府决策依据改变的动因,展望了企业顺势改变其政治战略的发展趋势,指出在大数据决策系统的构建及运行中政府与企业之间形成了新的博弈合作关系。通过构建大数据决策系统中政企委托-代理模型,以企业与政府的双方利益最大化为基石,设计政府对企业补偿函数以及政府补偿与企业努力程度的函数关系,帮助企业选择有利于双方利益最大化的策略。
2 政府与企业共建大数据决策系统的合作关系分析
在大数据时代背景下,政府决策依据已由传统的“会议式”和“听证式”向“数据式”的方式转变,政府需要更为真实的全样本数据源,最专业的数据采集、分析与处理技术,来为公共事业管理或经济政策的制订服务。而企业,特别是大数据价值链上的企业,其在数据的采集、分析与处理上的专业经验与能力正是政府所渴求的。因此,在新的大数据决策系统中政府已非传统意义上的所谓的“领导者”,其身份已经发生了转变,政企之间已经产生了一种全新的合作模式。
首先,在大数据技术及应用得到不断发展的今天,企业已经完全成为一个相对独立的追求自身利益最大化的利益个体。拥有大数据技术的企业,由于其技术的重要性和关键性,其更具有活力和独立性。将大数据应用于政府与企业的决策中,企业与政府的关系已从传统的“父子”关系,转变为了合作关系,但其所追求的根本目标是自身经济收益的最大化,本质上并未考虑决策系统的优劣,这也是由本文提到的“理性人”假设所决定的。
其次,政府由“领导者”转变成为“合作伙伴”。在大数据决策系统中,企业的决策往往受到来自于政府的决策的影响,即在政府决策后作出决策,企业为了追求自身利益最大化而往往采取与政府期望背道而驰的决策行为,进而造成企业与政府之间的合作效率低下,甚至会导致合作的失败。
政府与企业之间的合作,属于“委托-代理”关系,在该关系中政府为委托人,企业为代理人。政府的期望目标收益受到企业行为的影响。在当前的市场经济中,政府不能通过直接干预手段影响企业行为,且由于信息的不对称性,使得政府无法深入了解和掌握企业的相关“自然条件”,因此,政府只能通过相应的政策手段来影响企业之后所采取的决策行为。
3 政府与企业共建大数据决策系统的博弈模型的构建
3.1 模型参与主体分析与基本假设
3.1.1 模型参与主体分析
由于政府在大数据决策系统中的主导地位,以及其对一些大数据价值链企业的技术依赖性,因此政府和企业在大数据决策系统中存在“委托-代理”关系的合作模式,本研究须对相关概念加以界定。
1)参与人 文中的参与人指大数据决策系统中的政府及与政府合作的企业。其中政府是大数据决策系统的需求者和倡导者,拥有数据资源,但缺少数据分析和处理的技术和经验;这里指的企业是拥有大数据分析、处理和数据挖掘等技术能力的企业。
2)参与人的策略 政府和企业在采取的策略过程中都存在2种可选择的方式,即对于政府而言,存在委托与否的2种策略;对企业而言,存在是否参与以及若参与后是否努力的策略。
3)参与人的支付 政府的支付为从大数据决策系统而获得的净收益,即大数据决策系统的产出减去政府对系统建设和运营的投入。文中企业的支付可以认为企业通过参与并努力与政府合作共创大数据决策系统的净收益,即企业从政府获得的补偿收益减去企业的行动成本。
4)委托人和代理人 文中将大数据决策系统中的政府设定为委托人,将有能力或意愿与政府合作共建大数据决策系统的企业设定为代理人。
3.1.2 模型的基本假设
1)参与人行为假设 在大数据决策系统中,将政府和企业均假设为理性的“经济人”,即参与各方的行为活动均以实现各自利益最大化为己任[6]。此时,企业作为一个理性人,它的目标就是赢利,收益最大化为其出发点。政府则需要选择最优的策略以保证在与企业合作中自身收益的最大化。
2)信息不对称性 本文是基于“委托-代理”理论以分析在大数据决策系统中的政企合作关系。政府作为系统中的“委托人”不能拥有作为“代理人”的企业的私人信息,如参与合作的意向,参与后工作的努力程度等,而企业却拥有完全的私人信息,因此存在着信息的不对称。
3)道德风险的存在 道德风险指代理人从事不适当或“不道德”行为的风险或“危险”[14]。由于博弈双方存在不对称的信息,拥有私人信息的企业方为实现自身收益最大化,可能会利用这一优势损害不具有私人信息的政府方的利益,如企业工作不够努力以降低成本,但政府并不知道企业是否足够努力,这就是由于信息不对称而导致了带来的道德风险的存在。
4)忽略产权因素 笔者在研究过程中为简化过程,将产权问题忽略,由于“委托-代理”模型的参与主体是完全对称的各方,因此政府与企业之间也存在地位上的对称性,即当企业与政府的位置发生互换时,并不影响委托方的决策,即补偿函数不发生变化。
3.2 模型的构建

图1 政府与企业博弈树Fig.1 Game tree between government and firm
依据上文假设,基于“委托-代理”模型的不完全信息动态博弈的参与者只有企业和政府,政府为委托人,企业为代理人,两者的博弈过程如图1的博弈树所示。委托人(政府) 首先行动,面临2种策略,即委托企业或不委托企业与其合作共建大数据决策系统。如不委托则博弈终止,本文只讨论政府采取委托策略时与企业的博弈过程。如委托,政府提供合同,即补偿函数,代理人(企业)面对政府的委托邀请,可采取参与与否2种策略,如企业选择不参与则博弈终止;如企业选择参与,可选择2种策略:努力或不努力,然而企业的策略和自然状态政府是观测不到的,如进入、退出系统壁垒的改变程度,技术环境等,因此政府只有在行动之初,通过设计有效的补偿函数以诱导企业在博弈中选择自己期望的策略,最终实现使政府和企业双双实现自身利益最大化的纳什均衡状态。下面基于“委托-代理”理论,将此博弈过程模型化,帮助政府找出既满足自身效用最大化,又满足企业参与约束和激励相容约束的补偿函数。
文章用A来表示企业所能够采取的行动组合集,a∈A,a表示企业某一特定行动。为了分析的便利性,文中假设a为企业即代理人的工作努力程度的一维变量。令θ为外生随机变量,该变量是不受企业即代理人和政府即委托人所控制的“自然状态”,Θ是θ的取值范围,令θ在Θ上的分布函数为G(θ),θ在Θ上的密度函数为g(θ),其中θ是连续变量;若θ只有有限个可能值,g(θ)为概率分布。企业在选择某一特定行动a之后,θ作为外生变量得以实现,令x(a,θ)为可观测结果,其中a和θ为可观测结果x的解释变量,即存在x(a,θ),说明a和θ共同影响观察结果x,同时令π(a,θ)为系统产出,a和θ亦是π的解释变量,即存在π(a,θ),其中系统产出π(a,θ)的直接所有权属于政府即委托人。假定π是a的凹函数,且严格递增,即θ在给定状态下,企业的努力程度越高,系统的总产出越高,但其努力的边际产出率表现为递减。观测结果x(a,θ)可能为向量,且包含系统产出π。文章假定系统的产出为可观测变量,且只有π是可以观测的,即x=π。政府需设计激励合同即政府对企业的补偿函数s(π),依据可观测的π对企业进行奖惩。
假定政府与企业的期望效用函数分别为v(π-s(π))和u(s(π))-c(a),假定v′>0,v″≤0;u′>0,u″≤0;c′>0,c″>0;c(a)是企业行动或者努力程度的负效用,即政府和企业都是风险规避者或风险中性者,努力的边际负效用是递增的。
政府的期望效用函数可以表示为
(P) ∫v(π(a,θ)-s(π(a,θ)))g(θ)dθ。
政府所面临的即是如何得到a和s(π),以使得政府的期望效用函数最大化。此时,政府面临着来自于企业的约束。


第2个约束是企业的激励相容约束,若假设a是政府与企业合作过程中政府对于企业所期望的努力程度的取值,a′∈A是企业可选择的任何努力程度,那么当企业选择a时所获得的期望效用大于a′时的期望效用时,企业才会选择努力程度a。激励相容约束的数学表达式如下:
(IC) ∫u(s(π(a,θ)))g(θ)dθ-c(a)≥
∫u(s(π(a′,θ)))g(θ)dθ-c(a′),∀a′∈A。
政府所面临的问题是得到a和s(π)最大化期望效用函数(P),满足约束(IR)和(IC),
即
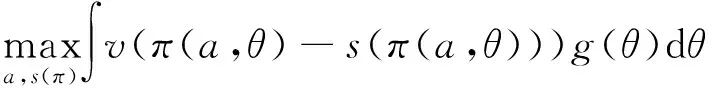
s.t.

(IC) ∫u(s(π(a,θ)))g(θ)dθ-c(a)≥
∫u(s(π(a′,θ)))g(θ)dθ-c(a′),∀a′∈A。
3.3 模型的改进

改进后模型的参与约束如下:

激励相容约束表示如下:
(IC) s(π(a))-c(a)≥s(π(a′))-c(a′),a′∈A是企业可选择的任何努力程度。
改进后模型的数学表达归纳如下:

(1)
s.t.

(2)
(IC) s(π(a))-c(a)≥
s(π(a′))-c(a′), ∀a′∈A。
(3)
3.4 模型的求解
首先看参与约束式(2)。

由理性人假设,政府希望最小化补偿函数,则有:

即

(4)
然后,将式(4)代入目标函数(1),得到:

而


解得的a*就是政府所希望企业的努力程度。
之后,激励相容约束式(3),将a*代入式(3),则有:
s(π(a*))-c(a*)≥s(π(a′))-c(a′)⟹
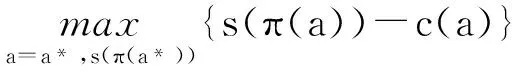
{s(π(a*))-c(a*)}′=0,
可解得满足条件{s(π(a*))-c(a*)}′=0的补偿函数中的待定参数k和b的值,进而得到补偿函数s(π(a))。
4 模型的数值仿真分析
为了验证模型的可行性和求解过程,本文采用数值仿真分析,将必要的已知条件和函数在符合模型假设的前提下加以赋值和设定,得到问题的均衡解。
由模型假设大数据决策系统的产出π与企业努力程度a的函数是“严格递增的凹函数”,而且实际情况决定了函数π(a)必然经过点(0,0),即若企业的努力程度为0,系统产出亦为0。
设:π(a)=3ln(a+1)+ξ,a∈[0,∞),ξ为随机扰动项;
设政府提供给企业的补偿函数:s(π)=kπ+b,k与b为待定参数。

根据上文建立的政府与企业合作的博弈模型,问题的求解过程如下:
首先,将相应的预先设定好的函数及数值代入参与约束式(1),得:
s(π(a)) =kπ(a)+b≥0.25a2+40,
理性政府会选择端点值作为补偿,则有:
s(π(a))=k[3ln(a+1)+ξ]+b=
0.25a2+40。
(5)
然后,将π(a)和式(5)代入目标函数(1)中,即最大化政府的支付,得:

(3ln(a+1)+ξ-0.25a2-40)′=0
解得a1=2,a2=-3(舍去)。
因此,a=2就是能够使政府在博弈中的支付最大化的努力程度a*。但a*必须要满足使企业的支付最大化的条件才能实现博弈的均衡,接下来通过考虑企业的支付最大化的条件进一步求解。
最后,将设定的函数代入企业的支付表达式,则有:
s(π(a))-c(a)=
k[3ln(a+1)+ξ]+b-0.25a2。
若使其最大化可以表示如下:
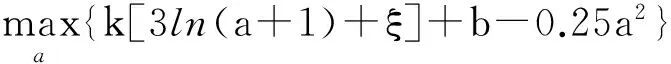
{k[3ln(a+1)+ξ]+b-0.25a2}′=0⟹
6k=a(a+1)。
(6)
将a*=2代入式(6),解得k=1。
将a*=2,k=1代入式(5),则有:
1×[3ln(2+1)+ξ]+b=0.25×22+40,
解得b=41-3ln3-ξ,将k,b代入s(π(a)),则政府提供给企业的补偿函数为
s(π(a))= 1×[3ln(a+1)+ξ]+41-3ln3-ξ=

(7)
式(7)即是具有激励作用的政府补偿函数的最终解,此时的企业的努力程度a*,既满足政府支付的最大化,又满足了企业支付的最大化,为政府和企业合作博弈的均衡解。如果政府在与企业合作中提供上述的补偿,企业会付出a*水平的努力程度,也正是政府所期望企业为大数据决策系统所贡献的努力程度,对于政府、企业及系统产出都是最优解。
5 结 论
国内对大数据的应用尚处于认知阶段,虽然一些拥有大数据资源的电子商务企业已经开始运用大数据的分析和处理服务于市场需求,但政府运用大数据决策系统服务于社会管理与经济政策则刚刚起步。由于大数据思维模式与生俱来的优势和它对传统统计学思维颠覆性的挑战,大数据决策的科学性与准确性已越来越被学术界认可,同时,政府亦认识到大数据的运用将改善其社会管理水平,使政策的制定更为科学、合理和具有说服力。基于此背景,本文探讨了企业政治战略的转变思路,分析了在未来的大数据决策系统中政府与企业的合作方式,并以博弈论中的“委托-代理”理论模型为基础,对大数据决策系统中政府与企业的合作关系进行了博弈分析。通过构造系统产出函数π(a)与政府补偿函数s(π)=kπ+b,经改进后的“委托-代理”博弈模型求解,最终得到政府补偿s与企业努力程度a的函数关系s(a),即在大数据决策系统中,基于政企利益最大化原则,企业的努力程度越高,企业的收益越大,政府对企业的补偿程度越高,但努力的边际产出率是递减的。
尽管关于政府在大数据决策系统应用方面尚无数据可以利用,但政府与企业的合作关系的博弈分析却可以高度概括为抽象的理论模型,即企业努力程度影响系统产出,进一步影响到企业补偿的作用过程。文中的数值仿真分析中数值与函数的设定满足模型的合理化假设,并不影响其中均衡规律的发掘。本文的贡献在于所得到的企业努力程度与政府补偿的的函数关系是满足企业和政府双方受益最大的博弈均衡结果,可为政府给予企业补偿提供理论决策依据,可为后续的政企合作博弈研究奠定基础,希望能对政府制定政策起到一定的指导与借鉴作用。
[1] SCHOCHET G J, Thomas hobbes on the family and the state of nature[J]. Annali Di Ottalmologia E Clinica Oculistica, 1967,82(3):1149-1154.
[2] 郭士倜, 宁艳丽. 地方政府行为与民营企业发展的关系研究——一个动态博弈分析[J].求索, 2011(4):60-62.
[3] HILLMAN A,KEIM G. International variation in the business-government interface: Institutional and organizational considerations[J]. The Academy of Management Review, 1995,21(1):193-224.
[4] 杨其静. 企业成长:政治关联还是能力建设?[J].经济研究,2011(10):54-66.
YANG Qijing. The growth of enterprises:To build political connections or capability?[J]. Economic Research Journal,2011(10):54-66.
[5] GRADUS R H J M. A differential game between government and firms:A non-cooperative approach[J]. Journal of Economics, 1989,50(3):237-256.
[6] 彭正银, 宋蕾. 企业与政府的双轨博弈分析[J]. 中国软科学, 2003(12):77-80.
PENG Zhengyin, SONG Lei. Dual-track game analyses on firms and the state[J]. China Soft Science, 2003(12):77-80.
[7] 钟黎川. 服务型政府背景下地方政府与微观主体互动行为研究——以博弈论为视角[J]. 经营管理者, 2009(13):94-95.
[8] 左伟. 基于食品安全的企业、监管部门动态博弈分析[J].华南农业大学学报(社会科学版), 2009,8(3):62-68.
ZUO Wei. Dynamic game between enterprises and supervision department in view of food safety[J]. Journal of South China Agricultural University(Social Science Edition), 2009,8(3):62-68.
[9] 刘雯. 基于博弈论的政府企业关系探讨[J]. 山西高等学校社会科学学报, 2010,22(9):56-58.
LIU Wen. A study of the relationship between government and enterprise based on game theory[J]. Social Science Journal of Universities in Shanxi, 2010,22(9):56-58.
[10]伍旭中. 政府治理、社会责任投资与企业社会责任:博弈与实现机制[J].安徽师范大学学报(人文社会科学版), 2012,40(2):185-191.
WU Xuzhong. Government governance, social responsibility investment and corporate social responsibility: Game and implementation mechanism[J].Journal of Anhui Normal University (Hum & Soc Sci), 2012,40(2):185-191.
[11]章辉美, 邓子纲. 基于政府、企业、社会三方动态博弈的企业社会责任分析[J].系统工程, 2011,29(6):123-126.
ZHANG Huimei, DENG Zigang. Analysis of corporate social responsibility based on three-side dynamic game between government, society and enterprises[J]. Systems Engineering, 2011,29(6):123-126.
[12]徐雨森, 秦曦, 李家波,等. 企业社会责任履行与政府监管的博弈分析[J].现代管理科学, 2015(7):100-102.
[13]曼昆. 经济学原理(微观经济学分册)[M].6版.梁小民,梁砾,译.北京:北京大学出版社, 2012.
[14]史安娜, 李兆明, 黄永春. 工业企业研发活动与政府研发补贴理念转变——基于演化博弈视角[J]. 中国科技论坛, 2013(5):12-17.
SHI Anna, LI Zhaoming, HUANG Yongchun. Industrial enterprise's R & D activities and government’s R & D subsidy reform:Based on the evolutionary game theory[J]. Forum on Science and Technology in China, 2013 (5):12-17.
[15]吴晓园, 丛林. 企业技术创新策略与政府R&D补贴——基于不完美信息的动态博弈模型[J]. 科学学与科学技术管理, 2012,33(2):56-62.
WU Xiaoyuan, CONG Lin. Strategies of enterprise innovation and government R&D subsidy:Dynamic game analysis of imperfect information[J]. Science of Science and Management of S & T, 2012,33(2):56-62.
Study on the game of relationship between government compensation and the level of firms’ effort under the background of big data
ZU Feng1,2,LIU Ligang1,LI Xin1,2
(1. Business School, Liaoning University, Shenyang, Liaoning 110136, China;2.Management School, Bohai University, Jinzhou, Liaoning 121013, China)
In order to study the relationship between the government compensation and the firms’ effort, through analyzing the ways of cooperation between the government and the firms in big data decision system construction and operation, and based on game theory principal-agent theory model, the paper carries on the game analysis of government and firms cooperation in big data decision system. The government’s compensation function, that is, the relationship between the government compensation and the firms’ effort level is designed. For the maximum benefit of both the firms and the government, the paper gives out the equilibrium solution of the game-the firms’ optimal effort level and the government compensation by the method of numerical simulation analysis. The aim is to provide decision support for both the government and the firms.
decision theory; game between government and enterprises; big data; principal-agent; compensate function; level of effort
1008-1534(2016)05-0359-06
2016-06-02;
2016-07-02;责任编辑:张 军
国家社会科学基金(14BGL053);辽宁省社科联2015年度辽宁经济社会发展课题(2015lslktzijjx-6)
祖 峰(1978—),男,辽宁锦州人,讲师,博士研究生,主要从事企业战略管理方面的研究。
E-mail:lx4321@126.com
F270
A
10.7535/hbgykj.2016yx05001

