方钢管混凝土边框柱组合剪力墙关键性连接点剪力计算

张 刚,张延庆，魏婷婷

(1.北京工业大学建筑工程学院，北京 100124;2.中国建筑科学研究院，北京 100013)



方钢管混凝土边框柱组合剪力墙关键性连接点剪力计算

张 刚1,张延庆1，魏婷婷2

(1.北京工业大学建筑工程学院，北京 100124;2.中国建筑科学研究院，北京 100013)

针对方钢管混凝土边框柱组合剪力墙墙柱连接点处的抗剪键现无设计依据的问题，从构件整体性着手研究，建立合理的简化计算模型，借助弹性力学，分析其在水平荷载作用下墙柱连接点处的应力分布情况并导出剪力计算公式。通过与ANSYS有限元模型计算结果对比，验证了公式计算结果的正确性。

复合结构；方钢管混凝土柱；组合剪力墙；连接点；应力分布；抗剪键

张 刚,张延庆,魏婷婷.方钢管混凝土边框柱组合剪力墙关键性连接点剪力计算[J].河北工业科技,2016,33(5):410-414.

ZHANG Gang, ZHANG Yanqing，WEI Tingting.Shear calculating of critical connection points of composite shear wall with rectangular concrete filled steel tubular columns[J].Hebei Journal of Industrial Science and Technology,2016,33(5):410-414.

剪力墙结构采用现浇钢筋混凝土，整体性好，承载力及侧向刚度大，广泛应用于高层建筑中(组成核心筒的剪力墙是高层建筑抗侧力的主体)[1-2]。近年来，随着国民经济的飞速发展和科技水平的逐步提高，中国的建筑至高点被不断刷新，超高层对建筑结构的性能要求也日益苛刻。对此，国内外不少学者先后提出了不同形式的新型剪力墙，欲改善其整体性能。方钢管混凝土柱承载力高、延性好，在传统剪力墙两侧各设1根方钢管混凝土柱，通过抗剪键连接为整体，将两者的优点结合起来。这种组合剪力墙承载力高，抗震性能好，具有良好的应用前景[3]。研究人员通过大量低周反复加载试验对方钢管混凝土边框柱组合剪力墙进行了抗震性能研究，结果表明其抗震性能提升明显，并分析了轴压比、混凝土强度等因素的影响[3-5]。但是，对于此新型组合剪力墙而言，尚缺乏系统的理论研究，不便于关键性连接点的合理设计。本文从方钢管混凝土边框柱组合剪力墙在地震作用下的结构整体性着手研究，建立合理的简化计算模型，借助弹性力学分析其在水平荷载作用下，方钢管混凝土边框柱与混凝土剪力墙交接处的应力分布情况并导出计算公式，通过ANSYS验证公式的正确性，为此类组合剪力墙抗剪键的设计提供参考。

1 理论分析

初始模型参考王绍合[3]的试验，如图1所示。其中A为加载梁，B为方钢管混凝土边框柱，C为混凝土剪力墙，D为基础。组合剪力墙顶端承受竖直向下的均布荷载p，用于控制轴压比，左端受水平方向的推力F，底端固定。本文拟用半逆解法求解应力函数Φ[6]。将B，C两部分作为研究对象，不计体力，根据实际受力状态可将其简化为平面应力模型分析。如图2所示建立直角坐标系，具体参数见表1。图2中a为1/2墙长；e为方钢管边长；h为墙高；

μ0，μ1分别为B，C两种材料的泊松比；E0，E1分别为两种材料的弹性模量。水平推力F取试验极限荷载值乘以0.8的折减系数。

图1 试验模型Fig.1 Test model

图2 坐标关系Fig.2 Coordinate relation

表1 参数取值

上述简化模型处于弹性状态，运用圣维南原理将混合边界条件转化为应力边界条件[6-7]，结合数值模拟，将两侧边界应力分布予以修正，设定的边界应力分布如图3所示。

其中：

(1)

(2)

图3 边界应力分布Fig.3 Distribution of boundary stress

根据应力分量与应力函数Φ的关系逆推[6]，可得:

(3)

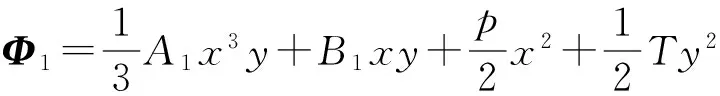
(4)

其中M0=2A0，M1=2A1。

接下来，通过边界条件确定系数A0，B0，A1，B1，T。

首先，在上边界剪应力积分值为F:

(5)

其次，边框柱外侧无剪应力:

(τxy0)x=a+e=0。

(6)

因为B，C部分材料不同，考虑接触面位移协调，则

(7)

将式(1)、式(2)分别代入式(5)—式(7)中，联立方程组，解得各系数如式(8)—式(12)所示：

(8)

B0=-A0(a+e)2,

(9)

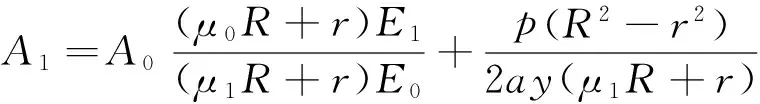
(10)

(11)

(12)

其中：

(13)

K=a3(μ0R+r)(1+μ1)-

3a3(μ0-μ1)(R-r)-

3a(1+μ0)(μ1R+r)(a+e)2。

(14)

将A0，B0，A1，B1，T代入式(1)、式(2)，即可得任何一点的应力分布。进一步，方钢管混凝土边框柱与混凝土剪力墙交接处的剪力为

(15)

代入系数表达式后积分，就是最终的剪力公式。因为系数表达式比较复杂，建议先赋值，得出具体的系数值，再代入积分计算。

2 数值分析

2.1 有限元模型

本节通过建立合理的ANSYS有限元模型，验证第1节应力边界的合理性和公式的正确性。所建模型如图4所示，参数按照表1输入，柱子和墙体分别赋予不同的材料属性。为了减小应力集中的影响，组合墙体上下两端稍作纵向延伸，作为缓冲区，并在底部附加基础[8-9]。划分单元后通过vglue命令使不同材料的单元节点共用，保证墙柱连接处位移协调[10]。定义表面效应单元[11-12]，在上边界分别加载水平方向和竖直方向的均布荷载，同时约束模型下边界为固定端。

图4 ANSYS模型Fig.4 ANSYS model

2.2 结果分析

按表1中参数取值给式(1)、式(2)中的系数赋值，即可得到该模型的应力分布表达式。分别令y=-1.0,-1.4,-1.8,-2.2, -2.45,-2.7，得到不同高度处的剪应力分布(见图5—图10)。

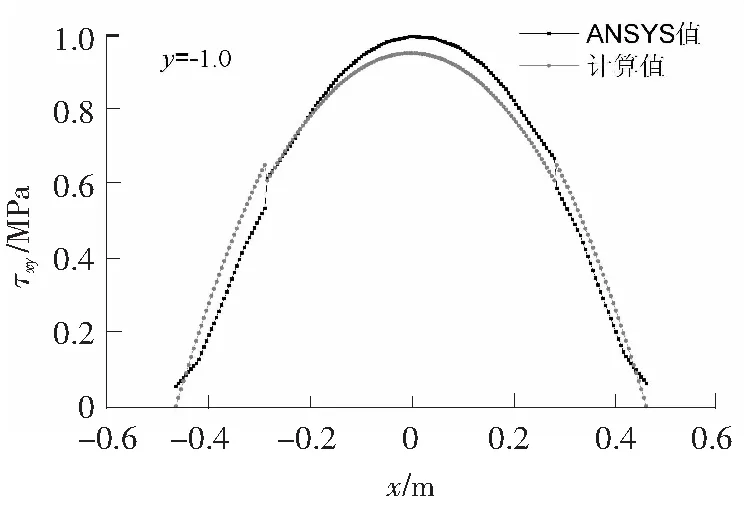
图5 y=-1.0处剪应力分布比较Fig.5 Comparison of shear stress distribution at y=-1.0

在ANSYS模型中运行Solve命令后，通过定义路径分别获取以上相应高度处的剪应力分布[13-14]，绘制于对应坐标图中，见图5—图10。

图6 y=-1.4处剪应力分布比较Fig.6 Comparison of shear stress distribution at y=-1.4

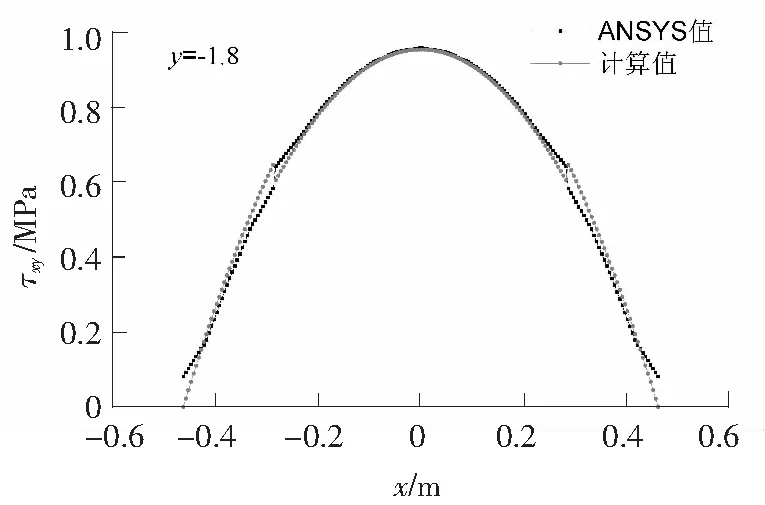
图7 y=-1.8处剪应力分布比较Fig.7 Comparison of shear stress distribution at y=-1.8

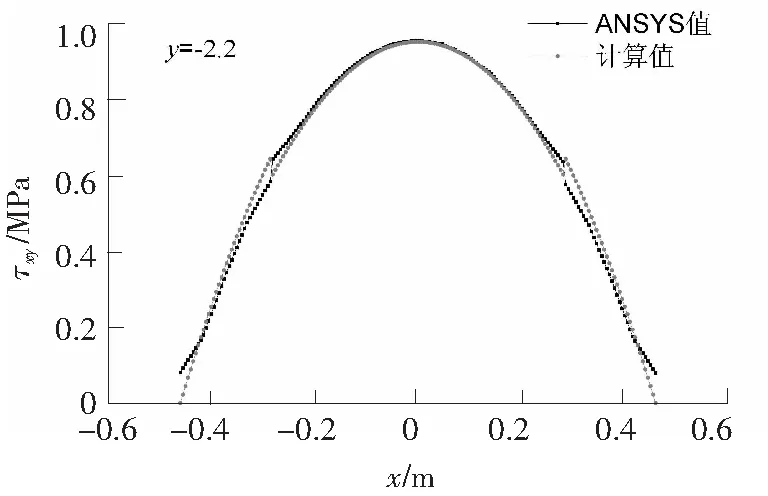
图8 y=-2.2处剪应力分布比较Fig.8 Comparison of shear stress distribution at y=-2.2

图9 y=-2.45处剪应力分布比较Fig.9 Comparison of shear stress distribution at y=-2.45

图10 y=-2.7处剪应力分布比较Fig.10 Comparison of shear stress distribution at y=-2.7

从图5—图10中可以看出：在模型的上下边界(y=-1.0,y=-2.7)处，因为应力集中的影响，剪应力分布曲线与公式计算所得的曲线在局部有一定差异，模型其他部分结果较为接近。因为在推导Φ的过程中做了一定简化，与实际受力存在误差，但最终计算公式Q并非直接用于工程设计中，而是作为设计参考，所以对于存在的误差可以忽略。此外，σx，σy两应力分量的应力分布也吻合较好。至此，可肯定第1节中假设的应力分布和推导出的应力函数Φ基本正确。

最后分析剪力公式(15)在x=±a处(墙柱连接点)的剪力值。在ANSYS有限元模型x=±a处定义路径，并对路径积分[15-18]得Q1左，Q1右，同时给式(15)赋值x=±a计算得到Q2，结果见表2。

表2 剪力值对比

显然，公式计算结果与数值模拟结果非常接近。

3 结 语

本文推导的剪力公式(15)主要用于求解方钢管混凝土边框柱组合剪力墙的墙柱连接点处的剪力，用于抗剪键的设计参考。尽管在推导的过程中做了一定简化，与实际受力存在误差，但本公式主要用于抗剪键设计时的参考，所以不影响实际应用。日后研究或应用方钢管混凝土边框柱组合剪力墙时，通过此公式，可以对抗剪键的受力大小有一个大概的预测，避免盲目设置。

针对第2节中剪应力在组合墙体上、下端处的应力集中现象，建议设计抗剪键时，在参考本文公式求出的剪力值的同时，亦要考虑组合墙体上、下端处的开裂设防，最好在上、下端处适当加强抗剪措施。

[1] 方鄂华,钱稼茹,叶列平.高层建筑结构设计[M].北京:中国建筑工业出版社,2003:12-15.

[2] 王崇昌,马克俭,粟秀文,等.钢筋混凝土剪力墙结构分析[M].贵州:贵州人民出版社,1989:1-4.

[3] 王绍合.方钢管混凝土端柱-混凝土组合墙体抗震性能研究与应用[D].北京:北京工业大学,2008.

WANG Shaohe. Experimental Study and Theoretic Analysis on the Seismic Behavior and Application of High-Rise Shear Wall with Concrete-Filled Rectangular Steel Tube Column in Both Ends[D]. Beijing: Beijing University of Technology, 2008.

[4] 王敏,曹万林,张建伟,等.钢管混凝土边框高强混凝土组合剪力墙抗震性能试验研究[J].地震工程与工程振动,2008,28(2):90-95.

WANG Min, CAO Wanlin, ZHANG Jianwei, et al. Seismic experimental research on high strength concrete composite shear wall with concrete filled steel tube colums[J]. Earthquake Engineering and Engineering Dynamics, 2008, 28(2):90-95.

[5] 曹万林,王敏,王绍合,等.矩形钢管混凝土边框组合剪力墙及筒体结构抗震研究[J].工程力学,2008,25(sup1):58-70.

CAO Wanlin, WANG Min, WANG Shaohe, et al. A seismic research of composite shear wall and core walls with rectangular concrete filled steel tube colums[J]. Engineering Mechanics, 2008,25(sup1):58-70.

[6] 徐芝纶.弹性力学[M].北京:高等教育出版社,2006.

[7] 杨桂通.弹性力学简明教程[M].北京:清华大学出版社,2013:58-63.

[8] 成锟.方钢管混凝土约束端柱组合剪力墙的力学性能分析[D].北京:北京工业大学,2009.

CHENG Kun. Nonlinear Analysis of Composite Shear Wall with Concrete Filled Steel Tube Columns[D]. Beijing: Beijing University of Technology, 2009.

[9] 于立彬,张延庆.轴压比对钢管混凝土边框组合剪力墙的影响[J].山西建筑,2010,36(17):53-55.

YU Libin, ZHANG Yanqing. Analysis of influence factors on anti-explosion performance of RC column with bond slip[J].Shanxi Architecture, 2010, 36(17): 53-55.

[10]韩淑芳,张延庆,赵磊.方钢管混凝土约束端柱组合剪力墙性能研究[J].河北建筑工程学院学报,2008,26(2):4-7.

HAN Shufang, ZHANG Yanqing, ZHAO Lei. The performance investigation of composite shear wall of concrete-filled and restrained end square tubular column[J]. Journal of Hebei Institute of Architecture and Civil Engineering, 2008, 26(2):4-7.

[11]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2005:479-485.

[12]何本国.ANSYS土木工程应用实例[M].北京:中国水利水电出版社,2011.

[13]曾攀,雷丽萍,方刚.结构的建模与分析[M].北京:机械工业出版社,2006:77-80.

[14]李波.ANSYS结构建模技巧[J].山西建筑,2007,33(5):76.

LI Bo. Modeling technology of ANSYS structure[J]. Shanxi Architecture, 2007, 33(5):76.

[15]陆新征,江见鲸.用ANSYS Solid65单元分析混凝土组合构件复杂应力[J].建筑结构,2003,33(6):22-24.

[16]魏炜.部分预应力混凝土受弯构件开裂截面应力计算[J].河北科技大学学报,2012,33(6):559-563.

WEI Wei. Stress calculation of cracking section of partially prestressed concrete bending member[J]. Journal of Hebei University of Science and Technology, 2012, 33(6): 559-563.

[17]刘明泉,李晓芝.钢绞线加固混凝土板的应力分析[J].河北工业科技,2016,33(3):230-234.

LIU Mingquan, LI Xiaozhi. Stress analysis of concrete slab reinforced by steel wires[J]. Hebei Journal of Industrial Science and Technology, 2016,33(3):230-234.

[18]谭燕秋，宫玉侠，吴欣.两边连接双层钢板剪力墙承载力性能研究[J].河北工程大学学报(自然科学版)，2013，30(4)：8-12.

TAN Yanqiu,GONG Yuxia,WU Xin.The bearing capacity performance of two-side connected steel-plate-steel shear wall[J].Journal of Hebei University of Engineering(Natural Science Edition),2013,30(4):8-12.

Shear calculating of critical connection points of composite shear wall with rectangular concrete filled steel tubular columns

ZHANG Gang1, ZHANG Yanqing1，WEI Tingting2

(1.College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China; 2.China Academy of Building Research, Beijing 100013, China)

Aiming at the problems of there being no design basis for the shear keys between the wall and column of the composite shear wall with rectangular concrete filled steel tubular columns, the paper starts the study with structural integrity, constructs a simplified calculation model, and with the help of elasticity, analyzes the stress distribution of at the connection points between the wall and the columns when the structure is under horizontal load, and derives the calculation formula of shear. By comparing with the calculated results of the ANSYS, the correctness of the formula is verified.

composite structure; rectangular concrete filled steel tube columns; composite shear wall; connection point; distribution of stress; shear key

1008-1534(2016)05-0410-05

2016-03-22;

2016-05-05；责任编辑：冯 民

张 刚(1990—)，男，山东潍坊人，硕士研究生，主要从事方钢管混凝土边框柱组合剪力墙方面的研究。

张延庆教授。E-mail:zhyq@bjut.edu.cn

TU398+.2

A

10.7535/hbgykj.2016yx05009