电动汽车锂离子动力电池分选方法研究
陈燕虹+吴伟静+刘宏伟+张振兆


摘 要:为了改善电动汽车电池组的不一致性,提高电池组的可用功率和容量利用率,以电池的不一致性机理分析为基础,分别对电池进行了传统分选、主因子分选和总因子分选.单体试验计算结果表明,总因子分选方法是最优的.接着在总因子分选结果的基础上运用模糊C均值聚类算法对电池进行了动态特性分选,试验结果表明:此分选方法能有效地改善电池组的不一致性.
关键词:车辆工程;锂离子动力电池;不一致性;多参数分选;动态特性分选
中图分类号:U463.63 文献标识码:A
文章编号:1674-2974(2016)10-0023-09
Abstract:In order to improve the consistency for lithium-ion power battery of electric vehicle, to raise the available power and the utilization ratio of capacity for the battery pack, this paper put forward a battery sorting method based on the inconsistency mechanism analysis of battery. Firstly, the traditional sorting method, the main factor sorting method and the total factor sorting method for battery were completed respectively, and the comparative results show that the total factor sorting method is optimal. Secondly, the dynamic characteristics sorting was carried by fuzzy c-means clustering algorithm based on the total factor sorting results. Finally, the sorting effect was verified through experiments and the result shows that this sorting method can improve the inconsistency for battery pack effectively, and has a certain practical significance.
Key words:vehicle engineering; lithium-ion power battery; inconsistence; multi-parameter sorting; dynamic characteristics sorting
为了满足驱动电机供电电压和整车续驶里程的要求,电池组需要通过上百节电池单体串联或并联而成.电池单体之间的不一致性会使电池组在使用过程中存在“木桶效应”,这种现象的存在会降低电池组的充放电效率,减少电动汽车的续驶里程.
目前,解决电池不一致性的技术措施主要有电池分选、电池均衡以及电池热管理等方法,本文针对电池分选方法进行研究.电池分选方法主要有单参数分选法、多参数分选法以及动态特性分选法,而多参数分选法与动态特性分选法相结合的方法是目前研究的趋势.
多参数分选法采用多个特征参数对电池进行分选.刘千杰等[1]通过4次充放电循环,以容量差1%、 电压10 mV、内阻2 mΩ以及充电恒流比1%以内为一档对电池进行分类,分选效果较好;吴生先[2]以容量公差为额定容量的±1%,开路电压公差为±10 mV,内阻公差为±0.5 mΩ,自放电公差为±5 mV,分选效果也较好;Jonghoon Kim等[3-4]针对电压均衡技术可能造成的电压一致而荷电状态不一致的情况,提出了一种基于容量和内阻来提高锂离子动力电池组的电压和SOC一致性的方法.但是上述多参数分选方法并没有对分选变量进行优化,分选变量之间存在的相关性会影响分选结果.
动态特性分选根据充放电曲线对电池进行分选.单毅[5]通过对充放电曲线采用层次聚类的方法得到电池之间的差异度,试验表明该方法的分选效果较好;闻涛等[6]提出了一种基于特征向量的电池分选方法,但是标准电压特征向量较难确定,增加了分选工艺实施的难度;苑风云[7]搭建了以SOC为纽带的电池等效电路模型,根据模型仿真得出的充放电曲线之间的相似性对电池进行分选;Raspa等[8]通过自组织图的方式根据电池的SOV变化来对电池进行分选.但是上述动态特性分选方法均没有考虑电池的其他参数,并且实施较为复杂.
本文提出了一种多参数分选与动态特性分选相结合的分选方法.多参数分选以统计学软件SPSS为基础,利用因子分析模块对分选变量进行优化,利用系统聚类模块分别对电池进行主因子分选和总因子分选;动态特性分选以电池的放电曲线为基础,通过MATLAB编程来实现模糊C均值聚类算法,从而实现对电池的分选.
1 不一致性分析
电池的不一致性,是指同批次、同规格、同型号的电池,在电压、容量、内阻以及自放电率等特征参数上所表现出的差异性.
锂离子动力电池的不一致性主要在生产、使用和储存过程中产生.生产过程中造成的电池不一致性会在使用和储存过程中被累积扩大,比如,容量不同的两节电池进行串联充放电,通过的电流是相同的,在相同时间内充放电容量是一样的,在容量小的电池达到其极限容量时,容量大的电池可能正处于未充满电或者未放完电的状态,这样就会造成能量浪费.如果反复进行充放电,则势必会使得容量小的电池始终处于深充深放状态,而容量大的电池始终处于浅充浅放状态,这样容量小的电池性能会越来越差,与容量大的电池的不一致性也会进一步加剧.
所以在电池使用之前采用合理的方法对其进行分选显得尤为重要.
2 多参数分选
本文首先以统计学软件SPSS为基础对电池进行多参数分选.
2.1 分选变量的获取
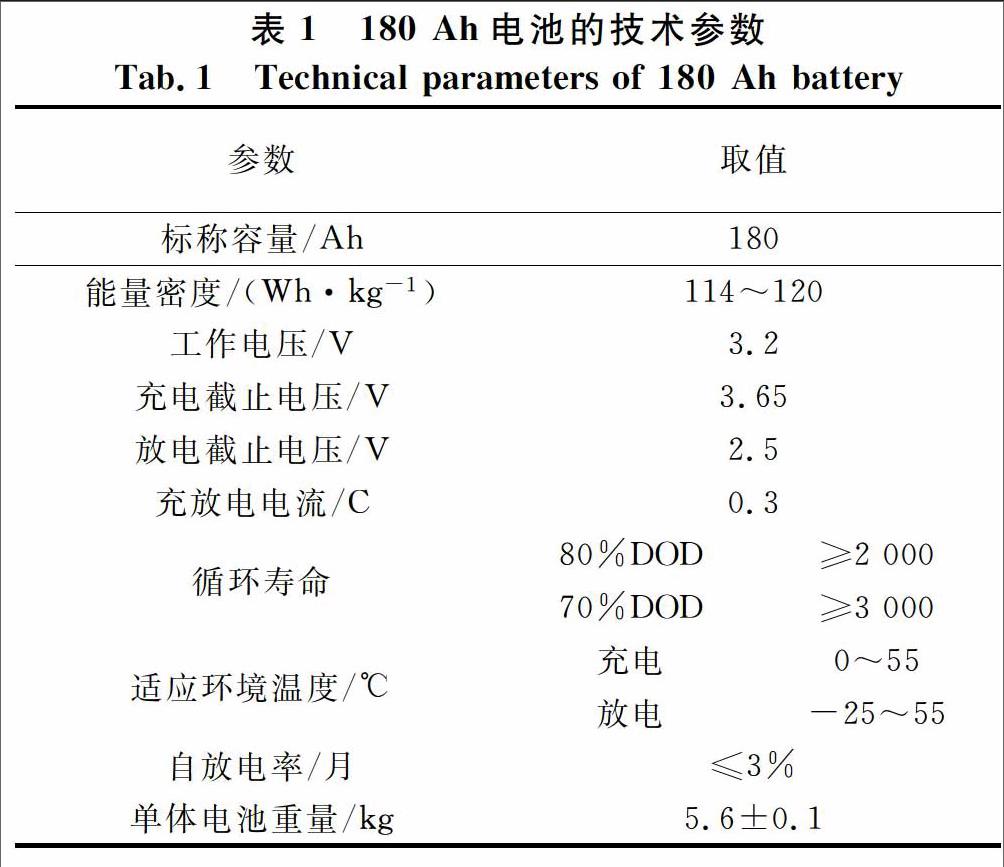
以100节180 Ah电池为研究对象来探究有效的电池分选方法,其技术参数如表1所示.
在进行多参数分选之前需要确定分选变量.分选变量可以以不一致性的表现形式为依据进行选择.另外,电池的充电过程包括恒流充电和恒压充电两部分,一般先进行恒流充电,再进行恒压充电,恒流过程是产生极化的过程,而恒压过程则是消除极化的过程,恒压过程时间越短,说明恒流过程产生的极化越小,电池性能越理想.最终选取平均内阻、开路电压、自放电率、充电容量、放电容量以及恒流充电时间占总充电时间的比值这6个指标作为电池的分选变量.其中,平均内阻取值为电池在1/3 C充满电和1/3 C放完电时内阻的平均值,记为R;开路电压取值为电池在1/3 C充满电3 d后的电压值,记为D;自放电率取值为电池在40 ℃条件下1/3 C充满电后间隔7 d的电压降,记为E;充放电容量分别取值为电池在1/3 C标准充放电条件下的充放电容量,分别记为Q1,Q2;恒流充电时间占总充电时间的比值取值为电池在1/3 C充电条件下的恒流充电时间占总充电时间的比值,记为B.
为了获取分选变量的测试数据,运用NEWARE充放电设备分别对100节电池进行充放电试验.其中,电池的充放电试验照片如图1所示.
2.2 分选变量的优化
为了消除分选变量之间的相关性对分选结果的影响,同时减少分选变量,简化计算,可以对电池的分选变量进行因子分析[9].
因子分析是一种统计学方法,其最常用的理论公式如式(1)所示:
统计学软件SPSS将相关系数矩阵、反映像相关矩阵、Bartlett球度检验以及KMO检验这4个统计量作为判断因子分析的条件.其中,经常采用的是Bartlett球度检验和KMO检验.
Bartlett球度检验通过判断相关矩阵来检验电池的分选变量是否适合做因子分析.Bartlett球度检验的原假设为相关矩阵是单位阵,只有拒绝该假设,因子分析才是有意义的,而要拒绝该假设就需要Bartlett球度统计量相应的概率值Sig小于给定的显著性水平;KMO检验是通过电池分选变量之间的相关系数来判断分选变量是否适合做因子分析.KMO值越大,则分选变量间的相关系数越大,它们的共同性就越多.通常,KMO值达到0.7以上就可以采用因子分析.
由于Bartlett球度检验和KMO检验都与分选变量间的相关矩阵有关,所以首先需要得到分选变量之间的相关矩阵.以选取的100节电池的6个分选变量的试验数据作为输入,经计算得到这6个分选变量的相关矩阵如表2所示.
由表2可知,电池的各分选变量之间具有较大的相关性,所以有必要对该相关矩阵进行Bartlett检验和KMO检验,得到的检验结果如表3所示.可见,Bartlett球度检验统计量相应的概率值Sig=0.000,小于给定的显著性水平0.050并且KMO=0.896>0.700满足因子分析条件,所以选取的分选变量可以通过因子分析来优化.
选择主成份分析法对选取的6个分选变量进行了因子分析,得到如表4所示的主成份的贡献率.主成份的贡献率表示的是经主成份分析法得到的各因子所能解释原分选变量的程度.
通常取特征值大于1的因子作为代表原变量的新变量[9].在表4中,有3个因子的特征值超过1,所以取这个因子作为新分选变量,即主因子F1,F2和F3.可见,分选变量经因子分析后提取3个主因子即可表达其86.834%的内容.
得到的因子矩阵如表5所示.
表5中的因子矩阵是每个原始分选变量在各因子上的因子载荷,比如,放电容量=0.970×F1-0.049×F2+0.094×F3.由表中的因子载荷可知,第一个因子主要表达的是放电容量、开路电压、充电容量以及恒流充电时间占总充电时间的比值这4个分选变量,第二个因子主要表达的是平均内阻和自放电率这两个分选变量,而第三个因子则比较综合地表达了各分选变量.
得到的因子得分系数矩阵如表6所示.
表6中每列的数据即是这3个主因子被原始分选变量表示的系数.比如:主因子F1=0.030×平均内阻-0.320×开路电压+0.012×自放电率+0.252×充电容量+0.320×放电容量+0.265×恒流充电时间占总充电时间的比值.
综上,最初的6个分选变量经因子分析后转化为3个变量(即3个主因子)就可表达原来分选变量的大部分信息,所以选取这3个主因子作为新的分选变量.另外,根据每个主因子能够表达原始分选变量的程度可将其综合为一个总因子,这个总因子的加权系数按照表4来确定,即总因子F=49.434%×F1+20.667%×F2+16.733%×F3.
2.3 电池的分选结果
聚类分析是直接比较各事物之间的性质,将性质相近的事物归为一类,性质差别较大的事物归入不同类的技术.
聚类分析中样本间距离以及样本与类、类与类之间距离的计算方法至关重要.鉴于平方欧氏距离度量的广泛应用,选取该距离作为样本间距离的衡量标准.该距离的表达式如式(2)所示.由于离差平方和法在实际应用中分类效果较好,应用较广,所以选取该方法来对电池进行聚类.
下面按照系统聚类的方法分别对电池样本进行主因子分选和总因子分选,并与传统分选法进行对比.另外,为了方便验证分选效果,在按照下面方法进行分选时,将所有的电池均分为4类.
1)传统分选法
传统分选法直接按照电池厂家传统的做法将放电容量、内阻和开路电压作为分选变量,即首先根据放电容量、内阻和开路电压进行电池单体的挑选,再按容量组内差、内阻组内差以及电压组内差进行分组,按照这种方法得到的分选结果如表7所示.
2)主因子分选法
主因子分选法是将3.2节中经因子分析后生成的3个主因子F1,F2,F3作为分选变量,运用SPSS软件中的系统聚类方法对电池进行聚类,其中,样本间距离的度量方式选用平方欧式距离,聚类方法选用离差平方和法.得到的分选法结果如表8所示.
3)总因子分选
总因子分选法是将总因子F作为分选变量,运用SPSS软件中的系统聚类对其进行聚类,其中,样本间距离的度量方式仍选用平方欧式距离,聚类方法仍选用离差平方和法.得到的分选结果如表9所示.
2.4 多参数分选效果对比
由于每节电池分选变量的初始数据是已知的,可以根据这些初始数据对分选出的各类电池进行评价,如表10所示,用各类电池的平均放电容量和平均自放电率来对此类电池性能进行评价.
由表10可知,传统分选法仅将内阻、开路电压和放电容量作为分选变量,并没有考虑自放电率等因素的影响,所以每一类电池的平均放电容量均相对较高,但是其平均自放电率也均较高,并且可能分布并不均匀;主因子分选法虽然考虑的因素较多,但是它并没有按照每个主因子对原分选变量的解释程度进行加权,分选出的每类电池的平均放电容量和平均自放电率均居中,而总因子分选考虑的因素较全面,并且按照每个主因子对原分选变量的解释程度进行了加权,所以由其分选出的每类电池的平均放电容量均较高,平均自放电率均较低,并且类与类之间差别较大,其分选效果最好.
3 动态特性分选
多参数分选法是静态分选,虽然能反映出动力电池的某些特性,但主要是外部特征,也无法反映出充放电过程中电池特性的变化趋势;动态特性分选法以放电曲线为依据,考虑了电池在充放电过程中其内部结构的不同,结合多参数分选,能够挑选出一致性较好的电池,从而提高电池组的性能.
3.1 电池充放电曲线的离散拟合
由多参数分选结果试验对比可知,总因子分选法在3种多参数分选方法中是最好的,但是由于分选出的第Ⅲ类电池性能相对较差,第Ⅳ类电池仅有1节,所以只能在第Ⅰ类(29节)和第Ⅱ类(53节)电池的基础上再进行动态特性分选.
在电池充放电曲线上选取p个采样点,则电池的充放电曲线可以转化为一个一维特征向量.对于一组待分类的n节电池,可以将一簇充放电曲线转化为一个n×p维的原始数据阵.
电池之间性能的不同会导致电池的充放电时间不同.为了使代表每节电池的特征向量长度相同,便于计算电池之间的距离,需要对每节电池的充放电数据进行拟合,这里仅对搁置和放电部分进行,得到了代表每节电池的100个搁置数据点和500个放电数据点,共600个数据点来代表一节电池.
3.2 电池的动态特性分选
对电池的动态特性分选需要确定聚类方法,本文根据电池的充放电曲线采用模糊C均值聚类算法来对电池进行分选.
模糊C均值聚类算法是Jim Bezdek博士在1973年提出的一种基于目标函数的聚类算法[10].下面对它的隶属度函数、相似性函数以及目标函数进行简单的介绍.
1)隶属度函数
隶属度函数用于表示一节电池属于某一类电池的程度,用uA(X)表示,如果它的值是1,则说明这节电池完全属于某一类电池.由归一化规定知,一个数据集的隶属度的和总等于1,即如果有n个样本,c个聚类中心,则
2)相似性函数
选取平方欧氏距离作为相似性函数,此距离越小,说明两个样本越相似.
3)目标函数
这两个必要条件使得模糊C均值聚类算法成为一个迭代过程.此过程具体如下:首先,需要初始化U,并且使其满足求和为1;其次,用式(8)计算c个ci;最后根据式(6)计算目标函数,如果满足条件,则算法停止,如果不满足条件,则用式(9)计算新的U,再从头开始计算.
根据模糊C均值聚类算法的介绍,在总因子分选法的基础上将n节电池样本聚成c类.为了方便验证,以最终挑选出的电池节数m=4为例,其算法流程如图2所示.
按照图2所示的流程,运用MATLAB编程实现该算法,从而得到运用动态特性分选方法分选的结果.
以第Ⅰ类电池(29节)为例,由于电池节数较多,所以先将其分为3类,再针对每一类进行模糊C均值聚类,得到的聚类结果如图3所示.目标函数J迭代了13次就达到了1e-5,满足设定条件,迭代停止.
由图3可知,29节电池中的第2类仅包含2节电池,可将其舍掉,第1类和第3类分别包含13和14节电池,可以继续对其分别再进行聚类.
1)13节电池的聚类结果:
当聚为3类时,得到如图4所示的聚类结果.
当聚为4类时,得到如图5所示的聚类结果.
由图4和图5知,无论聚为3类还是4类,61,78,80,87这4节电池始终聚为一类,所以可以认为这4节电池的一致性较好.
2)14节电池的聚类结果:
当聚为3类时,得到如图6所示的聚类结果.
当聚为4类时,得到如图7所示的聚类结果.
由图6和图7可知,聚为4类时的第1类电池(6节)均包含在聚为3类时的第1类电池(8节)中.为了挑选出一致性较高的4节电池,对聚为4类时的第1类电池继续进行聚类.
对于这6节电池,当聚类数为3时,得到如图8所示的聚类结果.由图4,图8可知,每一类电池数均小于4节,而本文最终聚类的电池数统一为4节,所以认为聚类数为3时是不合理的.
当聚为2类时,得到如图9所示的聚类结果.可见,10,15,28,90这4节电池聚为一类.所以这14节电池中,10,15,28,90这4节电池的一致性较好.
由上面聚类过程可知,在这29节电池中,61,78,80,87和10,15,28,90这两组电池一致性较好.

