第二讲试验研究中的优选法简介和讨论
徐静安
技术讲坛
第二讲试验研究中的优选法简介和讨论
徐静安
优选法涵盖领域广泛,包括优化试验、优化计算、优化设计、优化控制等,本文侧重优化试验讨论。将试验研究对象看作一个总体,根据已有条件和需求,可以进行机理性、经验性、统计性研究。本文着重于统计性实验研究。直白地表述:在研究对象的总体范围内,选择少量有代表性的实验点样本,对总体的响应最优值(较优值)及其规律统计模型作出有效的推断预报。如何选择实验样本点构成实验方案,就是优化试验方法的内容。
优化试验方法一般分为两大类:间接分析法和直接分析法。间接分析法就是预先设计实验方案,进行多个样本点实验,用回归分析等数据处理方法,构造一类函数来逼近这些实验值,再用优化方法计算函数极值,进行统计分析并通过实验进行验证。直接优化法是在初始实验基础上按一定模式(规则),根据前面实验点的结果,比较分析推算优化方向和下一个实验点,而不求出具体的统计模型。该方法是逐步逼近最优点的方法,又称“循序试验法”、“序贯试验法”,在最优化理论中颇受重视,可处理没有数值解析的表达式,也可以求复杂函数的最优解。
一般来说,实验室小试、模式由于实验条件处于专业可控范围内,考察的变量因素范围可适当宽泛,所以都采用间接分析法。而对于中试、示范装置、工程化装置,一则研究对象复杂,二则为避免恶劣工艺条件组合产生安全技术风险,可从可用的初始条件起步,按一定模式进行小步长序贯寻优试验。
一单因素优化试验
(中点)平分法适用于单调函数。美国Kiefer于1953年提出的黄金分割法(0.618法)及分数法仅适用于单峰函数。分数法利用菲波那契数列,类同于0.618法进行操作。该类方法后一个实验点的安排需依赖前面实验结果的对比,然后顺序进行。
在实际实验研究时,要求对研究对象的内在规律——函数特性作出先验判断。所以在难以判断对象特性时,大都在实验范围内按等步长安排实验点。
需要强调的是,利用单因素试验考察的实验点(或称水平数)L≥5时,用二次多项式、三次多项式进行拟合,可得近似最优点。
二拉丁方设计
在生物学试验中,涉及到环境条件(光照、温度、水分、通风、营养等)中难以严格控制的非变量因素,如田间试验土壤基础肥力的差异等。为了降低试验误差,与一般的理化实验不同,在随机、重复的基础上增加“局部控制”的“区组”,使考察处理的外部环境更为接近。按这样的概念构成的试验方案中行数、列数二者相等,该正方形试验方案又用拉丁字母表示,故称为拉丁方设计,具体应用时可查拉丁方设计表。表1所示为考察三个变量因素A、B、C的3×3拉丁方的具体方案。任意两个因素的不同水平各搭配一次,比较均衡。
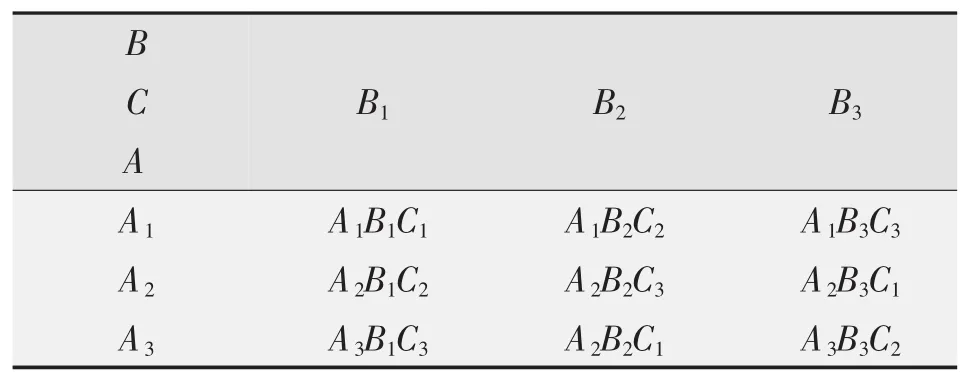
表1 3×3拉丁方设计方案
实验样本量是行或列水平数的平方,即N=L2,所以拉丁方设计考察的变量及其水平数不能太多;拉丁方设计采用方差分析处理数据,样本量也不能太少,否则会因误差自由度过小而影响实验结果检验的灵敏度。
拉丁方区组因素的试验设计是最古老的试验设计方法,由英国人Fisher R A于20世纪30年代提出,是由理论研究驱动的技术创新。拉丁方设计广泛应用于农业田间试验,并由此开创了试验设计这一新的领域,具有里程碑式的意义。
三 多因素降维法
实际研究对象影响目标响应值大都是多个变量因素。在试验方法中,多因素问题带来的复杂性是变量因素间的交互作用和多维空间函数的多峰性。降维法是将多维问题进行简化的方法,其中坐标(因素)轮换法是应用较广泛的方法。对其他变量先赋值,降维至一维,进行单因素考察,找到好点,“从好点出发”依次轮换坐标进行单因素考察。
图1为研究对象的等高线图,考察因素A、B各包括6个水平,这在系统研究前是未知的。进行降维单因素考察时,假定先赋值A3,对B进行考察,A3B4为好点;固定B4轮换考察A,结果A3B4仍为好点,则得出Y=7,完成一轮降维法单因素考察。
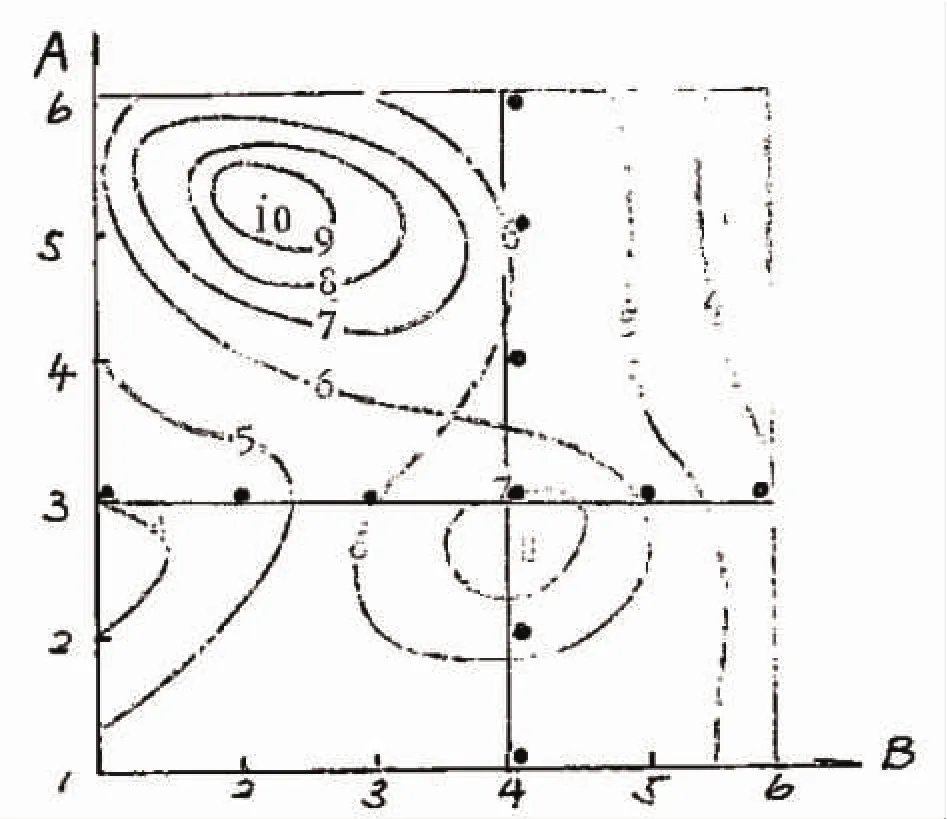
图1 高等线图
若考察变量数为M,其水平数为L,则全面组合试验次数N=LM,降维法考察一轮实验点的次数N'=M*L。但是,供选择的降维方案有n=L(M-1)种,不同方案得到的结果是不同的。
该方法简单明了,符合一般的思维习惯,每个因素对目标响应值Y的影响均具有可解释性,因此应用广泛。但是对于多维复杂问题,利用一轮降维单因素考察法尽管也可得到“好点”,却无法考察变量因素间的交互作用,易落入局部优化的陷阱。图1直观地显示了方法的局限性,如果随机地采用一轮降维单因素考察结果来描述研究对象是存在技术风险的。显然,不同的降维方案(即对A不同的赋值)会产生不同的结果。目前该方法大都用于研发工作前期的探索试验,为主体优化试验作技术准备。
四 多因素模式法
模式法就是按照规定的一些模式进行实验,比对计算后寻得优化方向,探索前进。在诸多模式法中,正规单纯形模式法较有代表性。
单纯形概念由美国数学家丹齐克G B于1947年提出,单纯形优化法由Spendly于1962年提出。单纯形是指多维空间的一种凸图形,在几何构图时所需顶点数最少。二维正规单纯形为正三角形,三维的为正四面体,即其顶点数是图形的维数加1。高维的图形无法几何描述,而在笛卡尔直角坐标系中顶点坐标可用代数方法表述。
图2为正规单纯形模式方法图解。选定步长a,以正三角形的三角顶点P0,P1,P2为起始实验点,比较结果表明P0为最差点。按“差点的对称点为好点的方向”的原则,求得P3点,构成P1,P2,P3组成的新单纯形,以此类推,序贯进行,直到找到满意的结果。
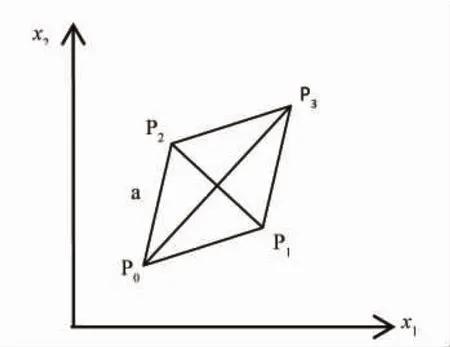
图2 正规单纯形模式法
该方法概念清晰,在多维空间坐标中顶点的坐标值可通过计算公式获得。适合大规模生产装置的工艺优化,从现有工艺条件P0出发,控制步长a不致于引起工艺条件的过大波动,逐步寻优。模式法中还包括直角单纯形法、矩形调优法及步长加速法等。
1978~1979年,笔者在化工部兰州化工机械研究院工作期间,参与广州氮肥厂重油气化攻关工作时,与上海化工研究院的同仁合作,在气化炉的工艺调优中曾学习、探索过该方法。由于现场控制仪表的精度不够,导致P点值的波动过大而影响判断结果。
对于多峰函数,该方法仍有可能落入局部优化的陷阱。
五 多因素随机法
根据优选概率,对多因素考察范围随机选点,形成样本量为N的实验方案,对N个实验结果直接对比,达到优选的目的。
图3为两个变量因素的随机点方案。对变量考察范围,按实验可能的控制精度,等步长地划分网格,再用随机数形成实验方案。根据期望获得的“好点”概率,可以计算出需要的实验点样本量N。

图3 统计实验法方案
该方法对目标函数没有过多要求,可以是单峰,也可以是多峰,在多因素时具有相对优势。随机试验法在文献中被称为蒙特卡洛法,于20世纪40年代由乌拉姆与冯·诺依曼提出,可将复杂对象的分析问题转化为统计模拟问题。
由于试验设计的发展,用数论方法找到的伪随机数比蒙特卡洛法中的随机数更均匀,所以不作进一步介绍。但在多因素随机法中,随机调优法可用于目标函数复杂、变量因素不限的优化问题,且因素越多该方法越有优势,应予以关注。
随机数的产生可借助MATLAB软件中的Rand函数。在实验研究统计模型预报功能时,可调用Rand函数在考察范围内产生随机化的验证点集。
六 序贯设计法
在试验设计方法中,除了广义的“序贯试验法”外,另辟专门的序贯设计法。此法的特点是在研究决策问题(统计推断或选择)时,不预先固定实验样本量,而是逐次取样安排实验,直到样本提供足够的信息,能正确作出决策为止。也就是说实验方案的样本量是随机的,逐点利用前次获得的信息决定下次的实验,样本是一个一个逐次得到的序贯样本。
1947年,Wald A的奠基性著作《Sequetial analysis》出版以来,序贯分析研究广泛,被认为是对统计学发展史的重大贡献。
序贯法有两个要素:停止法则与判别法则。停止法则告诉我们在对总体进行逐次抽样实验过程中何时停止;判别法则根据停止时得到的序贯样本实验数据,对总体作出推断或选择(接受或拒绝一个假设、估计参数等)。
早在1943~1945年,Wald A在序贯分析中提出序贯概率比检验SPRT,为适应美国二次大战中军火生产的质量控制,对经典检验进行了重大改进。经典检验是:某统计量>临界值,拒绝假设;某统计量<临界值,接受假设。改进的基本思想是当统计量不太大也不太小时,不急于下结论,而再抽样实验一次,采用序贯样本的方法,直到统计量足以下结论为止。推而广之,当同时检验几个统计量,部分统计量不大不小而不能全部通过时,亦可采用该方法。计算结果证明,在相同的犯错误概率α下,相对于固定样本量方案,SPRT所需平均序贯样本量最小,即效率较高。
对实验研究可能的竞争性模型(理论模型、经验模型、统计模型)进行筛选,是我们感兴趣的问题。序贯设计过程为:(1)根据模型待定参数先在考察范围内随机进行相应实验点(待定参数个数+1)的初始预实验,求得模型初始参数;(2)用最优化方法求判别式Δmax时的下一个实验点;(3)实验并得到响应值Y进行判别,依此进行序贯分析直到满足预定的精度。
笔者认为可对序贯设计法的选优思路作进一步引申和改进,将初始预实验的随机点集改为更有效率的较小样本量的均匀设计(创立序贯法时尚无均匀设计),求得模型参数及相应统计量;由于样本量较小及实验误差等的影响,模型预报精度及统计量不能满足时,引入SPRT概念,再行抽样进行下一个实验(对模型进行学习、修整),直到满足预定的精度,作相应的统计推断并进行验证。探索驱动了新方法的萌芽。从理论上分析,先验地安排固定的较大样本量时存在实验点富余的可能性。把均匀设计和序贯分析相耦合的设计方法效率更高,姑且称之为序贯均匀设计方法,笔者和同仁已在多个项目中成功应用。
七 正交试验设计
二次大战后,拉丁方设计基本技术引入日本,以田口玄一教授为首的研究人员于1949年起开发了各种正交试验设计,1957年进一步开发了信噪比S/N设计和三次设计等,这些设计方法成为质量管理的重要工具,是当年日本“质量立国”战略的技术基础,也是试验设计领域发展的第二座里程碑。正交实验设计是由市场驱动的创新。
正交试验设计是利用数理统计学观点,应用正交性原理,在研究考察范围内选择一定样本量的具有代表性的实验点,构成正交表的一种设计方法。
图4为M=3,三个因素A,B,C的水平L=3的正交试验实验点分布。全面组合实验次数N=LM=27,正交试验次数N=L2=9,均为具有代表性的实验点。选用L9(34)正交表(见表2)。在考察范围内实验点布点均匀能获得更多信息,每两个因素之间是L2的全面组合试验。
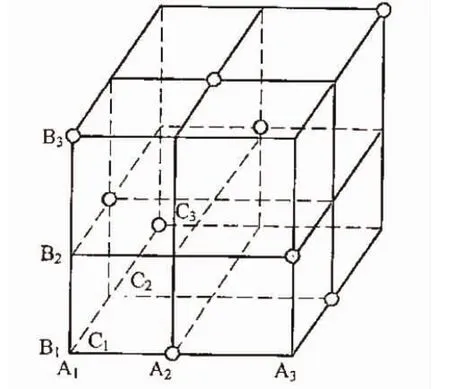
图4 正交试验试验点分布
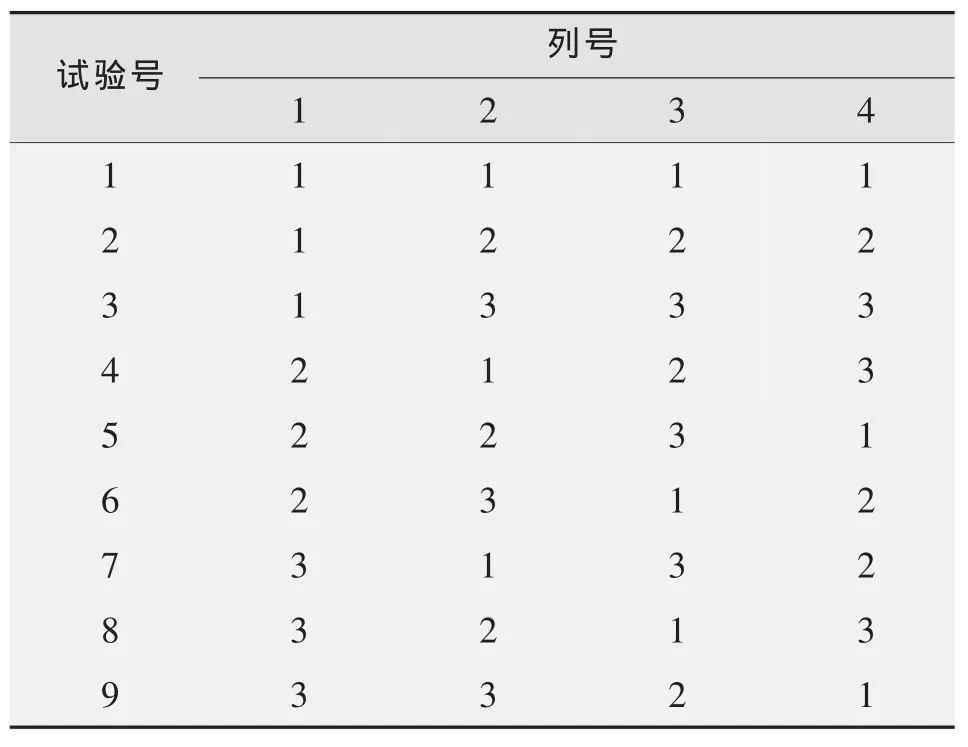
表2 L9(34)表的具体方案
正交试验设计具有“均衡分散、整齐可比”的特点,可以得到优化的ABC组合条件。表格化的设计方案、程序化的方差分析、直观化的结果显示,受到不同专业研究人员的欢迎。
表2是L9(34)表的具体方案,A,B,C分别安排在1,2,3列。每张正交表都有相对应的两列间交互作用表,供使用时进一步的表头设计。L9(34)表为考察4个变量因素、3水平的试验设计表,使用该表时存在交互作用和主效应间的混杂现象。
从表3可见,L9(34)表安排2个因素,交互作用不混杂,但此时A,B是全组合试验,没有正交试验的特色;安排3个因素可节省实验工作量,但交互作用对主效应A,B,C部分混杂;安排4个因素可大大节省实验量,但交互作用全面混杂。概括地说,如有先验的经验判断或者抓主要矛盾(即仅求取较优工艺条件),则那些交互作用可以忽略。正交试验设计正是忽略了交互作用的考察,才“节省”了实验次数,这是正交设计的不足。

表3 L9(34)表安排不同因素数的具体方案
此外,正交设计样本量N=L2甚至更大,对于变量考察范围较大,水平数大于5的多水平场合,实验量较大。而硬性地将水平数压缩为2,3时,用大步长离散网格来筛选优化点,存在较优条件漏网的风险。
由此可见,正交试验设计比较适用于多因素、小范围且对因素间交互作用有所了解的研究对象,尤其是从现有工艺出发,进行小范围调优及质量控制研究具有相对优势。
笔者在兰州化工部化工机械研究院工作期间,于1980年7月、1988年8月以《正交试验法》为教材,于1984年7月以《技术数理统计方法》为教材,三次举办培训班主讲并推广正交试验法。正交设计法还包括正交表并列设计(混合水平)、拟因子设计、部分追加法、裂区法等。鉴于当前已有更为先进的均匀设计法,不再进一步展开。
八 回归正交试验设计
上述正交试验设计通过极差分析、方差分析得到较优的条件组合,但不能通过统计模型对离散水平之间可能的优化组合作出可靠的预报和对交互作用进行全面考察。数理统计求取统计模型一般应用最小二乘原理,利用回归分析建立变量和响应的统计方程。回归分析和正交试验设计是互相独立的应用数学分支,但二者耦合构成回归正交试验设计。解决局限、不足驱动了新的方法产生。
回归正交设计在二水平正交试验点基础上,扩充增加星号试验点和零号试验点,构成试验设计方案。试验点分布见图5、图6,变量因素水平需增添为L=5,增加了实验样本量。如前述三因素案例,构筑三元二次回归正交设计的方案实验次数N=15。

图5 二元二次回归正交组合设计试验点分布
由于当年计算机及回归分析软件还不普及,回归正交设计利用正交性、通过编码转换,不需要进行矩阵转置、求逆运算,仅依靠计算器进行表格式的运算即可求得经典的全回归模型,一度受到关注。
笔者认为回归正交试验设计现已失去优势。从试验设计的角度分析,既然研究对象允许变量水平扩充为多水平(L=5),均匀设计的效率更高;从数据处理的角度分析,软件化的逐步回归已取代经典的全回归分析。
由于近年出版的不少教材仍有关于回归正交试验设计的章节,所以本文也单独对其进行讨论,读者仅作科普性了解即可。

图6 三元二次回归正交组合设计试验点分布
九 因子设计
因子设计是一种多因子(变量因素)试验设计方法,经方差分析可以量化各因子及其交互作用对Y响应的效应。该方法主要用于对大量因子(M>5)进行研究的初期探索阶段,即进行因子筛选。
在一项新领域的研究工作中,科研人员的先验经验不足,需要考察的因素量M可能很多,但最终可能只有少数因素对响应值Y有实际影响(效应稀疏性)。利用因子设计法经初期因子筛选后,对保留的因子可以进行更为细微的主体优化设计试验。但是,因子设计实际上是个全组合实验方案,包括2M、3M因子设计,将研究因子范围粗定为2水平、3水平,2水平为线性简化。假定考察M=3,因子水平L=3,分别为0,1,2。如图7所示33因子设计布点,该设计实际上是N=33=27的全组合实验。如果M=5,L=3,则N=35=243,仅仅是初期的筛选试验,就有这样大的实验工作量。所以多因子筛选逻辑上的合理性和实验上的可操作性有很大矛盾。
笔者认为因子设计是试验设计技术发展过程中曾经出现过的一种方法,与当前的均匀设计和逐步回归设计技术相比,已无特色、优势,仅作浏览即可。

图7 33设计的处理组合
十响应曲面法
英国统计学家Box G和Wilso于1951年提出响应曲面法(RSM),随着计算机数据处理技术的发展,能给出2个变量对响应Y的图形。便于直观判别优化区域的RSM,一度得到了关注。
当多因素试验在初期筛选因子后,只留下为数不多的因子(M=2~4),并搜索到优化区域,再采用RSM进行实验、建模和数据图形处理。一阶响应曲面是作了线性简化,二阶响应曲面为了二次多项式拟合建模需要,对实验方案及实验点作了与回归正交试验设计相类似的技术处理,将变量水平扩展为L=5,见图5、图6。
笔者认为,凡是能统计建模的试验设计,加上图8所示计算机作图(响应曲面、等高线图)功能,均可达到RSM的效果。

图8 二因素的三维响应曲面
一阶、二阶响应曲面法,包括1960年推出的二阶响应曲面的改进Box-Behnken设计,在当今试验设计中并无系统的优势。
至于建模后图形处理和显示,现有MINITAB等软件均有较强的功能模块给予支持。
十一 均匀设计
1978年王元、方开泰用数论方法(或称伪蒙特卡洛法)开发出了均匀设计。该方法被成功应用于多因素多水平的导弹设计问题,并获得推广应用。均匀设计被国际数理统计界公认为先进的试验设计方法,是一种稳健设计方法,也是用于大系统计算机仿真试验设计的重要方法之一[国外还有“拉丁超立方体抽样(LHS)”方法]。
正交设计的特点:“均衡(匀)分散”使实验点具有代表性;“整齐可比”使实验数据可以直观进行比对分析。为了保证“整齐可比”,正交设计的两个因素间必须全面进行组合实验,即最低实验次数N=L2。而均匀设计在实验考察范围内只考虑均匀分布,数据处理依靠回归分析(逐步回归),所以实验点可进一步降低,每个水平只做一次实验,样本N=L,实验设计方案效率更高;回归分析也有助于对变量间的交互作用作深入考察。
对均匀设计的样本量,数据处理系统(DPS)建议N=3M,笔者推荐N=(2~2.5)M,可根据研究对象的复杂程度及实验误差的控制水平选用均匀设计表。
表4 表及其配套的使用表
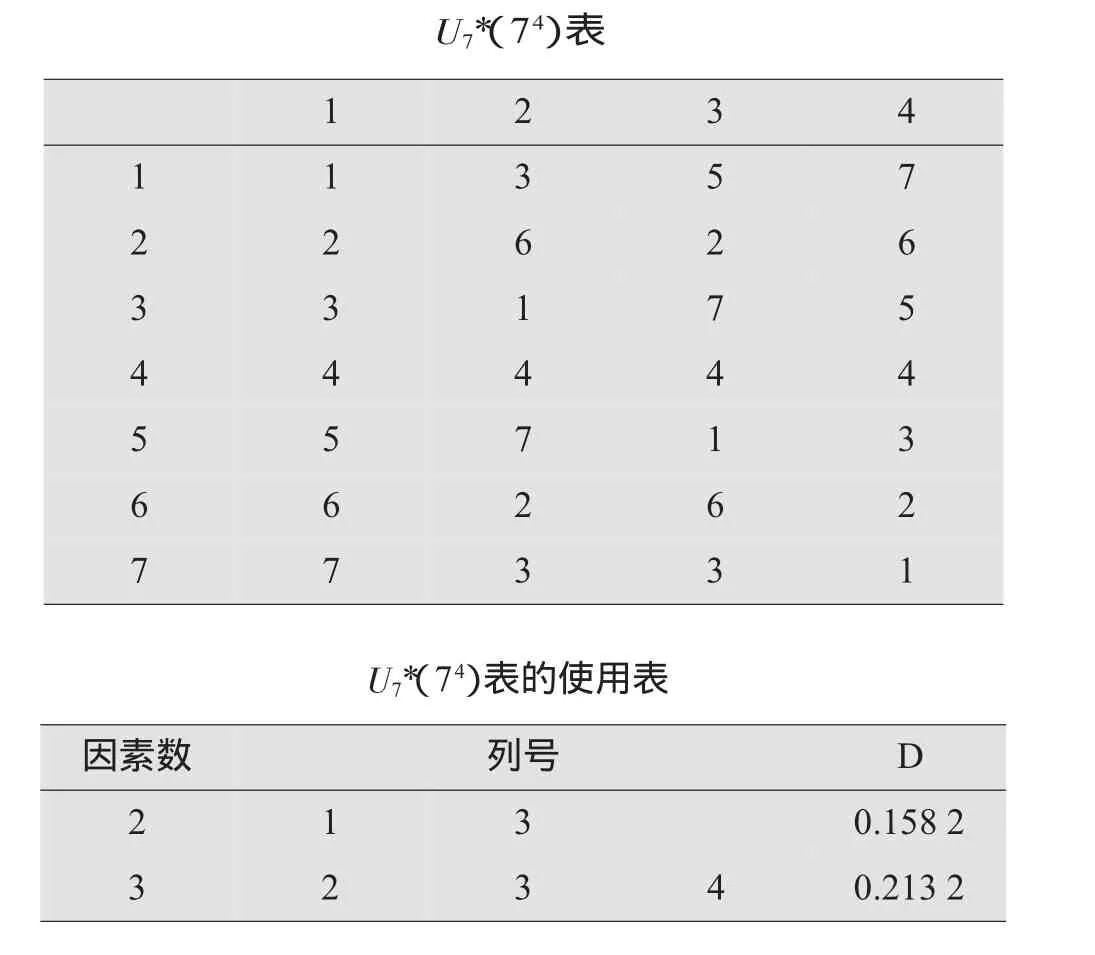
表4 表及其配套的使用表
U7*(74)表1 2 3 4 1 1 3 5 7 2 2 6 2 6 3 3 1 7 5 4 4 4 4 4 5 5 7 1 3 6 6 2 6 2 7 7 3 3 1 U7*(74)表的使用表因素数列号D 2 1 3 0.158 2 3 2 3 40.213 2
若以本文在不同试验设计中列举的因素M=3、水平L=5为例,进行设计方案分析,则
全面组合实验次数N=LM=53=125;
降维单因素考察一轮实验次数N=L×M=5× 3=15,忽略交互作用,陷入局部优化;
正交设计实验次数N=L2=52=25,选用L25(56)正交表,忽略交互作用,效应混杂;
正交回归设计实验次数N=15,选用三元二次回归正交设计;
均匀设计在多因素多水平研究问题中,显示出突出的优势。
20世纪80年代,导弹设计中有个项目是5个变量(M=5),试验水平数不少于10(L≥10),而实验总次数又不能超过50(N≤50)。这是一个多因素多水平的研究对象,由于无法采用正交设计及其他试验设计方法,研究工作面临困境。
王元、方开泰于1978年受当时的第七机械工业部委托,用数论方法开发出了新的均匀设计,实验量N=31,取得了成功。这是由需求驱动的创新。
20世纪90年代中后期,笔者曾支持院科研处外请专家来院讲授均匀设计,教材是方开泰著的《均匀设计与均匀设计表》,该书我保留至今,时常翻阅。多年来也努力应用并推广均匀设计。30多年来,均匀设计从军工系统向民用系统扩散、转移,得到迅速发展和应用。均匀设计方法受到普遍关注。随着试验设计和数据处理技术的发展,均匀设计还包含有定性因素的均匀设计、混料均匀设计、均匀序贯设计,以及均匀设计和其他数值计算技术的耦合优化,如UD+Fluet、UD+ASPEN等。均匀设计作为当代优化试验设计的主流技术,值得学习、应用、推广。
十二 混料(配方)设计
在科学研究、工农业生产中,混料——配方问题是广泛涉及的研究对象。混料试验中分量组分至少有三种(p≥3),每个组分χi的质量分数总和等于1,即

实验响应值Y仅与xi的占比有关,而与其总量无关。由于Σχi=1约束条件的存在,和以往试验不同,变量因素——组分xi是不独立的,所以试验研究的设计方法、数据处理技术均有根本性的差异,因此试验设计就包括专门的混料设计。
在混料设计中,要以单形坐标系而不是笛卡尔直角坐标系来进行描述。单形是指顶点数与坐标空间维数相等的凸图形,一般采用正单形,如正三角形、正四面体等。P维单形即P-1单纯形,P=3即高为100%(1)的平面正三角形,构成三线坐标图。正三角形内任意一点R(具体的实验点)都有三个组成的含量坐标,且x1+x2+x3=1,如图9、图10所示。P=4为正四面体,P≥5时无直观图形,用数学描述。
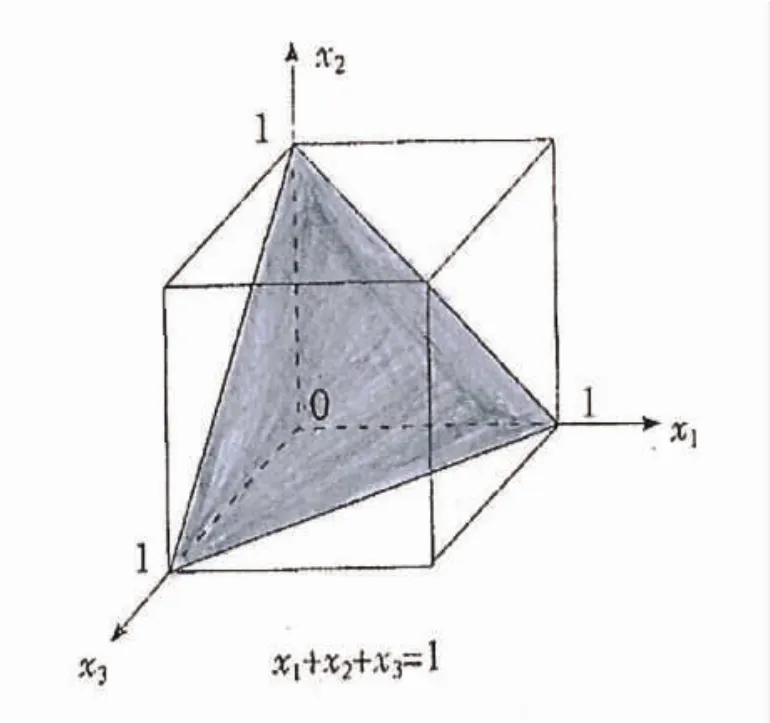
图9 混料设计约束图
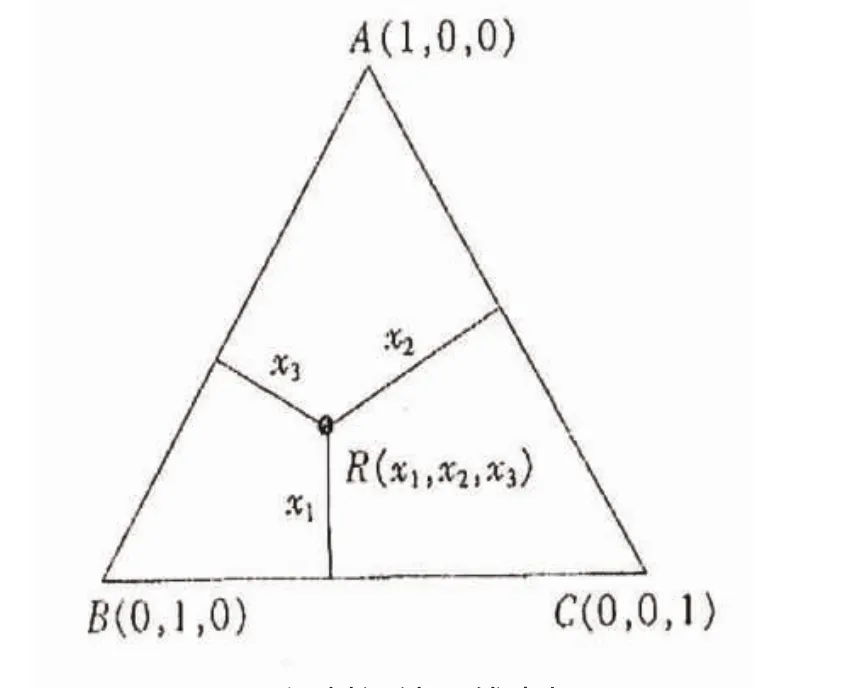
图10 混料设计三线坐标图
Scheffe于1958年在正单形坐标体系基础上提出单纯形格子点法,1963年提出单纯形质心法。Cormell提出了轴设计法,并在1990年对经典的混料设计作了综合介绍。MINITAB软件有相应模块支持单纯形质心法、单纯形格点法、极端顶点设计法,只要输入实验条件计算机即可生成混料设计方案。

图11 单纯形设计图
图11为利用极端顶点设计法分析某个阻燃剂案例的实验点分布。
在经典混料设计法应用过程中,发现了新的问题:(1)实验布点局部密集,点集TP布点不均匀;(2)界面点过多,在无下限约束中,实验时某个组分为零,造成化学反应不发生或生成另一种产物,非实验所求。问题驱动创新,王元、方开泰在1978年提出的均匀设计基础上,于1990年提出混料均匀设计,2000年完善为条件分布法的混料均匀设计。DPS软件中有相应模块支持混料均匀设计。
表5为无上下限约束的P=5的混料均匀设计表,实验点组分没有零值,布点更均匀。

表5 无上下限约束的P=5的混料均匀设计表
本文对讲座涉及的试验设计方法等作概括介绍,对主要的现代技术,今后将专题作应用性介绍。
最近笔者阅读了《中国人才》(2015年11期),国外知名职业人士社交网站Linkedin对全球超过3.3亿用户的工作经历和技能进行了大数据分析,公布了2014年最受雇主喜欢、最炙手可热的25项技能,其中“统计分析和数据挖掘”技能位列榜首。具体到人是“具备IT技术能力、数据统计能力以及本专业过硬的复合型人才”。
脚踏实地、眼望星空。愿青年科研人员结合岗位工作,学习、应用数理统计方法、数字化技术,提高研发水平和技术创新能力。
(略)

