城市轨道交通线网时空相关性客流预测研究*
邹 东刘 琼黄梓荣
(1.广州地铁集团有限公司建设事业总部,510380,广州;2.华南理工大学软件学院,510006,广州∥第一作者,高级工程师)
城市轨道交通线网时空相关性客流预测研究*
邹 东1刘 琼1黄梓荣2
(1.广州地铁集团有限公司建设事业总部,510380,广州;2.华南理工大学软件学院,510006,广州∥第一作者,高级工程师)
城市轨道交通客流预测是一个时空相关的复杂问题,仅根据车站的历史数据很难得出更有参考价值的预测结果。提出基于Elman神经网络算法的时空相关性客流预测方式。其模型输入包括车站的历史数据和线网中其它车站及交叉线路车站的时空相关性数据。前者从车站前3周数据中提取纵向强时间相关性数据;后者从相关车站的前3周数据中提取横向强时间相关性数据。提取过程均采用Spearman算法。在两条交叉线路共33个车站3周时间范围的客流数据上,利用Elman神经网络算法比较分析时空预测方式和时间预测方式的预测性能。试验结果表明,时空预测方式对实际客流的预测精度优于时间预测方式。最后,在时空预测的基础上进行客流多步预测,为城城市轨道交通有效的客流疏导提供数据支持和相对宽裕的时间。
城市轨道交通线网;相关性分析;客流预测;神经网络
First-author's address Operation Division of Guangzhou Metro Group Co.,Ltd.,510380,Guangzhou,China
近年来,城市化进程不断加快,城市轨道交通线路持续增加,建立与时俱进的轨道交通管理方案迫在眉睫[1]。城市轨道交通线网建设是协调线路运力、综合节能、提供应急指挥等的重要举措。目前,城市轨道交通线路独立运营,其列车未能按客流波动调度,高峰拥挤、平峰浪费的运营问题十分突出。运营方应分析客流变化趋势及其影响因素,建立相适应的客流预测模型,准确预测线网站点的客流,促成各线路客流量均衡分布,以满足市民出行需求。
客流的时变性是城市轨道交通的特征之一,相对于线路站点的客流,线网站点客流的时空分布将发生显著变化。由于线网包含多条线路,其站点间关系复杂,且车站用地类型各异,客流关联规则未知,已有数据缺乏部分重要信息(如天气、车站周边交通情况、社会经济文化情况等),因此,准确预测站点客流的时空变化趋势是一项具有挑战性的任 务[2]。
目前,国内外学者对交通领域的客流预测方法进行大量的研究,但是大部分研究都基于交通理论。文献[3]提出客流预测的DRM模型,并对加州旧金山轻轨车站客流进行分析预测。文献[4]基于DRM模型进一步研究了首尔的城市轨道交通车站客流量。文献[5]利用希尔伯特-黄转换方法对台北捷运的客流数据进行预测分析,该方法充分考虑了轨道交通客流的时变特征,能有效解决客流数据的非线性、复杂性问题。文献[6]考虑大型活动对城市轨道交通客流的影响,对北京地铁五棵松车站的客流使用灰色马尔科夫进行分类预测。文献[7]利用路网的空间信息,提出了一种基于时空依赖性的区域路网短时客流预测模型。
线网的客流错综复杂,线路、车站之间相互影响,但已有的客流预测方法大部分基于单车站的客流,对该车站的历史客流数据进行研究,忽略网络化运营情况下线网车站的相互影响,导致在进行客流预测时忽视空间相关性,降低了预测结果的拟合精度。
时空相关性客流预测模型从城市轨道交通网络化运营的角度考虑线网车站的客流预测问题。该模型的输入由两部分组成:①当前车站的历史数据;②其它相关车站的时空数据。模型输出即为所预测的客流量。
利用Spearman算法分析预测站点客流数据的时间相关性时,可提取相关性较大时段的数据作为历史数据。采用两层的时空数据构建方法:①利用Spearman算法,分析预测站点与本线路其它站点、预测站点与交叉线路站点的空间相关性;②提取与当前车站空间相关性较高的车站,计算时间相关性;③提取相关性较高的时间段数据作为时空数据。得到模型输入后,建立Elman神经网络的预测模型,并使用该模型对城市轨道交通线网的车站客流进行预测。
1 客流数据特点
城市轨道交通客流量指在单位时间内城市轨道交通线路上的各旅客流向的流动人数的总和。城市轨道交通的客流具有一定的时序特征,即客流量会随着时间的变化而变化。其中,最明显的是客流量以周为变化周期。同时,客流量还会受到其它因素的影响。这导致每个周期内客流量的变化不尽相同,具有一定的非平衡趋势特征。
城市轨道交通的线路固定,并与其它交通方式相互分离,故较少受到外界因素的干扰,其客流量随着时间不断变化。为了反映客流量的这种变化情况,得到准确的预测结果。在进行客流量预测前,应首先掌握客流量的时序特征及变化趋势[8]。以广州地铁2号线三元里站为例,其某年的客流量变化情况如图1所示。通过对图1进行分析可发现,三元里站的客流量具有如下特征:
(1)周间特征。在不考虑节假日客流的情况下,客流量以周为周期。每个周期内的客流变化规律相似。
(2)周内特征。一般情况下,每周五的客流量最大,是一周客流量的最高峰;其它工作日的客流量相对较为平均;而周末的客流量最小,为该周低谷。
(3)日内特征。根据车站周围用地类型的不同,其客流量在一天内的变化特征各不相同。商业用地附近的车站客流量,在工作日有明显的早高峰和晚高峰特点。
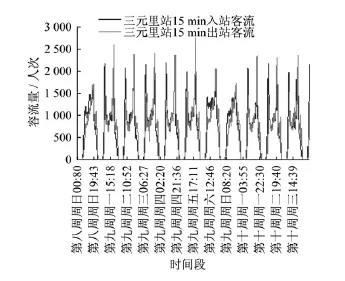
图1 广州地铁三元里站分时客流量
2 基本原理
2.1向量相关系数
在确定Elman神经网络的输入、输出向量时,需考虑各输入向量与输出向量之间的相关系数,以确定输入向量与输出向量是否相关,从而确定是否能够从输入向量的变化反映出输出向量的变化。
常见的相关系数有pearson相关系数、Gamma相关系数、Kendall's Tau-b相关系数、Spearman相关系数等。
假设Spearman相关系数的两个集合分别为X、Y,其元素个数均为N,两个随机变量取的第i(1≤i≤N)个值分别用xi、yi表示。对X、Y进行排序(同时为升序或降序),得到两个元素排行集合XORD、YORD,其中元素xord,i、yord,i分别为xi在XORD中的排行以及yi在YORD中的排行。将集合X、Y中的元素对应相减得到一个排行差分集合d,其中di=xord,i-yord,i,1≤i≤N。随机变量X、Y之间的斯皮尔曼等级相关系数ρ可由xord,i、yord,i或者d计算得到。其计算式为
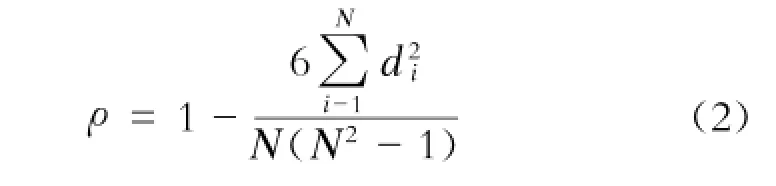
2.2Elman神经网络
Elman神经网络是一种典型的动态神经网络。Elman神经网络在前馈网络的隐含层添加一个承接层以实现记忆功能,从而使其能反映数据的动态特性。
Elman神经网络一般分为输入层、隐含层、承接层和输出层,其一般结构如图2所示[9]。
假设u(k)及y(k)分别为Elman网络输入值及输出值,x(k)为隐含层的输出值,xc(k)为承接层的输出值,那么Elman神经网络的数学表达为:
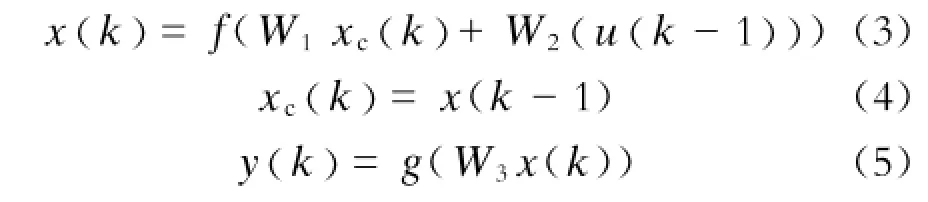
式中:
W1——承接层神经单元到隐含层神经单元的连接权重矩阵;
W2——输入层神经单元到隐含层神经单元的连接权重矩阵;
图6为满载下的实验波形,图6中,vgs、vds分别为LLC原边管子的驱动电压和漏源电压,可以发现,开关管实现了软开关。ir为谐振腔电流,满载下谐振腔峰值电流为26.3 A。vCr为谐振电容两端电压。
W3——隐含层神经单元到输出层神经单元的连接权重矩阵;
f(x)——隐含层神经单元的传递函数;
g(x)——输出层神经单元的传递函数,是隐含层的线性组合。
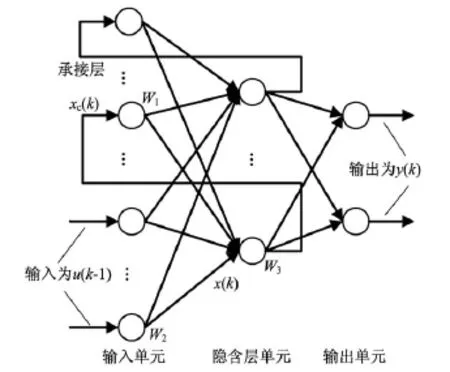
图2 Elman神经网络模型
3 客流量预测模型的设计和实现
为较好地对城市轨道交通线网客流进行分析和预测,本文以相关性理论和Elman神经网络为基础,结合轨道交通客流量预测的业务需要,提出一种客流时空相关性的客流量预测模型。(如图3所示)。可利用时间及空间相关性来分析城市轨道交通车站客流量的时间及空间相关程度,并从中寻找对预测车站的客流量量影响较大的车站历史数据及其它相关车站的时空数据。而Elman神经网络结合客流量时序变化的特点,更适用于时序变化的预测问题。
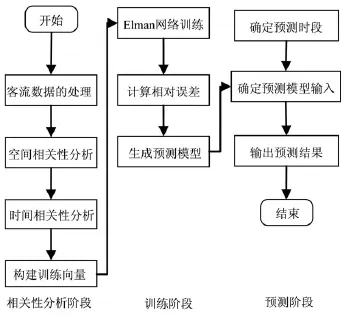
图3 客流预测模型训练及预测流程
3.1客流时空相关性分析
通过对城市轨道交通分时客流量特点进行分析,可得到城市轨道交通车站的短时出站客流量在时间上呈现一定的规律性的变化。根据广州地铁三元里站的历史客流量数据得到图4所示的相关关系。
分析广州地铁2、8号线的出站客流量数据,并构建出站客流向量。以广州地铁三元里站作为预测站点,通过Spearman相关系数计算该站周内客流量相关性及周间客流量相关性,可得到相关性系数如表1所示。
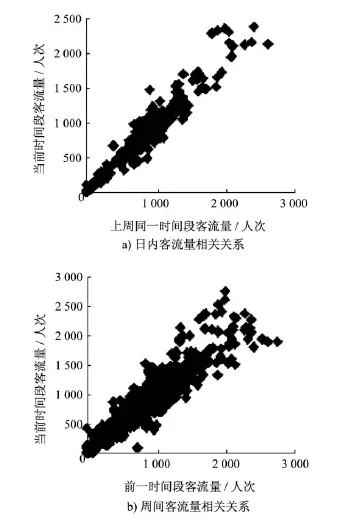
图4 客流量的时间相关关系(时间段粒度:15 min)

表1 广州地铁三元里站客流量相关性关系
同时,城市轨道交通线网由不同空间位置上的车站组成。虽然每个车站的客流规律是不同的,但由于线路存在交叉,因此车站都会受到线路或交叉线路上的车站客流的影响。根据广州地铁2、8号线的历史客流量数据,绘制三元里站的客流量与中大站的客流量的相对关系图(见图5)。从图5中可看出明显的线性关系。因此,预测目标站点的出站客流量,可将其与线网中的其它车站的进站客流进行相关性分析,从而得到客流相关度较大的车站。并对这些车站使用上述的时间相关性分析,进而得到对应车站相关度较大的客流时段。
通过获取其它车站的客流向量,分析向量之间的Spearman相关系数,得到车站相关系数结果(如图6所示)。
根据图6的站间相关系数,选择相关系数大于0.89的站点作为相关站点。故选择越秀公园站、中大站、火车站站作为相关站点进行时间相关性分析,得到相关车站客流时间相关性如表2所示。

图5 客流量的空间相关关系(时间段粒度:15 min)
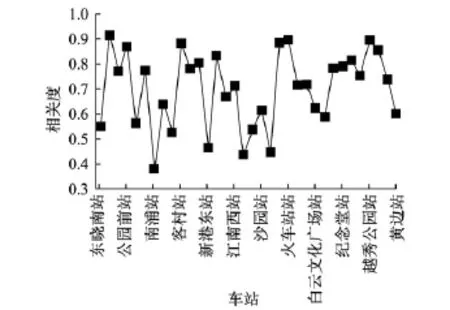
图6 站间相关系数

表2 广州地铁三元里站基于空间相关性的时间相关系数
根据表2相关度结果,取这三个车站的相关系数最大的时间段为时空相关性的输入。因此在考虑空间相关性时,选择越秀公园站前二时段、中大站前二时段及火车站站前二时段的客流量作为其它相关车站的时空数据。
3.2神经网络
对于Elman神经网络,隐藏层节点数nh=+α,0<α<10。nh、nin、nout分别表示隐层、输入层、输出层的神经单元数。隐含神经元的传递函数采用双曲正切S形函数,输出层神经元的传递函数采用线性函数。
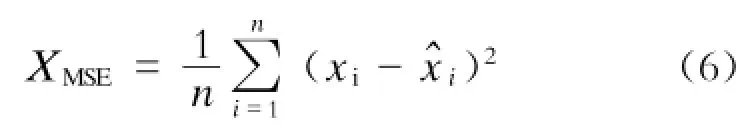
其中,x={x1,x2,…,xn}为实际客流数据,为对应的客流预测数据。
4.2三元里站分时客流预测及结果分析
通过对三元里站的出站客流进行分析,从中抽取分时客流数据样本共379组。选择299组样本作为神经网络的训练集,余下的80组样本作为测试集。测试集的时间为第10周周三的客流数据。同时,为了加快神经网络的收敛速度,在神经网络训练前将客流量归一化到[-1,1]区间内[10]。
在仅考虑时间相关性的情况下,神经网络模型的5个输入层神经元依次为上周前一时段,上周同一时段,上周后一时段、前一时段和前二时段的客流量;1个输出层神经元为目标时段预测客流量。采用自适应学习速率的动量梯度下降反向传播算法训练神经网络。经过训练之后,预测结果对测试样本的拟合程度如图7所示。
4 试验分析
4.1试验数据与评价标准
试验数据采用广州地铁交通2、8号线上的35个车站的客流量。数据的间隔为15 min。采用均方根误差(XMSE)这种公认的标准评价方法进行评价。
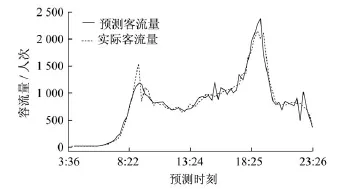
图7 考虑时间相关性的预测结果拟合曲线
在考虑时空相关性的情况下,神经网络模型的8个输入层神经元依次为上周前一时段,上周同一时段,上周后一时段、前一时段、前二时段,火车站站前一时段,中大站前一时段和越秀公园站前二时段的客流量;输出层神经元为目标时段预测客流量。采用自适应学习速率的动量梯度下降反向传播算法训练Elman神经网络。经过训练之后,预测结果对测试样本的拟合程度如图8所示。
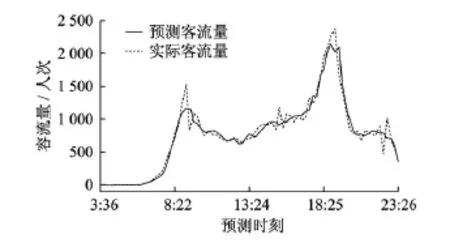
图8 考虑时空相关性的预测结果拟合曲线
由图7和图8可以看出,采用时空相关性的Elman神经网络进行车站出站短时客流量预测时的预测结果更为准确;预测客流量的均方误差相对于仅考虑时间相关性的方法降低了21%左右。神经网络性能函数比对见表3所示。

表3 神经网络性能函数比对
4.3客流多步预测
上述模型都是基于已经得到前面时刻的实际客流数据,但在实际应用时,仅预测15 min后的客流数据无法满足城市轨道交通客流疏导安排,因此提前一步(15 min)预测城市轨道交通线网的客流数据缺乏实用性。
客流量多步预测指下一步预测使用了上一步预测的结果作为输入。例如,若已知T3时刻的客流量,需要预测T时刻的客流量,则上述时空相关模型的预测输入应包含三元里站T1及T2时刻客流量及火车站站、越秀公园站、中大站T1时刻客流量。即使三元里站T2及T1客流信息是未知的,也可对T2时刻进行预测,进而根据T2的预测结果得到T1预测模型的输入,最后得到T时刻预测模型的输入。类似的,可以通过同样的方法得到火车站站、越秀公园站及中大站的T1时刻客流量。
基于上述理论,本文在单步预测的基础上,进行了提前3步的客流量预测。预测结果与实际客流量的拟合程度如图9所示。这保证了城市轨道交通运营方能有45 min安排客流疏导。
多步预测保证了客流量预测能使用当天已有客流量数据,降低了仅通过上周客流量进行客流量预测的误差。这为运营方有效组织客流疏导提供了预测数据的支持。
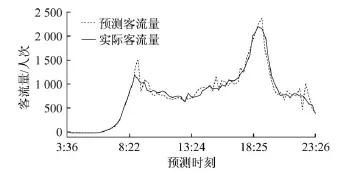
图9 提前三步客流预测结果
5 结语
本文主要针对城市轨道交通短时客流预测进行理论研究及仿真试验,其目的就在于为日渐复杂的轨道交通线网系统中时变性的客流探求适合的短时预测方法。这对于相关运营部门日常平衡运量需求和运能供给、制定合理的运营调度计划、组织日常运输生产都具有重大的意义。时空相关性预测模型的核心思想就是先用相关性分析得到神经网络的输入,再利用Elman神经网络对具有非线性特征的客流量进行预测。预测结果表明,该预测模型能够提高预测精度、减小预测误差。
[1] 袁健,范炳全.交通流短时预测研究进展[J].城市交通,2012(6):73.
[2] 张永生,姚恩建,代洪娜.成网条件下地铁换乘量预测方法研究[J].铁道学报,2013(11):1.
[3] CERVERO R.Alternative approaches to modeling the travel-demand impacts of smart growth[J].Journal of the American planning Association,2006,72(3):285.
[4] KEEMIN S,HUNJIN S.Factors generating boarding at metro station in the Seoul Metropolitan Area[J].Cities,2010,27(5):358.
[5] CHEN M C,WEI Y.Exploring time variants for short-term passenger flow[J].Journal of Transport Geograph,2011,19(4):488.
[6] 杨军,侯忠生.一种基于灰色马尔科夫的大客流实时预测模型[J].北京交通大学学报,2013(2):119.
[7] 常刚,张毅,姚丹亚.基于时空依赖性的区域路网短时交通流预测模型[J].清华大学学报(自然科学版),2013(2):215.
[8] 李晓俊,吕晓艳,刘军.基于径向基神经网络的铁路短期客流预测[J].铁道运输与经济,2011(6):85.
[9] 姜平,石琴,陈无畏,等.基于Elman型回归神经网络的公交客流预测[J].合肥工业大学学报(自然科学版),2008(3):340.
[10] 张齐,许志坚,赵坤荣.基于Elman神经网络的污染源数据预测[J].华南理工大学学报(自然科学版),2009(5):135.
[11] 刘晓华,韩梅,陈超.城市轨道交通车站联合客流控制研究[J].城市轨道交通研究,2014(5):106.
Spatial-temporal Correlation Prediction for Passenger Flow in Urban Rail Transit Network
Zou Dong,Liu Qiong,Huang Zirong
passenger flow prediction is a complex spatialtemporal correlation problem.At present,it is difficult to obtain valuable prodiction only from the historical data of target stations.In this paper,a spatial-temporal correlation prediction model based on neural network is proposed,in which the model input is composed by two parts:the current station historical data and the spatial-temporal data from other relevant stations.The former is extracted from the data of current station in past three weeks which have strong longitudinal time correlation,while the later is extracted from the 3-week data of other relevant station which have strong horizontal time correlation,both are using the Spearman algorithm.Elman natural network algorithm is adopted to compare the performance of spatialtemporal correlation prediction and time correlation prediction.The experimental results show that the proposed spatial-temporal prediction model is more accuracy than the time prediction model.Finally,multi-step passenger flow prodiction is realized on the basis of spatial-temporal prediction to supportr urban rail transit with data and ample time.
urban rail transit network;correlation analysis;passenger flow predication;neural network
U 293.13∶U 231
10.16037/j.1007-869x.2016.03.007
*广东省公益研究与能力建设项目(2014A010101016);广州地铁集团有限公司与华南理工大学合作项目(J11KFA6D004)
(2014-11-05)

