一种基于解析积分的TDPO算法及其在散射问题中的应用

覃璐瑶 魏兵 边成 王婷

(西安电子科技大学物理与光电工程学院电波研究所,西安 710071)



一种基于解析积分的TDPO算法及其在散射问题中的应用

覃璐瑶 魏兵 边成 王婷

(西安电子科技大学物理与光电工程学院电波研究所,西安 710071)

基于时域物理光学(Time-domain Physical Optics,TDPO)方法,给出了三角面元剖分下散射场解析计算的求解思路.对三角面元进行二重积分求得散射场计算的最终表达式.与传统的TDPO方法相比,在同等计算模型下,解析方法具有更高的计算精度.在处理高频复杂问题时,解析方法可以用更少的面元数量参与计算,从而节省大量的计算时间与计算机内存.

解析;时域物理光学算法(TDPO);散射;频率无关

DOI 10.13443/j.cjors.2015071003

引 言

实际的飞行目标在常见的雷达波段常常是电大尺寸目标,其散射特性的求解采用数值方法存在计算量大的困难,目标特性仿真需要耗费大量的计算资源和计算时间.当目标为电大尺寸且外形相对简单时采用高频计算方法(例如物理光学法)是良好的选择方案之一.若需要获得目标的时域回波,则仿真时采用时域方法将更有效.时域物理光学(Time-Domain Physical Optics,TDPO)方法是物理光学(Physical Optics,PO)方法的时域版本,便于获得目标的时域回波和宽带信息.传统的TDPO算法在求解时将目标划分成许多个小的三角面元,为了计算简便,三角面元中每一点的入射场大小看作是一致的(即用某一点场值代替整个面元的场),或者采用高斯积分的办法,用三角面元上多个特征点的场来拟合整个三角面元的远场散射.为保证计算精度,需要将面元的特征尺寸取十分之一波长以下.显然,经典的PO算法在计算超电大目标的散射特性时同样存在计算量大的瓶颈问题.拟合目标的三角面片之所以不能取的比较大是由于上述的场累加方式,当采用解析方式进行面片内场值累加时就可以采用大面片计算,从根本上降低内存需求.在PO方法解析积分计算方面,Gordon、Ludwig等给出了振幅相位都是线性变化的PO解析方法[1-2].吴语茂、Felipe等给出了与频率无关的PO方法并应用于电大尺寸目标电磁特性的计算[3-5].本文在吴语茂等人[3-4]工作的基础上实现了基于解析积分的TDPO计算,极大地提高了TDPO算法的计算效率.

解析TDPO算法的主要思路是:首先,将计算目标剖分成三角面元并将面元在特定坐标面上投影;其次,将与积分无关的常向量提取出来,并将算式中的时间延迟用三维空间坐标替代;最后,在入射源为平面高斯脉冲的情形下对三角面元进行空间二重积分.

1 解析TDPO算法的基本理论

TDPO方法观察点的场是目标上亮区三角形面片积分的累加结果,计算时的坐标、目标上的特征面元、入射波和观察方向等如图1所示,远区散射场可以由式(1)计算[6]：

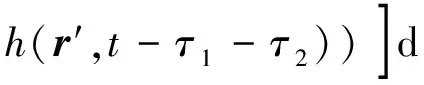
(1)

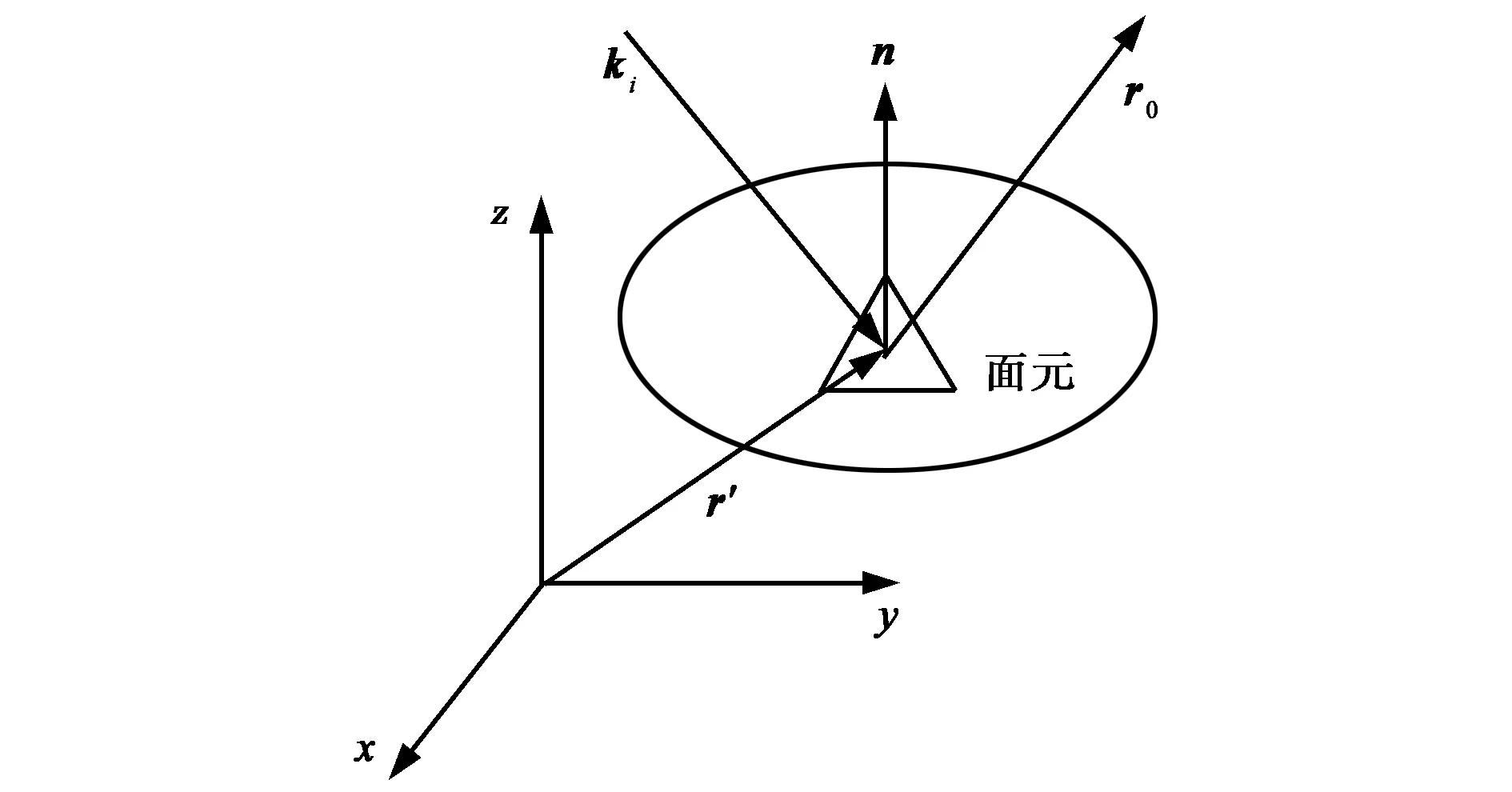
图1 TDPO计算各参量示意图

式中: r0为散射方向; h(r′,t)为入射脉冲; n(r′)为散射体上某一点的单位法向量; Z0为自由空间波阻抗; C0为真空波速; τ1、τ2分别是积分点到观察点的时域与源点到积分点的时间延迟[7],算式如下:

(2)

对于给定面元,入射磁场方向、面元法向、散射方向都是已知的,即散射场公式可以写成

(3)

h0为入射磁场的方向.

三角面元所在的平面方程可以表示为

Ax+By+Cz+D=0.

(4)

将三维空间中的三角形投影到xoy平面(也可投影到其他平面)进行积分,式(1)可以改写为

τ1-τ2)dxdy.

(5)

对于特定面元,式(5)中右端积分号外面的部分实际上是一个常矢量,此时式(5)可以简写为

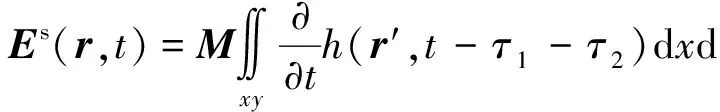
(6)

式中,

(7)

而由式(2)可知,τ1、τ2都是与面元上点坐标位置相关的标量,那么式(6)中的时间延迟可以用位置坐标来表示,即

t-τ1-τ2=t+ax+by+c.

(8)

此时,式(6)改写为

by+c)dxdy.

(9)

至此,远区散射场的计算转化成了与空间位置和入射波时间导数相关的积分问题.投影到坐标面上后,一个典型的三角形的位置如图2所示.此时积分函数在x方向的上下限由三角形顶点坐标决定,而y方向的积分限则由相关的直线方程决定.面元积分可以写为

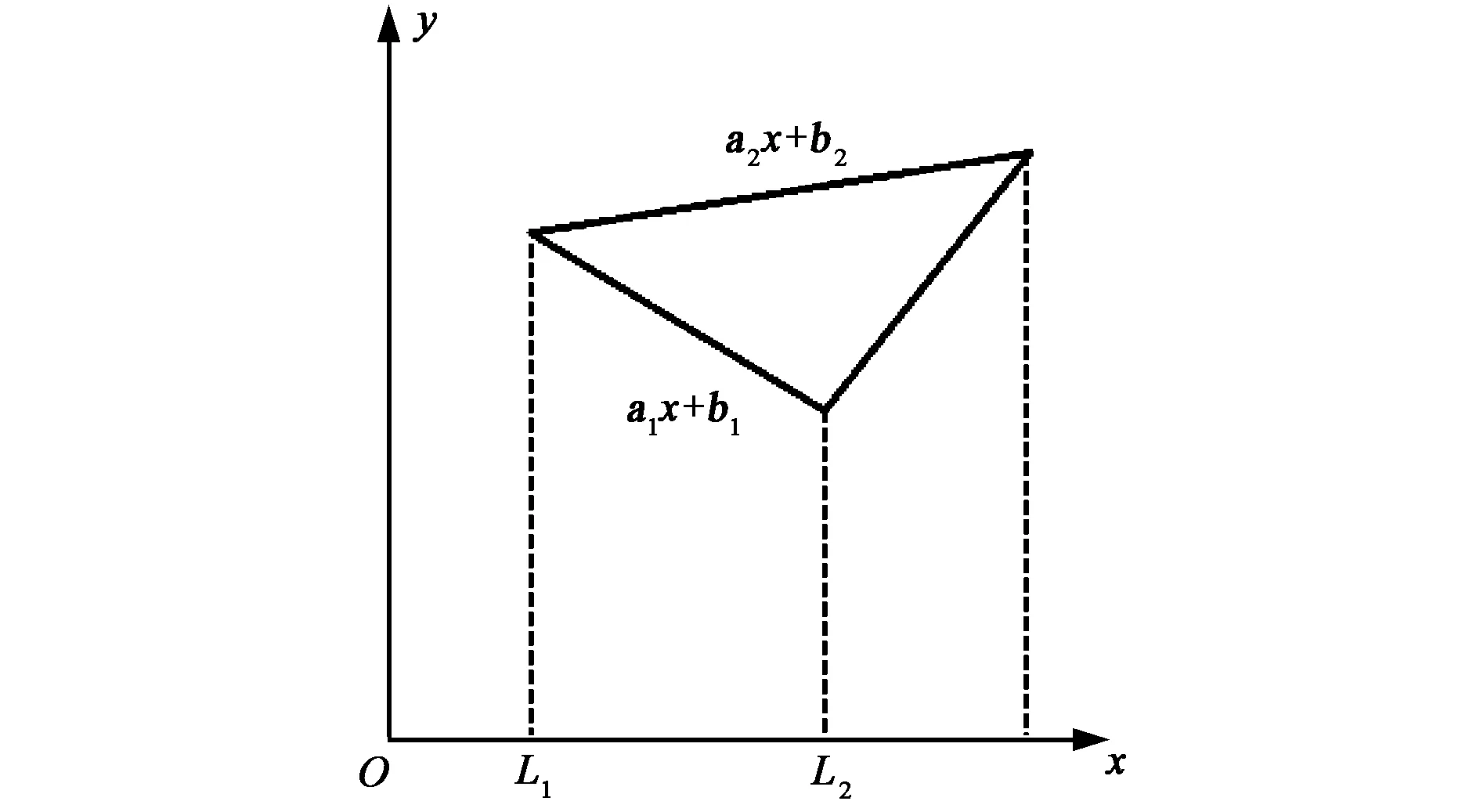
图2 投影后三角形的坐标关系

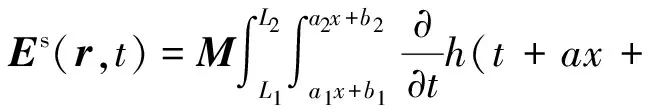
by+c)dydx.

(10)

为便于解析地完成式(10)中的积分项,假定入射波为微分高斯脉冲,即

(11)

式中,τ为脉冲宽度.

对于上述形式的入射波,有

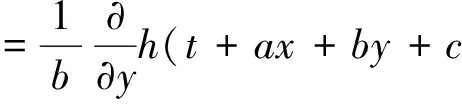
(12)

式(10)中入射波对时间偏导用空间偏导代替后有

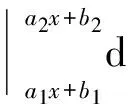
(13)

积分可得

(14)

式中,

(15)

式(14)即TDPO的散射场计算式.显然,每个三角面元的散射场都是通过解析得到,因而,本文方法是与频率无关的.

2 算例检验

算例1 金属板的后向散射

金属板大小为5 m×5 m,电磁波垂直于板面入射,电场沿平行于板棱边的方向极化.计算频率上限为400 MHz.传统TDPO计算时将板划分为20 000个三角面元,解析TDPO计算时将金属板仅划分为2个三角面元.图3是金属平板的后向散射场时域波形,图4是后向雷达散射截面积(Radar Cross-Section,RCS).图中三角形和圆点分别表示解析TDPO和传统TDPO的计算结果,作为比较图中还给出了FDTD的结果(实线).

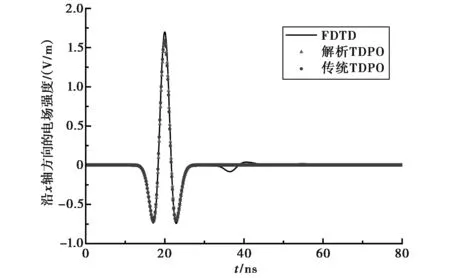
图3 金属平板的后向散射场

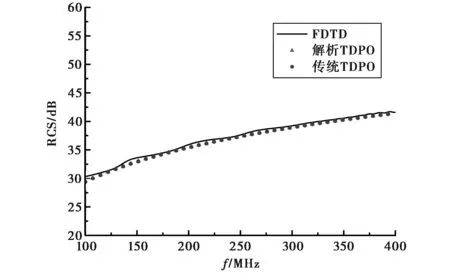
图4 金属平板的后向RCS

由图3、4可见,三者的计算符合得很好.值得注意的是,解析TDPO与传统TDPO计算的面元数目相差万倍.本算例说明了解析TDPO算法的高效性.

算例2 金属球的后向散射

金属球半径为1 m,解析TDPO计算时球剖分尺度为0.02 m(约4万个面元),传统TDPO计算时剖分尺度为0.01 m(约17万面元).图5为解析TDPO和传统TDPO计算结果的比较,作为参考图中还给出了几何光学法(Geometrical Optics, GO)的结果.

从上述算例可知,尽管解析TDPO能准确求解出单一面片的直接散射场,但考虑到实际目标多为曲面目标,计算时仍需将目标表面剖分的足够精细以得到较好的计算结果.

算例3 B2轰炸机的后向RCS

B2飞机的模型如图6所示.平面波垂直于飞机所在平面入射,电场沿飞机轴向极化.图7是该飞机的后向RCS.作为比较,图8给出了低频端矩量法(Method of Moments, MoM)方法的计算结果.

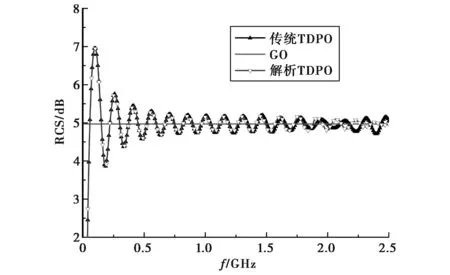
图5 金属球的后向RCS

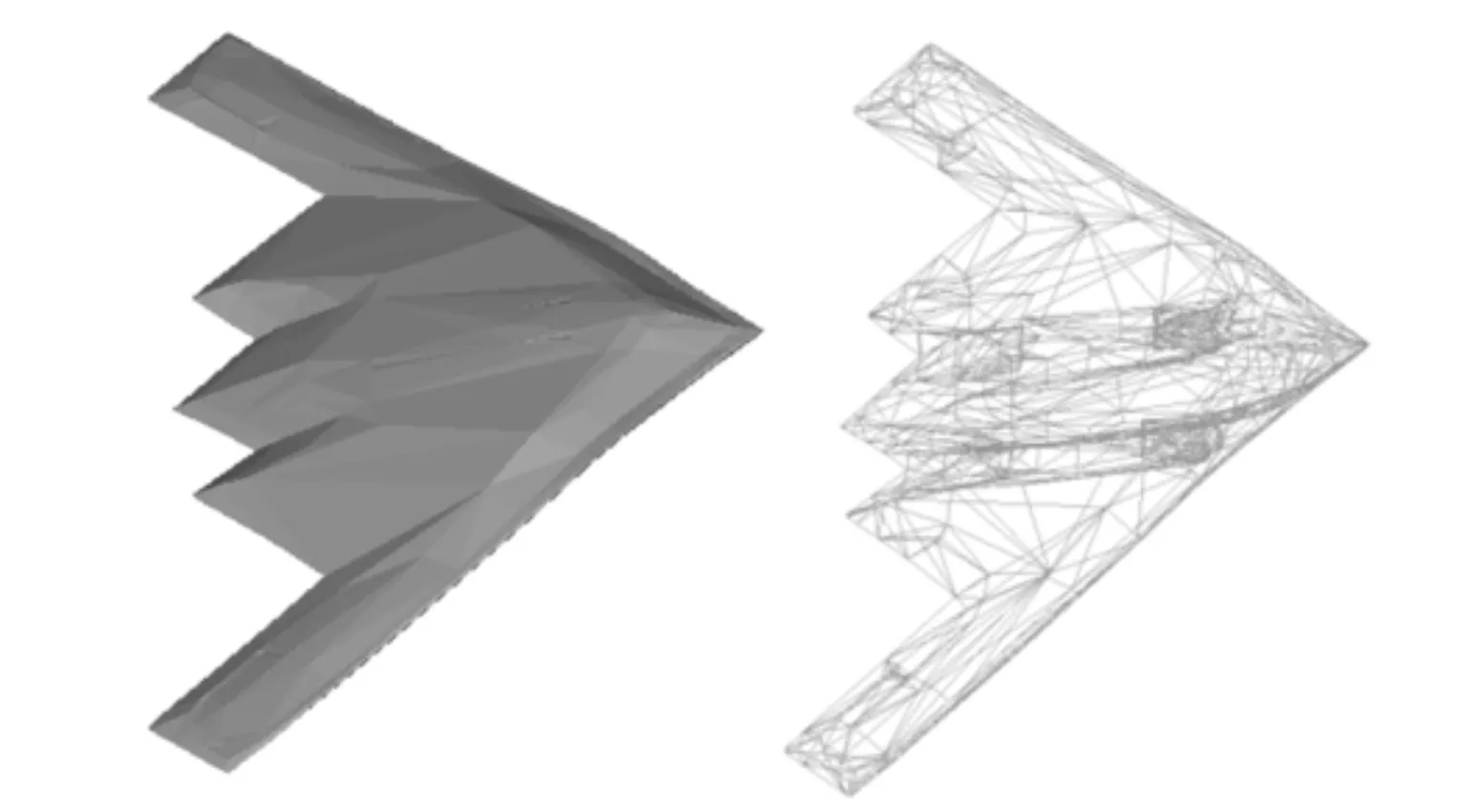
图6 B2轰炸机面元模型

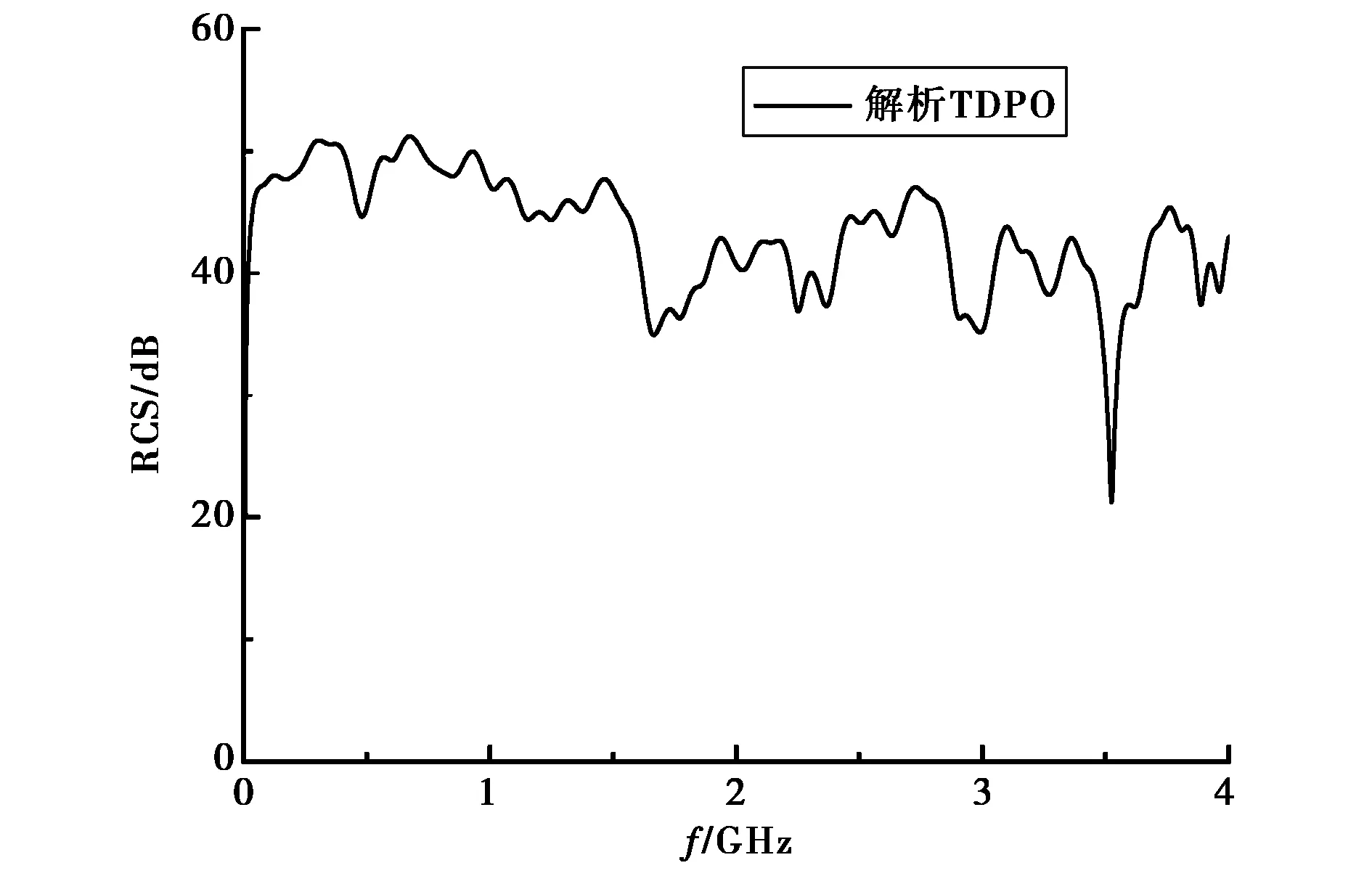
图7 B2的后向RCS

图8 低频范围后向RCS与MoM的比较

改变平面波的入射方向,分别计算迎着轰炸机机头水平入射以及斜向上15°入射时的后向RCS,其中电场方向均垂直入射方向向下.图9即是两种情形下的后向RCS.

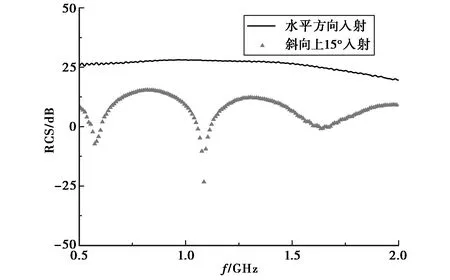
图9 改变入射方向得到的后向RCS

3 结 论

本文实现了基于解析积分的时域物理光学计算.金属板、金属球和复杂目标后向宽带散射的算例表明，本文方法在保守PO方法计算精度的同时极大地提高了TDPO算法的计算效率.

[1]GORDON W B. Far-field approximations to the Kirchhoff-Helmholtz representation of scattered fields [J]. IEEE transactions on antennas and propagation, 1975, 23(4): 590-592.

[2]LUDWIG A C. Computation of radiation patterns involving numerical double integration[J]. IEEE transactions on antennas and propagation, 1968, 16(6): 766-769.

[3]VICO F, FERRANDO M, VALERO A. A new fast physical optics for smooth surfaces by means of a numerical theory of diffraction[J]. IEEE transactions on antennas and propagation, 2010, 58(3):773-789.

[4]WU Y M, JIANG L J, CHEW W C. An efficient method for computing highly oscillatory physical optics integral[J]. Progress in electromagnetics research, 2012, 127(2): 211-257.

[5]WU Y M, JIANG L J. The numerical steepest descent path method for calculating physical optics integrals on smooth conducting quadratic surfaces[J]. IEEE transactions on antennas and propagation, 2013, 61(8): 4183-4193.[6]SUNEY,RUSCHWVT.Time-domainphysical-optics[J].IEEEtransactionsonantennasandpropagation, 1994, 42(1): 9-15.

[7] 杨凌霞.TDPO关键技术及TDPO/FDTD混合算法研究[D]. 西安: 西安电子科技大学,2007.

YANGLX.StudyofkeytechniquesofTDPOandahybridTDPO/FDTDapproach[D].Xi’an:XidianUniversity, 2007. (inChinese)

[8]连科峰, 张红霞, 陈益邻.NURBS曲面RCS的物理光学法混合计算[J]. 电波科学学报, 2006, 21(1): 135-139.

LIANKF,ZHANGHX,CHENYL.HybridPOsolutionforRCSofNURBSsurfaces[J].Chinesejournalofradioscience, 2006, 21(1): 135-139.(inChinese)

[9]刘春阳, 焦永昌, 张朋, 等. 一种飞翼布局无人机的RCS研究[J]. 电波科学学报, 2009, 24(1): 95-98.

LIUCY,JIAOYC,ZHANGP,etal.ResearchonRCSofaUAVformedinflyingwingconfiguration[J].Chinesejournalofradioscience, 2009, 24(1): 95-98.(inChinese)

覃璐瑶 (1992-),男,湖南人,西安电子科技大学物理与光电工程学院硕士研究生,研究方向为PO、TDPO.

A TDPO algorithm based on analytic integral and its application in scattering problems

QIN Luyao WEI Bing BIAN Cheng WANG Ting

(School of Physics and Optoelectronic Engineering, Xidian University, Xi’an 710071, China)

Based on the time-domain physical optics (TDPO) algorithm, the method for the analytic scattering field of the triangular surface element is given in this paper. The expression for the calculation of the scattering field is obtained by the double integral of the triangular surface element. Compared with the traditional TDPO method, this method has a higher accuracy. In dealing with the problem of high frequency and complex target, this method requires less triangle surface elements, and can save computation time and computer memory.

analytical; TDPO; scattered field; frequency independent

10.13443/j.cjors.2015071003

2015-07-10

国家自然科学基金(61231003，61401344)

O451

A

1005-0388(2016)03-0508-05

覃璐瑶, 魏兵, 边成, 等. 一种基于解析积分的TDPO算法及其在散射问题中的应用[J]. 电波科学学报,2016,31(3):508-511+561.

QIN L Y, WEI B, BIAN C, et al. A TDPO algorithm based on analytic integral and its application in scattering problems[J]. Chinese journal of radio science,2016,31(3):508-511+561.(in Chinese). DOI: 10.13443/j.cjors.2015071003

联系人： 覃璐瑶 E-mail: qinluyao123456@163.com