机载正下视SAR探测极地冰川的回波数值模拟

吴超 张晓娟 方广有

(1.中国科学院大学,北京 100039;2.中国科学院电子学研究所,北京 100190)



机载正下视SAR探测极地冰川的回波数值模拟

吴超1,2张晓娟2方广有2

(1.中国科学院大学,北京 100039;2.中国科学院电子学研究所,北京 100190)

建立了大尺度分层粗糙面散射物理模型,基于Kirchhoff近似、几何光学和射线追踪方法,推导给出粗糙面散射场的计算公式,提出了一种快速模拟机载正下视合成孔径雷达(Synthetic Aperture Radar, SAR)探测冰川回波的数值仿真方法,以帮助分析实测数据. 对SAR系统设计、雷达回波信号处理算法研究都有很大帮助,可以应用到星体地下结构探测回波的模拟. 理论公式及数值仿真结果验证了此数值仿真方法的正确性. 在不同的仿真场景和雷达系统参数下,数值仿真模拟了冰川散射回波,定量分析了冰层表面粗糙度、次表面粗糙度、山体倾斜度、雷达系统参数等对天底区域和非天底区域散射回波的影响. 本文的仿真方法可以快速计算任意大尺度特定地形所对应的雷达探测仪回波数据.

合成孔径雷达;SAR回波模拟;非均匀分层介质;随机粗糙面散射;Kirchhoff理论

DOI 10.13443/j.cjors.2015072202

引 言

粗糙面电磁散射是电磁学领域的一个热门研究课题,其在微波遥感、目标识别分类、生物医学、环境军事、医学和航天领域都有广泛的应用.分层介质粗糙面的散射是该领域的研究重点之一,在医学成像、无损探伤、探地雷达、地球物理与遥感科学、宇宙空间科学探测等方面有重要的应用价值[1-10]. 粗糙面电磁散射的计算方法主要分为两大类：近似解析方法和数值方法. 近似解析方法是根据粗糙面的粗糙程度,采用不同的物理近似来得到散射场的近似解. 常用的近似解析解方法有基尔Kirchhoff近似[1],微扰法[2],双尺度方法[3]. 数值方法主要分为两大类:微分方程法,积分方程法[4]. 常用的数值方法有有限元法、时域有限差分法、矩量法. Nouvel等[5-6]用小面元(Facet method)模型,给出了火星表面雷达探测仪回波的数值模拟,但只适用于高度起伏不大的相对平缓的表面,并且没有给出次表面回波的计算. Picardi等[3]的方法只能定性分析表面和次表面回波的统计特征,而无法计算一个特定地形所对应的雷达探测仪回波. 目前国内外很少有文献关于数值模拟机载合成孔径雷达(Synthetic Aperture Radar, SAR)[7]探测冰川覆盖冰层厚度雷达[8]回波的研究,本文基于Kirchhoff近似、几何光学和射线追踪方法[2],提出一种快速模拟机载SAR探测冰川回波的方法,以帮助分析实测数据,对于SAR系统设计、雷达回波信号处理算法研究都有很大帮助,可以应用到行星地下结构探测回波模拟.

1 物理模型与计算方法

1.1 物理模型

图1给出了机载SAR探测冰川冰层厚度的物理模型示意图,山体具有一定的倾斜度,冰层的复介电常数为ε1,冰层覆盖下的次表层的复介电常数为ε2,山体的复介电常数为ε3,飞机飞行的高度为H,飞行速度为v,雷达天线发射电磁波照射冰川,接收天线系统接收来自冰川表面和次表面的散射回波信号.

图1 机载正下视雷达探测分层粗糙面电磁散射物理模型

由于实际的冰川表面和次表面粗糙度满足大尺度特性,因此本文中建立大尺度分层媒质粗糙面散射回波数值仿真计算模型. Kirchhoff近似是指粗糙面上任意一点处的表面场可以用该点的切面场表示,适用的条件是kl>6.28,l2>2.76σλ,即粗糙面上每一点的曲率半径大于入射波长,k和λ分别为电磁波的波数和波长,σ和l分别为随机粗糙面的均方根高度和相关长度. 本文的仿真方法是将三维(3D)粗糙面剖分成任意多个小的三角面元,三角面元的尺度要远小于入射波的波长.

1.2 冰川表层散射回波计算

长度为L,加载电流为I的偶极子天线所在极坐标系(r,θ,φ)中,偶极子的辐射场可以表示为

(1)

式中: k为空气中的波数; μ0和ε0分别为空气中的磁导率和介电常数.

由Kirchhoff近似,入射到三角面元i的电场经过面元反射得到反射场为

(2)

依据Stratton-Chu积分公式[9],三角面元i在接收天线处的辐射场为

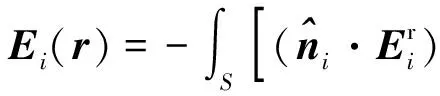
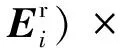
(3)

(4)

通过式(4)可以看出,只要计算出粗糙面的反射场或者经次表面反射的透射场,就可以计算出空间中任意位置的场分布. 具体做法是:粗糙面剖分成三角面元,如图2所示,在面OAB上,与雷达距离相同的面元的散射回波到达天线的时间延迟也是相同的,回波经相干叠加后得到该距离下天线接收到的回波的强度,采取相同的步骤依次计算出雷达距离面元的最小距离rmin和最大距离rmax,将距离雷达在rn～rn+Δr(Δr足够小,例如Δr=1 m)之间的面元对散射场的贡献矢量叠加在一起,就可以计算得到分布在rmin～rmax之间的散射场E(rn).

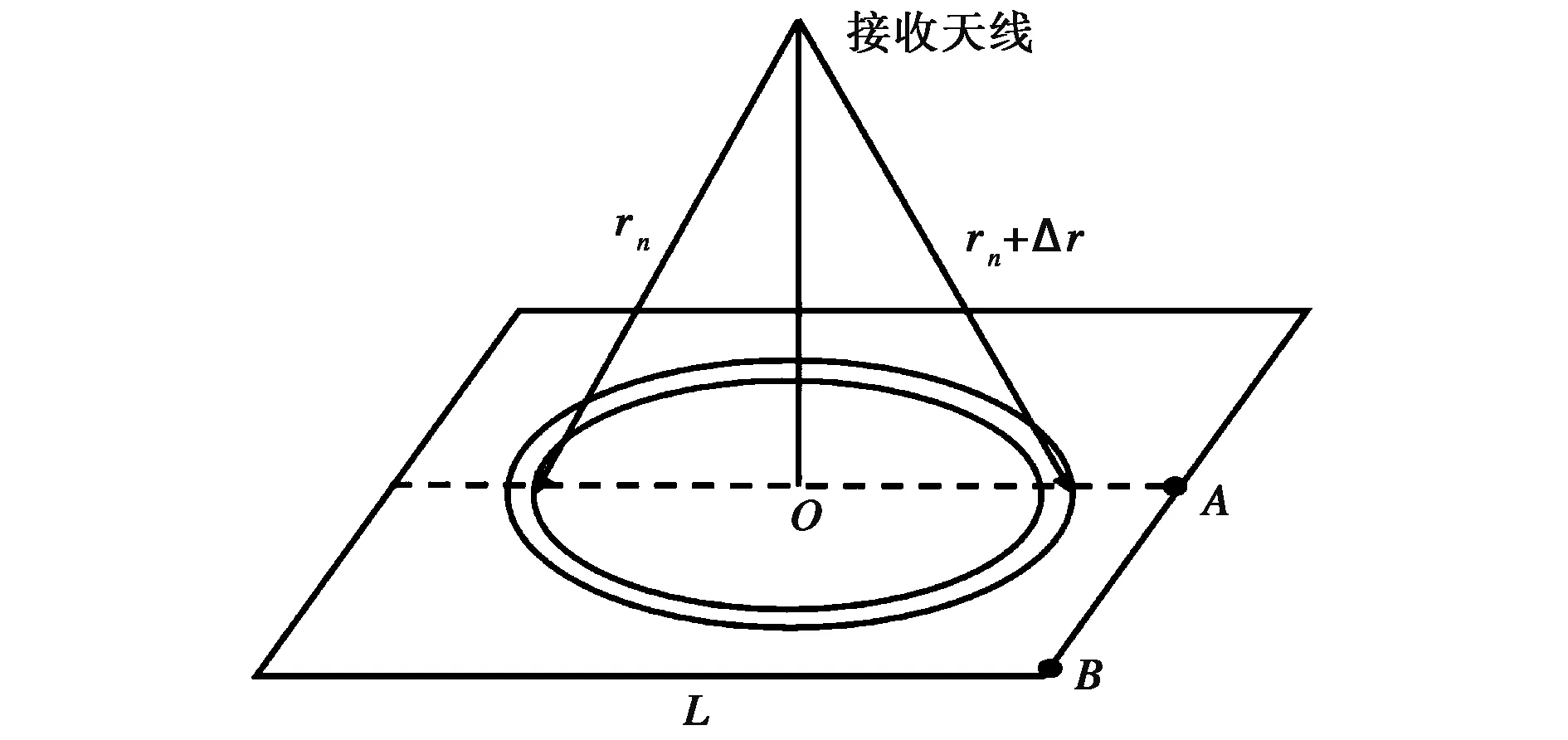
图2 雷达散射场计算几何关系示意图

1.3 次表层散射回波计算

在Kirchhoff近似下,对于粗糙面上每一个面元,可以通过Fresnel反射模型计算局部切平面的反射场和透射场. 为了提高计算速度和减少计算量,考虑次表面每个面元的散射只有在镜向方向是最强的,其他方向的散射波都很小,因此计算次表面回波时只考虑次表面镜像反射的回波透过表层的散射传输回波.

计算得到次表面反射场在表层的透射场,依据Stratton-Chu积分公式可以求出次表面在空间任一点的散射场分布.

1.4 回波信号的合成

采用线性调频信号可以使雷达冰川探测仪有足够的距离分辨率和发射能量,雷达探测仪采用的线性调频脉冲信号为

Tr(t)=

(5)

式中: W(t)为发射脉冲包络,包络形式为升降余弦调制; f0为起始频率; K为调频率; T为脉冲宽度.

探测仪最终接收到的时域电场强度可以表示为冲击响应和线性调频信号的卷积,有

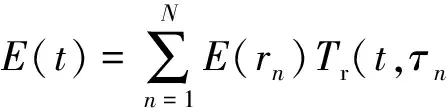
(6)

式中: τn=2rn/c为时延; rn为雷达探测仪到仿真区域各三角面元的距离.

选择参考信号为

(7)

对E(t)进行脉冲压缩,可以得到雷达探测仪的回波强度随射程(时延)的变化关系. 其中τref为参考信号的起始时间,S0为参考信号的幅度.

1.5 仿真方法的数值验证

选取天线发射的电磁波中心频率f0=30 MHz,带宽B=10 MHz,持续时间为T=2.5×10-5s,偶极子天线长度为L=5 m,天线发射功率P=500 W,选取雷达高度H=12 km,表面仿真区域大小为L=10 km的方形平面区域,表层介质复介电常数ε1=3.17+0.003i,次表层介质复介电常数ε2=8.0+0.5i,冰层厚度为D=800 m,粗糙冰表面相关长度为60 m,表面均方根高度σ=0.2 m,次表面为平面.

偶极子天线入射到该仿真区域时,雷达探测仪接收到的电场强度随距离的变化关系为[10]

(8)

式中: Δr为距离间隔; θin为入射角度且cos θin=H/r; Rv(θin)和Rh(θin)分别是垂直和水平极化反射系数.

图3给出了本文的仿真结果(图中红色虚线)和通过式(8)计算得到的理论值(图中黑粗实线)的比较．以下是对该比较图的分析:

1) 图中的横坐标表示雷达距离表面各面元的距离分布,因为雷达高度H=12 km是固定的,所以画图时减去了这个高度,图中横坐标的零点对应于天底点回波,因此横标对应的是雷达回波相对于天底点回波的时间延迟(单程). 图中纵坐标是天线接收到的回波电场值,单位是V/m.

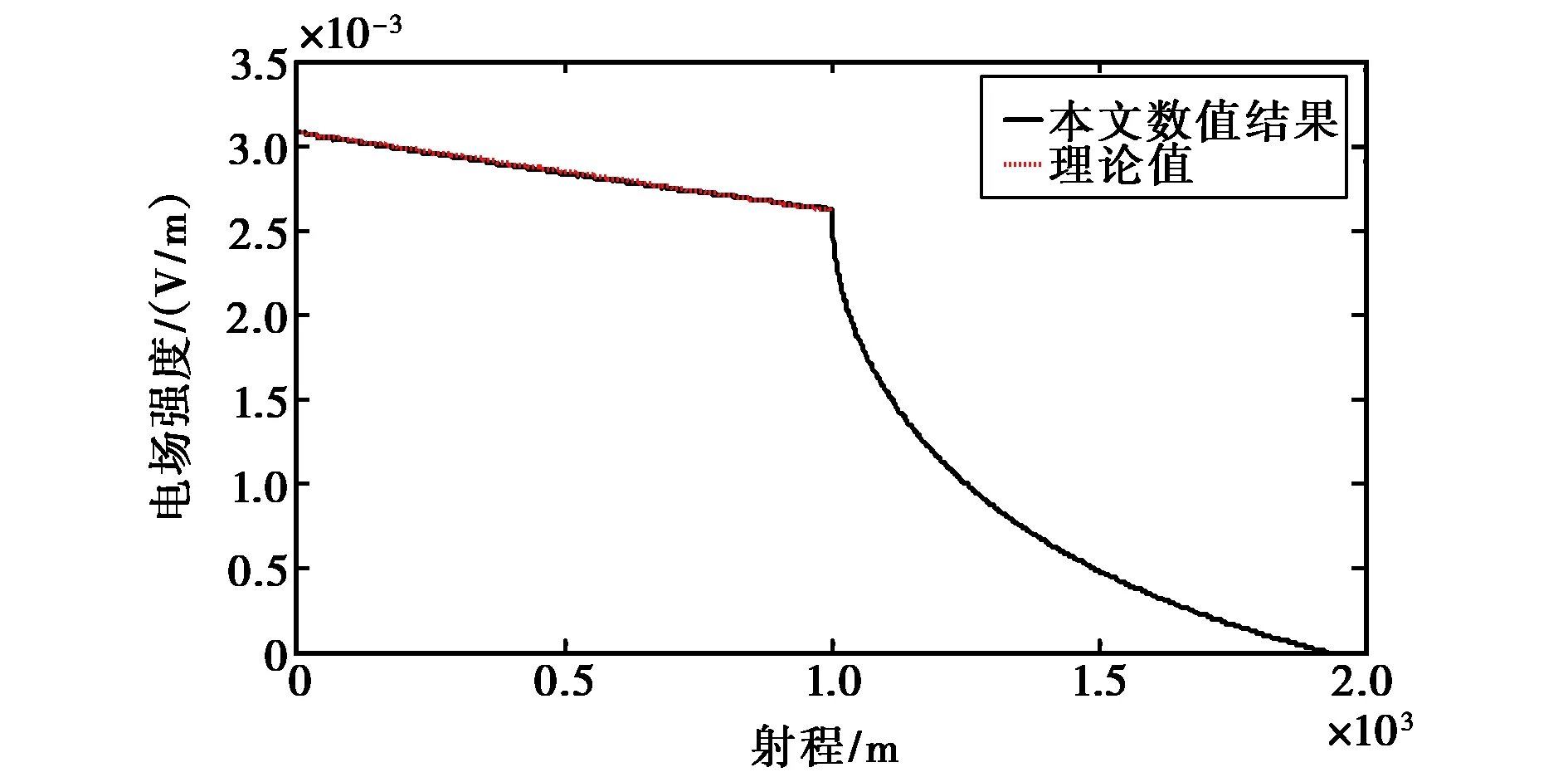
图3 表面回波仿真方法的验证

2) 图中虚线表示本文的仿真结果,粗实线表示通过式(8)计算得到的结果,从图中可以看出,这两个结果在0～1 000 m的范围间是完全吻合的.

3) 理论上来说,雷达照射的区域应该是圆形区域,但从图2雷达散射场计算几何关系示意图可以看到,由于仿真区域设置的是方形,图中OA段(对应于本仿真算例是0～1 000 m)是完整的仿真区域,而A-B段(对应距离是1 000～1 928 m)由于数值仿真区域的有限出现了仿真截断,导致数值计算结果出现突然下降的现象.

综合以上分析可以看出,采用本文仿真方法计算的表面回波与理论计算结果是完全吻合的.

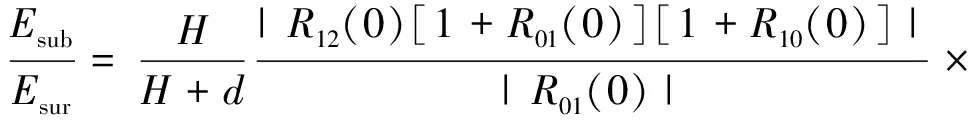
(9)

式中: H是雷达高度; d是表层的厚度(即次表面的深度); τD是次表面天底点回波较表面天底点回波的时延; ω是电磁波的角频率; tan δ是表层介质的损耗正切值; Rij(0)是电磁波从i介质垂直入射到j介质时的反射系数．将表层介质复介电常数3.17+0.003i和次表层复介电常数8+0.5i带入式(9)可以得到Esub/Esur=0.191 1. 图4给出了本文方法得到的表面回波和次表面回波的计算结果.

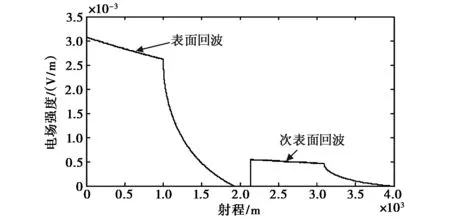
图4 表面回波和次表面回波仿真方法的验证

以下是对图4结果的分析:

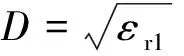
2) 次表面回波在射程距离为3 089 m处出现了骤降现象,原因也是数值仿真的截断造成的;

3) 通过计算结果得到表面天底点回波值Esur=3.056×10-3V/m,次表面天底点回波值Esub=5.858 4×10-4V/m,这样Esub/Esur=0.191 7,可以看出无论是次表面回波时延数据还是次表面回波的大小,都与理论值吻合.

2 数值计算与对比分析

2.1 次表面的粗糙度对冰川次表层回波探测影响

在仿真过程中,天线发射的电磁波中心频率f0=150 MHz,带宽B=30 MHz,持续时间为T=2.0×10-5s,偶极子天线长度为L=1 m，天线发射功率P=400 W,表面数值仿真区域大小为L=3 km的方形区域,山体的倾斜度为tanθ=2.0,粗糙表面相关长度为60 m,表面均方根高度σ=0.2 m,次表面为平面,冰层深度为100 m(下文无特别说明,仿真场景不变). 冰层复介电常数ε1=3.17+0.003i,次表层复介电常数ε2=8.0+0.5i,山体复介电常数ε3=9.0+0.5i.

如图5所示,峰值1为冰表面天底点回波峰值,峰值2为冰底层天底点回波峰值,峰值3为山体回波峰值,峰值4为山体与冰面交界处的的跳变经脉冲压缩出现的虚假峰值,峰值5为数值仿真区域有限而出现的仿真截断,实际的雷达回波中不会出现这种虚假的峰值. 从图中可以看出：粗糙的次表面使得次表面的非天底点散射也出现了一些峰值;随着次表面粗糙度的增加,角度性的漫散射使次表面的天底点回波强度减小. 随着次表面粗糙度的增加,次表面粗糙度对回波的影响变得不明显. 次表面散射场强度随着其粗糙度的增加而减小,粗糙度越大,减小的幅度也越大.

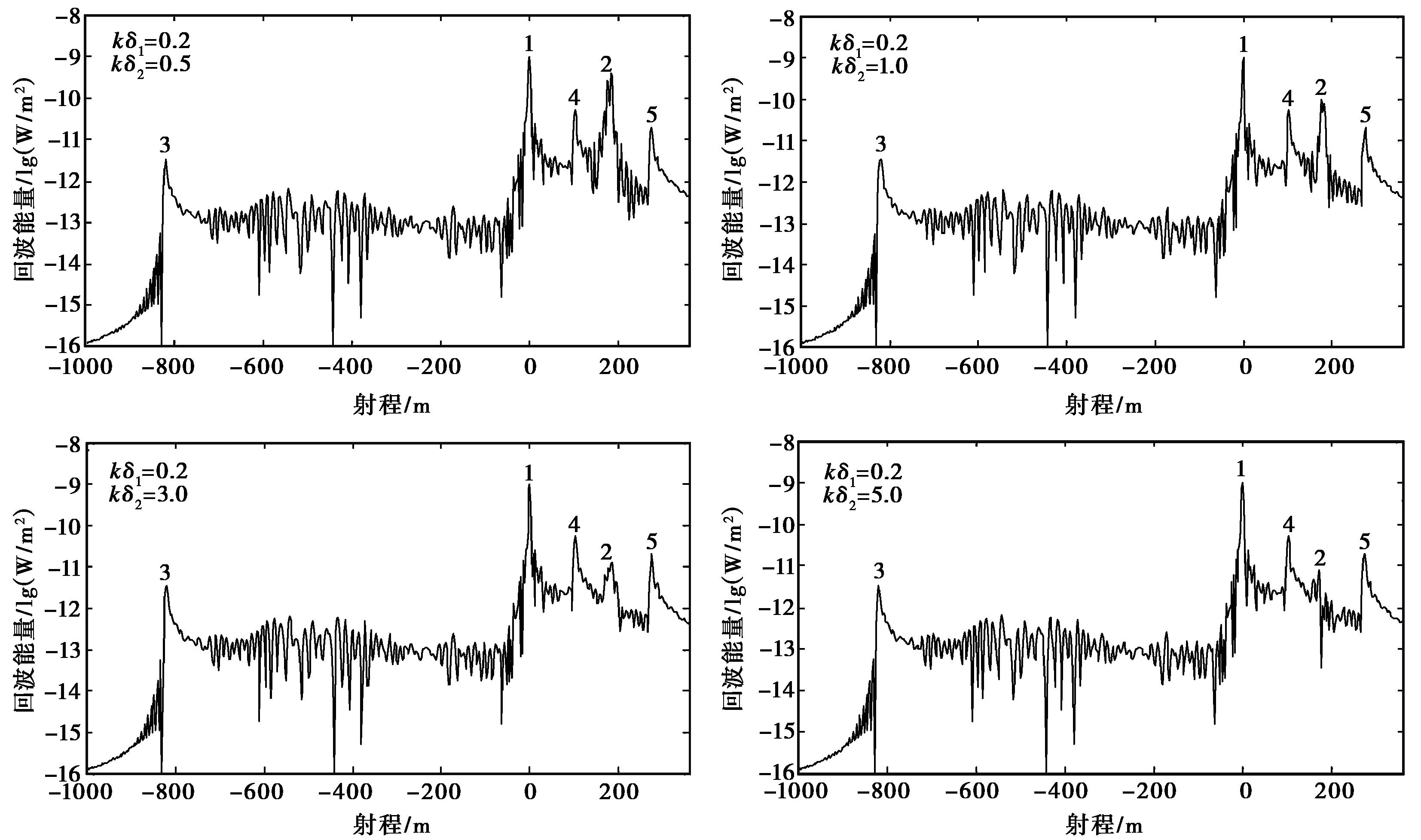
图5 冰川次表面粗糙度对回波的影响

2.2 表面的粗糙度对探测冰川次表层回波的影响

如图6所示,可以看出表层粗糙度很小时,次表层更能分辨出来,但是随着表层粗糙度增加,表面非天底点回波能量增加,淹没次表层的回波,无法分辨次表层回波. 可以尝试根据冰川表面杂波和次表面天底点回波的特性(如冰川表面杂波为非相干波,而次表面天底点回波为相干回波),通过多次观测取平均值来消除表面杂波的影响,也可以沿雷达探测仪飞行的方向采用多普勒信号处理技术,来锐化波束以消除非天底点杂波的影响.

图6 冰川表面粗糙度对回波的影响

2.3 雷达探测仪发射脉冲的带宽对回波的影响

从图7和8可以看出,随着带宽增加,雷达探测仪距离分辨率变大,冰层表面的一些细节特征也凸现出来.因此,为了探测冰层表面的细节特征,应该使雷达探测仪的带宽尽可能大,但是,带宽的增加,必然会要求中心频率的提高,而中心频率提高,会使得电磁波的穿透深度减小.因此,带宽的选择应该综合考虑距离分辨率与探测深度的要求.

图7 带宽B=20 MHz时不同表面粗糙度下冰川回波

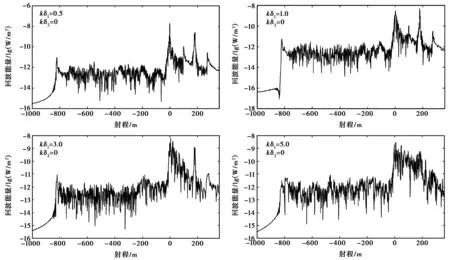
图8 带宽B=60 MHz时不同表面粗糙度下冰川回波

2.4 山体倾斜度对雷达探测回波的影响

图9中峰值1为冰层表面天底点回波,峰值2为次表层的天底点回波,峰值3为坡度为30°的山体回波,峰值4为坡度为10°的山体回波,峰值5为冰层与山体连接处的跳变产生,峰值6为仿真区域有限产生的截断效应.不同倾斜度山体产生的强散射杂波光程时延不同,对次表层探测产生干扰.

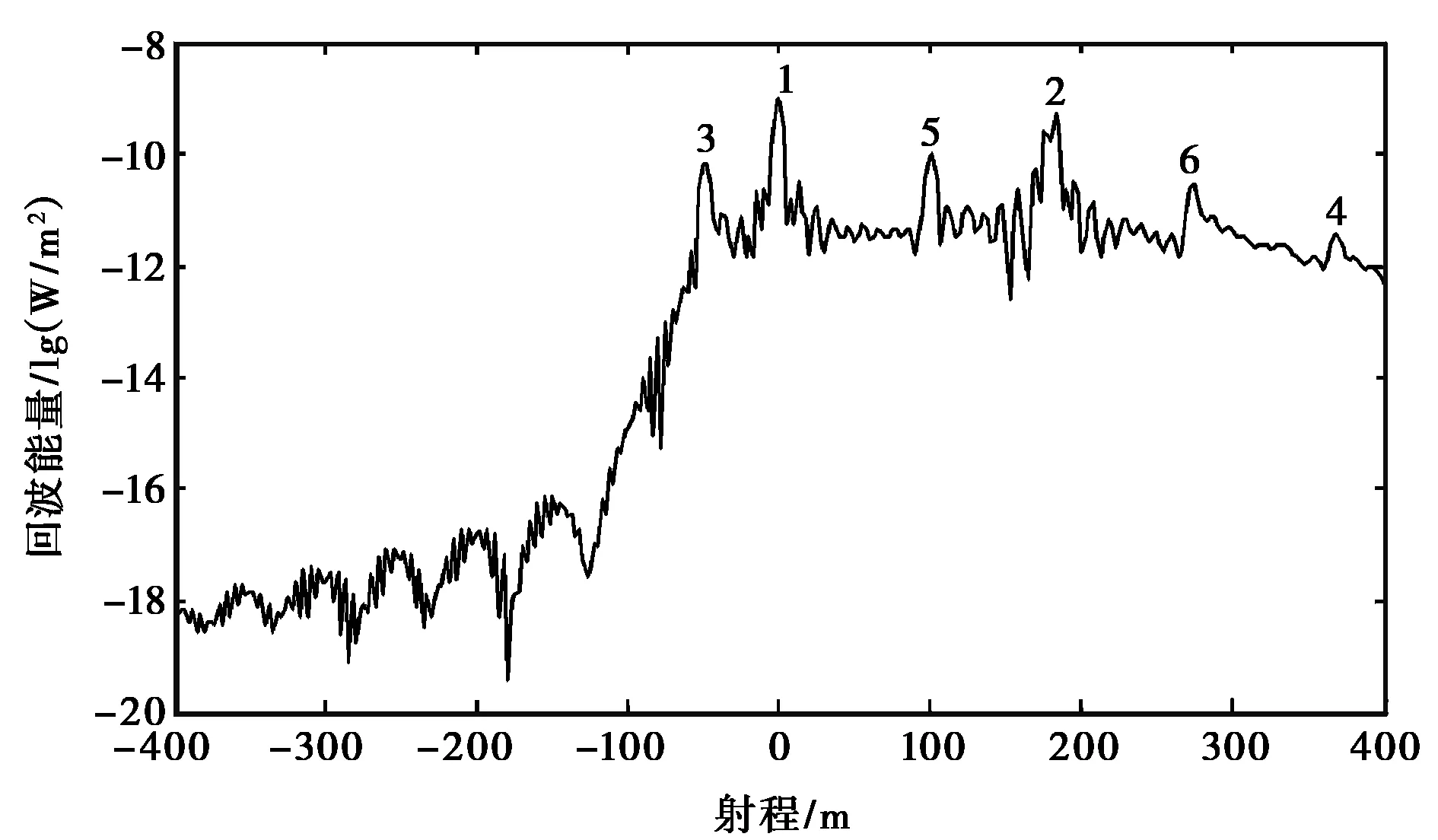
图9 山体倾斜度对雷达回波影响

3 结 论

本文详细分析了雷达参数和冰川模型参数对散射回波的影响,数值仿真数据对雷达实际测得数据可以做很好的解释,对设计雷达系统具有指导作用. 同时数值仿真数据可以帮助设计雷达信号处理算法和验证算法的正确性. 主要结论有:

1) 次表面散射场强度随着其粗糙度的增加而减小,粗糙度越大,减小的幅度也越大;

2) 表层粗糙度很小时,次表层更能分辨出来,但是随着表层粗糙度增加,非天底点回波能量增加,淹没次表层的回波,无法分辨次表层回波;

3) 随着带宽的增加,雷达探测仪距离向分辨率变大,能更好地观测冰川表面的细节特征,但是带宽的增加,必然要求中心频率的增加,这样会使雷达探测深度减小,所以要根据实际需要权衡带宽和中心频率的选择;

4) 不同山体倾斜度表现为回波时延不同,对雷达次表层的探测回波产生影响．

本文的机载正下视SAR回波模拟方法可以应用到多分层粗糙面媒质、多维度、高阶多次散射雷达回波数值模拟. 该数值仿真算法也可以应用到星体地下结构的探测[11-12].

[1] KOBAYASHI T,OYA H, ONO T. A-scope analysis subsurface radar sounding of Lunar mare region[J]. Earth planets space, 2002, 54(10): 973-982.

[2] KONG J A. Electromagnetic wave theory[M]. Cambridge: EMW Publication, 2000.

[3] PICARDI G, BICCARI D, SEU R, et al. Performance and surface scattering models for the Mars advanced radar for subsurface and ionosphere sounding (MARSIS)[J]. Planetary and space science, 2004, 52(1): 149-156.

[4] 郑宇腾, 赵延文, 贾苗苗,等. 求解多尺度目标电磁散射的积分方程快速算法[J]. 电波科学学报, 2014, 29(4): 601-605.

ZHENG Y T, ZHAO Y W, JIA M M, et al. Fast method for solving electromagnetic scattering from multiscale targets with integral equation[J]. Chinese journal of radio science, 2014, 29(4):601-605. (in Chinese)

[5] NOUVEL J F, HERIQUE A, KOFMAN W, et al. Radar signal simulation: surface modeling with the facet method[J]. Radio science, 2004, 39(1): RS1013.

[6] ULABY F T, MOORE R K, FUNG A K. Microwave remote sensing active and passive-volume II: radar remote sensing and surface scattering and emission theory[M]. Massachusetts: Addison-Wesley, 1982.

[7] 贾丽, 贾鑫, 许小剑, 等. 机场场景 SAR 原始数据模拟[J]. 雷达学报, 2014, 3(5): 565-573.

JIA L, JIA X, XU X J, et al. SAR raw data generation for complex airport scenes[J]. Journal of radars, 2014, 3(5): 565-573. (in Chinese)

[8] LI J L, PADEN J, LEUSCHEN C, et al. High-altitude radar measurements of ice thickness over the Antarctic and Greenland ice sheets as a part of operation icebridge[J]. IEEE transactions on geoscience remote sensing, 2013, 51(2): 742-754.

[9] ADRIAN K F. Microwave scattering and emission models and their applications[M]. London: Artech House, 1994.

[10]ONO T, OYA H. Lunar radar sounder (LRS) experiment on-board the SELENE spacecraft[J]. Earth planets space, 2000, 52(9): 629-637.

[11] ONO T, KUMAMOTO A, NAKAGAWA H, et al. Lunar radar sounder observations of subsurface layers under the nearside maria of the Moon[J]. Science, 2009, 323(5916): 909-912.

[12] PICARDI G, PLAUT J J, BICCARI D, et al. Radar soundings of the subsurface of Mars[J]. Science, 2005, 310(5756): 1925-1928.作者简介

吴超 (1987-),男,陕西人,博士研究生,研究方向为雷达SAR回波信号数值模拟、数字信号处理、全极化雷达遥感理论建模和反演及成像.

张晓娟 (1965-),女,山西人,研究员,博士生导师,研究方向为微波成像新技术、正向与逆向遥感理论、电磁场理论、计算电磁学.

方广有 (1964-),男,河南人,研究员,博士生导师,中国科学院电子学研究所副所长,研究方向为超宽带雷达系统、测月雷达、电磁场理论、太赫兹成像、地球物理探测方法.

Airborne 3D nadir-looking SAR echo numerical simulations for radar depth sounding of fast outlet glaciers and ice-sheet margins

WU Chao1,2ZHANG Xiaojuan2FANG Guangyou2

(1.University of Chinese Academy of Sciences, Beijing 100039, China;2.InstituteofElectronics,ChineseAcademyofSciences,Beijing100190,China)

A physical model for electromagnetic (EM) scattering from layered structure with multilayer rough interfaces is established, and the analytical expressions of radar observations are derived based on Kirchhoff approximation (KA) of rough surface scattering and the ray tracing of geometric optics (GO) theory, an efficient and accurate radar echoes simulator for airborne nadir-looking synthetic aperture radar (SAR) radar depth sounding of ice-sheet is developed for analyzing and processing the real radar observations. The radar signal simulator can be utilized to optimize the radar system design and improve radar data processing techniques, which can also be utilized to investigate subsurface structures in planetary exploration. The proposed radar signal numerical simulation method is validated with analytical expressions. With the different simulation configurations and system parameters, the scattering radar echo is simulated numerically by employing our proposed method, furthermore, the influence of ice surface roughness, subsurface roughness, the slopes of mountains, ice depth are investigated and the parameters of radar system on EM scattering fields, and the clear physical scattering meanings are provided. The proposed me thod can be utilized to calculate the radar echoes from layered structure with arbitrary roughness and geological topography property.

synthetic aperture radar (SAR); SAR echo simulations; inhomogeneous layered mediums; random rough surfaces scattering; Kirchhoff theory

10.13443/j.cjors.2015072202

2015-07-22

国家863计划项目(2012AA121901)； 国家自然科学基金(61172017,60890071)

TN955

A

1005-0388(2016)03-0494-08

吴超, 张晓娟, 方广有. 机载正下视SAR探测极地冰川的回波数值模拟[J]. 电波科学学报,2016,31(3):494-500+536.

WU C, ZHANG X J, FANG G Y. Airborne 3D nadir-looking SAR echo numerical simulations for radar depth sounding of fast outlet glaciers and ice-sheet margins[J]. Chinese journal of radio science,2016,31(3):494-500+536. (in Chinese). DOI: 10.13443/j.cjors.2015072202

联系人： 吴超 E-mail:wuchao211@mails.ucas.ac.cn