分布“可扩展数据流连接算法

王晓桐,房俊华,张蓉

(华东师范大学数据科学与工程研究院上海高可信计算重点实验室,上海200062)

分布“可扩展数据流连接算法

王晓桐,房俊华,张蓉

(华东师范大学数据科学与工程研究院上海高可信计算重点实验室,上海200062)

Join-Matrix是一种高性能的连接矩阵模型,方B部署于分布式环境下,支持任意连接谓词的数据流连接操作.由于采取随机分发元组作为路由策略,Join-Matrix可利用对元组内容的不敏感性来有效抵御数据倾斜.为了实现工作节点的负载均衡以及网络传输代价的最小化,基于连接矩阵模型设计一种高效的数据划分方案尤为重要.针对数据流连接处理,本文设计并实现了一种新颖的连接算子,可灵活地进行划分方案的自适应调整,以应对实时动态变化的数据分布.具体来说,我们根据数据流流量的采样信息和系统额定负载,通过一个轻量级的决策器制定出一个数据划分方案和相应的数据迁移计划,在保证输出结果完整性与正确性的情况下,实现迁移代价的最小化.本文在多种不同的数据集上进行了大量对比实验,结果证明,在资源利用率、系统吞吐率与时间延迟等方面,该连接算子较对比系统具有更高的性能体现.

数据流连接;Join-Matrix;数据划分;分布式计算

0 引言

随着在线实时分析连续数据流的需求日益增多,处理时刻变化数据流的新型应用越来越普遍,包括传感器网络、金融数据在线分析和网络入侵检测等.诸如此类的应用具有以下特征:①在海量数据上执行包含复杂谓词的连接操作;②在保持高效率和快速响应时间的同时进行实时数据分析;③需要维持大量依赖于历史数据的状态信息.因此,为了提高数据流系统的处理性能,设计高效的数据流连接算法尤为重要.

研究者对数据流连接算法已投入了大量相关的研究工作,提出了若干集中式连接算法[1-3].这些连接算法均在一个中心节点对数据流进行连接处理,不能高效处理数据量巨大的流式数据.由于目前主流的数据流处理系统均是分布式的,将连接操作分布式处理更符合数据流系统的特点.因此分布式数据流连接算法应运而生.大多数分布式连接算法主要针对等值连接,处理高选择性的θ连接性能欠佳.除此之外,分布式算法大多采用哈希函数进行数据划分,对数据内容的不敏感性导致不能灵活地进行系统结构的扩展.

本文的主要研究目标是基于连接矩阵模型,设计并实现一种新颖的分布式数据流连接算法,旨在提高连接矩阵的可扩展性与灵活性,从以下两方面实现:①探索适当的数据划分方案,以充分利用系统资源;②设计高效的状态重分配和数据路由策略,以降低自适应调整代价和网络传输开销.文献［4］指出目前已有的自适应技术只依赖于启发式模型,缺乏理论证明.本文继承了传统数据划分方案的特性,并提出了相应的改进措施.

本文的主要贡献是:①基于连接矩阵设计一种高效的数据划分方案,打破节点个数的规整性限制,可根据数据动态分布灵活地增删物理计算节点,提高系统架构的可扩展性与灵活性;②频繁进行自适应调整的策略会导致巨大的网络传输成本,而保守策略不能根据数据动态变化进行自适应调整,从而降低系统的处理性能.为了在二者之间达到平衡,本文提出一个在线算法,高效地决定何时探索和触发新的划分方案;③提出一种统一的、位置感知的迁移机制,实现迁移代价的最小化;④传统的自适应技术[5-6]以阻塞方式进行状态数据重分配,本文以非阻塞的方式在进行数据迁移的同时处理新流入的元组;⑤通过在多种不同数据集上的大量对比实验证明,本文提出的连接算子具有良好的性能.

1 相关工作

近年来,研究人员利用Join-Matrix矩阵模型进行分布式连接查询处理,在类似MapReduce的系统与数据流系统均有涉足.Join-Matrix模型将两个数据集间的连接操作建模成一个矩阵,矩阵的每一条边分别代表一个数据集,每个矩阵单元代表一个潜在的连接输出结果. Stomos等人在文献［7］中首次引进连接矩阵的概念,在FR算法[8]的基础上提出了“对称片段与复制”算法(symmetric fragment and replicate),以解决FR算法带来的计算代价与通信代价庞大的问题.在MapReduce的编程框架下,文献［9］基于连接矩阵提出了两种数据划分方案,分别是1-Bucket与M-Bucket.1-Bucket采取随机分发元组的路由策略,即内容不敏感,在输出结果方面可以很好地实现负载均衡,但由于过多地输入元组复制存储,在处理低选择性的连接操作时性能欠佳.另一方面,M-Bucket根据输入元组的内容进行数据划分,即内容敏感,尽管解决了元组冗余存储的问题,但可能导致某些计算节点出现过载的现象.

与本文设计思路最相似的研究是Elseidy等人提出的Dynamic连接算子[10].Dynamic连接算子采用“网格划分方案”将连接矩阵划分成2n(n∈N*)个面积相等的区域,并采用随机路由策略分发输入元组.由于要维持矩阵的结构特性,当架构需要进行扩展或缩减时,必须同时增加或删除一行或一列的所有处理单元,由此引发迁移代价的剧增和资源利用率的降低,算子结构的灵活性与可扩展性也深受影响.为了解决这个问题,本文设计了一种更为灵活的数据划分方案,达到更好的效果.

2 连接算子

2.1 预备知识

Join-Matrix以矩阵的形式处理R▷◁S,矩阵的每一条边代表一条数据流,矩阵单元代表潜在的连接输出结果.如图1(a)所示,在连接矩阵中进行不等值连接操作,图中的数字代表连接属性,7色的单元格代表符合连接谓词的输出结果.基于连接矩阵M的数据划分方案将矩阵切分成n×m个面积相等的处理单元Cij,每个处理单元分配一台物理计算节点,并存储数据流的子集〈Ri,Sj〉,其中i∈［0,n一1］,j∈［0,m一1］,并用［b,e］代表子数据集对于数据流的位置范围.如图1(b)所示,将图1(a)中的矩阵切分成2×4个处理单元,每个处理单元分别存储1/2的R流数据和1/4的S流数据.

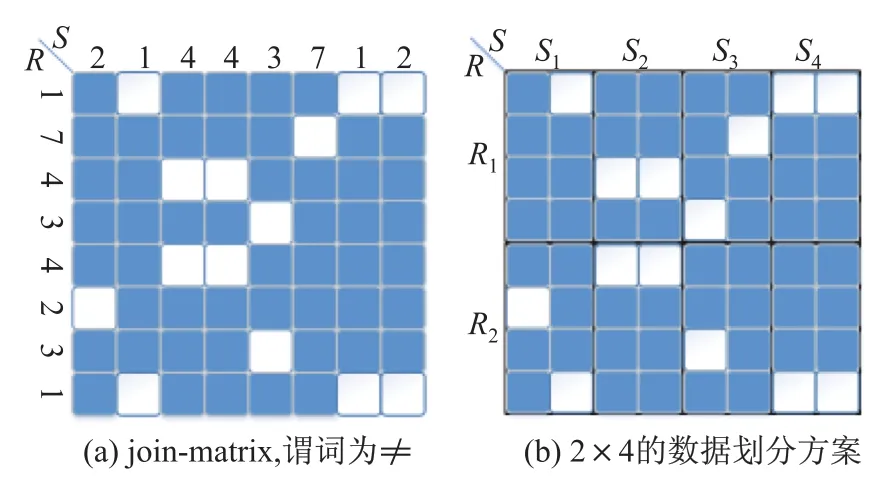
图1 连接矩阵及划分方案示例Fig.1Example of join-matrix and partitioning scheme

处理θ连接操作的代价主要与系统的内存开销、CPU计算成本以及网络通信代价有关,其中CPU的计算成本与连接矩阵的计算区域面积|R|·|S|成正比(|R|和|S|分别代表两条数据流的流量,即元组的数量),与选取的数据划分方案无关,即独立于矩阵的行数n和列数m.根据文献［10］,内存开销与单个处理单元的半周长|Ri|+|Sj|成比例,而|Ri|+|Sj|取决于矩阵的行数与列数.对于网络通信代价同样成立.因此,本文旨在寻求合适的数据划分方案n×m,使得系统的资源使用量最低.假设单个处理单元的额定内存大小为V,则本文的目标可以形式化定义成以下优化问题:

2.2 划分方案

由于连接矩阵的行数与列数决定了内存开销,关于矩阵的面积与周长,我们已知两个常识:①给定面积的所有矩阵中,正方形的周长最小;②给定周长的所有矩阵中,正方形的面积最大.基于上述常识,我们得出以下定理.

证明首先假设单个处理单元的CPU计算资源为定值,为了确保两条流的任意元组均可相遇,则R▷◁S的计算复杂度为O(|R|·|S|).当时,系统的内存使用量最小;其次假设单个处理单元的内存空间是定值,当时,连接矩阵使用的处理单元总数最小.由于网络传输代价与内存开销相关,因此定理1成立.

根据定理1,如果数据流流量|R|和|S|均可被Vh整除,则由此生成的数据划分方案是最优的.但是大多数情况下,数据流流量不能被Vh整除,考虑到矩阵的行数与列数必须为整数,我们令,则连接矩阵使用的处理单元总数N为:

由于数据流流量不能被Vh整除,在装载输入元组的过程中,矩阵最后一行或者一列的处理单元中会产生数据碎片,我们称这些处理单元为“碎片单元”.我们假设V=8 GB,|R|= 9 GB,|S|=9 GB,则R▷◁S对应的计算区域如图1(a)所示.根据公式(2),将矩阵划分成9个处理单元,各个处理单元存储数据的情况分别是C00=〈4 GB,4 GB〉,C01=〈4 GB,4 GB〉, C02=〈4 GB,1 GB〉,C10=〈4 GB,4 GB〉,C11=〈4 GB,4 GB〉,C12=〈4 GB,1 GB〉,C20=〈1 GB,4 GB〉,C21=〈1 GB,4 GB〉,C22=〈1 GB,1 GB〉.显然,C02、C12、C20、C21和C22均为碎片单元,因为存储的R流和S流数据总量低于额定内存空间.

图2 数据划分方案Fig.2Partitioning scheme

为了充分利用系统资源,实现处理单元之间的负载均衡十分重要.我们将两条数据流定义为主流P和副流D以作区分.主流P可以为数据流R或者S.首先保证主流P的元组数据分配到足够的内存空间,将P切分成Pγ个子集分发到处理单元中;其次将单个处理单元中剩余的内存分配给副流D的元组数据,则划分副流D得到的子集个数.因此,处理单元总数N为:

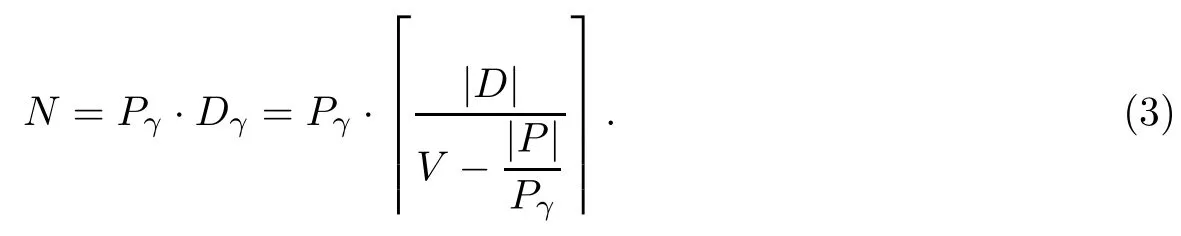
算法1阐述了基于连接矩阵制定数据划分方案的具体过程.首先,将Pγ中的四个元素依次代入等式(3)计算出对应的处理单元个数Ni(i 6 4),选择值最小的Ni作为处理单元总数,并将对应的赋值给于Pγ和Dγ(第1～5行).其次根据主流P的流量和子集个数Pγ,计算出连接矩阵的行数n和列数m:如果,则数据流R为主流P,n=Pγ,m=Dγ;否则数据流S为主流P,m=Pγ,n=Dγ(第6～10行).

2.3 迁移计划

在进行划分方案的切换之前,需要先确定新旧矩阵中处理单元的对应关系.假设Cij和Ckl分别是旧矩阵M0和新矩阵Mn中的处理单元,我们利用一个相关系数来衡量两个处理单元Cij和Ckl之间数据集重叠度,给出如下定义:

给定矩阵M0和Mn,定义处理单元之间的关系映射条目.更新处理单元映射关系表可分为两步骤:①枚举出所有可能的npi;②选取值最大的npi作为最终条目插入到关系映射表NP.

迁移计划决定了矩阵变换期间数据是如何在处理单元之间重新分配的.为了方B描述,下面我们将只讨论R流的数据迁移,对于S流采取类似的操作.我们将需要迁入处理单元Ckl的 R流数据集定义如下:

图3 数据迁移示例Fig.3Example of data migration

3 实验

3.1 实验环境

实验设备:22个处理节点的刀片机服务器集群,单个节点有2个四核四线程处理器,型号为Intel Xeon E5335,主频2.00 GHZ,并配有共计16 GB的RAM以及2 TB的硬盘.所有节点运行CentOS 6.5 Linux操作系统,Apache Storm 0.10.0[12]以及Java 1.7.0.

数据集:使用TPC-benchmark[13]的数据生成器dbgen生成不同规模的数据集.我们对这些数据集进行预处理,即将其调整为在连接属性上具有Zipf分布的形式,通过参数z调整数据倾斜程度,默认情况下,我们将数据集的倾斜度设置为1.

查询语句:我们使用［10］中的等值查询语句EQ5和范围查询语句BNCI.其中EQ5是［10］重定义的TPC-H中Q5查询中代价较高的几个连接谓词组成的查询语句;BNCI是按照某一属性范围查找其在另一个数据集中的匹配记录.

3.2 评估指标

我们将通过以下四个指标对系统的资源利用率和处理性能进行评估:①处理单元数:系统运行过程中,连接算子使用到的处理单元的总数,单个处理单元分配额定大小的内存空间;②吞吐率:单位时间内系统成功接收并处理的元组数量;③迁移量:新旧连接矩阵进行转换期间,需要拷贝和移动的元组总量;④计划耗时:根据当前系统的工作负载制定数据划分方案、更新单元映射表以及生成迁移计划的总耗时.

3.3 对比系统

我们使用了三种不同的连接算子来进行对比实验:①MFM.本文提出的自适应连接算子,根据等式3计算出最优的连接矩阵及数据划分方案;②Dynamic.文献［10］设计的连接算子,限制连接矩阵个数必须为2的幂次方个,以单个处理单元×4的形式进行矩阵的扩展;③Readj.文献［11］设计的连接算子,以key为粒度,通过一个哈希函数重新调整各处理单元的工作负载以实现负载均衡.

3.4 结果与分析

实验在全历史模式下进行,并通过调整输入数据的倾斜度验证连接算法的灵活性和自适应性.设置V=8·105,并连续地将6·106条元组数据装载入系统中.图4展示了执行BNCI时处理单元数与迁移代价的变化趋势.随着数据的不断流入,Dynamic算子占用的处理单元数大幅度递增,导致消耗的内存空间也急剧增加.相反,MFM根据当前系统的负载情况按需分配资源,占用的处理单元数远远少于Dynamic.相应地,为了维持连接矩阵的结构特性,Dynamic需要进行大规模的数据备份;而MFM算子使用较少的处理单元数,充分利用系统资源.因此, Dynamic算子在数据迁移期间产生的迁移代价远远超过MFM.

图4 BNCI无窗口模式Fig.4Full-history join with BNCI

图5 EQ5全历史模式Fig.5Full-history join with EQ5

为了保证系统的负载均衡,对于单个处理单元和单位时间间隔t,定义均衡度标识,其中为所有处理单元的平均负载.在本组实验中,执行查询语句EQ5,并设置θt6 0.05.如图5(a)所示,Readj的计划耗时高于其余两种连接算子三个数量级.究其原因可知, Readj通过一个哈希函数调整所有处理单元中的工作负载,因此在进行扩容操作时,Readj需要重新计算全局的均衡状态,而其余两种连接算子均采用内容不敏感性的随机路由策略,无需进行平衡调度.图5(b)给出了三种连接算子在不同数据倾斜程度下的吞吐率.一方面,随着倾斜参数的递增,由于计划耗时长,Readj的吞吐率呈现递减趋势.另一方面,尽管Dynamic连接算子占用的处理单元远多于MFM,但是由于其庞大的数据迁移量,MFM的吞吐率略高.

4 总结

为在数据流系统上高效地执行分布式θ连接操作,本文基于连接矩阵模型提出可灵活地进行自适应调整的连接算法,利用对其内容不敏感性抵御数据倾斜,根据当前系统负载按需分配资源,采用非阻塞的方式处理数据迁移并保证连接结果的完整性与正确性.实验证明,对比目前已有的连接算法,本文提出的连接算法性能更为优越且稳定.未来的工作将会考虑对连接矩阵模型进一步优化,打破矩阵单元个数规整性的限制以实现更为优良的性能.

［1］DITTRICH J-P,SEEGER B,TAYLOR D S,et al.Progressive merge join:A generic and non-blocking sort-based join algorithm[C]//Proceedings of the 28th VLDB Conference.2002:299-310.

［2］URHAN T,FRANKLIN M J.XJoin:A reactively-scheduled pipelined join operator[J].IEEE Data Eng Bull, 2000,23(2):27-33.

［3］WANG S,RUNDENSTEINER E.Scalable stream join processing with expensive predicates:Workload distribution and adaptation by time-slicing[C]//Proceedings of the 12th Conference on EDBT.2009:299-310.

［4］GOUNARIS A,TSAMOURA E,MANOLOPOULOS Y.Adaptive query processing in distributed settings[J]. Intelligent Systems Reference Library,2013,36:211-236.

［5］LIU B,JBANTOVA M,RUNDENSTEINER E A.Optimizing state-intensive non-blocking queries using run-time adaptation[C]//Proceedings of the 2007 IEEE 23rd ICDEW.IEEE,2007:614-623.

［6］PATON N W,BUENABAD-CHAVEZ J,CHEN M,et al.Autonomic query parallelization using non-dedicated computers:An evaluation of adaptivity options[J].The VLDB Journal,2009,18(1):119-140.

［7］STAMOS J W,YOUNG H C.A symmetric fragment and replicate algorithm for distributed joins[J].IEEE Transactions on Parallel&Distributed Systems,1993,4(12):1345-1354.

［8］EPSTEIN R,STONEBRAKER M,WONG E.Distributed query processing in a relational data base system [C]//Proceedings of ACM SIGMOD Conference on Management of Data.1978:169-180.

［9］OKCAN A,RIEDEWALD M.Processing theta-joins using MapReduce[C]//Proceedings of ACM SIGMOD Conference on Management of Data.2011:949-960.

［10］ELSEIDY M,ELGUINDY A.Scalable and adaptive online joins[J].The VLDB Endowment,2014,7(6):441-452.

［11］GEDIK B.Partitioning functions for stateful data parallelism in stream processing[J].The VLDB Journal,2013, 23(4):517-539.

［12］Apache storm[EB/OL].[2016-06-10].http://storm.apache.org.

［13］The TPC-H benchmark[EB/OL].[2016-06-10].http://www.tpc.org/tpch.

(责任编辑:林磊)

Distributed and scalable stream join algorithm

WANG Xiao-tong,FANG Jun-hua,ZHANG Rong
(Institute for Data Science and Engineering,Shanghai Key Laboratory of Trustworthy Computing,East China Normal University,Shanghai200062,China)

Join-Matrix is a high-performance model for stream join processing in a parallel shared-nothing environment,which supports arbitrary join operations and is resilient to data skew for taking random tuple distribution as its routing policy.To evenly distribute workload and minimize network communication cost,designing an efficient partitioning policy on the matrix is particularly essential.In this paper,we propose a novel stream join operator that continuously adjust its partitioning scheme to real-time data dynamics.Specifically,based on the sample statistics of streams and rated load of each physical machine,a lightweight scheme generator produces a partitioning scheme; then the corresponding solutions for state relocation are generated by a migration plan generator to minimize migration cost while ensuring result correctness.Our experiments on different kinds of data sets demonstrate that our operator outperforms the static-of-the-artstrategies in resource utilization,throughput and system latency.

stream join processing;Join-Matrix;partitioning scheme;distributed computing

TP391

A

10.3969/j.issn.1000-5641.2016.05.010

1000-5641(2016)05-0081-08

2016-05

国家863计划项目(2015AA015307)；国家自然科学基金重点项目(61232002,61332006);国家自然科学基金(61432006)

王晓桐,女,硕士研究生,研究方向为数据流处理.E-mail:51164500121@stu.ecnu.edu.cn.

张蓉,女,博士,副教授,研究方向为分布式数据管理.E-mail:rzhang@sei.ecnu.edu.cn.