温度对介电弹性体材料致动器动态性能的影响

盛俊杰， 张玉庆， 李树勇， 陈花铃

(1.中国工程物理研究院总体工程研究所， 四川绵阳621900； 2.西安交通大学机械工程学院， 西安710049；3. 机械结构强度与振动国家重点实验室， 西安710049)



温度对介电弹性体材料致动器动态性能的影响

盛俊杰1， 张玉庆1， 李树勇1， 陈花铃2，3

(1.中国工程物理研究院总体工程研究所， 四川绵阳621900； 2.西安交通大学机械工程学院， 西安710049；3. 机械结构强度与振动国家重点实验室， 西安710049)

介电弹性体材料(Dielectric Elastomer，简称DE)具有很强的粘弹性，由于DE材料的粘弹性具有时间依赖关系，从而使其应力-应变也具有时间依赖性，因此动态变形中，其能量转换、宏观变形等特性也必然受到粘弹性的影响。同时，DE的粘弹性和介电常数具有很强的温度依赖性。通过引入温度对介电常数、弹性模量和粘弹性松弛的影响，并结合DE的粘弹性力学模型和欧拉-拉格朗日方程，构建了不同环境温度场下的DE系统的动力学控制方程。最后，通过数值模拟，分析了温度对DE材料致动器动态性能的影响。研究结果能为DE致动器的结构设计和动态变形控制提供理论指导。

介电弹性体材料；动态性能；温度

引言

介电弹性体材料(Dielectric Elastomer，简称DE)是一种新型的智能电活性聚合物(Electroactive Polymer，简称EAP)。相比于其他EAP材料，DE材料独有的特点是变形大、弹性模量低、机电耦合效率高、工作温度范围宽和频率范围广(0.1～20 kHz)。DE致动器指的是在DE材料上下表面涂有柔性电极的三明治结构，在电极上施加电压后，DE材料上产生的Maxwell电场力和电致伸缩电应力的共同作用挤压材料，结果使其面积增大、厚度减小，并逐渐成为近几年国内外的研究热点之一[1-3]。近年来，研究学者设计出很多种基于DE材料的致动器和换能器结构，并尝试将DE应用于航空航天、医学与智能机器人等领域[2-3]。

在工程实际应用中，对DE材料施加的载荷常常是周期性的电压或者应力，如微泵结构、各种运动驱动器、能量循环收集器等[3]，然而现有研究对DE材料在交变载荷下的动力学变形行为以及力电耦合特性的研究尚没有得到足够的重视。近两年来，学者们才开始了对DE材料动态特性的研究。哈佛大学的Zhu从热动力学出发，通过扰动方法研究了DE气球[4]的非线性振动特性；兰州大学的Yong等人[5]建立了一套DE动态分析模型，研究了厚球壳的稳定性；浙江大学的Li[6]研究了纯剪切共振器的力电耦合性能及其动态性能；Federal University of Goiás的Soares等[7]利用打靶法对预拉伸后的超弹性平面薄膜的动态方程进行了求解，并与有限元求解方法进行了对比；最近TU Darmstadt的Xu[8]利用拉格朗日方程得到了平面DE的动态运动方程，并研究了动态载荷下的位移响应和稳定性，但是没有考虑预应力的影响。

由于DE材料的粘弹特性具有时间依赖关系，从而使其应力-应变也具有时间依赖性，因此动态变形中，其能量转换、宏观变形等特性也必然受到粘弹性的影响。但在现有的研究中，关于DE材料交变电场作用下受粘弹性影响的应变能及电能的转换规律对DE材料的动态变形及稳定性影响等缺少研究。同时，温度会在很大程度上影响DE材料的粘弹性松弛，而温度又会对DE材料的力学性能和介电性能产生影响，因此温度也会对粘弹性DE材料的动态性能产生影响。

从欧拉-拉格朗日方程出发，结合DE材料的粘弹性力学模型，得到了平面粘弹性DE材料致动器试件的动力学运动控制方程。最后，通过得到的控制方程，分析了温度对DE材料致动器动态性能的影响。

1DE致动器的动力学方程

1.1欧拉-拉格朗日方程

DE致动器是在DE材料的上下两面涂上柔性电极后的一种三明治结构，施加电压Φ后，DE材料的上、下表面积累了一定的电荷±Q，电荷之间产生的Maxwell电场力和电致伸缩电应力的共同作用挤压材料，结果使其面积增大、厚度减小。

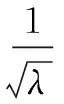
图1DE致动器的工作原理图

假设DE致动器的中心位置在振动过程中没有变化，即中心点的坐标一直为(0,0,0)，在动态电场作用下DE致动器的变形是时间的函数λ(t)，那么可以得出致动位置和参考位置在整个坐标系中的关系式：

(1)

DE致动器系统的欧拉-拉格朗日方程可以写为：

(2)

式中：L为拉格朗日函数；K为DE系统的动能(单位：J)；U为DE系统的势能(单位：J)。

1.2DE系统的动能和势能

DE系统的动能K可以表示为[8]：

(3)

式中：ρ为材料密度(单位：kg·m-3)。

DE系统的势能是系统的自由能密度函数对体积的积分，而系统的自由能包含两个方面，Helmholtz自由能和电势能[9]。

此刻，丁达的身体被一层泡泡包裹着，这原本是困住宴西园的泡泡。原来，在喵星飞鼠大使发射导弹的这几秒内，壶天晓条件反射般地把原本包裹着宴西园的泡泡罩在了丁达体外。壶天晓和镜心羽衣一个采集原料，一个织补泡泡，这一切都在瞬间完成，像是没经过大脑指挥似的，连他们自己都惊讶不已。不过，导弹爆炸的冲击力仍然在防护泡上炸开一个大洞，在丁达的后背上留下爆燃后的烧灼痕迹。过了好一会儿，泡泡上的大洞才逐渐愈合。或许是出于对云织、猎影星族的恐惧，喵星飞鼠大使愣在那里，不敢轻举妄动了。

作为一种同时具有弹性和粘性的DE材料，在变形的过程中必然会产生粘弹性松弛。DE材料的粘弹性可用一系列的弹簧和阻尼来进行描述，即所谓的流变模型[10-11]，如图2所示。流变模型由两部分组成：网链A是一个弹簧，用来表征超弹性的可逆变形；网链B由一个弹簧和一个粘壶串联组成的Maxwell模型，用来表征不可逆的非弹性变形。在这种Maxwell模型中，网链B所承受的应力和粘壶应力相等，体系总的应力为两个网链的应力之和，体系的总应变为两个网链应变之积。

图2DE材料的粘弹性模型

由于在研究DE材料致动器的动力学特性时，其在平衡位置附近的变形不大，不需要考虑大变形下的应变刚化现象，所以，我们采用Neo-Hookean模型来表示DE致动器系统弹性应变能，于是，系统的自由能为：

(4)

式中：μA(T)为A弹簧的剪切模量(单位：Pa)；μB(T)为B弹簧的剪切模量(单位：Pa)；ξ为粘壶的变形量；c0为材料的比热(单位：J·K-1·kg-1)；T为绝对温度(单位：K)；T0为参考温度(单位：K)；ε0εr(λ,T)=ε为DE材料的介电常数；ε0为真空介电常数，取值8.85×10-12F·m-1。εr(λ,T)是温度和变形的函数，可以表示为[12]：

b(2λ-2)2+c(2λ-2)3)

(5)

基于各向同性假设，可以得到DE材料致动器的势能：

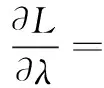
(6)

整理以上公式，得到DE系统的动力学控制微分方程：

(7)

(8)

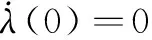
2温度对DE致动器动态性能的影响

温度不仅影响DE的介电常数和弹性模量，而且对DE的粘弹性松弛时间有很大的影响，因而必然会对DE致动器的动态性能产生一定的影响。

图3为不同温度下DE平面致动器的幅频响应曲线。由图可见，在T=295 K下，DE致动器的共振频率为405 Hz，此时的最大振幅为1.417；在T=305 K时，DE致动器在358 Hz时共振，其最大振幅为1.528；温度升高到315 K的时候，DE致动器在314 Hz下具有最大的振幅值1.618。也就是说，随着温度升高，DE致动器的共振频率下降，而最大振幅却在上升，这是因为温度升高使DE材料的弹性模量减小的缘故。

图3不同温度下DE材料的幅频响应曲线

图4为三种温度295 K、305 K和315 K下，DE致动器的总的应变比λ(图4中(a)、(c)、(e))和非弹性变形ξ(图4中(b)、(d)、(f))随时间的变化关系，其中电场激励频率f=330 Hz。在330 Hz下，当温度从295 K升高到315 K的时候，DE致动器的振动越来越剧烈，振幅越来越大，表现出周期性的振动特性；由于DE材料的松弛时间在几十秒的数量级，比电场变化周期大很多，因而此时的粘弹性松弛影响比较小，如图4(b)、图4 (d)和图4 (f)所示。

图4三种温度下DE致动器的总的变形和非弹性变形(330 Hz)

图5为295 K、305 K和315 K温度下粘弹性DE材

料的相平面图(图5(a)～图5(c))和庞加莱映射图(图5(d)～图5(f))。可以清晰地看出，激励频率f=330 Hz时，三种温度下的相位图均形成了封闭了曲线，同时，对应温度下的庞加莱映射图中的点集都有规律的分布在一条封闭环曲线上，代表着它们的运动是拟周期运动[14]。

3结束语

在欧拉-拉格朗日方程的基础上，研究了温度对DE系统非线性动态性能的影响，包括：幅频曲线、变形响应曲线和庞加莱映射图。温度升高后，系统的共振频率减小，最大振幅会增加。在295 K、305 K和315 K温度下，DE在共振频率附近的振动都是稳定的，同时温度升高后，滞后会越来越明显，此时具有比较明显的能量损耗产生。

在DE动力学运动控制方程中引入了粘弹性的影响，并考虑了温度对介电性能和力学性能的影响，借助建立的粘弹性运动控制方程，可以合理地对DE进行结构设计，有效地控制其振动变形、抑制其失效现象发生。因此，研究成果具有重要的实际应用价值。

图5不同温度下粘弹性DE材料的相平面图和Poincaré映射图(330 Hz)

[1] PELRINE R,KORNBLUH R,PEI Q,et al.High-speed electrically actuated elastomers with strain greater than 100%[J].Science,2000,287(5454):836-839.

[2] CARPI F,ROSSI D D,KORNBLUH R,et al.Dielectric elastomers as electromechanical transducers[M].Amsterdam:Elsevier,2008.

[3] BROCHU P,PEI Q.Advances in dielectric elastomers for actuators and artificial muscle[J].Macromolecular Rapid Communications,2010,31(1):10-36.

[4] ZHU J,CAI S,SUO Z.Nonlinear oscillation of a dielectric elastomer balloon[J].Polymer International,2010,59(3):378-383.

[5] YONG H,HE X,ZHOU Y.Dynamics of a thick-walled dielectric elastomer spherical shell[J].International Journal of Engineering Science,2011,49(8):792-800.

[6] LI T,QU S,YANG W.Electromechanical and dynamic analyses of tunable dielectric elastomer resonator[J].International Journal of Solids & Structures,2012,49(26):3754-3761.

[7] SOARES R M,GONCALVES P B.Nonlinear vibrations and instabilities of a stretched hyperelastic annular membrane[J].International Journal of Solids & Structures,2012,49(3-4):514-526.

[8] XU B X,MUELLER R,KLASSEN M,et al.Dynamic analysis of dielectric elastomer actuators[J].Applied Physics Letters,2012,11(1):935-938.

[9] SUO Z G.Theory of dielectric elastomer[J].Acta Mechanica Solida Sinica,2010,23(6):549-578.

[10] ZHAO X H,KOH S J A,SUO Z G.Nonequilibrium thermodynamics of dielectric elastomer[J].International Journal of Applied Mechanics,2011,3(2):203-217.

[11] FOO C C,CAI S,KOH S,et al.Model of dissipative dielectric elastomers[J].Journal of Applied Physics,2012,111(3):034102-034114.

[12] VU-CONG T,JEAN-MISTRAL C,SYLVESTRE A.New operating limits for applications with electroactive elastomer: Effect of the drift of the dielectric permittivity and the electrical breakdown[C]//Proceedings of SPIE-The International Society for Optical Engineering, Electroactive Polymer Actuators and Devices(EAPAD)2013,San Diego,California,USA,March 10-12,2013:793-806.

[13] SHENG J,CHEN H,LI B,et al.Nonlinear dynamic characteristics of a dielectric elastomer membrane undergoing in-plane deformation[J].Smart Materials & Structures,2014,23(4):494-501.

[14] 闻邦椿,李以农,徐培民.工程非线性振动[M].北京:科学出版社,2007.

Effect of Temperature on the Dynamic Performance of a Dielectric Elastomer Actuator

SHENGJunjie1,ZHANGYuqing1,LIShuyong1,CHENHualing2,3

(1.Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621900, China;2.School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China;3.State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an 710049, China)

Dielectric elastomers (DEs) have strong viscoelasticity. Because of their viscoelasticity, DEs are able to produce a large time dependent electromechanical deformation. In the current study, the Euler-Lagrange equation is used to characterize the influence of temperature on the dynamic electromechanical deformation by taking into account temperature dependent permittivity and elastic modulus of DE. Then, the numerical results are present to investigate the time-dependent dynamic performance, phase diagram, and Poincare’ map associated with the viscoelastic dissipative process. The dynamic response has strong temperature and frequency dependencies, which may guide the design of high-performance DE Actuator and the control of its dynamic deformation.

dielectric elastomer; dynamic performance; temperature

2016-03-27

国家自然科学基金项目(11402246)

盛俊杰(1986-),男,山东单县人,高级工程师,博士,主要从事智能材料与结构方面的研究,(E-mail)scu2005sjj@163.com;

陈花铃(1954-),女,陕西韩城人,教授,博导,博士,主要从事智能材料与结构、机械振动与噪声控制理论与技术方面的研究,(E-mail)hlchen@mail.xjtu.edu.cn

1673-1549(2016)04-0016-05

10.11863/j.suse.2016.04.04

TB381;TB122

A