带有一个无优先权冷贮备部件的Birolini双 部件系统可靠性分析

黄凯,吴清太

(南京农业大学理学院,南京210095)

带有一个无优先权冷贮备部件的Birolini双 部件系统可靠性分析

黄凯,吴清太

(南京农业大学理学院,南京210095)

研究了两个同型主部件组成的Birolini系统,并带有一个无优先权的冷贮备备用部件组成的三部件可修系统.假定部件的寿命服从指数分布、部件的修理时间服从一般连续型分布,通过补充变量法和广义马尔可夫过程方法,得到了系统可靠度的Lap lace变换、首次故障前平均时间、稳态可用度与稳态故障频度等重要可靠性指标.

优先权;Birolini双部件系统;可靠度;广义马尔可夫过程

0 引言

现代机械设备越来越复杂,而且一旦发生故障所造成的损失以及对人类安全和环境的危害变得不再无足轻重,例如医院或核电站的发电机发生故障其损失将难以估计.因此人类社会更加关注机械设备的可靠性、安全性.而贮备系统对可修系统模型的可用度、可靠性以及系统的安全性有了很大的提升［1-3］.常用的一种贮备模型为冷贮备.冷贮备的概念为,一个贮备系统以零故障率被保持贮备直至可修复的运行系统出现故障［4-7］.另一种常用的贮备模型为温贮备.温贮备的概念为,部件在贮备期的无故障时间随机大于部件工作状态时的无故障时间.如文献［8］中分析的Birolini双部件系统就由一个运行部件、一个同型温贮备部件及一个修理工组成,当运行部件失效则温贮备部件立即转到运行状态,此时转到运行状态的部件的失效率也由λw转入部件运行时的失效率λ,值得注意的是λw＜λ.Birolini双部件系统是一个封闭式循环系统,当修理工空闲时,任何部件的失效修理工都会马上对失效部件进行修理;当失效部件修理完成后,若正在运行的部件没有失效则修好的部件进入温贮备状态,否则修理完成的部件直接进入运行状态.

贮备系统通常被赋予了优先权规则,即主部件比贮备部件有优先使用权或失效后有优先修理权.在实际生活中,这种带优先权的贮备系统也应用广泛.例如,在医院的手术室内,在手术过程中,若国家电力供应系统突然发生故障,若手术因此而不得不停止,这将对躺在手术台上的病人造成非常严重的后果,故手术室内通常都会有备用供电系统以保证手术顺利进行.由于国家电力供应系统无论是在安全性方面还是在费用方面都比本地备用供电系统更值得使用,所以国家电力供应系统就比备用供电系统有优先使用权,一旦国家电力供应系统恢复正常,备用系统就将不再使用而进入贮备状态.近些年来带有优先权的可修贮备系统得到了很多关注［9-10］.

基于以上文献研究的两部件系统,本文研究了两同型主部件组成的Birolini系统,并附有一个无优先权的备用部件组成的三部件系统,且主部件对备用部件有优先使用权.系统开始运行时,主部件运行,同型主部件处于温贮备状态,备用部件处于冷贮备状态.本文假定部件工作时间服从指数分布、修理时间服从一般连续分布,利用马尔可夫过程理论和Laplace变换的方法,求出了系统可靠度的Lap lace变换式和首次故障前平均时间的表达式,以及系统的稳态可用度和稳态故障频度等可靠性指标.此外,还通过数值模拟分析了系统参数对系统可靠性的影响.

1 模型假设

假设1系统由两个同型主部件的Birolini系统及一个备用部件组成的三部件运行,且有一个修理工.

假设2系统工作时,主部件运行,另一主部件处于温贮备状态,而备用部件处于冷贮备状态.

假设3设主部件的运行的失效率为λ,主部件温贮备的失效率为λw,备用部件运行的失效率为λs.

假设4当主部件运行失效,若处于温贮备状态的主部件没有失效,则立刻加以替换,失效率由λw转换成λ,同时修理工立即对失效主部件进行维修,且修复如新;否则备用部件立刻运行,失效主部件等待维修.部件间的转换是瞬时完成的.

假设5当主部件维修完成,若另一主部件正在运行,则完成维修的主部件进入温贮备状态;否则修复好的主部件立刻运行,备用部件进入冷贮备状态.

假设6备用部件仅在两主部件都失效时才运行,而且主部件对备用部件有优先使用权和维修权;若在维修备用部件时主部件失效,则修理工立即停止修理备用部件,转入主部件修理.

假设7主部件运行失效维修时间X、主部件温贮备失效维修时间Y、备用部件失效维修时间U均服从一般连续分布,其分布函数分别为

假设8上述随机变量相互独立,当两个主部件与备用部件都发生故障时,系统故障和部件能修复如新.

假设9初始时刻两主部件与备用部件都是新的,主部件运行,另一主部件处于温储备状态,备用部件处于冷储备状态.

2 模型分析

定义1 S(t)表示系统在时刻t的状态,则系统在时刻t可能处于如下状态.

状态0:时刻t,系统主部件运行,另一主部件温贮备,备用部件冷贮备,系统正常.

状态1:时刻t,系统主部件运行,另一主部件温贮备失效维修,备用部件冷贮备,系统正常.

状态2:时刻t,系统主部件运行,另一主部件运行失效维修,备用部件冷贮备,系统正常.

状态3:时刻t,系统备用部件运行,主部件温贮备失效维修,另一主部件运行失效等待维修,系统正常.

状态4:时刻t,系统备用部件运行,主部件运行失效维修,另一主部件运行失效等待维修,系统正常.

状态5:时刻t,系统主部件温贮备失效维修,另一主部件运行失效等待维修,备用部件失效等待维修,系统失效.此状态时,在修理主部件之前备用部件还未开始修理.

状态6:时刻t,系统主部件温贮备失效维修,另一主部件运行失效等待维修,备用部件失效等待维修,系统失效.此状态时,在修理主部件之前备用部件已被修理过一段时间.

状态7:时刻t,系统主部件运行失效维修,另一主部件运行失效等待维修,备用部件失效等待维修,系统失效.此状态时,在修理主部件之前备用部件还未开始修理.

状态8:时刻t,系统主部件运行失效维修,另一主部件运行失效等待维修,备用部件失效等待维修,系统失效.此状态时,在修理主部件之前备用部件已被修理过一段时间.

状态9:时刻t,系统主部件运行,另一主部件运行失效维修,备用部件失效等待维修,系统正常.此状态时,在修理主部件之前备用部件还未开始修理.

状态10:时刻t,系统主部件运行,另一主部件运行失效维修,备用部件失效等待维修,系统正常.此状态时,在修理主部件之前备用部件已被修理过一段时间.

状态11:时刻t,系统主部件运行,另一主部件温贮备,备用部件失效维修,系统正常.

状态12:时刻t,系统主部件运行,另一主部件温贮备失效维修,备用部件失效等待维修,系统正常.此状态时,在修理主部件之前备用部件已被修理过一段时间.

系统的状态空间为Ω={0,1,2,3,4,5,6,7,8,9,10,11,12},其中系统的运行状态为W= {0,1,2,3,4,9,10,11,12},失效状态为F={5,6,7,8}.由于维修时间服从一般连续分布,则{S(t),t≥0}不是马尔可夫过程,为此我们引进补充变量

·X(t):当S(t)=2,4,7,8,9,10时,X(t)表示时刻t修理主部件运行失效已用去的时间.

·Y(t):当S(t)=1,3,5,6,12时,Y(t)表示时刻t修理主部件温贮备失效已用去的时间.

·U(t):当S(t)=6,8,10,11,12时,U(t)表示时刻t修理备用部件运行失效已用去的时间.则{S(t),X(t),Y(t),U(t),t≥0}构成一个广义马尔可夫过程,其状态空间为Ω*={0,［1,y］,［2,x］,［3,y］,［4,x］,［5,y］,［6,y,u］,［7,x］,［8,x,u］,［9,x］,［10,x,u］,［11,u］,［12,y,u］},其中x,y,u分别代表X(t),Y(t),U(t)的值.定义此广义马尔可夫过程的状态概率是

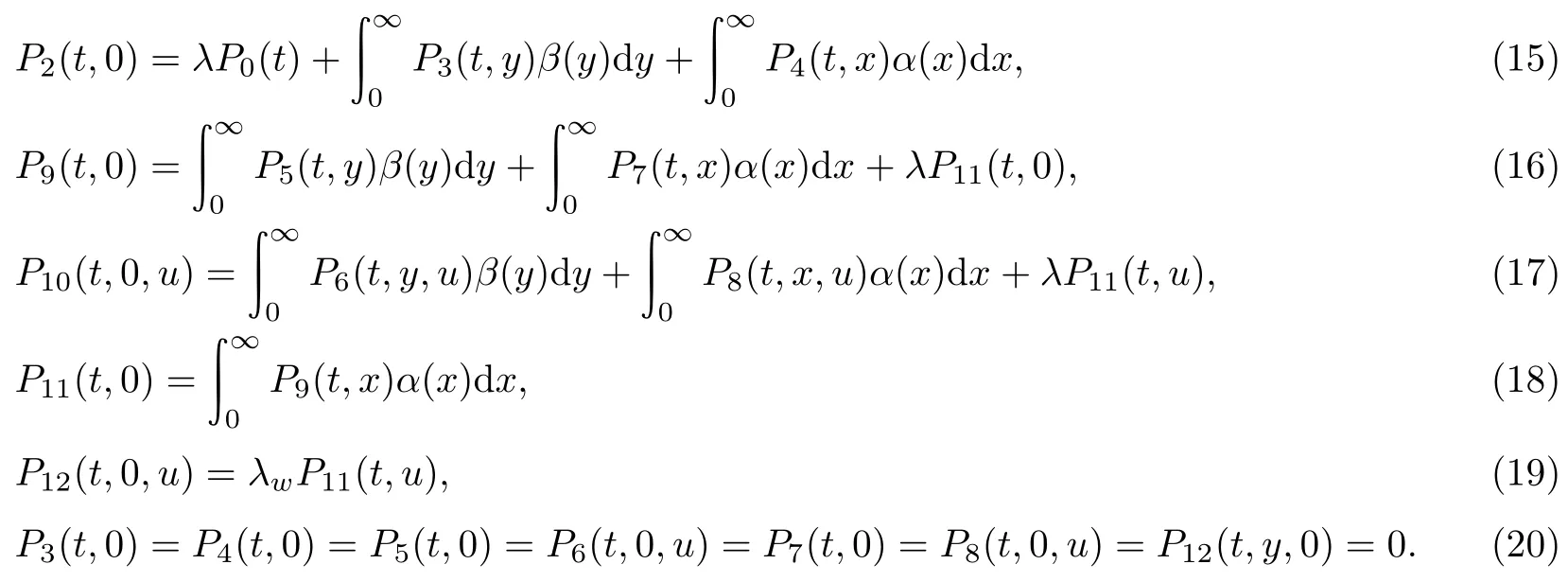
由总概率公式可得

(当i=1,3,5,6,12时m为y,当i=2,4,7,8,9,10时m为x,当i=11时m为u)初始条件为

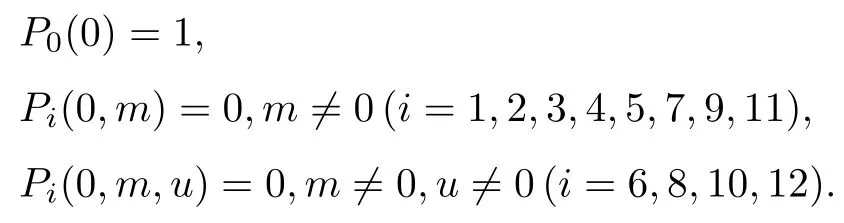
3 系统的稳态指标

定理1系统的稳态可用度为

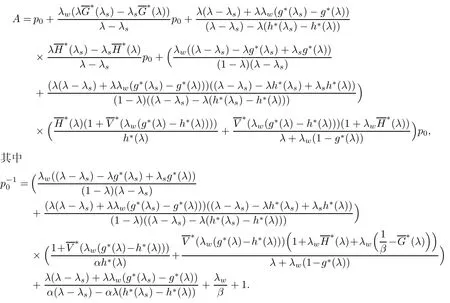
证明引入Lap lace变换表达式

根据系统正常工作时的稳态概率,可求得系统的稳态可用度为

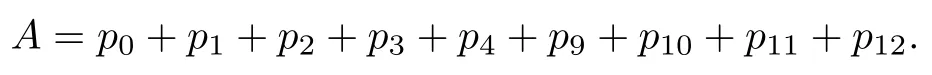
由此可得定理1.证毕.

定理2系统的稳态故障频度为

证明根据文献［11］中的计算方法,系统的稳态故障频度为

由定理1证明中已计算出的p3,p4,p9,p10,p12,代入上式即可得系统的稳态故障频度.证毕.

4 系统的可靠度与首次故障前的平均时间

定理3系统的可靠度R(t)的Lap lace变换式为

证明为求系统的可靠度R(t),只需将状态5与状态7看成是吸收状态,则状态6、状态8至状态12系统都无法达到.因此得到一个有吸收状态的、连续时间的、新的广义马尔可夫过程.令

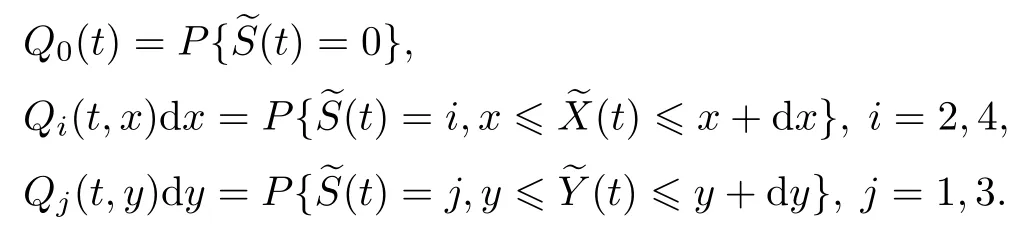
由此建立系统各状态概率的微分方程组

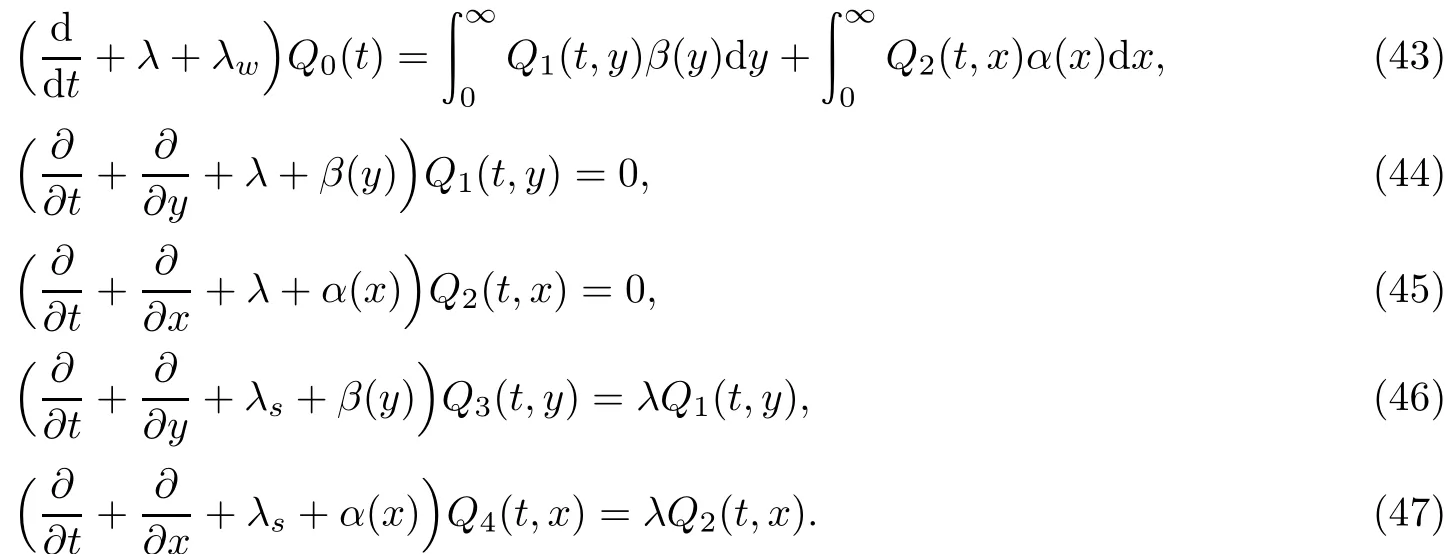
边界条件为

初始条件为

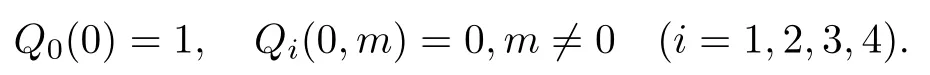
对方程(43)-(50)取Lap lace变换并结合初始条件可解得以上方程组

系统的可靠度为

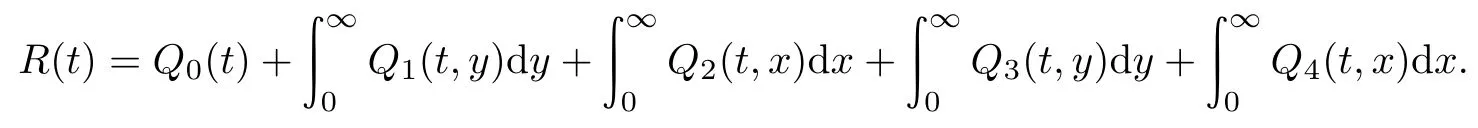
系统的可靠度R(t)的Laplace变换式为

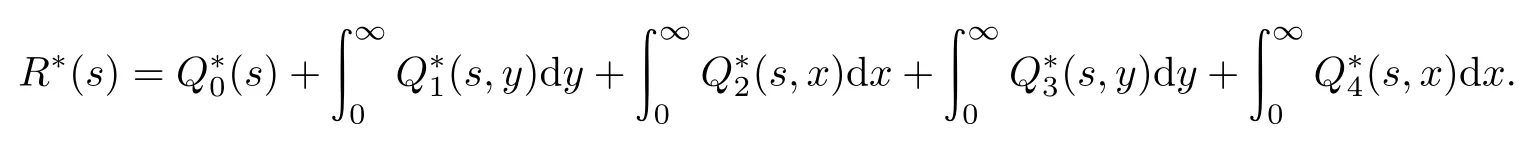
将我们已计算得的结果带入上式中即可得定理3.证毕.

推论1系统的首次故障前的平均时间

5 数值模拨分析

在这一节我们通过数值模拟来分析一些系统参数对系统可靠性的影响.

首先我们考虑温贮备失效率λw变化对系统可靠性的影响.假设部件的维修时间服从指数分布,令α(x)=0.7,β(y)=0.8,μ(u)=0.75,再令λ=0.3,λs=0.4.由于0＜λw＜λ,所以λw的取值范围为0.01-0.29.图1与图2分别描绘了系统稳态可用度A以及系统稳态故障频度M关于主部件温贮备失效率λw变化的曲线图.由图1与图2可以看出,系统稳态可用度A随着主部件温贮备的失效率λw增大而减小,系统稳态故障频度M随主部件温贮备的失效率λw增大而增大.

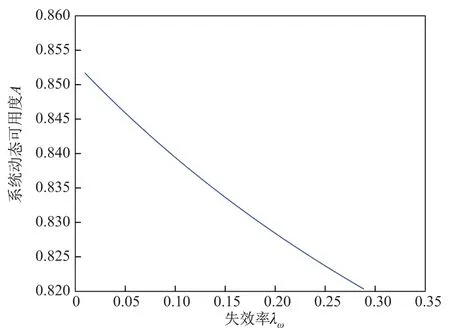
图1 系统稳态可用度A关于失效率λw而变化Fig.1 Steady-state availability of the system A With failure rateλwchanges

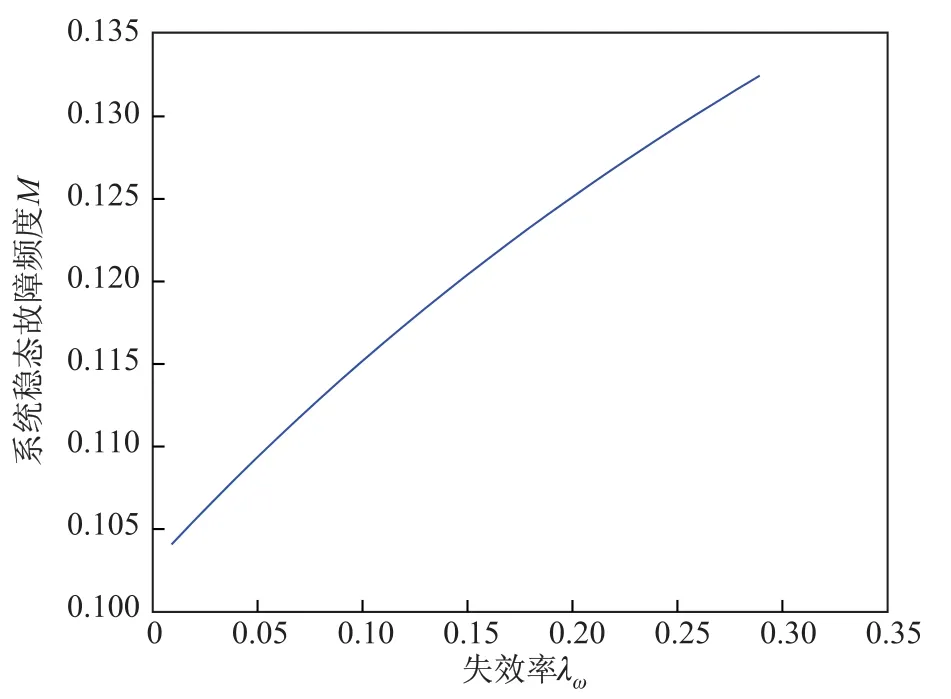
图2 系统稳态故障频度M关于失效率λw而变化Fig.2 Steady-state failure frequency of the system M With failure rateλwchanges

我们接着考虑主部件运行失效的修复率α(x)变化对系统可靠性的影响.同样假设部件的维修时间服从指数分布,令β(y)=0.9,μ(u)=0.7,再令λ=0.25,λw=0.15,λs=0.35. α(x)的取值范围为0.5-0.9.图3与图4分别描绘了系统稳态可用度A以及系统稳态故障频度M关于主部件运行失效的修复率α(x)变化的曲线图.由图3与图4可以看出,系统稳态可用度A随着主部件运行失效的修复率α(x)增大而增大,系统稳态故障频度M随主部件运行失效的修复率α(x)增大而减小.

6 结论

在实际情况中,增加贮备系统能大大提高系统的可靠性及安全性,而且贮备部件的无优先权可以节省系统开支,这从经济角度是有实际意义的.本文推导了Birolini双部件系统及一个无优先权的冷贮备备用部件组成的三部件可修系统的可靠性相关指标,并通过数值模拟比较分析了系统相关参数对系统可靠性指标的影响.

图3 系统稳态可用度A关于修复率α(χ)而变化Fig.3 Steady-state availability of the system A With repair rateα(χ)changes

图4 系统稳态故障频度M关于修复率α(χ)而变化Fig.4 Steady-state failure frequency of the system M With repair rateα(χ)changes

［1］吴清太,唐加山.泊松冲击下冷贮备可修系统的可靠性分析［J］.数理统计与管理,2012,31(1):149-156.

［2］刘宝友,方恢同.状态维修机械设备的可靠性和检测更换策略［J］.机械工程学报,2006(3):30-35.

［3］WANG H X, XU G Q. A cold system with two different components and a single vacation of the repairman ［J］.Applied Mathematics and Computation, 2012, 219: 2634-2657.

［4］WU Q, ZHANG J. A bivariate replacement policy for a cold standby system under poisson shocks ［J］. American Journal of Mathematical and Management Sciences, 2013, 32(3): 145-177.

［5］WU Q, WU S. Reliability analysis of two-unit cold standby repairable systems under poisson shocks ［J］. AppliedMathematics and Computation, 2011, 218: 171-182.[6］ WU Q.Reliability analysis of a cold standby system attacked by shocks[J］.Applied Mathematics and Computation,2012,218:11654-11673.

[7］ 岳德权,朱建玲.修理工可多重休假的带有一个冷贮备部件的Gaver并联系统[J］.系统工程理论与实践,2006 (6):59—68.

[8］ BIROLINI A.Reliability Engineering:Theory and Practice[M］.Berlin:Springer,2007.

[9］ ZHANG Y L,WANG G J.A deteriorating cold standby repairable system with priority in use[J］.European Journal of Operational Research,2007,183:278-295.

[10］ ZHANG Y L,WANG G J.A geometric process repair model for a repairable cold standby system with priority in use and repair[J］.Reliability Engineering and System Safety,2009,94:1782-1787.

[11］ 曹晋华,程侃.可靠性数学引论[M］.修订版.北京:高等教育出版社,2006.

(责任编辑 李 艺)

Reliability analysis of Birolini’s duplex system sustained by a non-priority unit in cold standby

HUANG Kai,WU Qing-tai
(College of Science,Nanjing Agricultural University,Nanjing 210095,China)

This paper deals With Birolini’s duplex system sustained by a non-priority unit in cold standby.It is assumed that the life of the unit is exponential distribution,and the repair time of the unit is general continuous distribution.Then by using supplementary variables approach and generalized Markov process method,the Lap lace transform of the reliability and the mean time to first failure are attained.Meanwhile,the availability and the failure frequency of the system are obtained.

priority rule;Birolini’s duplex system;reliability;generalized Markov process

O 213.2

A

10.3969/j.issn.1000-5641.2016.01.009

1000-5641(2016)01-0069-12

2014-12

中央高校基本科研业务费自主创新重点研究项目(KYZ201424)

黄凯,男,硕士研究生,研究方向为概率统计与可靠性分析.E-m ail:huangkai29@126.com.

吴清太,男,副教授,研究方向为系统可靠性分析与风险估计. E-mail:wuqingtai@njau.edu.cn.