一个参量化复合核Hilbert 型积分不等式

刘琼,黄琳

(1.邵阳学院理学与信息科学系,湖南邵阳422000; 2.长沙师范学院初等教育系,长沙410100)

一个参量化复合核Hilbert 型积分不等式

刘琼1,黄琳2

(1.邵阳学院理学与信息科学系,湖南邵阳422000; 2.长沙师范学院初等教育系,长沙410100)

通过引入一些特殊函数来刻画常数因子,获得一个核为ln(1+e-αχλ1yλ2)的Hardy-Hilbert型积分不等式,考虑了它的等价式,并证明了这对等价不等式的常数因子是最佳的.

Hilbert型积分不等式;权函数;最佳常数因子

0 引言

设θ(x)(＞0)是可测函数,ρ＞1,定义函数空间［1］:

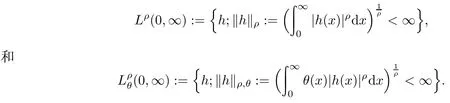
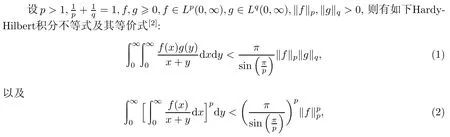
1 有关定义和引理

本文将用到以下特殊函数［12］:

2 主要结论

证明设置如下有界可测函数

上述不等式即为式(12),因此式(12)和式(14)等价.

若式(14)中的常数因子不是最佳的,则由式(14)得到式(12)的常数因子也不是最佳的,这与定理1已证过的结论矛盾,故常数因子是式(14)的最佳值.

我们在式(12)和式(14)中选取符合定理条件的参数α,λ1,λ2,以及共轭指数对(p,q)的合适值,可以得到一些有意义的不等式.

例1取λ1=λ2=1,p=q=2,由式(8),r=2,,则有下列等价不等式

致谢作者对审稿人提出的有益修改建议表示衷心感谢!

［1］程民德,邓东皋,龙瑞麟.实分析(第二版)［M］.北京:高等教育出版社,2008.

［2］HARDY G H, LITTLEWOOD J E, pOLYA G. Inequalities ［M］. Cambridge: Cambridge Univ press, 1952.

［3］MITRINOVIC D S, pECARC J E, FINK A M. Inequalities Involving Functions and Their Integrals and Derivatives［M］. Boston: Kluwer Academic publishers, 1991.

［4］杨必成,高明哲.关于Hardy-Hilbert不等式中的一个最佳常数［J］.数学进展,1997,26(2):159-164.

［5］洪勇.Hardy-Hilbert不等式的全方位推广［J］.数学学报,2001,44(4):619-626.

［6］杨必成.一个Hilbert型积分不等式［J］.浙江大学学报:理学版,2007,34(2):121-124.

［7］杨必成.一个非齐次核的Hilbert型积分不等式［J］.厦门大学学报:自科版,2009,48(2):165-169.

［8］刘琼,龙顺潮.一个核为双曲余割函数的Hilbert型积分不等式［J］.数学学报,2013,56(1):97-104.

［9］刘琼,杨必成.一个含多参数混合核的Hilbert型积分不等式及应用［J］.浙江大学学报:理学版.2012,39(2):135-141.

［10］杨必成.关于一个非齐次核的Hilbert型积分不等式［J］.上海大学学报:自科版,2011,17(5):603-606.

［11］刘琼.一个新的多参数Hilbert型积分不等式及其逆［J］.西南大学学报:自科版,2012,34(6):92-97.

［12］王竹溪,郭敦仁.特殊函数论［M］.北京:北京大学出版社,2000.

［13］匡继昌.实分析引论［M］.长沙:湖南教育出版社,1996.

［14］匡继昌.常用不等式［M］.济南:山东科学技术出版社,2004.

［15］王挽澜.建立不等式的方法［M］.哈尔滨:哈尔滨工业大学出版社,2011:334-377.

［16］杨必成.算子范数与Hilbert型不等式［M］,北京:科学出版社,2008.

(责任编辑林磊)

A Hilbert-type integral inequality With multi-parameters and composite kernel

LIU Qiong1,HUANG Lin2
(1.Department of Science and Information,Shaoyang University,Shaoyang Hunan 422000,China; 2.Department of Junior Education,Changsha Normal University,Changsha 410100,China)

By introducing some special functions to characterize the constant factor,a Hardy-Hilbert type integral inequality With the kernel ln(1+e-αχλ1yλ2)is obtained,and its equivalent form is considered.The constant factors of the equivalent inequalities are p roved being the best possible.

Hilbert-type integral inequality;weight function;the best constant factor

O178

A

10.3969/j.issn.1000-5641.2016.01.007

1000-5641(2016)01-0051-07

2014-12

国家自然科学基金(11171280);湖南省教育厅科学资助项目(10C1186)

刘琼,男,教授,研究方向为解析不等式、调和分析.E-mail:liuqiongxx13@163.com.

黄琳,女,副教授,研究方向为解析不等式、数学教育.E-mail:13787317290@163.com.