如何培养学生的数学思维

万丽娟

（进贤第六中学 江西南昌 331700）

如何培养学生的数学思维

万丽娟

（进贤第六中学 江西南昌 331700）

在数学教学中，如何开拓学生的思维，是教师直探索的教学课题。中学生学习数学有困难，其根源就在于学习数学过程中存在着不少的思维障碍。思维作为智力的核心，数学教学应围绕揭示思维过程，培养思维品质，发展学生思维能力为目的而展开。

学生思维 数学教学 培养

心理学认为，数学能力的差异，反映了数学思维品质的差异，初中学生的大脑已经接近成熟，思维能力有了比较显著的发展，因此，在初中数学教学中可以充分利用这一特点加强思维活动，使学生的智力得到更大的发展。下面是我在课堂教学中开拓学生思维的几点做法：

一、努力创设质疑，让学生主动进入思维活动

我国古代学者曾说过：“疑者，觉悟之机也，大疑则大悟，小疑则小悟，不疑则不悟”。因此，教师每讲授一节新知识，要根据教材要求和教学目标具体情况，创设质疑，使学生不自觉地产生一种强烈的求知欲望，激发学生主动进入思维活动。如教第三册几何《解直角三角几何《解直角三角形》这一课时，我设置了如下悬念，：“能否在不攀爬的条件下算出学校的旗杆的高度？”学生有的说能，有的说不能，气氛一下子活跃起来。我见学生的思维已调动起来，于是讲述了“解直角三角形”的一些实际应用。学生听起来都感到很惊奇，这样让学生带着悬念主动地学习新知识，收到了良好的教学效果。

二、变更角度，打破“思维定势”训练思维的灵活性

思维定势是人们长期形成的一种习惯性思维倾向，它让人以比较固定的思路去思考问题。当思维定势与问题的解答途径相一致时，思维定势起到积极的作用，当定势与解答途径不一致时，则产生消极影响，致使解答过程冗长烦琐，甚至半途而废。因此在教学中，应注意挖掘习题的内在潜力，启发学生灵活运用基本知识和技能，打破常规，克服思维定势，培养学生思维的灵活性。

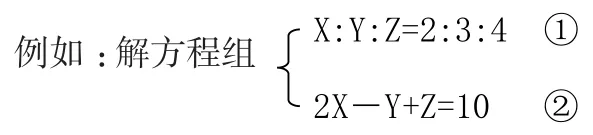
此题按常规解法：由①式导出三个比例式，再把其中两个与原方程组中②式联立为一个三元一次方程组，解这个三元一次方程组可得到原方程组的解。这样过程复杂、冗长。课堂上，我让学生仔细观察①式，有部分学生得到灵感，惊喜地发现由①式可得如果设则有把 X=2K，Y=3K，Z=4K代入原方程组的②式，便可求出K值，从而确定原方程组的解。

解：∵X：Y：Z＝2：3：4

∴设X＝2K，则Y＝3K，Z＝4K，代入②

得2×2K-3K＋4K＝10

解得K＝2

这种解法突破常规，更为简便，拓宽了思维领域，有效地训练了学生思维的灵活性。

三、指导学生广开思路，开拓学生思维的广阔性

思维的广阔性是指思维活动作用范围的广泛和全面程度。它表现为思路开阔，能全面地分析问题，多方向地思考问题，多角度地研究问题，善于对数学问题的特征、差异和隐含关系等进行具体分析，作出广泛的联想，能用各种不同的方法处理和解决问题。在教学中，对于同一个问题，教师应引导学生广开思路，多方向、多角度地进行思考，探求不同的解答方案，开拓思维的广阔性。

例：如图，已知⊙O1和⊙O2外切于P，AB切⊙O1于B，切⊙O2于A，求证：AB是两圆直径的比例中项。（选自《初中升学指导丛书》例题）

分析1.AB是两圆的外公切线，可利用求外公切线长的方法来证明。

证法一：如图（1）连结O2A，O1B，O1O2，则O1O2必过P点，O1B⊥AB，O2A⊥AB。

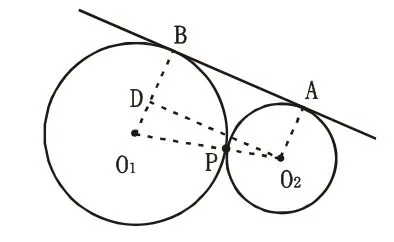
图（1）

作O2D⊥O1B于D，则O2D=AB，设O1B =R，O2A=r，R＞ r，

∴AB2=O2D2=O1O22- O1O2

2=（R+ r）2-（R- r）2=2R·2 r

∴AB是两圆直径的比例中项

分析2.易证△APB为直角三角形，延长BP交⊙O2于C点，延长AP交⊙O1于D点，则AC，BD就为两圆的直径，只要证等积式AB2=AC·BD成立就行了。

证法二：如图（2），连结AP并延长交圆于D点，连结BP并延长交圆于C点，连结AC，BD，过P点作两圆的公切线交AB于E点，则AE=PE=BE。

∴AP⊥BP，∠APC=∠BPD=90°

∴AC，BD为两圆直径

∵AB为两圆公切线

∴∠ABC=∠ADB，∠BAD=∠ACB

∴△ABC∽△BDA ∴ABBD =ACAB

∴AB2=AC·BD

即AB是两圆直径的比例中项。

开拓思维的广阔性是培养学生数学能力的重要环节。因此在教学中如何广开学生思路是值得每一位教师认真探讨的问题。

四、指导学生会归纳、总结、开拓学生思维的周密性

在教学中指导学生会对所学的知识进行归纳、总结，是开拓学生思维的又一途径，是学生对所学知识的一种本质认识，从而进一步巩固所学的知识。如一次函数Y=KX+b（k≠0）的图像的性质是一次函数教学的一个难点和重点，学生往往难以掌握，因此，我在课堂上讲完例题Y=2X+1，Y=-2X+1的图像后，即设置了几道填空题让学生练习。学生在填空过程中不但对旧的知识进行了复习，而且对新的知识有了更深的了解，对一次函数的图像性质有了系统归纳。在此后测试和模拟考试中学生很少做错此类题。

在平时，我们还会经常遇到一些题型结构不同，但用同一种方法解决的习题，对于这些问题如果教师在课堂上指导学生进行认真归纳和总结，学生一定会加深对问题的理解，以致达到牢固地掌握。

学生学会归纳、总结，是思维的一种升华，教师在教学中不要忽略这种思维的培养，要利用这种思维的周密性，开阔学生的视野。

总之，良好的思维品质应当包含多方面的内容，只要我们在教学工作中做到实处，有针对性地培养学生的积极思维，一定能收到较好的教学效果。